2000-10-10 - 2000-10-20
Leif Andersson
Henriksbergsvägen 104
136 67 HANINGE
Tel 08/777 45 33
e-post info@lexsup.se
Hemsida http://www.lexsup.se
GASERS EGENSKAPER
Allmänna gaslagen
Vad är värme?
---------------
Vår kunskap om vår omvärld bygger på den information vi får via våra sinnen.
Det ligger nära till hands att dela upp de förändringar som vi upplever efter de
sinnen som informerar oss om dem.Vi kallar det vi tar emot med ögonen för
ljus och det vi tar emot med öronen för ljud.I vår hud finns också sinnesorgan
som informerar oss om omgivningen.Bl a finns nerver som reagerar om hudens
molekyler ökar sin rörelsehastighet och det finns nerver som reagerar om
hudens molekyler minskar sin rörelsehastighet.Det som vi tar emot med dessa
organ kallar vi värme resp kyla.
Med en vass pennspets kan man studera detta organsystem.Vidrör huden,t ex
på handen baksida med spetsen.Om du råkar stöta mot en värmekännande
nerv känns spetsen varm,om du råkar stöta mot en nerv som känner av kyla
känns spetsen kall.Använder du en trubbig spets retar du samtidigt nerver
som känner värme,kyla och tryck.Resultatet blir då att du enbart upplever
tryckkänslan.
Vårt "värmesinne" känner alltså av hur hastigt molekylerna i huden rör sig.Och
det i sin tur beror på hur hastigt molekylerna i omgivande medium (luft eller,när
vi badar,vatten) rör sig och på hur mycket strålning som träffar huden och ger
hudmolekylerna rörelseenergi.
Eftersom vi alltså har ett värmesinne har vi i alla tider upplevt värme.Vi har
känt att en eld värmer och en isbit kyler.Men människor har undrat över vad det
var som gav dessa känslor.Man föreställde sig t ex att kemiska reaktioner avgav
någon sorts ämne som man kallade flogiston.Ett ämne som frisattes när bränslen
brann.Det var inte förrän för något århundrade sedan som vi förstod att det
handlade om molekylrörelser.
I fasta ämnen och i vätskor rör sig inte molekylerna fritt.De är bundna till
varandra med bindningskrafter som medför att det blir svårt att finna en
enkel beskrivning av deras rörelser.I en gas däremot är bindningskrafterna så
små att man kan föreställa sig gasmolekylerna som små fria kulor som far
omkring och kolliderar med varandra och med kärlväggar.Även om inte detta
stämmer exakt kan vi ju tänka oss en ideal gas d v s en gas där molekylerna
är oändligt små och helt utan bindningskrafter mellan sig.Om vi räknar på
hur en sådan gas skulle uppföra sig finner vi att vi kommer ganska nära en
beskrivning av hur vanliga gaser faktiskt uppför sig.Naturligtvis följer en
gas som är nära sin kondensationspunkt inte vad som gäller för en ideal gas
men för t ex vanlig torr luft är överensstämmelsen så god att vi kan dra
användbara slutsatser genom att räkna som om luften vore en ideal gas.
Om man tänker sig gasmolekylerna som oändligt små klotrunda partiklar kan
dessa ha hastighet och därmed rörelseenergi i tre av varnadra oberoende
rörelseriktningar.Vi säger att de har tre frihetsgrader.
Men de rör sig inte bara i olika riktningar,de stöter också mot varandra.
Och hur de stöter emot varandra påverkar också hur mycket energi de har.Ju
oftare och ju häftigare de kolliderar ju mer energi omsätts vid kollisionerna.
Genom att kollidera med kärlväggar och omgivande molekyler håller en molekyl
upp en volym runt sig och häftigheten i kollisionerna med kärlväggarna
uppfattar vi som ett gastryck.När man räknar på gasers beteende finner man
att varje molekyl skall tilldelas två frihetsgrader som motsvarar dess
bidrag till hela gasens tryck och volym.Vi får alltså sammanlagt fem
frihetsgrader tre knutna till molekylhastighet i tre riktningar och
två knutna till hela gasens tryck och volym.Vi kan säga att vi har tre
inre och två yttre frihetsgrader.
Om vi innesluter en gas som praktiskt taget uppför sig som en ideal gas i
en cylinder med kolv kan vi värma gasen och låta kolven röra sig utåt så
att volymen ökar men trycket hålls konstant.När kolven rör sig utåt uträttar
den ett arbete som vi kan ta vara på t ex för att pumpa vatten ur en gruva.
Vi finner nu att kvoten mellan tillfört värme och temperaturökningen hela
tiden blir konstant.Vi kan kalla denna kvot för Cp.
Så gör vi om samma sak men låter kolven sitta fast så att trycket stiger
vid konstant volym.Nu uträttar inte kolven något arbete.Även nu finner vi
att kvoten mellan tillfört arbete och temperaturökningen blir konstant men
konstanten får ett annat värde än förra gången.Vi kallar detta nya värde
för Cv.
Om vi använde en enatomig ädelgas blev förhållandet Cp/Cv = 1,67.
Varför?
I andra fallet fördelades all tillförd värmeenergi på de tre inre frihets-
graderna.Om vi tolkar temperaturen som ett mått på energin per frihets-
grad skall vi alltså tillföra tre gången så mycket energi som vad som
hanmar på varje frihetsgrad. Cv blir 3 (J/molekyl)/(J/frihetsgrad).
I första fallet däremot måste vi förutom att tillföra energi till de tre inre
frihetsgraderna även tillföra energi till de två yttre.Att vi håller konstant
tryck innebär att vi tillför lika mycket till varje frihetsgrad.Det värme
som vi tillför fördelas alltså på fem frihetsgrader.Vi måste tillföra
fem gånger så mycket energi som vad som hamnar på varje frihetsgrad.
Cp blir 5 (J/molekyl)/(J/frihetsgrad).
Vi får alltså Cp/Cv = 5/3 = 1,67.
Nu mäter vi inte temperatur i J/frihetsgrad utan i Kelvin som är
1 K = k/2 = 0.69 10-23 J/frihetsgrad (k = Boltzmanns konstant)
men det innebär bara en del trassel med sortomvandling.Och ofta anges
Cp och Cv inte för ett visst antal molekyler utan t ex för 1 kg
gas vilket innebär att värdena påverkas av molekylvikten.Både sort-
omvandling för temperaturenheten och molekylvikten går emellertid att
förkorta bort när man tar Cp/Cv och resultatet blir därför
alltid 1,67 om man använder samma ädelgas vid båda mätningarna.
Om man tar en tvåatomig gas tillkommer en möjlighet för molekylerna att
bära energi.Molekylerna ser då ut som små stavar och dessa kan inte bara
röra sig i tre oberoende riktningar,de kan även rotera.Förutom translation
i tre riktningar kan de även rotera kring tre av varandra oberoende axlar.
För tvåatomiga gaser bortfaller rotationen kring molekylernas längsaxel
(ett intressant fenomen som är värt sin egen mässa).Tvåatomiga gaser får
därför tre translationsfrihetsgrader och två rotationsfrihetsgrader.
Därtill kommer som för enatomiga gaser två yttre frihetsgrader.
För tvåatomiga gaser blir alltså Cp blir 7 (J/molekyl)/(J/frihetsgrad)
och Cv blir 5 (J/molekyl)/(J/frihetsgrad).
Vi får alltså Cp/Cv = 7/5 = 1,4.
Och för treatomiga gaser får vi tre translationsfrihetsgrader,tre
rotationsfrihetsgrader och två yttre frihetsgrader.
Vi får alltså Cp/Cv = 8/6 = 1,33.
Och när man mäter på verkliga gaser som har små molekyler och ligger långt
från kondensation finner man att dessa värden ligger nära de mätresultat
man då får.
Antag att man har en cylinder med kolv.Så skjuter man in kolven så att den
inneslutna volymen blir noll.Om man nu håller emot så att det krävs ett
visst tryck för att pressa ut den och pumpar in gas så att den pressas ut
kommer gasen att uträtta ett arbete.Det arbete som gasen har uträttat är
trycket (P) gånger gasvolymen (V).
Till detta yttre arbete (PV) är två frihetsgrader per molekyl knutna.Vi har
då
PV = 2 N T
där
2 anger att det är fråga om två frihetsgrader
N = antalet molekyler i gasen
T = energi per frihetsgrad
Avogadros lag säger
Lika volymer av olika gaser innehåller,vid samma tryck och temperatur,
lika många molekyler
Det innebär att en mol av en gas innehåller lika många molekyler oavsett
vilken gas det är (gäller för gaser som beter sig som ideala gaser).För
1 kmol är
N = 6,02 1026 (Avogadros tal)
Om vi dessutom anger T i Kelvin i stället för i J/frihetsgrad får vi för
1 kmol
PV = 2 (k/2) N T = R T
där
R = 2 (k/2) N = k N = 8314 J/(kmol K) (Allmänna gaskonstanten)
För en gas med massan m kg och molekylvikten M gäller alltså
PV = (m/M) R T (Allmänna gaslagen)
När man räknar på tillståndsförändringar för gaser med hjälp av Allmänna
gaslagen hanterar man alltså tre storheter
Tryck P
Volym V
Temperatur T
Ofta underlättar man beräkningarna genom att studera fall där någon
storhet hålls konstant.De vanligaste fallen är
Isobar Konstant tryck
Isokor (Isochor) Konstant volym (Inget arbete avges)
Isoterm Konstant temperatur
Adiabat (Isentrop) Inget värme avges
En tillståndsförändring där ingen storhet hålls konstant kallas Polytrop.
För att hämta ett program som du kan använda för beräkning av tillstånds-
förändringar enligt allmänna gaslagen klickar du på nedanstående rubrik
Programmet beräknar tillståndsförändring för en innesluten gasmängd.Ofta
vill man genomföra förändringar i flera steg och det skulle då vara bra
om man kunde addera flera steg till ett totalt resultat.Men problemet
är att man kan göra sådana flerstegsoperationer på olika sätt och jag
har funnit att det bästa sättet faktiskt är att addera dem med papper
och penna så att man får ihop resultatet på det sätt man vill.Programmet
kan då användas för beräkning av varje steg.
Observera också att programmet bara räknar på vad som händer med den
inneslutna gasmassan.Om du t ex skjuter in en kolv får du hjälp av
atmosfärstrycket.För att få det arbete du behöver lägga ner skall du
då dra atmosfärsarbetet (volymändringen gånger atmosfärstrycket) från
det beräknade arbetet.Detta gör inte programmet.
Om du t ex skall pumpa ett däck måste du komprimera luft i pumpen så
att du kommer upp till däcktrycket.Hur mycket som åtgår för detta kan
du beräkna med programmet.Genom att dra bort atmosfärsarbetet får du
då reda på hur mycket arbete du måste tillföra för att komma upp till
däcktryck.Men sedan måste du trycka in den komprimerade luften i
däcket.För det krävs ett fulltrycksarbete som är den komprimerade
luftens volym gånger däcktrycket.Och även här drar du bort atmosfärs-
arbetet (den komprimerade luftens volym gånger atmosfärstrycket) för
att få veta vad du måste tillföra.Inte heller sådana beräkningar av
fulltrycksarbete gör programmet.
På min dator händer ibland att siffran i en färgad ruta inte försvinner
när man klickar på den.Klicka i så fall en gång till (ej dubbelklick).
Beräkningar enligt Polytrop fungerar (hoppas jag) men man får se upp
med angivna slutvärden.De kan innebära orimliga beräkningsvärden på
vägen som får programmet att krascha.
Jag har satt ihop programmet av bitar av ett gammalt program.Hoppas allt
blev rätt.Hör av dig om du upptäcker något fel!
Värme är alltså slumpmässig rörelseenergi hos molekyler.Energi per
frihetsgrad kallas för temperatur och antalet frihetsgrader kallas
för entropi.
Temperatur är värmelärans intensitetsbegrepp och entropi är värmelärans
mängdbegrepp.Motsvarande begrepp för värmelära och ellära är
Värmelära Ellära
Temperatur Potential
Temperaturskillnad Spänning
Entropi Laddning
Frihetsgrad Elektron
För en viss mängd av en ideal gas är entropin alltid konstant.
Men om vi t ex komprimerar en ideal gas isotermt tillför vi arbete till
gasen via ändring av PV och detta arbete avges till omgivningen i form av
värme.Det tillförda arbetet fördelas alltså ut som värme på frihetsgrader
i omgivningen.Vi säger att entropin ökar när arbete blir värme och denna
entropiökning är alltså frihetsgrader i omgivningen.Om vi t ex håller
konstant temperatur genom att kyla med smältande is ökar entropin i
omgivningen genom att vattenmolekyler får fler frihetsgrader när de kan
röra sig i vätska i stället för i is.
Om PV-diagrammet
----------------
Allmänna gaslagen innehåller tre variabler (tryck (P) , volym (V) och
temperatur (T)).För att beskriva tillståndsförändringar kan vi då använda
ett tredimensionellt diagram med tryck,volym och temperatur avsatta
efter axlarna.
Men att rita tradimensionella diagram är besvärligt och ofta använder vi
i stället projektioner på tvådimensionella diagram.
Om vi är intresserade av hur mycket arbete som omsätts vid en viss till-
ståndsförändring är det lämpligt att använda en projektion på ett PV-
diagram.En gas utbyter ju arbete med omgivningen via PV-termen.
Hur en gas uppför sig i PV-diagrammet under en viss tillståndsförändring
beror på hur vi tillför eller bortför värme under tillståndsförändringen.
Om vi t ex håller temperaturen konstant får vi ett samband mellan P och V
som ungefär ser ut som i fig 1
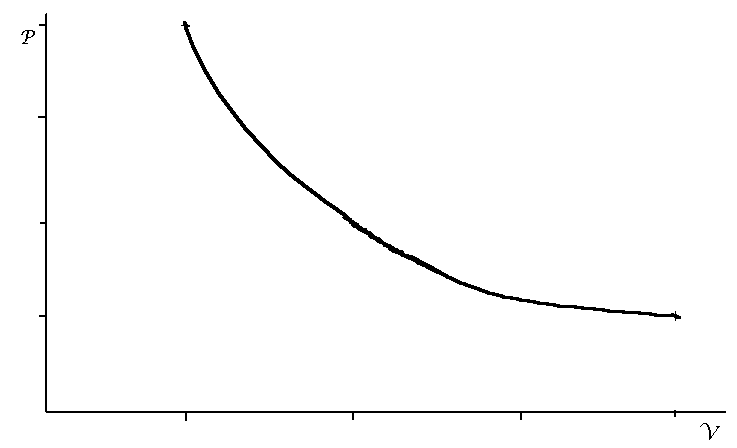 Fig 1
Om vi innesluter volymen V1 vid atmosfärstrycket P1 och komprimerar
till volymen V2 vid trycket P2 åtgår ett arbete som motsvarar
den blå ytan i fig 2
Fig 1
Om vi innesluter volymen V1 vid atmosfärstrycket P1 och komprimerar
till volymen V2 vid trycket P2 åtgår ett arbete som motsvarar
den blå ytan i fig 2
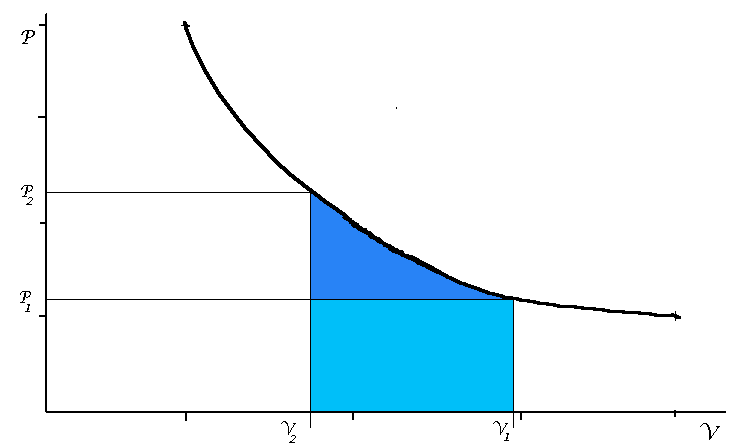 Fig 2
Den ljusblå delen av detta arbete är atmosfärsarbetet d v s det arbete som
atmosfären bidrar med och den mörkblå delen är det arbete som vi måste
tillföra.
Men vi kan komma från utgångsläget P1 V1 till slutläget P2 V2
på många sätt.Vi kan t ex minska V från V1 till V2 genom att kyla
gasen vid konstant tryck.Vi får då en isobar enligt den röda linjen i fig 3.
Så kan vi öka trycket från P1 till P2 genom att värma vid konstant volym.
vi får då en isokor enligt den grå linjen i fig 3.Det arbete som tillförs vid
isobaren är enbart atmosfärsarbetet och arbetet vid isokoren är noll.Vi behöver
alltså i detta fall inte tillföra något arbete.Vi har tagit oss från utgångsläge
till slutläge enbart genaom att bortföra och tillföra värme.
Fig 2
Den ljusblå delen av detta arbete är atmosfärsarbetet d v s det arbete som
atmosfären bidrar med och den mörkblå delen är det arbete som vi måste
tillföra.
Men vi kan komma från utgångsläget P1 V1 till slutläget P2 V2
på många sätt.Vi kan t ex minska V från V1 till V2 genom att kyla
gasen vid konstant tryck.Vi får då en isobar enligt den röda linjen i fig 3.
Så kan vi öka trycket från P1 till P2 genom att värma vid konstant volym.
vi får då en isokor enligt den grå linjen i fig 3.Det arbete som tillförs vid
isobaren är enbart atmosfärsarbetet och arbetet vid isokoren är noll.Vi behöver
alltså i detta fall inte tillföra något arbete.Vi har tagit oss från utgångsläge
till slutläge enbart genaom att bortföra och tillföra värme.
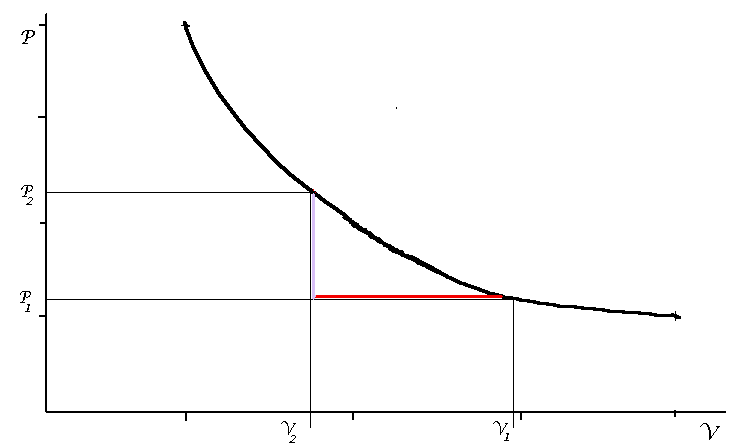 Fig 3
Om vi vill veta hur mycket arbete som krävs för att komma från ett tillstånd
till ett annat räcker det alltså inte att veta de två tillståndens tryck,volym
och temperatur.Man måste också veta vilken väg man går mellan dem.
Detta vållar bl a problem när man vill räkna på tillståndsförändringar för
fuktig luft.Genom att vatten kan kondensera och förångas med avgivning eller
upptagning av värme blir det svårt att beskriva hur man egentligen går mellan
start- och sluttillstånd.Speciellt som de flesta processer går så snabbt att
kondensationsprocessen inte hinner nå jämvikt under förändringen.
___________________________________
-----------------------
Fig 3
Om vi vill veta hur mycket arbete som krävs för att komma från ett tillstånd
till ett annat räcker det alltså inte att veta de två tillståndens tryck,volym
och temperatur.Man måste också veta vilken väg man går mellan dem.
Detta vållar bl a problem när man vill räkna på tillståndsförändringar för
fuktig luft.Genom att vatten kan kondensera och förångas med avgivning eller
upptagning av värme blir det svårt att beskriva hur man egentligen går mellan
start- och sluttillstånd.Speciellt som de flesta processer går så snabbt att
kondensationsprocessen inte hinner nå jämvikt under förändringen.
___________________________________
-----------------------
 Fig 1
Om vi innesluter volymen V1 vid atmosfärstrycket P1 och komprimerar
till volymen V2 vid trycket P2 åtgår ett arbete som motsvarar
den blå ytan i fig 2
Fig 1
Om vi innesluter volymen V1 vid atmosfärstrycket P1 och komprimerar
till volymen V2 vid trycket P2 åtgår ett arbete som motsvarar
den blå ytan i fig 2
 Fig 2
Den ljusblå delen av detta arbete är atmosfärsarbetet d v s det arbete som
atmosfären bidrar med och den mörkblå delen är det arbete som vi måste
tillföra.
Men vi kan komma från utgångsläget P1 V1 till slutläget P2 V2
på många sätt.Vi kan t ex minska V från V1 till V2 genom att kyla
gasen vid konstant tryck.Vi får då en isobar enligt den röda linjen i fig 3.
Så kan vi öka trycket från P1 till P2 genom att värma vid konstant volym.
vi får då en isokor enligt den grå linjen i fig 3.Det arbete som tillförs vid
isobaren är enbart atmosfärsarbetet och arbetet vid isokoren är noll.Vi behöver
alltså i detta fall inte tillföra något arbete.Vi har tagit oss från utgångsläge
till slutläge enbart genaom att bortföra och tillföra värme.
Fig 2
Den ljusblå delen av detta arbete är atmosfärsarbetet d v s det arbete som
atmosfären bidrar med och den mörkblå delen är det arbete som vi måste
tillföra.
Men vi kan komma från utgångsläget P1 V1 till slutläget P2 V2
på många sätt.Vi kan t ex minska V från V1 till V2 genom att kyla
gasen vid konstant tryck.Vi får då en isobar enligt den röda linjen i fig 3.
Så kan vi öka trycket från P1 till P2 genom att värma vid konstant volym.
vi får då en isokor enligt den grå linjen i fig 3.Det arbete som tillförs vid
isobaren är enbart atmosfärsarbetet och arbetet vid isokoren är noll.Vi behöver
alltså i detta fall inte tillföra något arbete.Vi har tagit oss från utgångsläge
till slutläge enbart genaom att bortföra och tillföra värme.
 Fig 3
Om vi vill veta hur mycket arbete som krävs för att komma från ett tillstånd
till ett annat räcker det alltså inte att veta de två tillståndens tryck,volym
och temperatur.Man måste också veta vilken väg man går mellan dem.
Detta vållar bl a problem när man vill räkna på tillståndsförändringar för
fuktig luft.Genom att vatten kan kondensera och förångas med avgivning eller
upptagning av värme blir det svårt att beskriva hur man egentligen går mellan
start- och sluttillstånd.Speciellt som de flesta processer går så snabbt att
kondensationsprocessen inte hinner nå jämvikt under förändringen.
___________________________________
-----------------------
Fig 3
Om vi vill veta hur mycket arbete som krävs för att komma från ett tillstånd
till ett annat räcker det alltså inte att veta de två tillståndens tryck,volym
och temperatur.Man måste också veta vilken väg man går mellan dem.
Detta vållar bl a problem när man vill räkna på tillståndsförändringar för
fuktig luft.Genom att vatten kan kondensera och förångas med avgivning eller
upptagning av värme blir det svårt att beskriva hur man egentligen går mellan
start- och sluttillstånd.Speciellt som de flesta processer går så snabbt att
kondensationsprocessen inte hinner nå jämvikt under förändringen.
___________________________________
-----------------------