Leif Andersson
Henriksbergsvägen 104
136 67 HANINGE
Tel 08/777 45 33
e-post leif.andersson@haninge.mail.telia.com
Hemsida http://lexsup.se
Denna text kan du ladda ner som zip-fil genom att klicka på Ägarhandbok
2004 med viss bearbetning 2010
V Ä R L D E N
Ägarens handbok
Innehåll:
FÖRORD
DEL 1
Inledning
Välbefinnande
Livsprojekt - Livsmening
Bäst i världen
Inte sämst
Stödja andra
Fabulöst rik
Omtyckt av dina närmaste
Hatobjekt
Förstå hur världen fungerar
Översätta världens språk till och från mänskligt
Långsiktig uppgift
Reglage och styrmedel
Orsak och verkan
Servon
Religion
Ekonomi
Fysik
Adresserbara ventiler
Inte bara förändring
Garantivillkor och varningstext
DEL 2
Vad är teknik?
Vår villiga värld
Om att slå och kasta
Teknikens grundstenar
Koordinater
Vad är energi
Vad är tid
Vad vill vi egentligen?
Hastighet
Parametertid och koordinattid
Rörelseenergi
Intuition
Stabilitet
DEL 3
Hur fungerar världen?
Vad är verklighet?
Plancks konstant - Alltets konstant
Bortom tid och rum
Tid
Rum
Orsak och verkan
Energi
Arbete
Kraft
Brus
Den fyrdimensionella världen
Gravitation
Liv
Olika energiformer
Mängdändring
Transformatorn och väduren
Om sorter
Måttsystem
DEL 4
Etervinden
Högsta möjliga hastighet
Vad är mönster?
Vad är potential?
Vad är absolut nollpunkt?
Absolut nollpunkt för lägesenergi
Elementarpartiklar - små svarta hål
Vad är frihetsgrad?
Den olinjära etern
Brahma,samsara,karma
Oändlighet
Ekonomi
Karmamarga eller jnanamarga
APPENDIX
Laplacetransformen - Differentialkalkylens 'logaritm'
Vektoranalys
Tensorkalkyl
FÖRORD
En mycket kortfattad beskrivning av världen är enkel. Världen är lika med h.
Men om vi vill ha med lite fler detaljer blir det knepigare. Vad skall man
ta med och vilken utgångspunkt skall man välja?
Jag har valt att använda fyra olika utgångspunkter och dela upp materialet i
fyra av varandra oberoende delar. Det innebär visserligen en del upprepningar
eftersom samma synpunkter blir aktuella från olika utgångspunkter men jag
tror att det kan vara motiverat att ibland se samma sak ur olika vinklar.
I del 1 har jag som utgångspunkt använt den typ av välmenande råd som en
tillverkare (Skapare) skulle kunna tänkas försöka förmedla till kunden i sin
naiva tro att kunden börjar med att läsa handboken.
I del 2 har jag utgått från hur vår tekniska kunskap har vuxit fram.
Del 3 är ett försök att beskriva hur världen fungerar.
Del 4 är också ett försök att beskriva hur världen fungerar men denna del
skiljer sig från del 3 genom att den innehåller synsätt som är mer hypotetiska.
Slutligen finns i ett appendix lite om några matematiska verktyg.
Denna ägarhandbok tar endast upp användning av död materia. Användning av
levande varelser kommer att behandlas i en planerad handbok för samhällsägare.
Och alltsammans bygger på mitt sätt att se världen. Denna världsbild kan
naturligtvis ifrågasättas och diskuteras. Gör det!!! Putsa upp din egen
världsbild och dela med dig av den.
Varje människa är en skrattspegel som speglar verkligheten till en
världsbild. Ingen av oss har en plan spegel men alla bilder har intressanta
drag.
DEL 1
Inledning
=========
Tack för att du valde den här världen!
Om du använder den här världen på lämpligt sätt kommer den att ge
dig ett sekel fyllt med intressanta upplevelser. Men "intressanta
upplevelser" är inte ett sekellångt lyckorus. Även besvikelse, skräck,
sorg, ilska och förtvivlan är "intressanta upplevelser" som är
nödvändiga som kontrast till lyckokänslor. Och världen är en
komplicerad produkt som kräver en del av sin ägare för att ge en
bra blandning av olika slags upplevelser.
Bortsett från vissa, föga intressanta, logiska motsägelser, t ex
enhandsapplåder, varmkall soppa och vakumljud, tillfredsställer
världen alla dina önskemål - om du uttrycker dem på ett språk
som världen "förstår". Problemet är inte att världen inte gör som
du ber den, problemet är att den gör nästan exakt som du ber den. Ett
tydligt exempel på detta är den lilla del av världen som en dator
utgör. Om du skriver ett program där du talar om för datorn vad den
skall göra finner du ofta att den inte gör vad du hade tänkt dig.
Men felet är mycket sällan att datorn inte följer programmet. Felet
är att den gör exakt vad som står i programmet och när du analyserar
programmet närmare inser du att det är datorn som tolkar programmet
korrekt. Den, liksom resten av världen, har ingen "överseendefunktion",
ingen funktion som synar ditt program och konstaterar att: "Så kan
han väl ändå inte mena! Det måste vara så här han menar! Jag gör så i
stället." Och var glad för det! Problemen med att programmera en
dator som gör exakt vad man ber om är ett intet i jämförelse med
problemen att hantera en "användarvänlig" dator som försöker rätta
till programfel.
Det finns en historia om den duktige skogshuggaren som fällde hundra
träd per dag. En gång var han inne hos järnhandlaren som sa: "Du borde
köpa en motorsåg så skulle du kunna fälla ännu fler träd". Det lät ju
bra så han köpte en men efter en vecka kom han tillbaka och sa: "Det
går inte. Hur jag än sliter kommer jag inte upp i mer än hundra träd
per dag". "Kan det vara något fel på den" sa handlarn och drog igång
den. "Å fan!!" sa skogshuggaren "Surrar den?".
Du äger naturligtvis din värld men för att få fullt utbyte av den
behöver du veta hur du får den att surra.
Även om du äger en flaska nitroglycerin och får göra vad du vill med
den har du anledning att ta det försiktigt. Med lämplig hantering är
den ett mycket kraftfullt hjälpmedel för att förverkliga dina önskemål,
med olämplig hantering kan den utplåna hela din värld.Och en flaska
nitroglycerin är bara en liten, liten del av världen.
TÄNK PÅ DITT ÄGARANSVAR!
Även om du äger en bil bör du inte köra över andras trädgårdar.
Även om du äger en motorgräsklippare och en gräsmatta bör
du inte klippa gräsmattan mitt i natten när andra vill sova.
Även om du äger din värld bör du inte försvåra för andra när
de vill använda sina världar.
Välbefinnande
=============
Kroppen har ett "belöningssystem" som kan frisätta morfinliknande
belöningssubstanser. Dessa belöningssubstanser stimulerar välbefinnande-
receptorer. Välbefinnandereceptorerna kan liknas vid R-S-vippor.De
kan alltså betraktas som komponenter med egenskapen att de har två
stabila lägen som vi kan kalla för"Reset" och "Set".
Belöningssubstanserna driver välbefinnandereceptorerna i läge
"Set" . Övergången från "Reset" till "Set" upplever vi som en
välbefinnandekänsla. Det är alltså den skur av pulser som avges
när ett antal välbefinnandereceptorer slår om från "Reset" till
"Set" som ger välbefinnandekänsla medan välbefinnandereceptorer
som befinner sig stabilt i läge "Set" inte ger någon välbefinnande-
känsla. Om en viss receptor övergått från "Reset" till "Set" och
givit ett bidrag till välbefinnandekänslan måste vi alltså genomföra
en reset d v s återställa den i läge "Reset" för att den på nytt
skall kunna bidra till välbefinnandekänslan.
När välbefinnandereceptorerna övergår från "Set" till "Reset"
upplever vi en känsla av oro och ångest. Men denna känsla är nödvändig
för att vi skall kunna uppleva välbefinnande. Om vi enbart stimulerar
receptorerna att övergå till läge "Set" kommer förr eller senare alla
receptorer att befinna sig i läge "Set" så att ingen välbefinnandekänsla
blir möjlig om man inte gör reset. När du känner dig deppig och nere
förbereder du alltså kommande välbefinnandekänsla genom att göra reset.
Med hjälp av narkotika t ex morfin kan man stimulera välbefinnande-
receptorerna att slå om från "Reset" till "Set" och ge en välbefinnande-
känsla. Förr eller senare måste man emellertid genomföra reset om man
skall kunna återanvända receptorerna. Med narkotika kan man alltså
åstadkomma övergång från "Reset" till "Set". Att åstadkomma denna övergång
är emellertid knappast något problem. Det finns en rad andra metoder för
detta.Problemet är att göra reset på ett acceptabelt sätt. Med narkotika
löser man alltså inget problem men man försvårar problemet att göra reset
genom att man driver över så stort antal receptorer i läge "Set" att man
måste genomföra en mycket omfattande reset. Man kan också få problemet
att man försöker göra reset vid relativt hög halt av naturliga eller
syntetiska belöningssubstanser vilket leder till att reset-operationen
misslyckas. Receptorer övergår från "Set" till "Reset" och ger oro och
ångest samtidigt som andra receptorer återgår till "Set" och ger väl-
befinnandekänsla (s k snedtändning).
Resetkänslan anses obehaglig och det har därför utvecklats en mängd
metoder att dämpa upplevelsen av reset. Alla religioner innehåller en
mängd anvisningar hur man kan göra reset. När vissa religioner stadgar
att man skall känna sig usel och syndfull ligger i den påbjudna oron
över uselheten en reset. Genom att denna påbjuds av religionen och
genom att den är svår att uppnå ger själva oron även upphov till
frisättande av belöningssubstans. Man skall alltså oroa sig över sin
syndfullhet tills man gjort en omfattande reset. Därefter skall man
konstatera att man lyckats uppfylla religionens bud vilket medför
att belöningssubstans frisätts och en del av de receptorer som gått
i läge "Reset" återgår i läge "Set". Genom att detta inträffar först
sedan man slutat göra reset upplever man en ren välbefinnandekänsla.
Ett vanligt sätt att maskera reset-känslan är att koncentrera
uppmärksamheten på någon annan samtidig upplevelse. Man kan givetvis
inte maskera reset-känsla genom att stimulera välbefinnandereceptorer
att gå över i läge "Set". Men man kan utnyttja en rad andra känslor
som inte har samband med välbefinnandereceptorerna.
I vårt samhälle finns en lång tradition att maskera reset-känsla med
ambition. Vi sätter upp ett mål som är så svårt att nå att vi vet att
det kräver koncentration. Så koncentrerar vi oss på uppgiften och
genomför en reset.Att denna metod blivit mycket använd sammanhänger
med att oväntad ambitionsuppfyllelse är det kanske allra effektivaste
sättet att utlösa frisättning av belöningssubstans.
I bl a österländska religioner används ofta metoden att koncentrera
uppmärksamheten mot ett abstrakt gudsbegrepp i stället för mot en
konkret uppgift. Syftet är att nå en fullständig reset där alla
receptorer befinner sig i läge "Reset" och alltså inte kan orsaka
ångest genom att övergå från "Set" till "Reset".
Din kropp är en del av din värld.Även om du äger den liksom resten av
världen och gör vad du vill med den bör du ta reda på hur den fungerar
innan du börjar manipulera den. Du kan nå kroppens belöningssystem
via ett antal, mer eller mindre väl utprovade, program. Och du kan
också komma åt belöningssystemet direkt på hårdvarunivå med hjälp av
droger men som det brukar stå i datamanualerna: "Vi avråder på det
bestämdaste för manipulationer på denna låga nivå såvida du inte är
absolut säker på att du vet vad du gör."
Livsprojekt - Livsmening
========================
Vad skall du ha världen till? Vad vill du göra med den?
Enligt judisk tradition skapade Jahve världen ofullkomlig för att
människan skulle ha en uppgift med att fullkomna den.Hur ser din
vision av en fullkomlig värld ut?
Vi har en del medfödda önskemål som gör att vi tillgodoser våra
fysiologiska behov. Alla som någon gång hamnat i en situation där
vår fysiologiska överlevnad hotats vet hur snabbt civilisationsfernissan
krakelerar, hur vi förtränger tankar på framtida konsekvenser och
prioriterar att överleva för ögonblicket.
Men idag har vi ingen materiel brist som hotar vår överlevnad. Vi har
allt som behövs för att alla på jorden skall kunna leva.Det är bara
otroligt korkade ledare som tar risken att försöka administrera en
svältande befolkning. Ledare som inte har förstått att hungriga
människor är farliga. Ledare som inte förstått att man blir inte
rikare bara för att någon annan blir fattigare.
När vi vågar lita på att våra fysiologiska behov kommer att tillgodoses
blir frågan: Vad skall vi då ha världen till?
För hundra år sedan var svaret, för en stor del av befolkningen,
givet. Man levde direkt av jorden och uppgiften var att bruka den så
att man lämnade den till nästa generation i minst lika gott skick som
man en gång övertagit den i.
Urbaniseringen och mekaniseringen av jordbruket har emellertid medfört
att vi måste välja nya livsprojekt om vi vill se någon mening i det vi
gör.
Man kan naturligtvis köpa en bil och endast använda den till att stå
i garaget. På samma sätt kan du naturligtvis använda världen till att
enbart tillgodose dina fysiologiska behov. Men det är en tråkig
användning. Även om det är farligt att ge sig ut på vägarna med bilen
ger det intressanta upplevelser och likaså kan det vara motiverat att
ta risken att ta ut världen på projekt som går utöver fysiologisk
överlevnad.
Att lämna din värld i bättre skick än du övertog den är naturligtvis
alltid din uppgift. Och kan du inte själv förbättra den kan du bidra
till att skapa möjligheter för andra att förbättra den.
Att föra brukad jord från generation till generation och att utveckla
och föra hantverkstraditioner och företag vidare är naturligtvis
fortfarande viktiga livsprojekt men det är idag endast en mindre grupp
som har tillfälle att välja dessa. För många av oss gäller att vi inte
får veta att vi måste välja förrän vi kommit så långt i vår utveckling
att vi har mycket svårt att välja sådana mål.
Nedan följer några exempel på mål som man då kan välja.
Bäst i världen
--------------
Din värld innehåller en rad utmaningar som du kan anta om du vill.
Bland annat finns där c:a 10 miljarder människor som du kan mäta
dig mot.
Vid första påseende kan man naturligtvis tycka att bland 10 miljarder
människor måste det väl alltid finnas någon som är bättre än jag. Men
om jag väljer ett tillräckligt smalt intresseområde finns det mer än
10 miljarder intresseområden att välja på. Och jag angriper det område
jag väljer med en unik uppsättning egenskaper och med en unik bakgrund
och uppfostran.
Du kan alltså bli bäst i världen på något och du kan sätta målet allt
högre genom att vidga ditt intresseområde och genom att försöka föra
ut din kunskap till allt större krets. Och att få andra människor att
använda din kunskap för att förbättra sina världar.
Inte sämst
----------
Det finns två slag av ambition:
Överklassambition
Underklassambition
Överklassambition går ut på att vara bra. Att anta allt svårare
utmaningar och lyckas med uppgifter som ingen annan klarar av.
Att höja sig över all jämförelse. Att komma förbi medelklassens
strävan att vara bäst.
Underklassambitionen går ut på att inte vara sämst. Att inte anta
utmaningar och på det sättet komma ifrån risken att misslyckas. Att
ge upp utan att ha försökt.
Krav på rättvisa baseras på underklassambition. Den som vill vara
bättre än bäst kräver inte rättvisa. Det är bara den som inte vill vara
sämst som tar till rättviseargumentet som sista utväg.
Trots att alla människor har egenskaper som gör det möjligt att bli
världsbäst i något avseende tycks det finnas individer med en läggning
som undantränger denna möjlighet till förmån för underklassambition.
Oscar Wilde lär ha sagt: "Egna framgångar är bäst men andras misstag är
inte heller att förakta".
Om du inte förmår att lyckas eller inte vill försöka att lyckas kan du
glädja dig åt att andra misslyckas.
Det här låter dystert men det finns faktiskt en ljuspunkt i det. Det
innehåller en tröst för den som misslyckas. Om jag antagit en alltför
svår utmaning och misslyckats kan jag ändå trösta mig med att jag bjudit
på ett misslyckande som glatt några medmänniskor.
Ibland, om det inte blir för ofta, kan det vara skönt att kunna bjuda på
att vara sämst och därigenom befria någon annan från den uppgiften.
Stödja andra
------------
I din värld ingår även andra människor som du kan använda för att förbättra
den.
I stället för att själv försöka göra allt kan du stödja och uppmuntra andra
som vill ägna sig åt att lösa de problem du ser som angelägna. Ofta är det
tillräckligt att bara avstå från att hindra dem. De flesta människor lever
under ganska likartade livsvillkor. Det som är ett angeläget problem för den
ene är troligen ett angeläget problem även för den andre. Men vi har
skapat samhällen som prioriterar bevarande av det bestående framför
problemlösande förändringar. Att i ett sådant samhälle försöka undvika
att hindra eller kanske till och med hjälpa andra som vill åstadkomma
förbättringar är inte något dåligt livsprojekt.
Fabulöst rik
------------
Intresset för pengar baseras på att pengar fungerar som
uppskattningsbevis.
En gång i tiden var pengar ett skydd mot svält. Den som hade
pengar behövde inte äta barkbröd.Men så är det inte idag. Våra skördar
är större än vad vi orkar äta upp. Vi har en enorm kapacitet för en
datja-ekonomi om vi börjar odla på våra gräsmattor. Det finns alltså
ingen anledning att någon skall behöva svälta. Och skulle det gå så
illa är våra påbudspengar ingenting att lita på. Vi har sett hur
Jugoslaviens pengar blivit värdelösa, vi har sett hur rubeln fått en
helt ny roll med ett helt annat värde än under sovjettiden. Så ingen
som är vid sina sinnens fulla bruk kan samla pengar för att gardera
sig mot svält.
Men ändå samlar människor pengar långt bortom vad de någonsin kan
förväntas behöva. Orsaken är naturligtvis att dessa pengar inte
markerar konsumtionsrätter utan är uttryck för uppskattning.
Att vara till nytta för sina medmänniskor är inget dumt livsprojekt.
Det känns meningsfullt och ger ett ganska behagligt liv. Men ett
problem är naturligtvis hur man kan veta att det man gör verkligen
är till nytta. Ett sätt att få bekräftelse på detta är att ta betalt.
Om dina medmänniskor vill betala för det du gör kan du lita på att
de uppskattar det. Men det förutsätter naturligtvis att de verkligen
vill betala, att de inte luras eller tvingas til det.
Och om du ser pengar som bekräftelse på att dina medmänniskor
uppskattar din insats finns det inga gränser för hur mycket pengar
du kan samla på dig.
Omtyckt av dina närmaste
------------------------
Som alla flockdjur har människan ett behov av bekräftelse och
uppskattning från den flock där hon ingår.
Men tänk på att den uppskattning du kan få genom att följa alla regler
eller genom att jamsa med är kortvarig och i längden kontraproduktiv.
Det är genom att bidra till flockens bästa genom att tillföra sådant
som ingen annan insett som du kan vinna flockens respekt och
uppskattning.
Det räcker inte med att göra allting rätt. Konsten är att göra fel så
att det blir bättre än rätt.
Hatobjekt
---------
"De goda" får lättare att enas och samarbeta om de upplever ett hot
från "de onda". Men det förutsätter att några, eller åtminstone någon,
tar på sig uppgiften att vara "de onda".
Detta är en mycket otacksam uppgift. Troligen kommer nästan ingen att
förstå vilken nytta din insats gjorde och säkerligen kommer ingen att
visa dig någon uppskattning.
Att ta på sig livsuppgiften att vara hatobjekt ställer mycket stora
krav när det gäller självkänsla och förmåga att se sin roll på ett
objektivt sätt.
Förstå hur världen fungerar
---------------------------
När jag i min ungdom fick någon ny sak kunde jag knappt bärga mig
tills den gick sönder så att jag fick plocka isär den och se hur den
var gjord. Entusiasmen inför varje detalj har väl svalnat med åren men
världen innehåller tillräckligt mycket som ännu är okänt för att alla
skall kunna finna livsuppgifter med att plocka isär och se hur den är
gjord. Och skulle vi någon gång komma att förstå alla konstruktions-
principer finns obegränsade uppgifter som går ut på att använda denna
kunskap.
Som exempel på frågor som vi inte vet svaret på kan nämnas:
Varför kondenserar materia till elementarpartiklar?
Varför är förhållandet mellan protonmassa och elektronmassa
c:a 1800?
Varför upprepas mönsterdetaljer?
Varför finns det ett samband mellan orsak och verkan?
Hur avgör vi vad som är ont och gott?
I strävan att förstå materiens innersta väsen bygger vi allt
större och dyrare instrument. Vi beter oss som utomjordingar som
fått tag på en sedel och försöker förstå vad den är till för
genom att granska den med allt större mikroskop. Men det finns
ingen anledning att tro att det blir den som har största
mikroskopet som kommer på att sedeln används som betalningsmedel.
Vem som helst har lika stor möjlghet att inse det. Och det samma
gäller för världen. De fakta som partikelfysikerna gräver fram
kan vara intressanta att ta del av men du har lika goda möjligheter
som någon annan att sätta in dessa i ett begripligt sammanhang.
Översätta världens språk till och från mänskligt
------------------------------------------------
För några hundra år sedan påbörjades arbetet att med hjälp av matematik
skapa ett mellanspråk mellan världens och människors språk. Naturlagar
fick formuleringar i form av formler som kunde användas för beräkningar.
Datatekniken öppnar nu ytterligare en möjlighet att skapa ett mellan-
språk.
I formler måste man arbeta med storheter som kan anta ett (skalar) eller
ett begränsat antal (vektor) siffervärden. Och manuella beräkningar blir
så långsamma och mödosamma att man måste nöja sig med att räkna igenom
ett fåtal intuitivt valda exempel.
Med datateknik öppnas möjligheter att inte bara använda formler utan
även att skriva program som använder andra program.
Datatekniken har även öppnat möjligheter till snabba beräkningar. Vi
är på väg att kunna använda varje nanosekund och det finns nästan lika
många nanosekunder på en sekund som det finns sekunder på ett människoliv.
Ytterligare en möjlighet som nyligen tillkommit är att hämta färsk
information och att lämna ut information till allmänt beskådande. Även om
vi ännu inte lärt oss att hantera dessa möjligheter kommer de att medföra
möjligheter att diskutera med likasinnade även i frågor som är så speciella
att de endast intresserar ett fåtal människor i hela världen. Denna
möjlighet gör att du kan komma åt praktiskt taget all befintlig och
verbaliserad kunskap.
Vi har alltså på några få år fått helt nya möjligheter att skapa
mellanled mellan vårt talade mänskliga språk och det språk som världen
förstår.
Samtidigt med att dessa möjligheter öppnas börjar vi ana hur de
program som ligger i våra gener är uppbyggda.
På några få år har vi fått dramatiskt ändrade förutsättningar att
kommunicera med vår omvärld men användningen av dessa möjligheter är
ännu tafatt och förvirrad. Vi behöver utveckla de språkliga mellanleden
och deras anknytning dels till mänskligt språk dels till det språk som
världen förstår.
Här finns, praktiskt taget, obegränsade möjligheter att ta fram nya
element i denna översättning, från detaljer som utformning av en
tryckknapp till skapande av ett operativsystem eller dekompilering av
programmet för ett hormonsystem.
Långsiktig uppgift
------------------
Ett sätt att se mening med livet är att ägna sig åt människans
långsiktiga uppgift, åt det som kommer att spela någon roll
miljontals år framåt i tiden.
Det mesta av det som vi nu betraktar som viktigt kommer att helt
förlora betydelse redan om några tusen år. Men det finns en sak som
människan, och endast människan, gör. En sak som är nödvändig för att
livet på jorden skall kunna bestå på lång sikt. En sak som rättar till
en obalans i livscykeln, en obalans som funnits i miljontals år och som
minskat utrymmet för liv på jorden.
Allt liv är baserat på kol. Kolföreningar ingår i alla organismer och
kolet vandrar runt från organism till organism. Men det finns ett litet
svinn.
Under årmiljoner har kolföreningar som inte tagits upp av nya organismer
bildat stenkol, olja, naturgas, brunkol och torv och därmed dragits bort
från livscykeln. Livet har anpassat sig, bl a genom att dagens växter kan
utnyttja en atmosfär med mycket låg halt koldioxid. Men tillgången på
koldioxid är begränsande för växternas tillväxt och möjlighet att
tillvarata solljus. I en atmosfär med förhöjd koldioxidhalt kan man få
växter att växa betydligt snabbare och alltså tillvarata solljuset bättre
och omvandla det till energirika näringsämnen.
För att inte ännu mer kol skall undandras måste någon börja återföra de
koldepåer som byggs upp. Människan är den första och enda varelse som gör
detta.
De tidiga livsformerna åstadkom en enorm "miljöförstöring" när de omvandlade
jordens koldioxidatmosfär till en syreatmosfär. Människans uppgift är att
avsluta denna omvandling och balansera kolflödet. Men det gäller att
balansera kolflödet, inte att återföra kol så snabbt att vi inte hinner
anpassa oss.
Alla människor har alltså en långsiktig uppgift. Även om din del av denna
uppgift är liten är den betydelsefull.
Reglage och styrmedel
=====================
Orsak och verkan
----------------
Världen förändras hela tiden. Det är dessa förändringar som är tiden.
Varje gång en urskiljbar punkt utsätts för en detekterbar lägesförändring
någonstans i världen inträffar en enhetshändelse och varje gång en
enhetshändelse inträffar går tiden en tidsenhet. Om ingenting i hela världen
förändras går inte tiden.
Världen har egenskapen att händelser kan samordnas så att om händelse A
inträffar ökar sannolikheten för att händelse B skall inträffa. Om
framändan av en bil förflyttas ökar sannolikheten att även bakändan
skall förflyttas. Varför det är så vet vi inte och vi har knappast ens
ställt oss den frågan. Vi har upplevt detta som en egenskap hos
världen som är så fundamental att vi tar den för självklar.
Om händelse A ökar sannolikheten för händelse B säger vi att A orsakar
B. Vi kallar A för orsak till B och vi kallar B för verkan av A.
När du jämför världen med dina önskemål kan du finna att den avviker
från önskemålen. Skillnaden bildar en felsignal som du kan använda för
att åstadkomma en orsak som medför att felsignalen minskar, d v s att
den verkliga världen närmar sig dina önskemål. Och kan du inte direkt
åstadkomma en orsak som ger önskad verkan kanske du kan åstadkomma en
orsak som ger en verkan som orsakar den önskade verkan, eller en orsak
till en orsak till en orsak till önskad verkan.
Ett mellanled som vi använder för att åstadkomma en verkan som kan
användas som orsak till den verkan vi vill åstadkomma kallas för servo.
I princip kan vi skilja mellan tre typer av servon
Högre makter
Andra människor (och andra levande varelser)
Fysikaliska fenomen.
Dessa servon används på olika sätt och de läror som beskriver hur de
kan utnyttjas kallas
Religion
Psykologi,Språk,Ekonomi
Fysik
Servon
------
Religion
.........
Religion handlar om verkan som vi inte vet någon pålitlig orsak till.
Gödel har visat att vi inte inom ett system kan ställa upp ett system
av teorem som är fullständigt och motsägelsefritt. Vi måste anknyta
systemet till något som ligger utanför det. Detta gäller även för världen.
Heisenberg har visat att vi inte kan göra exakta mätningar vilket innebär
att vi inte heller exakt kan få reda på sambandet mellan orsak och verkan.
Ju mer vi har lärt oss om samband mellan orsak och verkan ju mer har vi
flyttat bort från religionens område men vi kan alltså visa att det alltid
kommer att finnas en osäkerhet som vi inte kan hantera med hjälp av
naturlagar eller av varandra. Vi föreställer oss då att det finns något
väsen som står utanför världen. Ett väsen som inte är underkastat de
begränsningar som Gödel och Heisenberg påpekat. Religion är läran om
hur vi kan kommunicera med detta väsen.
Religion handlar alltså om att påverka det vi inte kan förutse.Oförut-
sedda händelser inträffar men det finns inget sätt att avgöra om de
verkligen påverkas av våra försök att påverka dem. Varje oförutsedd
händelse är unik och vi kan aldrig veta vad som skulle ha hänt om vi
inte försökt påverka den.
För c:a 10 000 år sedan föddes underkastelsereligioner. Man konstaterade
att det var omöjligt att säkerställa önskad verkan och övergick till att
i stället anpassa önskan till verkan. Man predikade foglighet d v s
underkastelse under en påbjuden vilja. Detta möjliggjorde samordning som
i sin tur möjliggjorde skapande av högkulturer där människor kuvades
under en vilja som utformades av en styrande elit. Men ett sådant
samhälle bryter lätt samman när den styrande eliten inte längre förmår
generera engagerande mål. Det gångna årtusendets utveckling har,i stor
utsträckning,baserats på att allt mer flyttats bort från religionens
område och därmed bort från underkastelsedogmen.
Religion använder följande begrepp:
Verkan: Underverk
Orsaksmängd: Bön , rit
Orsaksintensitet: Helighet
Ekonomi
.......
Det finns flera olika sätt att använda andra människor som orsak till
den verkan du vill åstadkomma. Det system som är bäst formaliserat och
lättast att beskriva är ekonomi. Ekonomi kan ses som en formalisering
av psykologi, språk mm där syftet att använda andra människor som orsak
till önskad verkan lyfts fram.
Ekonomi använder följande begrepp:
Verkan: Nyttighet
Orsaksmängd: Penningbelopp
Orsaksintensitet: Penningvärde
(Mer om ekonomi kommer i en planerad handbok för samhällsägare)
Fysik
.....
Fysik använder naturlagar för att beskriva samband mellan orsak och
verkan. Det handlar om att beskriva situationer på sådant sätt att man
kan ange vad som troligen kommer att hända. Det handlar alltså om att
beskriva förutsägbara förändringar och de förutsättningar som skall
vara uppfyllda för att dessa skall inträffa.
Förutsägbara förändringar kallas för energi.
När det gäller att beskriva orsaker delar man in fysik i flera olika
delområden som använder olika begrepp. Exempel på sådana delar är ellära,
värmelära och mekanik.
Fysik använder följande begrepp:
Ellära Värmelära Mekanik
Verkan: Energi Energi Energi
Orsaksmängd: Laddning Entropi Kraft
Orsaksintensitet: Spänning Temperaturskillnad Väg
Adresserbara ventiler
=====================
I en jämnt fördelad världseter kan inga punkter urskiljas. Där finns
inga punkter som kan ändra läge i förhållande till varandra. Det
innebär att inga händelser kan inträffa.Varken begreppet rum eller
begreppet tid har någon mening i en sådan värld.
Men din värld ser inte ut på det viset. Den vimlar av urskiljbara
avvikelser. En del av dessa är så osannolikt stora att du kan förutse
att de kommer att utjämnas. De är alltså energi, d v s förutsägbara
förändringar, d v s användbar verkan. Sådan förutsägbar verkan kan du
använda som orsak till annan verkan som du önskar åstadkomma.
I många fall utjämnas inte osannolikt stora avvikelser på grund av
att utjämningen hindras av någon barriär. Om du kan öppna en sådan
barriär med en ventil som du kan styra har du fått ett sätt att
styra ett orsaksflöde.
En adresserbar ventil är den vanligaste servokomponenten.
Exempel 1
Eldningsolja är ett osannolikt tillstånd. Du kan förutse att den
kommer att övergå till koldioxid,vatten och värme.Men övergången
hindras av två barriärer, en temperaturbarriär och en ytbarriär. Vid
rumstemperatur sker övergången så långsamt att värmeavgivningen är
försumbar. Och för olja i en dunk eller dylikt är den yta där oljan
är i kontakt med luften så att övergången kan ske så liten att
övergångshastigheten blir försumbar.
Om du vill använda olja som orsak till värme som håller ditt hus
varmt behöver du bryta barriärerna med någon typ av ventil som du
kan adressera och styra så att du får lagom varmt i huset.
Du använder en oljebrännare som adresserbar ventil. I den finfördelar
du oljan till små droppar med stor yta och i den håller du så hög
temperatur att oljan brinner.
I oljan har du en orsaksmängd i form av en oljemängd. Du har en
orsaksintensitet i form av oljans brännvärde. Oljan kan orsaka verkan,
d v s energi i form av värme. Du utlöser orsaken med en adresserbar
ventil i form av en oljebrännare. När du adresserar denna genom att
starta den får du ett orsaksflöde genom den som ger ett verkansflöde
i form av ett värmeflöde som håller varmt i ditt hus.
Exempel 2
På ditt bankkonto kan du ha en penningsumma. Denna kan du använda som
orsak till att andra människor utför arbete åt dig. Penningbeloppet är
orsaksmängd och penningvärdet orsaksintensitet. Men denna orsaksmängd
omges av en barriär som består i att banken inte lämnar ut pengarna.
Om du vill använda pengarna som orsak, t ex till att få ett hus byggt,
behöver du bryta barriären med någon typ av ventil som du kan
adressera och styra till de arbeten du vill ha gjorda.
Du använder beställningar och fakturabetalningar som adresserbar
ventil.
Från bankkontot flyter ett orsaksflöde i form av ett penningflöde med
en orsaksintensitet i form av ett penningvärde. Detta orsaksflöde ger
ett verkansflöde i form av ett arbetsflöde som skapar ditt hus.
Inte bara förändring
====================
När du ser dig om i din värld finner du att den vimlar av potentiella
orsaker. Orsaker som du kan utlösa som förändringar.
Men förändring är inte alltid det samma som förbättring. Det gäller att
välja förändringar som fungerar som steg mot förverkligande av ditt
livsprojekt. Och det gäller att nå önskad verkan med minsta möjliga
oönskade biverkan.
De förändringar du kan utlösa fungerar som bokstäver i en bok. De kan
liksom bokstäverna sammanställas och bilda ett budskap.Och det är
detta budskap som är viktigt. Att åstadkomma en stor mängd bokstäver
har inget värde. Tvärtom är det bättre ju färre bokstäver du behöver
använda för att få fram budskapet.
Och den innersta kvintessensen av ditt budskap måste du och ingen annan
komma på hur du får fram.
Att vi vill lyssna på en skicklig musiker beror inte på att vi då får
höra alla toner med exakt de tonhöjder, de ljudvolymer och de varaktig-
heter som anges i notbladet. En maskin som åstadkommer detta med mycket
hög precision ger en föga njutbar musik. Musikerns skicklighet ligger
i att göra fel så att det blir bättre än rätt. Att lägga in små, nästan
omärkliga, avvikelser som får oss att vilja höra mer.
Ytterst bygger ditt livsprojekt på din förmåga att utveckla en sund
galenskap. En förmåga att "få till det". Att inte bara åstadkomma
förändringar enligt de regler som du fått lära dig utan också göra
avvikelser som är uttryck för din vilja. Att ta risken att visa din
vilja.
Att visa din vilja för din värld är som att dra i startsnöret på din
utombordsmotor och visa motorn din vilja att den skall starta. I bästa
fall möter du uppskattning och motorn startar. I värsta fall får du
mothugg och rycker av startsnöret.
Innan du första gången drar i startsnöret på din utombordsmotor kan det
vara lämpligt att du frågar dem som har använt liknande motorer hur du
bör ställa in gas och choke. Och det kan vara lämpligt att ta emot råd
innan du försöker visa din vilja för resten av din värld. Men hur du sen
väljer att ställa in utombordsmotorn eller resten av din värld är din
sak.
Garantivillkor och varningstext
===============================
Världen är en komplicerad produkt med många användningsmöjligheter. Bl a
innehåller den utmaningar som blir intressanta att anta därför att
resultatet inte är givet. Att lyckas är inte särskilt roligt om man inte kan
misslyckas. Världen måste därför innehålla även risker och svårigheter. Detta
är inte något fel och därmed inte något som kan reklameras.
Din värld kan vara lätthanterlig eller svårhanterlig jämfört med andras
världar. Men även de värsta måndagsexemplaren innehåller enorma möjligheter
som du kan utnyttja. Och det är din uppgift att förbättra din värld.
Genom att börja använda programmet "Liv" bekräftar du mottagandet av din
värld, accepterar dess egenskaper, får tillgång till dess möjligheter och kan
börja förändra den enligt dina önskemål. Att programmet "Liv" fungerar innebär
att din värld fungerar i en utsträckning som gör reklamationer obefogade.
Många religioner har visserligen vad som skulle kunna kallas "reklamations-
formulär", t ex ritual för förbön, med krav på att vissa världsegenskaper
skall kompenseras i denna eller kommande tillvaro men ingen har kunnat visa
att dessa har någon verkan.
Världen levereras alltså i befintligt skick utan någon garanti. Du kan
inte reklamera egenskaper hos din värld men du kan förändra den så att
den bättre överensstämmer med dina önskemål.
Världen gör vad du ber den om. Det finns inga spärrar mot katastrofal
verkan. Hur förödande resultat du än ber om verkställer världen din
begäran om du bett på ett sätt som den förstår. Vill du gardera dig mot
katastrofala misstag måste du själv förändra världen och förse den med
säkerhetssystem.
Vill du ha skyddsräcken måste du själv sätta upp dem. De ingår inte i
leveransen!!!
DEL 2
Vad är teknik?
==============
Vi ser på vår omvärld och vi jämför den omvärld vi ser med den vi önskar
oss. Skillnaden bildar en felsignal. Teknik är konsten att förändra
omvärlden så att denna felsignal minskar.
Teknik handlar alltså om förändring och för att kunna hantera förändringar
behöver vi något kvantitativt mått på förändring. Kvantifierbar förändring
kallar vi energi.
För att närmare beskriva energi brukar vi använda en uppdelning där energi
betraktas som en produkt av två faktorer. En faktor anger den mängd som
förändras (extensiv faktor) och en anger hur mycket varje mängdenhet
förändras (intensiv faktor).
Energiform Extensiv faktor Intensiv faktor
El Laddning Spänning
Lägesenergi Tyngd Höjd
Rörelseenergi Impuls Hastighet
Arbete (tekniskt) Kraft Väg
Värme Entropi Temperatur
Eftersom "entropi" är värmelärans motsvarighet till ellärans "laddning"
eller mekanikens "tyngd" kallas entropi ibland för "värmeladdning" eller
"värmetyngd".
Storleken på den extensiva faktorn beror på hur vi avgränsar vårt system.
Om vi har varmt vatten i en hink har vi värmeenergi i vattnet. Häller vi ut
en del av vattnet minskar värmeenergin i hinken. Entropin i hinken minskar
men temperaturen förblir oförändrad. Värme förblir värme även om det värme
som finns i hinken minskar.
Förändring av den intensiva faktorn kan innebära att energi övergår från en
form till en annan. När en kula faller från ett bord minskar dess höjd.
Lägesenergi omvandlas till rörelseenergi. Och låter vi värmet i hinken driva
en Stirlingmotor av lågtemperaturtyp sjunker temperaturen när värme övergår
i arbete.
När det gäller extensiva faktorn finns i allmänhet en självklar nollpunkt att
utgå från. Vi kan välja en nollpunkt som är sådan att enbart positiva värden
kan förekomma. Som vi ser världen förekommer inte begreppet "negativ mängd".
När det gäller intensiv faktor däremot har det för t ex temperatur inte varit
självklart hur man skall välja nollpunkt. Men man kan mäta temperatur med
volymen hos en gas som hålls vid konstant tryck och om man då sätter
nollpunkten vid den temperatur som ger volymen noll får man en självklar
nollpunkt som gör att temperatur alltid blir en positiv storhet.
Om man väljer nollpunkter för intensiv faktor på lämpligt sätt finner man
att alla energiomvandlingar sker så att totala energimängden förblir konstant
det är bara fördelningen mellan olika energiformer som ändras.
(Termodynamikens första huvudsats).
Termodynamikens första huvudsats är ett mycket viktigt hjälpmedel när
det gäller att förutsäga vad som kommer att hända vid en energiomvandling.
För att vi skall kunna förändra vår omvärld så att felsignalen mellan den
omvärld vi ser och den vi önskar minskar måste vi ha tillgång till
förutsebara förändringar. Om vi vill ha varmt i rummet där vi sitter
behöver vi någon sorts uppfattning om hur mycket ved vi bör lägga in i
kaminen. Tack vare första huvudsatsen kan vi, mycket exakt, beräkna hur
mycket ved som går åt.
Men första huvudsatsen räcker inte. Den säger inte att veden kommer att
brinna och ge värme till rummet. Det strider inte mot första huvudsatsen
att processen går åt motsatt håll d v s att aska, koldioxid och vattenånga
tar värme från rummet och återbildar ved.
I de flesta fall har vi klart för oss åt vilket håll en process kommer att
gå. När vi eldar i en värmepanna tar vi för givet att värme skall gå från
den varma lågan till det svalare vattnet. Men för att mer i detalj kunna
förutsäga vilka förändringar som kommer att uppträda vid energiomvandlingar
behöver vi en mer stringent formulerad naturlag.
När man började göra maskiner som omvandlade värme till arbete (ångmaskiner,
varmluftmaskiner mm) fann man att värme vid hög temperatur spontant spred sig
så att temperaturen sjönk. Värmeenergi är ju entropi gånger temperatur så om
temperaturen för en konstant energimängd minskade måste dess entropi öka.
Däremot lyckades man aldrig få entropin för ett slutet system att minska så
att temperaturen ökade. Man konstaterade att "Entropin hos ett slutet system
kan inte minska". (Termodynamikens andra huvudsats)
Även om inte entropin hos ett slutet system kan minska kan entropin minska hos
ett öppet system d v s hos ett system som utbyter energi med omgivningen. När
vatten fryser till is avges värme vid konstant temperatur. Om temperaturen är
konstant kan vattnet bara avge energi genom att dess entropi minskar. Den
energi som avges är entropiminskningen gånger absoluta temperaturen. Man kan
se det som att den entropi som försvinner går ner till absoluta nollpunkten i
temperatur för att där försvinna.
Entropin vid absoluta nollpunkten är alltså noll. (Termodynamikens tredje
huvudsats)
Vår villiga värld
=================
"Bed och ni skall få".
Vår omvärld uppfyller alla våra önskemål. Det är bara ett krav som vi måste
uppfylla: Vi måste uttrycka oss så att omvärlden "förstår" vad vi vill.
Om jag vill att en sten skall flytta sig kan jag försöka säga: "Flytta dig"
på olika språk. Men jag upptäcker snart att det inte hjälper. Stenen "förstår"
inte språket. Inte ens om jag ilsknar till och börjar svära händer det något.
Men när jag blir ännu ilsknare och börjar sparka på stenen närmar jag mig ett
språk som den förstår. Är den liten kan det rent av resultera i att den
flyttar sig.
Fysik är läran om det språk som död materia förstår. Som andra språk består
detta språk av språkelement som binds samman av regler som kan kallas
språkets grammatik. Men i fysik är inte språkelementen ljudkombinationer som
i talade språk. Exempel på fysikens språkelement är partiklar, krafter,
längder d v s mängder och intensiteter. Och exempel på grammatiska regler
som binder samman språkelementen är termodynamikens huvudsatser.
När jag vill tala om för stenen att jag vill att den skall flytta sig är det
därför ingen ide att använda talat språk. Jag måste i stället använda krafter
som informerar stenen om mina önskemål. Och jag måste med dessa krafters
storlek tala om hur stark min vilja är och med deras riktning vartåt jag vill
att den skall flytta sig. Gör jag det på rätt sätt "förstår" stenen vad jag
vill och gör exakt vad jag bett den om.
Alla levande varelser behärskar det fysiska språket i någon grad även om
uttrycksförmågan hos ett grässtrå är ganska begränsad. Vid sidan av det
fysiska språket har insekter utvecklat kemiska språk och människor har
utvecklat ljud- och bildspråk. Men även människor föds med enbart ett
fysiskt språk. När vi växer upp ökar våra uttrycksmöjligheter så att vi
börjar bli farliga för vår omgivning. I takt med det lär vi oss att tala
och tänka i ord så att vi kan kan testa handlingar i en symbolvärld innan
vi vidtar dem och därigenom avstå från sådant som kan skada oss själva och
vår omgivning. Men många har till en början problem att uttrycka sig med
tal och vill gärna ta till ett handgripligt fysiskt språk för att göra sig
förstådda. Vi har därför ett starkt socialt tryck för att undertrycka det
fysiska språket. Så starkt tryck att vi slutar uppfatta det fysiska språket
som det språk det är. När vi sedan går tillbaka och läser fysik för att
lära oss använda det fysiska språket uppfattar vi ofta inte vad vi gör.
Vi lär oss fysik som hokus pokus.
För att få vår vilja igenom behöver vi kunna ta i. Vi behöver ge eftertryck
åt det vi säger. I talade språk gör vi det genom att höja rösten och övergå
till att skrika. I fysikens språk gör vi det genom att ta i med större kraft.
Men vi lär oss så småningom att detta inte är någon bra metod. Vad vi säger
är viktigare än hur vi säger det. Vi har större möjlighet att få vår vilja
fram om vi framställer den så att den sammanfaller med andras intresse.
Och med fysikens språk behöver vi ta i mindre om vi utnyttjar förutsägbara
förändringar. Om jag bara vill rulla bort en sten i en slänt behöver jag
ta i betydligt mindre om jag rullar den utför än om jag rullar den uppför.
Och är den stor är det bättre att meddela den min vilja via ett spett än
att ta tag i den direkt.
Människor har i alla tider vetat hur man använder ett spett. Men för att
kunna uttrycka sig så bra som möjligt med det skulle vi behöva översätta
spettets fysiska språk till vårt talade språk så att vi kunde använda hela
den överbyggnad av abstrakt tänkande som vi skapat kring vårt talade språk.
För ett par hundra år sedan upptäckte man att matematik kan användas för
sådana översättningar. Man fann att om man vill ha stor kraft (Fu) från
ett spett får man liten förflyttningssträcka (Lu) och detta åstadkommer
man med en liten kraft (Fi) och en stor förflyttningssträcka (Li). Man
kunde formulera spettets grammatiska regel som
Fu x Lu = Fi x Li
Och därmed kunde vi börja diskutera spettanvändning med betydligt större
precision än tidigare. Man kunde börja stuva om formeln. För att få veta
hur stor kraft man behövde ta i med (Fi) för att få kraften Fu kunde man
skriva den
Fi = Fu x Lu/Li
När man insåg att Lu/Li var lika med förhållandet mellan hävarmarna kunde
man mycket exakt förutsäga hur spettet förmedlade vårt önskemål till
stenen.
När vi använder ett spett har vi intuitivt klart för oss hur vi bör välja
angreppspunkt och stödpunkt. Lyckas vi inte rubba stenen söker vi en ny
stödpunkt som ligger närmare angreppspunkten.
Detta fungerar bra i den direkta arbetssituationen men om vi vill planera
ett arbete på ett ingenjörskontor behöver vi det matematiska språket för
att kunna veta vilka resurser som behöver sättas in för att åstadkomma
önskat resultat. Vi behöver t ex kunna svara på frågan "Hur långt spett
skall vi skicka med gubben som skall flytta stenen?". Vi vill inte skicka
med ett alltför långt så att han får bära ett onödigt tungt spett och inte
ett så kort att han blir tvungen att gå hem och byta. För att svara på denna
typ av frågor kan vi ha stor hjälp av matematiska formuleringar av det
fysiska språkets grammatik.
Ju mer vi lär oss hur vi kan uttrycka våra önskemål ju mer inser vi att
våra tillkortakommanden inte beror på en vrång omvärld utan på att vi
uttryckt våra önskemål på klumpiga sätt.
Jag hörde en gång på radio en intervju med en kvinna som sade sig kunna
tala med hästar. Hon berättade att hon blivit anlitad av en hästägare som
hade en ovanligt svårhanterlig häst. Hon satte sig i spiltan, lyssnade på
den och upptäckte att den sa: "Jag försöker, men jag förstår inte vad de
säger". Hon gav ägaren rådet att uttrycka sig tydligare och efter det
blev hästen lydig.
Om någon kunde tala med vår omvärld skulle även den säga: "Jag försöker,
men jag förstår inte vad de säger". Men ju tydligare vi uttrycker oss
ju lydigare blir omvärlden.
Om att slå och kasta
====================
Vad man vinner i kraft förlorar man i väg.
Denna regel i fysikens grammatik är lika viktig som an,auf,hinter,in...
är i tysk grammatik.
Vi kan utnyttja denna regel med hjälp av en hävstång. Men vi har också en
medfödd instinkt att använda den på ett annat sätt. Bland de första rörelser
vi gör som nyfödda är slagrörelser. Vi sätter med ringa kraft fart på något,
t ex på en hand, under en lång accelerationssträcka för att få en stor kraft
vid inbromsningen.
När barn känner att deras förmåga att argumentera med ord inte räcker
till vänder de sig till det kraftigaste fysiska uttrycksmedel de har
tillgång till d v s till slag och sparkar.
När jag skall klyva ved är det självklart att jag tar till en yxa. Yxan
dras nedåt av sin egen tyngd och dessutom pressar jag den nedåt med skaftet.
Kraften på yxan rör sig om
Fi = 100 N
Yxans fallhöjd ned till vedträt kan röra sig om
Li = 1 m = 1000 mm
Antag att huggkubbe och vedträ sviktar 1 mm vilket ger
Lu = 1 mm
så får jag alltså kraften Fu i islagspunkten enligt
Fi x Li = Fu x Lu
vilket ger
Fu = 100000 N
Ett vanligt yxhugg skulle alltså, om inte materialet sviktade, kunna lyfta
en 10 tons lastbil 1 mm. Eller också kan man se det som att ett sådant
yxhugg ger samma kraft på yxeggen som om man kört upp en 10 tons lastbil
på yxan.
Men hur mycket materialet sviktar har avgörande betydelse för resultatet.
Tar jag ett kort vedträ av hårt träslag och ställer det direkt på en
berghäll kanske jag kan minska svikten till 0,1 mm och få samma kraft i
islagspunkten som om yxan vägde 100 ton (fast risken att jag förstör yxan
genom att den går rakt i berget med ännu mindre svikt och därmed ännu
större kraft är överhängande).
Ställer jag däremot vedträt på den mjuka gräsmattan får jag större svikt
och därmed mindre kraft även om vedträts egen massa ger ett visst mothåll.
En variant av slaget är kastet. I princip kan jag avsluta ett yxhugg med att
släppa yxan innan den når fram till vedträt. Yxan fortsätter ändå fram till
vedträt och slår i med stor kraft. Och om jag riktar hugget mot en vägg några
meter bort och släpper yxan far den iväg mot väggen och slår i.
Förmågan att hantera kast är antagligen en väsentlig orsak till att människan
blev framgångsrik som art. Även andra arter, t ex apor, kastar föremål men
det är bara människan som lyckats utveckla kasttekniken med hjälp av
kasthjälpmedel. Och att med kast kunna döda ett byte eller en fiende på
avstånd spelade naturligtvis en stor roll när det gällde att överleva på
stenåldern.
När jag kastar en sten rör den sig framåt samtidigt som den faller nedåt.
Om jag kastar den rakt fram blir den tid det tar för den att falla till
marken oberoende av stenens vikt och av hastigheten framåt (om jag riktar
kastet snett uppåt tar det längre tid innan den når marken men då går den
också långsammare framåt). För att komma så långt som möjligt gäller det
då att få högsta möjliga utgångshastighet på stenen så att den hinner så
långt som möjligt innan den når marken. Det talar för att jag bör välja en
lätt sten som jag orkar sätta fart på.
Men min hand och arm väger en del och musklerna arbetar inte oändligt snabbt.
Även om jag gör en kaströrelse utan någon sten finns det därför en gräns för
hur stor hastighet jag kan uppnå. Och om jag minskar stenens vikt går allt
större del av muskelarbetet åt till att sätta fart på hand och arm och allt
mindre till att sätta fart på stenen. När man skall kasta sten på byte eller
fiende bör man alltså välja en stenstorlek som är anpassad till musklerna och
till massan hos hand och arm.
Om man kunde slippa sätta fart på hand och arm skulle man kunna få ett
effektivare kast.
Med en slunga kan man åstadkomma att kaststenen får högre hastighet än
handen. En teknik som bara människan kommit på. Och utvecklingen av pilbågen
gjorde det möjligt att skicka iväg en pil utan att mer än en del av den
tunna bågsträngen behövde komma upp i pilens utgångshastighet. Och i ett
gevär lyckas vi driva upp kulan i överljudsfart utan att mer än en del av
krutgaserna behöver komma upp i denna hastighet.
Som vid ett slag gäller för ett kast att Fi x Li bestämmer hur stor kraft
Fu som vi får ut vid islagspunkten om materialet där sviktar med sträckan
Lu. Och Fi x Li bestämmer också, tillsammans med projektilens massa hur
stor utgångshastigheten blir och därmed hur långt kastet blir.
Poängen med ett gevär är att man kan driva upp en liten kula i mycket hög
hastighet. Om man kastar en gevärskula når man mycket snabbt upp till den
högsta hastighet som man kan röra handen med. Den sträcka där man sätter
fart på kulan (Li) blir alltså kort. Därefter följs bara hand och kula åt
utan att handen påverkar kulan med någon kraft. Vi får alltså ett lågt
värde på Fi x Li och kastade gevärskulor är knappast något att bry sig om.
Vid ett kast blir Fi x Li projektilens rörelseenergi. När man skjuter med
ett gevär får man kraften Fi på såväl kulan som geväret. Om Fi är stor slår
den omkull skytten. Och Li är högst pipans längd. Det går alltså inte att
få särskilt hög rörelseenergi hos kulan. Den blir betydligt större än om
man kastar en gevärskula men inte nämnvärt större än rörelseenergin hos en
yxa som man kastar. Men som vi såg ovan kan ett yxhugg ge rejäl kraft vid
islaget och poängen med ett gevär är att man kan få denna rörelseenergi
hos en liten kula, en kula som är så liten att den får mycket hög hastighet
och därmed blir kastet långt.
Genom att förfina kasttekniken har vi alltså lärt oss hur man kan sitta
bekvämt i ett jakttorn och tala om för en älg att det är dags att falla.
Slungan, pilbågen, kastmaskinen, armborstet, kanonen, geväret, revolvern
ställde allt större krav på formulering av de regler som bestämde en
projektilbana. Försöken att stöpa silverkula i tron att skytten då fick
bestämma banan första och andra gången men att djävulen bestämde den tredje
banan visade sig inte fungera. Man fick betydligt mer tillförlitliga
resultat med matematiska beskrivningar av projektilbanor.
Teknikens grundstenar
=====================
Teknikens första grundsten var strävan att underlätta framtagande av livets
nödtorft. Att kasta sten eller metallbitar på bytesdjur, att slå på jorden med
en hacka för att få bort ogräs, att åstadkomma klimatskydd med väggar och tak
var teknik som visade omvärlden hur den skulle förse människorna med det de
behövde.
Men till detta kom också så småningom en annan viktig grundsten.
När människan övergick till jordbruk behövde man en sammanhållning i fastare
samhällen. För att det skulle vara meningsfullt att så på en åker måste man
kunna lita på att man även skulle kunna få skörda på den. Man behövde en
överhet som kunde ta itu med dem som försökte skörda vad de inte sått.
Men vem skulle vara överhet? Och hur skulle överheten visa att den var värd att
lyssna på?
En utmärkt beskrivning av hur man legitimerar och upprättar en sammanhållande
överhet finns i Moseböckerna i Gamla Testamentet. Där berättas om hur Mose
skapar en överhet som kan hålla samman halvvilda nomadstammar under 40 års
ökenvandring.
En viktig orsak till att Mose lyckades med denna svåra uppgift var att han
hade en kunskap om hur man kan använda oljefraktioner. Han kunde frammana
ljud,ljus,rök och tryckvågor. Och han använde detta som bevis på att han
stod i förbund med en allsmäktig gud. Ett förbund där all kommunikation
mellan gud och folket måste gå genom honom. Och där alltså han hade en
obestridlig ledaruppgift.
Även på andra håll växte det upp samhällen som på liknande sätt hölls samman
av en liten elit som skaffade sig speciella kunskaper som de hemlighöll för
resten av folket. Teknik blev ett medel att imponera på folket och legitimera
överhetens åtgärder.
En viktig sådan kunskap var almanackan. Brahmanen som kunde förutsäga när det
var dags att brygga soma och åkalla Indra kunde man nog anförtro uppgiften
att hålla efter slöddret i samhället. Men naturligtvis avslöjade inte
Brahmanen vilka enkla knep han använde för att följa solståndet.
En annan teknik som använts för att imponera är konsten att bygga stora
byggnader. När man lärde sig att bära upp tak med valvbågar kunde man börja
bygga enorma kyrkor. Inte för att man hade något behov av sådana byggnader
utan därför att människor blev imponerade av att de kunde stå utan att rasa.
Och hur det gick till blev en hemlighet som förvaltades inom en mycket
liten krets.
Och det var inte bara Mose som knöt hantering av eld till en gud. Brännoffer
förekom i många religioner och en så farlig hantering som eldning omgärdades
med omfattande ritualisering. Men här fanns ett påtagligt dilemma.
Eld är både imponerande och användbar. Hur skulle man kunna använda eld
samtidigt som överheten hemlighöll eldningstekniken för att imponera med den?
Mose löser problemet genom att låta folket hantera vedeldning men han
hemlighåller hur man hanterar oljefraktioner.
På detta sätt har teknisk kunskap tagits fram och hållits inom en liten elit,
så liten att betydande delar gått förlorad och måst återupptäckas när vissa
personer tagit med sig delar av den i graven.
Att kunskap om olja idag sprids på ett helt annat sätt än på Moses tid beror
inte på någon större öppenhet från överhetens sida. Orsaken är att överheten
idag förfogar över atombomber som imponerar så att man inte behöver oljan för
det.
Men när man läser teknik är det viktigt att komma ihåg att en av grundstenarna
är en hemlig tradition. Liksom kyrkan en gång i tiden försökte utestänga
pöbeln genom att tala latin har man inom tekniken använt ett matematiskt språk.
Detta är motiverat av att det faktiskt fungerar som översättare mellan fysik
och talade språk men det har också funnits en tradition att krångla till det
i onödan för att slippa insyn.
Det påstås t ex att Newton hemlighöll sin fluxkalkyl (det som idag kallas
operatorkalkyl eller Laplace transform) och bara presenterade resultat som
ingen förstod hur han kommit fram till.
Det är viktigt att komma ihåg att teknik har en tradition av hemlighetsmakeri
bakom sig. Det förekommer till och med uttalanden som att det skulle finnas
svårförklarliga tekniska samband.
Man kan naturligtvis skriva en svårläst teknisk text på samma sätt som man kan
skriva en svårläst roman men när det gäller romanen inser alla att den är
svårläst för att författaren är en dålig berättare,inte för att handlingen är
svårbegriplig. Och teknik handlar också om vår verklighet med en handling som
aldrig är svårbegriplig.Om en teknisk text är svårläst kan det ha tre orsaker
Författaren är okunnig och tråkig
Författaren försöker göra sig märkvärdig genom att skriva obegripligheter
Författaren vänder sig till läsare som är vana vid ett annat språk
Sedan jag som barn lärde mig att acceptera att jorden är rund har jag aldrig
stött på en svårbegriplig naturvetenskaplig eller teknisk ide. Däremot har jag
sett en hel del undermåliga idepresentationer.
Koordinater
===========
Om vi skall kunna använda matematik för att precisera de önskemål vi vill
överföra till vår omgivning behöver vi någon metod att beskriva den
nuvarande omgivningen, den önskade omgivningen och den önskade förändringen.
Och det måste vara en beskrivning som inte innehåller några halvkvädna
visor. Vår omvärld kan inte läsa mellan raderna.
För att komma fram till en sådan beskrivning av omvärlden kan vi göra
tankeexperimentet att vi har en förenklad värld. Låt oss börja med en
värld som bara innehåller två punkter A och B. Det enda som kan ändras
i denna värld är avståndet mellan A och B (jag bortser här från frågan
om vad som menas med "avstånd" i en sådan värld). Vi tänker oss en linje
mellan A och B och karaktäriserar världen genom att ange avståndet
mellan A och B. Denna värld karaktäriseras alltså helt av ett enda tal
och vi kallar den därför för en endimensionell värld.
Om vi så lägger till en tredje punkt C kan den hamna på linjen d v s
hamna inom den endimensionella världen men den kan också hamna vid sidan
av linjen. Om den hamnar vid sidan av linjen behöver vi, förutom avståndet
till A (eller B), ange avståndet till linjen för att vi skall kunna ange
läget exakt. För varje punkt behöver vi nu två tal för att ange läget.
Vi kallar därför en sådan värld för tvådimensionell.
Vi brukar inte ange avståndet A till C och avståndet C till linjen utan
vi anger avståndet till linjen och projektionen på linjen av avståndet
A till C.
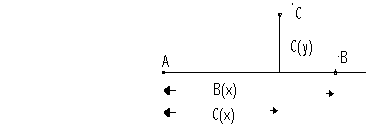 Fig 1
I fig 1 har punkten A koordinaterna 0,0 (om jag lägger origo i A).
Punkten B har koordinaterna B(x),0 och punkten C har koordinaterna
C(x),C(y).
En tvådimensionell värld kallar vi för en yta.
Om vi nu utökar vår värld med en fjärde punkt D kan denna falla i ytan
men det är också möjligt att den hamnar utanför ytan. Om den hamnar utanför
ytan anger vi dess läge genom att ange de två koordinaterna för punktens
projektion på ytan plus en tredje koordinat som anger avståndet till ytan.
För att ange läge i denna värld krävs alltså att man anger tre koordinater
och vi kallar en sådan värld tredimensionell.
Tre koordinater kan vi projicera på tre vinkelräta räta linjer som vi
kallar för koordinataxlar. Ett sådant koordinatsystem kallas för
cartesianskt.Det finns andra sätt att åstadkoma koordinatsystem. Man kan
t ex ange en sträcka och två vinklar eller använda system med krökta
koordinataxlar men tills vidare får det cartesianska systemet räcka.
Vad händer när vi lägger till en femte punkt E?Hittills har det för varje
ny punkt varit möjligt att lägga den utanför den etablerade världen så att
den gett en ny dimension. Gäller detta även för punkt E?
Vår hjärna har ett program som inte kan räkna med mer än tre vinkelräta
rätlinjiga axlar. Men betyder det att det inte kan finnas fler eller
betyder det bara att vi ser världen projicerad på ett treaxligt
koordinatsystem? Hur skall vi veta om det räcker med tre axlar?
Vi behöver ett kriterium som vi kan använda för att avgöra om ett
koordinatsystem är fullständigt eller inte.Ett sådant kriterium skulle
kunna formuleras på följande sätt:
Om två partiklar kan ha samtliga koordinater lika utan att de
växelverkar är koordinatsystemet ofullständigt.
Det är uppenbart att ett tredimensionellt koordinatsystem är
ofullständigt. Två bilar kan köra genom en korsning så att de i alla
avseenden har samma lägeskoordinater men om de gör det vid olika tidpunkt
finns ingen växelverkan mellan dem. Lägger vi då till tid som en fjärde
koordinataxel finner vi att om alla fyra koordinaterna sammanfaller
för bilarna får vi alltid en mycket påtaglig växelverkan mellan dem.
Ett koordinatsystem som beskriver en fyrdimensionell värld förefaller vara
fullständigt.
Man skulle kunna diskutera om t ex frekvens skulle kunna ses som en femte
dimension. Två signaler med olika frekvens kan ju samtidigt finnas på
samma antenn utan att störa varandra. Men detta beror på att etern och
antennen är praktiskt taget linjära så att summan av signalerna inte
innehåller något annat än det som fanns i de båda signalerna. Ersätter
vi antennen med ett olinjärt element, t ex en diod, ger växelverkan mellan
signalerna upphov till en ny signal som inte fanns i de ingående
signalerna. Vi behöver alltså ett olinjärt element för att se växelverkan
men att den inte syns med en linjär antenn motiverar inte att vi ser
frekvens som en femte dimension.
I princip kan varje ny punkt som avviker från omgivningen dyka upp i en
ny dimension. Antalet möjliga dimensioner är alltså antalet partiklar
minus ett. Att vår värld med alla dess partiklar ryms inom fyra dimensioner
eller åtminstone med framgång kan projiceras på fyra dimensioner, är ett av
de stora mysterierna.
Det påstås ibland att världen vid Big Bang skulle ha haft elva dimensioner
men jag har aldrig hittat någon vettig motivering för detta påstående
och jag betraktar därför detta, liksom hela Big Bang-iden, tills vidare som
Hokus Pokus eller snarare som Hoc est...
Vad är energi?
==============
Sedan urminnes tid har människan försökt förändra sin omgivning för att få
den att stämma med hennes önskemål. Sådan förändring kräver ansträngning och
vi kallar detta för arbete.
Förändring av omgivningen är i många fall det samma som att flytta föremål.
Om alla koordinater för alla partiklar är oförändrade har ju ingenting
ändrats. En förändring innebär alltså att några koordinater måste ändras
d v s att något måste förflyttas. Om vi vill flytta ett föremål trots att
det av någon anledning tar emot måste vi anstränga oss, d v s vi måste
uträtta ett arbete. I tekniska sammanhang studerar man endast denna typ
av arbete och för att skilja detta från andra former av arbete, t ex från
tankearbete, använder vi benämningen tekniskt arbete eller om det inte
finns risk för missförstånd enbart begreppet arbete.
Den ansträngning som krävs för att flytta ett föremål beror dels på hur
mycket man måste ta i för att rubba föremålet d v s på den kraft som
erfordras dels på hur långt man flyttar det. Vi säger att arbete är
produkten av kraft gånger väg.
För några hundra år sedan började man förstå att det fanns andra sätt
att åstadkomma arbete än via muskelarbete. Man använde t ex vind och
forsar. Så småningom lärde vi oss också att använda temperaturändringar
för att få gaser att ändra volym och därmed uträtta arbete.
Vi fann att alla förutsebara förändringar kunde omvandlas till nyttigt
arbete. Ju mer vi lärde oss om att omvandla olika förändringar till
arbete ju större blev behovet av ett begrepp och av måttenheter för
allt som kunde omvandlas till arbete. Vi började kalla allt som kunde
omvandlas till arbete för "energi".
Om vi har ett tillstånd som på något sätt avviker från det mest sannolika
kan vi förutse att detta kommer att förändras så att det närmar sig det
mest sannolika. En sådan avvikelse är alltså en potentiell förändring
d v s energi.
Att en förändring är förutsägbar innebär att vi kan beräkna dess storlek.
Men för sådana beräkningar behöver vi kvantitativa mått. Vi brukar då se
energi som en produkt av två mätbara storheter. Ofta gör vi den
uppdelningen så att den ena storheten kan betraktas som en mängdstorhet
(extensiv faktor) och den andra som en intensitetsfaktor (intensiv
faktor).
Energi är alltså ett kvantitativt mått på förutsägbar förändring.
Antag att en kula ligger på ett bord. Om kulan rullar över bordskanten
inträffar en förutsägbar förändring, kulan faller från bordet mot golvet.
Ju högre bordet är ju större är denna förutsägbara förändring och ju
tyngre kulan är ju större är förändringen. Vi säger att bordets höjd
gånger kulans tyngd är den förutsägbara förändringen som inträffar när
kulan faller från bordet, d v s bordets höjd gånger kulans tyngd är kulans
energi.
När vi talar om energianvändning menar vi att vi använder spontana förutsäg-
bara förändringar för att åstadkomma de förändringar vi önskar. Begreppet
"förutsägbarhet" är nära knutet till begreppet "användbarhet". Vill vi t ex
klyva ett vedträ försöker vi åstadkomma en situation där vi kan förutse att
vi får en förändring som resulterar i att vedträt klyvs. Vi sätter oss inte
och väntar på att slumpmässiga förändringar skall leda till att vedträt
spricker.
Med energikällor menar vi tillstånd som avviker från omgivningen på sådant sätt
att vi kan förutse att dessa avvikelser kommer att utjämnas.
Låt oss se på några exempel på avvikelser som vi anser användbara och avvikelser
som skulle kunna vara användbara.
Betrakta en avgränsad gasmängd, t ex en luftmassa. Låt oss först se på
molekylernas läge. Om medelvärdet av molekylernas avstånd till varandra
avviker från motsvarande medelvärde i omgivningen har vi en täthets-
avvikelse mellan gasmängden och omgivningen. Vi kan förutsäga att om
vi möjliggör utbyte med omgivningen kommer denna täthetsavvikelse att
utjämnas. Denna utjämning blir en förutsägbar förändring. Avvikelse i
medelavstånd betraktar vi som användbar energi.
Om molekylavståndets varians avviker från omgivningens kan vi förutsäga
att denna avvikelse kommer att utjämnas. Avvikelser i molekylavståndets
varians är alltså i princip användbara men vi känner ingen metod att
utnyttja dessa och betraktar dem därför inte som användbar energi.
Låt oss så se på tidsderivatan av läget, d v s på molekylhastigheten.
Om medelvärdet av molekylhastigheten avviker från motsvarande hastighet
i omgivningen har vi en vind som vi kan utnyttja. Vi kan t ex låta
hastighetsskillnaden utjämnas via en propeller på en vindsnurra. Utjämning
av skillnad i molekylernas medelhastighet betraktar vi alltså som
användbar energi.
Om molekylhastighetens varians avviker från motsvarande storhet i
omgivningen säger vi att vi har en temperaturavvikelse mot omgivningen.
Temperatur är ju molekylvikt gånger molekylhastighetens varians. På
1800-talet lärde vi oss att använda förutsägbara förändringar av
molekylhastighetens varians, d v s vi lärde oss att omvandla värme i
andra energiformer.
Avvikelser i medelvärde och varians för andra tidsderivatan av läget
borde också vara användbara. D v s avvikelser i medelvärde och varians
för molekylaccelerationen borde vara användbara. Men för andra tids-
derivatan har vi, lika lite som för högre derivator, någon praktisk
metod för energiomvandling.
Det är också så att ett tillstånd kan avvika från omgivningen på andra
sätt än de som karaktäriseras av medelvärde och varians. Det är inte
svårt att tänka sig osannolika fördelningar med samma medelvärde och
varians som omgivningen. Om en fördelning är osannolik kan vi förutsäga
att den spontant kommer att övergå till en mera sannolik. En sådan
fördelning är alltså användbar eftersom den ger en förutsägbar
förändring. Men frånsett ett fåtal osannolika tillstånd med avvikande
medelvärde och varians känner vi inte till praktiska metoder att
använda de osannolika tillstånd som omger oss. Och vi gör knappast
några försök att finna sådana metoder.
När vi pratar om energi brukar vi utgå från att vi skall använda
osannolikt stora avvikelser från medelvärde eller varians. Men för
ett tillstånd där avvikelserna är osannolikt små kan vi också förutsäga
hur tillståndet kommer att förändras. Här finns alltså en hel klass
"användbara" (i betydelsen förutsägbart föränderliga) tillstånd som
är lika stor som den dit alla våra kända energikällor hör men där vi
idag inte har någon aning om de kan användas praktiskt och i så fall
hur och till vad.
Att man kunde använda avvikelser i luftmolekylernas medelhastighet, d v s
vind, var känt sedan urminnes tid. Att segla med hjälp av vind är en
gammal konst. Att man även kan använda avvikelser i varians för luft-
molekylernas hastighet, d v s temperaturskillnader, för att driva maskiner
är en kunskap som bara är några få århundraden gammal. Det är naturligtvis
fullt tänkbart att vi om något århundrade betraktar användning av
avvikelser hos högre tidsderivator eller i fördelningsmått av högre
ordning som lika självklart som vi idag ser användning av värmemaskiner.
Att värme från brinnande olja skulle kunna driva en bil måste för 1700-
talets människor ha tett sig som helt otänkbart. Men trots det fanns det
de som försökte och gjorde detta möjligt att uppnå så småningom.
Vad är tid ?
============
Energi är förutsebara förändringar som vi genom förutsebarheten kan
utnyttja och omvandla enligt våra önskemål. Men vi behöver också ett
begrepp för och ett mått på alla förändringar som påverkar vår omgivning.
Summan av alla förändringar kallar vi tid.
Energi och tid är alltså mycket nära besläktade begrepp.Båda är
kvantitativa förändringsmått.
När vi använder energi använder vi en del av den förutsägbara delen av
de förändringar som utgör tidsflödet.
Varje märkbar förändring är en händelse och varje händelse är ett
tidsinkrement. I princip skulle vi kunna mäta tid i antal tidsinkrement
men det skulle bli ohanterligt stora tal för praktiskt bruk och vi brukar
därför använda enheten sekund som är ett visst (stort) antal tidsinkrement
eller år som är ännu fler tidsinkrement.
Händelser inträffar slumpvis men händelser kan vara kopplade så att
händelse A kan öka sannolikheten för händelse B.Om man kör en bil innebär
händelsen att framänden rör sig i förhållande till vägen att sannolikheten
för händelsen att bakänden skall röra sig i förhållande till vägen ökar.
Och det finns en kedja av kopplade händelser som via gasspjället,
förbränning i motorn och vridning av drivhjulen höjer sannolikheten att
bilen skall röra sig på vägen.
Ett sätt att beskriva tidsflödet kan vara att likna det vid lotterier.
Antag att man har 106 lotterier med vardera 106 lotter.
Varje lott motsvarar en potentiell händelse och varje vinst motsvarar att
händelsen inträffar. Om varje lotteri har 100 vinster är sannolikheten
att vinna i en dragning om man vet att man har en lott i rätt lotteri
1/104. Om man inte vet vilket lotteri man har en lott i blir sannolikheten
för vinst 1/1010. Koppling av händelser motsvaras av koppling av lotter
genom att de tillhör samma lotteri.
Om jag köper 103 lotter blir sannolikheten för vinst i varje dragning
1/107. När jag har fått 10 vinster kan jag alltså dra slutsatsen att det
har förekommit 108 dragningar vilket innebär att 1010 vinster
har fallit ut. Genom att följa vinstutfallet på min lilla lottbunt kan jag alltså
dra slutsatser om totala vinstutfallet i alla lotterier.
På motsvarande sätt kan vi avgränsa en grupp potentiella händelser och
genom att se hur många av dem som inträffar kan vi dra slutsatser om hur
många händelser som inträffar i hela universum. Vi kan t ex avgränsa en
svängande pendel, en oro, en kvartskristall eller en grupp cesiumatomer.
Kring detta avgränsade system kan vi bygga en klocka som mäter totala
antalet händelser i universum.
Det antal händelser som klockan mäter är en viss fast andel av totala
antalet händelser. För att få totala antalet händelser skall vi alltså
multiplicera det antal som klockan mätt upp med en konstant. Storleken
på denna konstant vet vi inte. Vi vet bara att det är en konstant.
Vi kan alltså inte fastställa konstantens värde men vi kan övertyga oss
om att det verkligen är fråga om en konstant.
Om våra klockor verkligen mäter totala antalet händelser i universum
skall alla klockor ange samma värde. Det är svårt att veta hur vi har
avgränsat våra klockor d v s att veta hur många lotter vi har köpt men
om de kan gå utan koppling till ovidkommande händelser skall det vara
möjligt att sätta på dem urverk med sådan utväxling att de går lika
fort. Och har vi en gång fått dem att gå lika fort skall de fortsätta
att göra det.
Vi finner då, mycket riktigt, att ju bättre vi kan avgränsa våra klockor
från koppling till ovidkommande händelser ju bättre går de. En svängande
pendel påverkas av vibrationer i upphängningen, temperaturvariationer,
luftrörelser mm. Men trots det visar olika pendelur påtaglig
överensstämmelse.
För en grupp cesiumatomer är möjligheten att undvika inverkan av
ovidkommande händelser betydligt bättre än för en pendel. Det är också
möjligt att bygga atomur som visar mycket god överensstämmelse.
Vad vill vi egentligen?
=======================
Teknik är att,via någon form av utväxling,anpassa extensiv och intensiv
faktor till vad vi har tillgång till.Till exempel att via ett spett
åstadkomma ökad kraft för att rubba en sten.
Teknik är också att utnyttja förutsägbara förändringar i vår omgivning till
att motsvara våra önskemål.Till exempel att använda den förutsägbara
förändringen när ett vedträ brinner genom att ta in det och tända det i
spisen när det är kallt i rummet.
Och teknik är också att analysera våra önskemål så att vi slipper anstränga
oss för sådant som vi inte är intresserade av.
Om Gustav III hade bestämt sig för att satsa på att kunna meddela sig
snabbare med Göteborg hade man hamnat i att bygga bättre vägar, att bygga
gästgivargårdar utefter vägarna och att avla fram bättre hästar. Vi hade
fått kurirer som på löddriga springare sprängde fram genom landet med brev
i postväskan.
När järnvägen kom fick vi, på köpet, snabbare brevbefordran.
Men den stora förändringen kom när man insåg att det handlade om att
överföra brevets innehåll, inte själva brevet. I vissa länder byggde man
optiska telegrafer där man från torn till torn överförde signaler genom
att en operatör i ett torn kunde se hur operatören i föregående torn
ställde sina signalskivor och så upprepa dessa inställningar i sitt torn
så att de kunde ses från nästa torn.
Vi ser den optiska telegrafen som ett monster av personalkrävande
ineffektivitet men när alternativet var kurirer ute på vägarna innebar
den en enorm besparing både av arbetskraft och överföringstid.
Med en elektrisk ledning mellan tornen kunde man signalera med större
tornavstånd. Och genom att man insåg att varje meddelande kan brytas ner
i binära bitar kunde man med morse-kod signalera via en enda tråd (eller
ett trådpar).
Genom att analysera vad vi egentligen önskade har vi alltså insett att
brevet inte var nödvändigt och att budskapet kunde reduceras till binära
bitar. Det har fört oss långt bort från hästavel och medfört att vi idag
tar för givet att överföringstid mellan Stockholm och Göteborg räknas i
millisekunder, inte i dagar.
När jag var liten, i mitten av 1900-talet, var det fortfarande vanligt
att man på vintrarna sågade upp is på sjöarna. Isblocken körde man hem
och lade i sågspånshögar så att man hade tillgång till is under sommaren.
I städerna använde man isskåp där maten hölls sval av is som man köpte av
en iskarl som åkte runt och sålde is. Många iskarlar trodde nog att de
faktiskt sålde is men en närmare analys av problemet ledde till insikten
att de sålde kyla och därmed till frågan om vilka möjligheter det fanns
att åstadkomma kyla. Och resultatet av den insikten blev Electroluxkylskåpet
och kompressorkylskåpet.
När man började bygga drivande och drivna maskiner behövde man göra en
uppdelning så att de som arbetade med att utveckla drivande maskiner kunde
arbeta utan att nödvändigtvis veta vad maskinen skulle driva och att de som
utvecklade drivna maskiner kunde arbeta utan att vara låsta till en viss
drivmaskin. Detta löste man med den roterande axeln som standardiserat
kopplingselement. En drivande maskin skulle alltid avslutas med en roterande
axel och en driven maskin skulle alltid försörjas via en roterande axel.
Sedan dess har elektrisk kraftöverföring utvecklats från att vara ett
alternativ för överföringar på några kilometer till att bli konkurenskraftig
på allt kortare överföringar. Möjligheten att styra strömmar med
halvledarteknik har idag medfört att elektrisk kraftöverföring mycket
ofta är konkurenskraftig även på de korta avstånd som den roterande axeln
använts för. Ett exempel som just nu är aktuellt är att ersätta
kardanaxelöverföringen i bilar med elektrisk kraftöverföring.
Insikten att den roterande axeln kan ersättas med andra kopplingselement,
t ex elektrisk, pneumatisk eller hydraulisk överföring, kommer att öppna
många av de låsningar som den roterande axeln medfört, t ex begränsningar
i rörelsemönster hos en kolv med vevstake och sinusformens dominerande
ställning inom elteknik.
Som exempel på undermålig teknik i dagens samhälle kan man nämna att vi
flyttar drygt ett ton bil för att flytta 80 kg människa och än värre att
vi inom kollektivtrafiken ofta flyttar tomma bussar på tiotals ton utan
att uträtta något önskat transportarbete över huvud taget.
Ett annat exempel är framdrivning av båtar. Vi utgår då från en fram- och
återgående kolv. Denna kolvrörelse omvandlar vi via ett vevparti till
rotation. Rotationen överför vi till en propeller som åstadkommer vatten-
rotation och framdrivning. För tändning och för försörjning av hjälpsystem
har vi också vanligtvis någon typ av elgenerator. En gång i tiden motiverades
övergången till rotation av att man använde svänghjul för att driva motorns
ickedrivande takter. Men med dagens magnetmaterial och halvledarteknik kan
man åstadkomma detta med elektrisk drivning vilket skulle innebära att man
slipper hela vevpartiet, alla problem med propelleraxelgenomföringar och alla
förluster i form av vattenrotation. Man kan i stället låta den fram- och
återgående kolven verka direkt mot vattnet.
De första och viktigaste frågorna som man alltid måste ställa sig vid
teknisk utveckling är alltså "Vad är önskat resultat?" och "Finns det
något enklare sätt att uppnå detta?".
Det finns en vandringssägen om hur man inom NASA drev ett projekt med
syfte att ta fram en lättare rakapparat som astronauterna skulle kunna
ha vid längre resor. Projektet pågick tills en av teknikerna gick ner
till butiken på hörnet och köpte en rakhyvel.
Hastighet
=========
Jag träffade en gång i tiden en pedagog som sa:
"När eleverna kommer till skolan vet de mycket väl vad hastighet är. Så
inför vi begreppet hastighet som kvoten mellan väg och tid och efter det
begriper de ingenting."
För att krångla till det ytterligare skulle jag vilja påstå att hastighet
är ett mått på hur stor andel av totala antalet händelser i universum som
flyttar en av de punkter som jag för tillfället är intresserad av i en viss
riktning.
Och så gäller det att reda ut det på ett begripligt sätt.
Betrakta en bil som kör på en väg. Lägg in ett koordinatsystem på sådant
sätt att lägeskoordinaterna för punkter i vägen förblir i stort sett
konstanta. När bilen fått upp farten kommer lägeskoordinaterna för en
partikel i bilen att ändras. Och denna partikel är kopplad till övriga
partiklar i bilen på sådant sätt att sannolikheten är stor att även
dessas koordinater skall ändras på liknande sätt.
Och varje gång en händelse inträffar i universum ökar tiden ett tids-
inkrement.
Om vi läser av lägeskoordinaterna för en partikel i bilen,väntar tills
tiden ökat med ett visst antal händelser (t ex en sekund) och därefter
på nytt läser av lägeskoordinaterna för partikeln får vi alltså veta hur
mycket partikelns läge ändrats under det att ett visst antal händelser
inträffat i universum. Men minsta detekterbara lägesförändring är en
händelse och att vi får veta hur mycket läget ändrats betyder alltså
att vi får veta hur många detekterbara lägesförändringar i rörelse-
riktningen partikeln gjort d v s hur många av alla händelser som inträffat
i universum som avsåg förflyttning av vår partikel i rörelseriktningen.
Om vi dividerar detta antal händelser med totala antalet händelser d v s
om vi dividerar lägesändringen för vår partikel med den tid som läges-
förändringen tagit får vi det som vi brukar kalla hastighet.
Vad jag gör när jag trampar ner gaspedalen i bilen är alltså att jag
försöker få en större andel av alla de händelser som inträffar i
universum att handla om att bilens läge på vägen ändras.
Om bilen flyttar sig sträckan s på tiden τ blir hastigheten v där
v = s/τ
Men om jag trampar på gasen ökar hastigheten. Om jag beräknar hastigheten
som s/τ får jag medelvärdet av hastigheten under tiden τ. Ibland är det vad
jag vill ha men ibland är jag mer intresserad av att veta hur stor
hastighet jag uppnått vid slutet av tiden τ (eller av något annat).
Hur beräknar man hastighet när den inte är konstant under mättiden?
Låt oss börja med att se på det enkla fallet att hastigheten är
proportionell mot tiden.Vi kan då skriva
v = a τ
där proportionalitetskonstanten a kallas för accelerationen.
Hur långt kommer ett föremål som från hastigheten noll accelererar med
accelerationen a under tiden τ?
Efter tiden τ är hastigheten v = a τ men medelhastigheten under tiden τ
blir hälften så stor d v s
v = a τ/2
medel
och sträckan s som föremålet tillryggalägger blir
s = v τ = a τ2 /2
medel
Men varför är det intressant att se på fallet med konstant acceleration?
Är det bara för att det är lätt att räkna på eller är det för att sådant
förekommer i verkligheten?
Om man påverkar ett föremål med konstant kraft får man faktiskt (bortsett
från luftmotstånd,friktion o dyl) konstant acceleration. Kraften F på ett
föremål med massan m ger accelerationen a enligt
F = m a
Och ett vanligt fall där man har konstant kraft är vid fallrörelser. Jordens
dragningskraft påverkar ett föremål vid jordytan med en kraft som är
praktiskt taget proportionell mot föremålets massa. När vi släpper ett
föremål och låter det falla fritt blir alltså accelerationen alltid densamma.
Vi får för fritt fall
a = 9,81 m/s2
För denna acceleration används ofta symbolen g.
Parametertid och koordinattid
=============================
Vi tänker oss en observatör som bara kan tänka i två dimensioner. Han ser
alltså världen projicerad på en yta på samma sätt som vi ser den med ett
öga eller när vi avbildar den med en kamera.
Om någon partikel ändrar höjd över denna yta förändras världen men det är
inte säkert att det märks i hans projektion. Indirekt kan han upptäcka
förändringen t ex genom att han flyttar sig så att partikelprojektionen
ändras. Han kan alltså ana sig till att hans bild är ofullständig och att
han bör ange denna typ av förändring genom att lägga till en tredje
koordinataxel.
På liknande sätt kan vi ana oss till att vi bör lägga till en tidsaxel
till vårt treaxliga rumssystem.
Om vi befinner oss i ett slutet rum,som vi kan kalla vårt observationsrum,
kan vi göra tankeexperimentet att vi bestämmer koordinaterna för alla
partiklar i rummet. Om vi så gör om bestämningen och finner att samtliga
koordinater är oförändrade är då allt oförändrat?
Nej det kan vi inte påstå för det kan ju ha inträffat händelser som förändrat
rummet i sin helhet i förhållande till världen i övrigt. För att ange det
behöver vi någon koordinataxel där vi kan avsätta observationsrummets läge
i förhållande till världen i övrigt. Vi kan kalla denna koordinat för
koordinattid.
Vi får då två tidsbegrepp som vi kan kalla
Parametertid
Koordinattid
Parametertid anger antalet händelser i universum oavsett var de inträffat.
Så snart någon partikel i universum ändrar läge så mycket att det är
detekterbart går alltså parametertiden ett tidsinkrement.
Koordinattiden går ett tidsinkrement varje gång en detekterbar händelse
inträffar utanför observationsrummet. En händelse som inträffar i
observationsrummet innebär att någon eller några rumskoordinater ändras
i observationsrummet. En händelse som inträffar utanför observationsrummet
innebär att koordinattiden ökar.
Antag att vi betraktar uppskjutning av en bemannad raket. Vi kan då lägga
x-axeln i raketens färdriktnig och strunta i y- och z-axlarna. Vi kan då
beskriva vad som händer i ett tvåaxligt koordinatsystem med en rumsaxel
(x-axeln) och en tidsaxel (koordinattid).
För oss är raketen en del av observationsrummet som ändrar läge i förhållande
till resten av observationsrummet. För besättningen ombord på raketen däremot
är raketens kontrollrum observationsrummet där,i stort sett allt står stilla.
Vi har lagt vår x-axel och vår axel för koordinattid så att huvuddelen av
vår omgivning har konstant x-koordinat medan raketens x-koordinat ökar.
Besättningen på raketen däremot lägger sin x-axel och sin axel för
koordinattid så att det mesta i raketen har konstant x-koordinat.
När raketen startar accelererar den men låt oss göra tankeexperinmentet att
den slår av motorn efter en stund och går med konstant hastighet. Dess bana
i vårt tvåaxliga koordinatsystem blir då en rät linje. Och besättningen på
raketen lägger sin axel för koordinattid längs denna räta linje. Raketens
hastighet innebär alltså att besättningens koordinatsystem vrids vinkeln
α i förhållande till vårt koordinatsystem. Och om vi mäter längd och
tid i samma enhet (t ex både längd och tid i meter eller både längd och tid
i sekunder) blir raketens hastighet sin α om vi använder parametertid
eller tan α om vi använder koordinattid.
Fig 1
I fig 1 har punkten A koordinaterna 0,0 (om jag lägger origo i A).
Punkten B har koordinaterna B(x),0 och punkten C har koordinaterna
C(x),C(y).
En tvådimensionell värld kallar vi för en yta.
Om vi nu utökar vår värld med en fjärde punkt D kan denna falla i ytan
men det är också möjligt att den hamnar utanför ytan. Om den hamnar utanför
ytan anger vi dess läge genom att ange de två koordinaterna för punktens
projektion på ytan plus en tredje koordinat som anger avståndet till ytan.
För att ange läge i denna värld krävs alltså att man anger tre koordinater
och vi kallar en sådan värld tredimensionell.
Tre koordinater kan vi projicera på tre vinkelräta räta linjer som vi
kallar för koordinataxlar. Ett sådant koordinatsystem kallas för
cartesianskt.Det finns andra sätt att åstadkoma koordinatsystem. Man kan
t ex ange en sträcka och två vinklar eller använda system med krökta
koordinataxlar men tills vidare får det cartesianska systemet räcka.
Vad händer när vi lägger till en femte punkt E?Hittills har det för varje
ny punkt varit möjligt att lägga den utanför den etablerade världen så att
den gett en ny dimension. Gäller detta även för punkt E?
Vår hjärna har ett program som inte kan räkna med mer än tre vinkelräta
rätlinjiga axlar. Men betyder det att det inte kan finnas fler eller
betyder det bara att vi ser världen projicerad på ett treaxligt
koordinatsystem? Hur skall vi veta om det räcker med tre axlar?
Vi behöver ett kriterium som vi kan använda för att avgöra om ett
koordinatsystem är fullständigt eller inte.Ett sådant kriterium skulle
kunna formuleras på följande sätt:
Om två partiklar kan ha samtliga koordinater lika utan att de
växelverkar är koordinatsystemet ofullständigt.
Det är uppenbart att ett tredimensionellt koordinatsystem är
ofullständigt. Två bilar kan köra genom en korsning så att de i alla
avseenden har samma lägeskoordinater men om de gör det vid olika tidpunkt
finns ingen växelverkan mellan dem. Lägger vi då till tid som en fjärde
koordinataxel finner vi att om alla fyra koordinaterna sammanfaller
för bilarna får vi alltid en mycket påtaglig växelverkan mellan dem.
Ett koordinatsystem som beskriver en fyrdimensionell värld förefaller vara
fullständigt.
Man skulle kunna diskutera om t ex frekvens skulle kunna ses som en femte
dimension. Två signaler med olika frekvens kan ju samtidigt finnas på
samma antenn utan att störa varandra. Men detta beror på att etern och
antennen är praktiskt taget linjära så att summan av signalerna inte
innehåller något annat än det som fanns i de båda signalerna. Ersätter
vi antennen med ett olinjärt element, t ex en diod, ger växelverkan mellan
signalerna upphov till en ny signal som inte fanns i de ingående
signalerna. Vi behöver alltså ett olinjärt element för att se växelverkan
men att den inte syns med en linjär antenn motiverar inte att vi ser
frekvens som en femte dimension.
I princip kan varje ny punkt som avviker från omgivningen dyka upp i en
ny dimension. Antalet möjliga dimensioner är alltså antalet partiklar
minus ett. Att vår värld med alla dess partiklar ryms inom fyra dimensioner
eller åtminstone med framgång kan projiceras på fyra dimensioner, är ett av
de stora mysterierna.
Det påstås ibland att världen vid Big Bang skulle ha haft elva dimensioner
men jag har aldrig hittat någon vettig motivering för detta påstående
och jag betraktar därför detta, liksom hela Big Bang-iden, tills vidare som
Hokus Pokus eller snarare som Hoc est...
Vad är energi?
==============
Sedan urminnes tid har människan försökt förändra sin omgivning för att få
den att stämma med hennes önskemål. Sådan förändring kräver ansträngning och
vi kallar detta för arbete.
Förändring av omgivningen är i många fall det samma som att flytta föremål.
Om alla koordinater för alla partiklar är oförändrade har ju ingenting
ändrats. En förändring innebär alltså att några koordinater måste ändras
d v s att något måste förflyttas. Om vi vill flytta ett föremål trots att
det av någon anledning tar emot måste vi anstränga oss, d v s vi måste
uträtta ett arbete. I tekniska sammanhang studerar man endast denna typ
av arbete och för att skilja detta från andra former av arbete, t ex från
tankearbete, använder vi benämningen tekniskt arbete eller om det inte
finns risk för missförstånd enbart begreppet arbete.
Den ansträngning som krävs för att flytta ett föremål beror dels på hur
mycket man måste ta i för att rubba föremålet d v s på den kraft som
erfordras dels på hur långt man flyttar det. Vi säger att arbete är
produkten av kraft gånger väg.
För några hundra år sedan började man förstå att det fanns andra sätt
att åstadkomma arbete än via muskelarbete. Man använde t ex vind och
forsar. Så småningom lärde vi oss också att använda temperaturändringar
för att få gaser att ändra volym och därmed uträtta arbete.
Vi fann att alla förutsebara förändringar kunde omvandlas till nyttigt
arbete. Ju mer vi lärde oss om att omvandla olika förändringar till
arbete ju större blev behovet av ett begrepp och av måttenheter för
allt som kunde omvandlas till arbete. Vi började kalla allt som kunde
omvandlas till arbete för "energi".
Om vi har ett tillstånd som på något sätt avviker från det mest sannolika
kan vi förutse att detta kommer att förändras så att det närmar sig det
mest sannolika. En sådan avvikelse är alltså en potentiell förändring
d v s energi.
Att en förändring är förutsägbar innebär att vi kan beräkna dess storlek.
Men för sådana beräkningar behöver vi kvantitativa mått. Vi brukar då se
energi som en produkt av två mätbara storheter. Ofta gör vi den
uppdelningen så att den ena storheten kan betraktas som en mängdstorhet
(extensiv faktor) och den andra som en intensitetsfaktor (intensiv
faktor).
Energi är alltså ett kvantitativt mått på förutsägbar förändring.
Antag att en kula ligger på ett bord. Om kulan rullar över bordskanten
inträffar en förutsägbar förändring, kulan faller från bordet mot golvet.
Ju högre bordet är ju större är denna förutsägbara förändring och ju
tyngre kulan är ju större är förändringen. Vi säger att bordets höjd
gånger kulans tyngd är den förutsägbara förändringen som inträffar när
kulan faller från bordet, d v s bordets höjd gånger kulans tyngd är kulans
energi.
När vi talar om energianvändning menar vi att vi använder spontana förutsäg-
bara förändringar för att åstadkomma de förändringar vi önskar. Begreppet
"förutsägbarhet" är nära knutet till begreppet "användbarhet". Vill vi t ex
klyva ett vedträ försöker vi åstadkomma en situation där vi kan förutse att
vi får en förändring som resulterar i att vedträt klyvs. Vi sätter oss inte
och väntar på att slumpmässiga förändringar skall leda till att vedträt
spricker.
Med energikällor menar vi tillstånd som avviker från omgivningen på sådant sätt
att vi kan förutse att dessa avvikelser kommer att utjämnas.
Låt oss se på några exempel på avvikelser som vi anser användbara och avvikelser
som skulle kunna vara användbara.
Betrakta en avgränsad gasmängd, t ex en luftmassa. Låt oss först se på
molekylernas läge. Om medelvärdet av molekylernas avstånd till varandra
avviker från motsvarande medelvärde i omgivningen har vi en täthets-
avvikelse mellan gasmängden och omgivningen. Vi kan förutsäga att om
vi möjliggör utbyte med omgivningen kommer denna täthetsavvikelse att
utjämnas. Denna utjämning blir en förutsägbar förändring. Avvikelse i
medelavstånd betraktar vi som användbar energi.
Om molekylavståndets varians avviker från omgivningens kan vi förutsäga
att denna avvikelse kommer att utjämnas. Avvikelser i molekylavståndets
varians är alltså i princip användbara men vi känner ingen metod att
utnyttja dessa och betraktar dem därför inte som användbar energi.
Låt oss så se på tidsderivatan av läget, d v s på molekylhastigheten.
Om medelvärdet av molekylhastigheten avviker från motsvarande hastighet
i omgivningen har vi en vind som vi kan utnyttja. Vi kan t ex låta
hastighetsskillnaden utjämnas via en propeller på en vindsnurra. Utjämning
av skillnad i molekylernas medelhastighet betraktar vi alltså som
användbar energi.
Om molekylhastighetens varians avviker från motsvarande storhet i
omgivningen säger vi att vi har en temperaturavvikelse mot omgivningen.
Temperatur är ju molekylvikt gånger molekylhastighetens varians. På
1800-talet lärde vi oss att använda förutsägbara förändringar av
molekylhastighetens varians, d v s vi lärde oss att omvandla värme i
andra energiformer.
Avvikelser i medelvärde och varians för andra tidsderivatan av läget
borde också vara användbara. D v s avvikelser i medelvärde och varians
för molekylaccelerationen borde vara användbara. Men för andra tids-
derivatan har vi, lika lite som för högre derivator, någon praktisk
metod för energiomvandling.
Det är också så att ett tillstånd kan avvika från omgivningen på andra
sätt än de som karaktäriseras av medelvärde och varians. Det är inte
svårt att tänka sig osannolika fördelningar med samma medelvärde och
varians som omgivningen. Om en fördelning är osannolik kan vi förutsäga
att den spontant kommer att övergå till en mera sannolik. En sådan
fördelning är alltså användbar eftersom den ger en förutsägbar
förändring. Men frånsett ett fåtal osannolika tillstånd med avvikande
medelvärde och varians känner vi inte till praktiska metoder att
använda de osannolika tillstånd som omger oss. Och vi gör knappast
några försök att finna sådana metoder.
När vi pratar om energi brukar vi utgå från att vi skall använda
osannolikt stora avvikelser från medelvärde eller varians. Men för
ett tillstånd där avvikelserna är osannolikt små kan vi också förutsäga
hur tillståndet kommer att förändras. Här finns alltså en hel klass
"användbara" (i betydelsen förutsägbart föränderliga) tillstånd som
är lika stor som den dit alla våra kända energikällor hör men där vi
idag inte har någon aning om de kan användas praktiskt och i så fall
hur och till vad.
Att man kunde använda avvikelser i luftmolekylernas medelhastighet, d v s
vind, var känt sedan urminnes tid. Att segla med hjälp av vind är en
gammal konst. Att man även kan använda avvikelser i varians för luft-
molekylernas hastighet, d v s temperaturskillnader, för att driva maskiner
är en kunskap som bara är några få århundraden gammal. Det är naturligtvis
fullt tänkbart att vi om något århundrade betraktar användning av
avvikelser hos högre tidsderivator eller i fördelningsmått av högre
ordning som lika självklart som vi idag ser användning av värmemaskiner.
Att värme från brinnande olja skulle kunna driva en bil måste för 1700-
talets människor ha tett sig som helt otänkbart. Men trots det fanns det
de som försökte och gjorde detta möjligt att uppnå så småningom.
Vad är tid ?
============
Energi är förutsebara förändringar som vi genom förutsebarheten kan
utnyttja och omvandla enligt våra önskemål. Men vi behöver också ett
begrepp för och ett mått på alla förändringar som påverkar vår omgivning.
Summan av alla förändringar kallar vi tid.
Energi och tid är alltså mycket nära besläktade begrepp.Båda är
kvantitativa förändringsmått.
När vi använder energi använder vi en del av den förutsägbara delen av
de förändringar som utgör tidsflödet.
Varje märkbar förändring är en händelse och varje händelse är ett
tidsinkrement. I princip skulle vi kunna mäta tid i antal tidsinkrement
men det skulle bli ohanterligt stora tal för praktiskt bruk och vi brukar
därför använda enheten sekund som är ett visst (stort) antal tidsinkrement
eller år som är ännu fler tidsinkrement.
Händelser inträffar slumpvis men händelser kan vara kopplade så att
händelse A kan öka sannolikheten för händelse B.Om man kör en bil innebär
händelsen att framänden rör sig i förhållande till vägen att sannolikheten
för händelsen att bakänden skall röra sig i förhållande till vägen ökar.
Och det finns en kedja av kopplade händelser som via gasspjället,
förbränning i motorn och vridning av drivhjulen höjer sannolikheten att
bilen skall röra sig på vägen.
Ett sätt att beskriva tidsflödet kan vara att likna det vid lotterier.
Antag att man har 106 lotterier med vardera 106 lotter.
Varje lott motsvarar en potentiell händelse och varje vinst motsvarar att
händelsen inträffar. Om varje lotteri har 100 vinster är sannolikheten
att vinna i en dragning om man vet att man har en lott i rätt lotteri
1/104. Om man inte vet vilket lotteri man har en lott i blir sannolikheten
för vinst 1/1010. Koppling av händelser motsvaras av koppling av lotter
genom att de tillhör samma lotteri.
Om jag köper 103 lotter blir sannolikheten för vinst i varje dragning
1/107. När jag har fått 10 vinster kan jag alltså dra slutsatsen att det
har förekommit 108 dragningar vilket innebär att 1010 vinster
har fallit ut. Genom att följa vinstutfallet på min lilla lottbunt kan jag alltså
dra slutsatser om totala vinstutfallet i alla lotterier.
På motsvarande sätt kan vi avgränsa en grupp potentiella händelser och
genom att se hur många av dem som inträffar kan vi dra slutsatser om hur
många händelser som inträffar i hela universum. Vi kan t ex avgränsa en
svängande pendel, en oro, en kvartskristall eller en grupp cesiumatomer.
Kring detta avgränsade system kan vi bygga en klocka som mäter totala
antalet händelser i universum.
Det antal händelser som klockan mäter är en viss fast andel av totala
antalet händelser. För att få totala antalet händelser skall vi alltså
multiplicera det antal som klockan mätt upp med en konstant. Storleken
på denna konstant vet vi inte. Vi vet bara att det är en konstant.
Vi kan alltså inte fastställa konstantens värde men vi kan övertyga oss
om att det verkligen är fråga om en konstant.
Om våra klockor verkligen mäter totala antalet händelser i universum
skall alla klockor ange samma värde. Det är svårt att veta hur vi har
avgränsat våra klockor d v s att veta hur många lotter vi har köpt men
om de kan gå utan koppling till ovidkommande händelser skall det vara
möjligt att sätta på dem urverk med sådan utväxling att de går lika
fort. Och har vi en gång fått dem att gå lika fort skall de fortsätta
att göra det.
Vi finner då, mycket riktigt, att ju bättre vi kan avgränsa våra klockor
från koppling till ovidkommande händelser ju bättre går de. En svängande
pendel påverkas av vibrationer i upphängningen, temperaturvariationer,
luftrörelser mm. Men trots det visar olika pendelur påtaglig
överensstämmelse.
För en grupp cesiumatomer är möjligheten att undvika inverkan av
ovidkommande händelser betydligt bättre än för en pendel. Det är också
möjligt att bygga atomur som visar mycket god överensstämmelse.
Vad vill vi egentligen?
=======================
Teknik är att,via någon form av utväxling,anpassa extensiv och intensiv
faktor till vad vi har tillgång till.Till exempel att via ett spett
åstadkomma ökad kraft för att rubba en sten.
Teknik är också att utnyttja förutsägbara förändringar i vår omgivning till
att motsvara våra önskemål.Till exempel att använda den förutsägbara
förändringen när ett vedträ brinner genom att ta in det och tända det i
spisen när det är kallt i rummet.
Och teknik är också att analysera våra önskemål så att vi slipper anstränga
oss för sådant som vi inte är intresserade av.
Om Gustav III hade bestämt sig för att satsa på att kunna meddela sig
snabbare med Göteborg hade man hamnat i att bygga bättre vägar, att bygga
gästgivargårdar utefter vägarna och att avla fram bättre hästar. Vi hade
fått kurirer som på löddriga springare sprängde fram genom landet med brev
i postväskan.
När järnvägen kom fick vi, på köpet, snabbare brevbefordran.
Men den stora förändringen kom när man insåg att det handlade om att
överföra brevets innehåll, inte själva brevet. I vissa länder byggde man
optiska telegrafer där man från torn till torn överförde signaler genom
att en operatör i ett torn kunde se hur operatören i föregående torn
ställde sina signalskivor och så upprepa dessa inställningar i sitt torn
så att de kunde ses från nästa torn.
Vi ser den optiska telegrafen som ett monster av personalkrävande
ineffektivitet men när alternativet var kurirer ute på vägarna innebar
den en enorm besparing både av arbetskraft och överföringstid.
Med en elektrisk ledning mellan tornen kunde man signalera med större
tornavstånd. Och genom att man insåg att varje meddelande kan brytas ner
i binära bitar kunde man med morse-kod signalera via en enda tråd (eller
ett trådpar).
Genom att analysera vad vi egentligen önskade har vi alltså insett att
brevet inte var nödvändigt och att budskapet kunde reduceras till binära
bitar. Det har fört oss långt bort från hästavel och medfört att vi idag
tar för givet att överföringstid mellan Stockholm och Göteborg räknas i
millisekunder, inte i dagar.
När jag var liten, i mitten av 1900-talet, var det fortfarande vanligt
att man på vintrarna sågade upp is på sjöarna. Isblocken körde man hem
och lade i sågspånshögar så att man hade tillgång till is under sommaren.
I städerna använde man isskåp där maten hölls sval av is som man köpte av
en iskarl som åkte runt och sålde is. Många iskarlar trodde nog att de
faktiskt sålde is men en närmare analys av problemet ledde till insikten
att de sålde kyla och därmed till frågan om vilka möjligheter det fanns
att åstadkomma kyla. Och resultatet av den insikten blev Electroluxkylskåpet
och kompressorkylskåpet.
När man började bygga drivande och drivna maskiner behövde man göra en
uppdelning så att de som arbetade med att utveckla drivande maskiner kunde
arbeta utan att nödvändigtvis veta vad maskinen skulle driva och att de som
utvecklade drivna maskiner kunde arbeta utan att vara låsta till en viss
drivmaskin. Detta löste man med den roterande axeln som standardiserat
kopplingselement. En drivande maskin skulle alltid avslutas med en roterande
axel och en driven maskin skulle alltid försörjas via en roterande axel.
Sedan dess har elektrisk kraftöverföring utvecklats från att vara ett
alternativ för överföringar på några kilometer till att bli konkurenskraftig
på allt kortare överföringar. Möjligheten att styra strömmar med
halvledarteknik har idag medfört att elektrisk kraftöverföring mycket
ofta är konkurenskraftig även på de korta avstånd som den roterande axeln
använts för. Ett exempel som just nu är aktuellt är att ersätta
kardanaxelöverföringen i bilar med elektrisk kraftöverföring.
Insikten att den roterande axeln kan ersättas med andra kopplingselement,
t ex elektrisk, pneumatisk eller hydraulisk överföring, kommer att öppna
många av de låsningar som den roterande axeln medfört, t ex begränsningar
i rörelsemönster hos en kolv med vevstake och sinusformens dominerande
ställning inom elteknik.
Som exempel på undermålig teknik i dagens samhälle kan man nämna att vi
flyttar drygt ett ton bil för att flytta 80 kg människa och än värre att
vi inom kollektivtrafiken ofta flyttar tomma bussar på tiotals ton utan
att uträtta något önskat transportarbete över huvud taget.
Ett annat exempel är framdrivning av båtar. Vi utgår då från en fram- och
återgående kolv. Denna kolvrörelse omvandlar vi via ett vevparti till
rotation. Rotationen överför vi till en propeller som åstadkommer vatten-
rotation och framdrivning. För tändning och för försörjning av hjälpsystem
har vi också vanligtvis någon typ av elgenerator. En gång i tiden motiverades
övergången till rotation av att man använde svänghjul för att driva motorns
ickedrivande takter. Men med dagens magnetmaterial och halvledarteknik kan
man åstadkomma detta med elektrisk drivning vilket skulle innebära att man
slipper hela vevpartiet, alla problem med propelleraxelgenomföringar och alla
förluster i form av vattenrotation. Man kan i stället låta den fram- och
återgående kolven verka direkt mot vattnet.
De första och viktigaste frågorna som man alltid måste ställa sig vid
teknisk utveckling är alltså "Vad är önskat resultat?" och "Finns det
något enklare sätt att uppnå detta?".
Det finns en vandringssägen om hur man inom NASA drev ett projekt med
syfte att ta fram en lättare rakapparat som astronauterna skulle kunna
ha vid längre resor. Projektet pågick tills en av teknikerna gick ner
till butiken på hörnet och köpte en rakhyvel.
Hastighet
=========
Jag träffade en gång i tiden en pedagog som sa:
"När eleverna kommer till skolan vet de mycket väl vad hastighet är. Så
inför vi begreppet hastighet som kvoten mellan väg och tid och efter det
begriper de ingenting."
För att krångla till det ytterligare skulle jag vilja påstå att hastighet
är ett mått på hur stor andel av totala antalet händelser i universum som
flyttar en av de punkter som jag för tillfället är intresserad av i en viss
riktning.
Och så gäller det att reda ut det på ett begripligt sätt.
Betrakta en bil som kör på en väg. Lägg in ett koordinatsystem på sådant
sätt att lägeskoordinaterna för punkter i vägen förblir i stort sett
konstanta. När bilen fått upp farten kommer lägeskoordinaterna för en
partikel i bilen att ändras. Och denna partikel är kopplad till övriga
partiklar i bilen på sådant sätt att sannolikheten är stor att även
dessas koordinater skall ändras på liknande sätt.
Och varje gång en händelse inträffar i universum ökar tiden ett tids-
inkrement.
Om vi läser av lägeskoordinaterna för en partikel i bilen,väntar tills
tiden ökat med ett visst antal händelser (t ex en sekund) och därefter
på nytt läser av lägeskoordinaterna för partikeln får vi alltså veta hur
mycket partikelns läge ändrats under det att ett visst antal händelser
inträffat i universum. Men minsta detekterbara lägesförändring är en
händelse och att vi får veta hur mycket läget ändrats betyder alltså
att vi får veta hur många detekterbara lägesförändringar i rörelse-
riktningen partikeln gjort d v s hur många av alla händelser som inträffat
i universum som avsåg förflyttning av vår partikel i rörelseriktningen.
Om vi dividerar detta antal händelser med totala antalet händelser d v s
om vi dividerar lägesändringen för vår partikel med den tid som läges-
förändringen tagit får vi det som vi brukar kalla hastighet.
Vad jag gör när jag trampar ner gaspedalen i bilen är alltså att jag
försöker få en större andel av alla de händelser som inträffar i
universum att handla om att bilens läge på vägen ändras.
Om bilen flyttar sig sträckan s på tiden τ blir hastigheten v där
v = s/τ
Men om jag trampar på gasen ökar hastigheten. Om jag beräknar hastigheten
som s/τ får jag medelvärdet av hastigheten under tiden τ. Ibland är det vad
jag vill ha men ibland är jag mer intresserad av att veta hur stor
hastighet jag uppnått vid slutet av tiden τ (eller av något annat).
Hur beräknar man hastighet när den inte är konstant under mättiden?
Låt oss börja med att se på det enkla fallet att hastigheten är
proportionell mot tiden.Vi kan då skriva
v = a τ
där proportionalitetskonstanten a kallas för accelerationen.
Hur långt kommer ett föremål som från hastigheten noll accelererar med
accelerationen a under tiden τ?
Efter tiden τ är hastigheten v = a τ men medelhastigheten under tiden τ
blir hälften så stor d v s
v = a τ/2
medel
och sträckan s som föremålet tillryggalägger blir
s = v τ = a τ2 /2
medel
Men varför är det intressant att se på fallet med konstant acceleration?
Är det bara för att det är lätt att räkna på eller är det för att sådant
förekommer i verkligheten?
Om man påverkar ett föremål med konstant kraft får man faktiskt (bortsett
från luftmotstånd,friktion o dyl) konstant acceleration. Kraften F på ett
föremål med massan m ger accelerationen a enligt
F = m a
Och ett vanligt fall där man har konstant kraft är vid fallrörelser. Jordens
dragningskraft påverkar ett föremål vid jordytan med en kraft som är
praktiskt taget proportionell mot föremålets massa. När vi släpper ett
föremål och låter det falla fritt blir alltså accelerationen alltid densamma.
Vi får för fritt fall
a = 9,81 m/s2
För denna acceleration används ofta symbolen g.
Parametertid och koordinattid
=============================
Vi tänker oss en observatör som bara kan tänka i två dimensioner. Han ser
alltså världen projicerad på en yta på samma sätt som vi ser den med ett
öga eller när vi avbildar den med en kamera.
Om någon partikel ändrar höjd över denna yta förändras världen men det är
inte säkert att det märks i hans projektion. Indirekt kan han upptäcka
förändringen t ex genom att han flyttar sig så att partikelprojektionen
ändras. Han kan alltså ana sig till att hans bild är ofullständig och att
han bör ange denna typ av förändring genom att lägga till en tredje
koordinataxel.
På liknande sätt kan vi ana oss till att vi bör lägga till en tidsaxel
till vårt treaxliga rumssystem.
Om vi befinner oss i ett slutet rum,som vi kan kalla vårt observationsrum,
kan vi göra tankeexperimentet att vi bestämmer koordinaterna för alla
partiklar i rummet. Om vi så gör om bestämningen och finner att samtliga
koordinater är oförändrade är då allt oförändrat?
Nej det kan vi inte påstå för det kan ju ha inträffat händelser som förändrat
rummet i sin helhet i förhållande till världen i övrigt. För att ange det
behöver vi någon koordinataxel där vi kan avsätta observationsrummets läge
i förhållande till världen i övrigt. Vi kan kalla denna koordinat för
koordinattid.
Vi får då två tidsbegrepp som vi kan kalla
Parametertid
Koordinattid
Parametertid anger antalet händelser i universum oavsett var de inträffat.
Så snart någon partikel i universum ändrar läge så mycket att det är
detekterbart går alltså parametertiden ett tidsinkrement.
Koordinattiden går ett tidsinkrement varje gång en detekterbar händelse
inträffar utanför observationsrummet. En händelse som inträffar i
observationsrummet innebär att någon eller några rumskoordinater ändras
i observationsrummet. En händelse som inträffar utanför observationsrummet
innebär att koordinattiden ökar.
Antag att vi betraktar uppskjutning av en bemannad raket. Vi kan då lägga
x-axeln i raketens färdriktnig och strunta i y- och z-axlarna. Vi kan då
beskriva vad som händer i ett tvåaxligt koordinatsystem med en rumsaxel
(x-axeln) och en tidsaxel (koordinattid).
För oss är raketen en del av observationsrummet som ändrar läge i förhållande
till resten av observationsrummet. För besättningen ombord på raketen däremot
är raketens kontrollrum observationsrummet där,i stort sett allt står stilla.
Vi har lagt vår x-axel och vår axel för koordinattid så att huvuddelen av
vår omgivning har konstant x-koordinat medan raketens x-koordinat ökar.
Besättningen på raketen däremot lägger sin x-axel och sin axel för
koordinattid så att det mesta i raketen har konstant x-koordinat.
När raketen startar accelererar den men låt oss göra tankeexperinmentet att
den slår av motorn efter en stund och går med konstant hastighet. Dess bana
i vårt tvåaxliga koordinatsystem blir då en rät linje. Och besättningen på
raketen lägger sin axel för koordinattid längs denna räta linje. Raketens
hastighet innebär alltså att besättningens koordinatsystem vrids vinkeln
α i förhållande till vårt koordinatsystem. Och om vi mäter längd och
tid i samma enhet (t ex både längd och tid i meter eller både längd och tid
i sekunder) blir raketens hastighet sin α om vi använder parametertid
eller tan α om vi använder koordinattid.
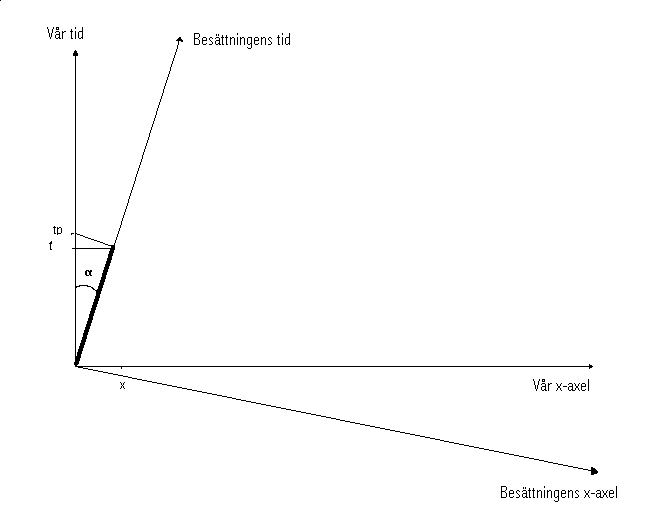 Fig 2
Eftersom raketen går sträckan x på vår parametertid τ eller på vår
koordinattid t säger vi att raketens hastighet är
x/τ = sin α
eller
x/t = tan α
Om hastigheten ökar så att raketen når ljushastigheten blir α 90 grader
och vår x-axel blir besättningens tidsaxel.
Att vi vanligen inte skiljer mellan parametertid och koordinattid beror på
att vi vanligen hanterar hastigheter som är så små i förhållande till
ljushastigheten att skillnaden mellan parametertid och koordinattid blir
liten.
Rörelseenergi
=============
Parametertid (τ) är alltså totala antalet händelser i universum,
koordinattid (t) är antalet händelser utanför observationsrummet och energi
(E)är den andel av totala antalet förutsägbara händelser som inträffar inom
observationsrummet.Om alla händelser inom observationsrummet kan anses vara
förutsägbara är
E = (τ - t)/τ
Vad blir då rörelseenergin för ett föremål, t ex en raket, som rör sig med
hastigheten v?
Enligt ovan gäller att
v = sin α
och om α är liten kan vi sätta
v = α
Av fig 2 framgår att
t = τ cos α = τ cos v
För små värden på v gäller att
cos v = 1 - v2 /2
vilket ger
(τ - t)/τ = v2 /2
Detta gäller för varje partikel i föremålet på en massenhet.Föremålets massa
m är antalet sådana partiklar och för hela föremålet får vi då rörelseenergin
E = m v2 /2
Intuition och konst
===================
När man kring mitten av det gångna årtusendet började verbalisera kunskap om
hur världen fungerade fick man nya möjligheter att utnyttja orsakskedjor och
förutsäga resultat av åtgärder. Sådan verbaliserad kunskap samlades och
systematiserades till det som brukar kallas vetenskap.
Men vetenskap omfattar inte allt.
Man säger att om fan skulle vilja luftkonditionera helvetet skulle han vända
sig till japanerna. De skulle göra en perfekt luftkonditionering utan att
ändra karaktären av helvete.
Läkarna talar om "Vetenskap och beprövad erfarenhet". Tekniska högskolor
lär ut "Konst och vetenskap". Man talar om "Ingenjörskonst".
Uppenbarligen inser man att det finns något som går utöver det som dagens
vetenskap omfattar.
I min ungdom byggde jag en gång en radio.Killen som stod vid arbetsbänken
intill frågade: "Vad ska det bli?". Jag svarade: "En radio". "Jaha! Men
varför är den så djävla ful?". Då slog det mig plötsligt att en radio var
något utöver beräkning av spolar, kondensatorer och motstånd. Det handlade
om att åstadkomma en produkt som skulle svara mot mänskliga önskemål. Och
en stor del av dessa önskemål låg utanför vetenskap och kunde enbart nås
via intuition. En intuition som krävde en speciell begåvning.
Under Kalle Ankas storhetstid tecknades Kalle av en tecknare som hette
Carl Barks. Att det blev en succe beror på att han hade denna begåvning att
"få till det". Med några få penndrag kunde han förmedla ett helt känsloliv
via ankbilder som inte ens hade mänskliga drag. Det finns t ex en bild i
Kalle Anka på Grönland där Kalle lurat iväg Alexander till Grönland och
inser att han har gått för långt. Han ser för sig en isbjörn som belåtet
klappar en fet mage med Alexanders damasker liggande framför sig på isen.
Och bilden av Kalle förmedlar hela den känslostorm som rasar inom honom.
Dagens tecknare har order att,så långt möjligt,efterlikna bilderna från
denna storhetstid.Vid första påseende är det hart när omöjligt att skilja
dem från en gammal klassiker. Men de förmedlar inga känslor!! De är
ritade för att efterlikna gamla, säljande bilder. Inte för att förmedla
upplevelser.
Och det samma gäller vår teknik att åstadkomma produkter. Det gäller inte
bara att få dem att fungera med hjälp av vetenskap.Det gäller att komma
längre än till att göra dem på rätt sätt. Det gäller att bli så säker på
hur man gör rätt att man vågar göra fel så att det blir bättre än rätt.
När vi har kommit dithän att alla kan få sina basala fysiologiska behov
uppfyllda måste vi gå vidare och ställa krav på,och tillåta, experiment
med nya ideer. Vi måste släppa fram något annat än massproduktion a la
dagens Kalle Anka. Något annat än efterapningar som är "tillräckligt bra".
Den verbaliserade vetenskapen kan beskriva en plog och namnge alla delar.
Den kan sätta upp kriterier för när man bör och när man inte bör plöja.
Den kan tala om vilken ände på plogen som skall vara framåt och vilka
delar som skall gå ner i jorden. Men den kan inte lära någon att plöja.
För att man skall "få till det", för att man skall få god skörd, för att
man skall vinna plöjningstävlan krävs något mer. Något som man bara kan
få genom kontakt med verkligheten.
De informationsmängder som skall bearbetas för att vi skall kunna räkna
oss fram till önskat resultat är ofta så enorma att vi måste utnyttja
genvägar som livet skapat under miljontals år av utveckling. Genvägar
som vi inte kan verbalisera, bara överföra via den gamla metoden från
mästare till lärling.
Kvantfysiken visade att vi inte kan härleda orsaker i all oändlighet,att
möjligheten att förutsäga vad som kommer att hända är begränsad.På liknande
sätt kan man säkerligen visa att möjligheterna att verbalisera all kunskap
är begränsad.Att vi behöver alla genvägar vi kan finna.Att vi borde vara
rädda om den overbaliserade kunskap som gångna generationer skapat.Att
dagens metoder att slå ut hantverk och konst med hjälp av det ekonomiska
systemet är mer än lovligt korkade.
Stabilitet
==========
Man upptäckte att det var möjligt att åstadkomma drivande maskiner som
omvandlade naturligt förekommande förändringar till användbar rörelse,
t ex till en roterande axel. Och man upptäckte att det var möjligt att
åstadkomma drivna maskiner som omvandlade en enkel rörelse, t ex en
vridning hos en roterande axel, till att utföra komplicerade sysslor.
Nu gällde det att "få till det"!
Ett problem som överraskade 1800-talets tekniker var att man fick
instabila system.
För att en maskin skall kunna utföra sin uppgift på rätt sätt krävs ofta
att någon eller något övervakar resultatet och styr maskinen efter vad
den åstadkommer. Detta kallas återföring.
Till en början använde man oftast människor som led i återföringslänkar.
För att styra en bil låter man en förare observera vägen och, via ratt,
gaspedal och broms, återföra styrsignaler till bilen. På ett fartyg lät
man styrmannen på bryggan observera och via maskintelegraf och maskinist
återföra styrsignaler till maskinen.
Men det visade sig snart att den långa återföringskedjan på ett fartyg
innbar problem. På den tid det tog för signalen att gå från styrman via
telegraf, maskinist och maskinpådrag kunde mycket oförutsett hända. Och
när bilarnas hastighet ökade blev förarens reaktionstid ett allt större
problem. I värsta fall kunde åtgärder som vidtogs för att avhjälpa ett
fel bli sådana som förvärrade det innan de nådde fram till verkställighet.
Stora tunga system blir ofta långsamma. Vi tycks ha en egendomlig vanföre-
ställning att en sådan långsamhet skulle göra det lättare att uppnå
stabilitet. Man försöker skapa stabila enheter genom att slå samman företag
till gigantiska koncerner och man lägger samman länder till handelsblock för
att få stora stabila enheter. Men man glömmer att den långsamhet som man
uppfattar som stabilitet beror på att systemen blir allt svårare att styra.
Att det tar längre tid för en supertanker än för en eka med aktersnurra att
ändra kurs betyder inte att det är lättare att styra en supertanker.
Och egentligen är det inte stabila system vi eftersträvar. Vi vill ha
system som skenar mot en bättre värld. Det är bara när det går åt fel håll
som vi har nytta av att veta hur vi uppnår stabilitet.
Första gången man kör en bil på isbana brukar man parera en sladd på sådant
sätt att den förvärras. Det är först efter en hel del träning som man lär
sig att häva en sladd. Vid första försöket blir styrningen ett instabilt
system som med växande rattutslag går mot att bilen stannar mot skyddsvallar
eller dylikt.
På vissa bandspelare används ett huvud för inspelning och ett för avspelning.
Om avspelningshuvudet sitter efter inspelningshuvudet kan man ansluta en
mikrofon och spela in sig själv samtidigt som man, med viss fördröjning,
lyssnar på resultatet. Men det brukar medföra att man förlorar talförmågan.
Korta och enkla ord brukar gå ganska bra men för mer komplicerade ord
lyssnar vi tydligen på oss själva så att vi kan rätta vårt uttal efter vad
vi hör. Men om vi inte hör vad vi säger när vi säger det utan vad vi sade
för en liten stund sedan fungerar inte detta. Metoden kan användas för att
testa om någon som påstår sig vara döv talar sanning men den är inte helt
tillförlitlig för även här kan vi, genom träning, lära oss att åstadkomma
ett godtagbart resultat även under dessa förhållanden.
När vi själva ingår i en överföringsloop från önskemål till verklighets-
förändring kan vi alltså ibland ändra vårt sätt att reagera så att vi
undviker oönskade resultat. Men om vi vill att ett tekniskt system
skall fungera på avsett sätt måste vi från början se till att vi inte
bygger in några instabiliteter i systemet. Servostyrningen i en bil skall
hjälpa till att vrida hjulen så mycket som vi vrider ratten, varken mer
eller mindre. Servobromsar skall ge en bromskraft som motsvarar
nedtryckningen av bromspedalen, varken mer eller mindre. O s v.
För att kunna studera stabilitetsproblem närmare måste man börja med att
välja någon typ av system som lätt kunde bli instabilt och som kunde anses
representativt för många olika fall av instabilitet. Ett sådant modellsystem
fann man i den återkopplade förstärkaren.
Fig 2
Eftersom raketen går sträckan x på vår parametertid τ eller på vår
koordinattid t säger vi att raketens hastighet är
x/τ = sin α
eller
x/t = tan α
Om hastigheten ökar så att raketen når ljushastigheten blir α 90 grader
och vår x-axel blir besättningens tidsaxel.
Att vi vanligen inte skiljer mellan parametertid och koordinattid beror på
att vi vanligen hanterar hastigheter som är så små i förhållande till
ljushastigheten att skillnaden mellan parametertid och koordinattid blir
liten.
Rörelseenergi
=============
Parametertid (τ) är alltså totala antalet händelser i universum,
koordinattid (t) är antalet händelser utanför observationsrummet och energi
(E)är den andel av totala antalet förutsägbara händelser som inträffar inom
observationsrummet.Om alla händelser inom observationsrummet kan anses vara
förutsägbara är
E = (τ - t)/τ
Vad blir då rörelseenergin för ett föremål, t ex en raket, som rör sig med
hastigheten v?
Enligt ovan gäller att
v = sin α
och om α är liten kan vi sätta
v = α
Av fig 2 framgår att
t = τ cos α = τ cos v
För små värden på v gäller att
cos v = 1 - v2 /2
vilket ger
(τ - t)/τ = v2 /2
Detta gäller för varje partikel i föremålet på en massenhet.Föremålets massa
m är antalet sådana partiklar och för hela föremålet får vi då rörelseenergin
E = m v2 /2
Intuition och konst
===================
När man kring mitten av det gångna årtusendet började verbalisera kunskap om
hur världen fungerade fick man nya möjligheter att utnyttja orsakskedjor och
förutsäga resultat av åtgärder. Sådan verbaliserad kunskap samlades och
systematiserades till det som brukar kallas vetenskap.
Men vetenskap omfattar inte allt.
Man säger att om fan skulle vilja luftkonditionera helvetet skulle han vända
sig till japanerna. De skulle göra en perfekt luftkonditionering utan att
ändra karaktären av helvete.
Läkarna talar om "Vetenskap och beprövad erfarenhet". Tekniska högskolor
lär ut "Konst och vetenskap". Man talar om "Ingenjörskonst".
Uppenbarligen inser man att det finns något som går utöver det som dagens
vetenskap omfattar.
I min ungdom byggde jag en gång en radio.Killen som stod vid arbetsbänken
intill frågade: "Vad ska det bli?". Jag svarade: "En radio". "Jaha! Men
varför är den så djävla ful?". Då slog det mig plötsligt att en radio var
något utöver beräkning av spolar, kondensatorer och motstånd. Det handlade
om att åstadkomma en produkt som skulle svara mot mänskliga önskemål. Och
en stor del av dessa önskemål låg utanför vetenskap och kunde enbart nås
via intuition. En intuition som krävde en speciell begåvning.
Under Kalle Ankas storhetstid tecknades Kalle av en tecknare som hette
Carl Barks. Att det blev en succe beror på att han hade denna begåvning att
"få till det". Med några få penndrag kunde han förmedla ett helt känsloliv
via ankbilder som inte ens hade mänskliga drag. Det finns t ex en bild i
Kalle Anka på Grönland där Kalle lurat iväg Alexander till Grönland och
inser att han har gått för långt. Han ser för sig en isbjörn som belåtet
klappar en fet mage med Alexanders damasker liggande framför sig på isen.
Och bilden av Kalle förmedlar hela den känslostorm som rasar inom honom.
Dagens tecknare har order att,så långt möjligt,efterlikna bilderna från
denna storhetstid.Vid första påseende är det hart när omöjligt att skilja
dem från en gammal klassiker. Men de förmedlar inga känslor!! De är
ritade för att efterlikna gamla, säljande bilder. Inte för att förmedla
upplevelser.
Och det samma gäller vår teknik att åstadkomma produkter. Det gäller inte
bara att få dem att fungera med hjälp av vetenskap.Det gäller att komma
längre än till att göra dem på rätt sätt. Det gäller att bli så säker på
hur man gör rätt att man vågar göra fel så att det blir bättre än rätt.
När vi har kommit dithän att alla kan få sina basala fysiologiska behov
uppfyllda måste vi gå vidare och ställa krav på,och tillåta, experiment
med nya ideer. Vi måste släppa fram något annat än massproduktion a la
dagens Kalle Anka. Något annat än efterapningar som är "tillräckligt bra".
Den verbaliserade vetenskapen kan beskriva en plog och namnge alla delar.
Den kan sätta upp kriterier för när man bör och när man inte bör plöja.
Den kan tala om vilken ände på plogen som skall vara framåt och vilka
delar som skall gå ner i jorden. Men den kan inte lära någon att plöja.
För att man skall "få till det", för att man skall få god skörd, för att
man skall vinna plöjningstävlan krävs något mer. Något som man bara kan
få genom kontakt med verkligheten.
De informationsmängder som skall bearbetas för att vi skall kunna räkna
oss fram till önskat resultat är ofta så enorma att vi måste utnyttja
genvägar som livet skapat under miljontals år av utveckling. Genvägar
som vi inte kan verbalisera, bara överföra via den gamla metoden från
mästare till lärling.
Kvantfysiken visade att vi inte kan härleda orsaker i all oändlighet,att
möjligheten att förutsäga vad som kommer att hända är begränsad.På liknande
sätt kan man säkerligen visa att möjligheterna att verbalisera all kunskap
är begränsad.Att vi behöver alla genvägar vi kan finna.Att vi borde vara
rädda om den overbaliserade kunskap som gångna generationer skapat.Att
dagens metoder att slå ut hantverk och konst med hjälp av det ekonomiska
systemet är mer än lovligt korkade.
Stabilitet
==========
Man upptäckte att det var möjligt att åstadkomma drivande maskiner som
omvandlade naturligt förekommande förändringar till användbar rörelse,
t ex till en roterande axel. Och man upptäckte att det var möjligt att
åstadkomma drivna maskiner som omvandlade en enkel rörelse, t ex en
vridning hos en roterande axel, till att utföra komplicerade sysslor.
Nu gällde det att "få till det"!
Ett problem som överraskade 1800-talets tekniker var att man fick
instabila system.
För att en maskin skall kunna utföra sin uppgift på rätt sätt krävs ofta
att någon eller något övervakar resultatet och styr maskinen efter vad
den åstadkommer. Detta kallas återföring.
Till en början använde man oftast människor som led i återföringslänkar.
För att styra en bil låter man en förare observera vägen och, via ratt,
gaspedal och broms, återföra styrsignaler till bilen. På ett fartyg lät
man styrmannen på bryggan observera och via maskintelegraf och maskinist
återföra styrsignaler till maskinen.
Men det visade sig snart att den långa återföringskedjan på ett fartyg
innbar problem. På den tid det tog för signalen att gå från styrman via
telegraf, maskinist och maskinpådrag kunde mycket oförutsett hända. Och
när bilarnas hastighet ökade blev förarens reaktionstid ett allt större
problem. I värsta fall kunde åtgärder som vidtogs för att avhjälpa ett
fel bli sådana som förvärrade det innan de nådde fram till verkställighet.
Stora tunga system blir ofta långsamma. Vi tycks ha en egendomlig vanföre-
ställning att en sådan långsamhet skulle göra det lättare att uppnå
stabilitet. Man försöker skapa stabila enheter genom att slå samman företag
till gigantiska koncerner och man lägger samman länder till handelsblock för
att få stora stabila enheter. Men man glömmer att den långsamhet som man
uppfattar som stabilitet beror på att systemen blir allt svårare att styra.
Att det tar längre tid för en supertanker än för en eka med aktersnurra att
ändra kurs betyder inte att det är lättare att styra en supertanker.
Och egentligen är det inte stabila system vi eftersträvar. Vi vill ha
system som skenar mot en bättre värld. Det är bara när det går åt fel håll
som vi har nytta av att veta hur vi uppnår stabilitet.
Första gången man kör en bil på isbana brukar man parera en sladd på sådant
sätt att den förvärras. Det är först efter en hel del träning som man lär
sig att häva en sladd. Vid första försöket blir styrningen ett instabilt
system som med växande rattutslag går mot att bilen stannar mot skyddsvallar
eller dylikt.
På vissa bandspelare används ett huvud för inspelning och ett för avspelning.
Om avspelningshuvudet sitter efter inspelningshuvudet kan man ansluta en
mikrofon och spela in sig själv samtidigt som man, med viss fördröjning,
lyssnar på resultatet. Men det brukar medföra att man förlorar talförmågan.
Korta och enkla ord brukar gå ganska bra men för mer komplicerade ord
lyssnar vi tydligen på oss själva så att vi kan rätta vårt uttal efter vad
vi hör. Men om vi inte hör vad vi säger när vi säger det utan vad vi sade
för en liten stund sedan fungerar inte detta. Metoden kan användas för att
testa om någon som påstår sig vara döv talar sanning men den är inte helt
tillförlitlig för även här kan vi, genom träning, lära oss att åstadkomma
ett godtagbart resultat även under dessa förhållanden.
När vi själva ingår i en överföringsloop från önskemål till verklighets-
förändring kan vi alltså ibland ändra vårt sätt att reagera så att vi
undviker oönskade resultat. Men om vi vill att ett tekniskt system
skall fungera på avsett sätt måste vi från början se till att vi inte
bygger in några instabiliteter i systemet. Servostyrningen i en bil skall
hjälpa till att vrida hjulen så mycket som vi vrider ratten, varken mer
eller mindre. Servobromsar skall ge en bromskraft som motsvarar
nedtryckningen av bromspedalen, varken mer eller mindre. O s v.
För att kunna studera stabilitetsproblem närmare måste man börja med att
välja någon typ av system som lätt kunde bli instabilt och som kunde anses
representativt för många olika fall av instabilitet. Ett sådant modellsystem
fann man i den återkopplade förstärkaren.
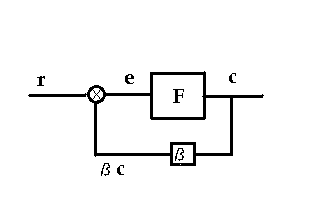 Fig 3
Man utgår från en förstärkare som förstärker insignalen e med råförstärkningen
F till utsignalen c. När man ökar förstärkningen växer c och därmed βc och
närmar sig r. Det medför att e minskar och går mot noll när F går mot
oändligheten. För höga värden på F gäller alltså att
r = β c
c = r/β
Om man t ex vill åstadkomma ett förstärkarsteg med förstärkningen 10 gånger gör
man en spänningsdelare som ger β = 0,1. Även om F varierar mellan t ex
10 000 och 1000 000 gånger kommer då c att vara praktiskt taget 10 r.
Men ovanstående resonemang förutsätter att signalen inte fördröjs innan den
jämförs med r. Om en sinusformad signal fördröjs med halva periodtiden byter
den tecken. Då blir inte felsignalen skillnaden mellan r och βc utan summan
av r och beloppet av βc. Ökande F medför då inte att e minskar. e kommer
i stället att öka Om β F > 1 kommer då c att gå mot oändligheten oavsett
vad r är. Förstärkaren ger alltså ifrån sig en signal som är så stor att
förstärkaren bottnar oberoende av vilken insignal den fått.
Anordningen blir alltså instabil om det finns en frekvens där signalen fördröjs
en halv period samtidigt som β F (den s k loopförstärkningen) är större än 1.
Vanligtvis blir födröjningen allt större del av periodtiden när frekvensen ökar,
d v s fasvridningen ökar med ökande frekvens.
Ökande frekvens brukar också medföra att förstärkningen minskar.
Om man konstruerar en förstärkare och en återföringsloop så att β F < 1 när
fasvridningen blir 180 grader får man alltså en stabil förstärkare.
Genom att ersätta tidsfunktionerna r , e , c , F och β med motsvarande
Laplacetransformer får vi en möjlighet att samtidigt hantera amplitud och
fördröjning. Metoden är teoretiskt elegant och i vissa sammanhang användbar
men den ställer ganska stora krav på att användaren behärskar övergången
mellan tidsfunktioner och Laplacetransformer.
Ett annat sätt att samtidigt hantera amplitud och fördröjning är att använda
komplexa tal. En signal kan delas upp i och beskrivas som en summa av
sinusformade signaler (Fourier-uppdelning). En beskrivning av hur en
förstärkare uppför sig för sinusformade signaler av olika frekvens ger
alltså en fullständig bild av hur förstärkaren uppför sig för godtyckliga
signaler. Man kan då använda komplexa tal där beloppet motsvarar
amplitud och argumentet motsvarar fasvridning. Man kan då i det
komplexa talplanet rita kurvor som visar hur förstärkningen blir vid
olika frekvenser. Om en sådan kurva omsluter punkten -1 + i0 är
förstärkaren instabil (Nyquist-kriteriet).
Ett annat sätt att formulera Nyquist-kriteriet är: Om förstärningen vid
någon frekvens ger fasvridningen 180 grader samtidigt som dess
belopp är större än 1 blir förstärkaren instabil.
Det går alltså att formulera villkor för stabilitet hos den återkopplade
förstärkaren och i många andra sammanhang kan man se att förhållandena
kan hanteras på samma sätt.
DEL 3
Hur fungerar världen?
=====================
Aristoteles (384 - 322 f Kr) gjorde en ganska omfattande sammanställning av
vad som då var känt.Han och hans efterföljare sa i princip:
Världen är vad den synes vara eller borde vara
Tunga föremål faller fortare än lätta.Stora hus är större än små och skall
alltså avbildas större.Solen och stjärnorna rör sig över himlen.Det finns
fyra aggregationstillstånd jord = fast fas , vatten = vätska , luft = gas ,
eld = plasma och kanske ett femte "de vises sten" = kollapsad stjärnmateria
och av dessa tillstånd är allt uppbyggt.
I stort sett stod sig denna uppfattning i ett och ett halvt årtusende.
Världen fungerade enligt av Gud givna lagar.Men Gud kunde bryta mot lagarna
och bistå enskilda människor.Och han var stor nog att bry sig om varje
människa.Det kunde löna sig att be om underverk,särskilt om man anlitade
prästerlig konsulthjälp.
Men tankebyggnaden började knaka i fogarna.Om man avbildade stora hus små
när de var långt borta blev bilderna mer lika verkligheten än när man
använde "korrekt" storlek.
Copernicus (1473 - 1543) visade att man fick en enklare bild av verkligheten
om man tänkte sig att jorden roterar kring sin axel och kring solen.
Galilei (1564 -1642) spädde på med att visa att man kunde se Jupiters månar
rotera kring planeten om man använde en kikare.Och han visade även att
påståendet att tunga föremål faller fortare än lätta bara gäller om de
lätta har större luftmotstånd i förhållande till sin vikt.
Påven, som såg hur fotfästet för hela världsuppfattningen höll på att gå
förlorat, försökte förgäves stoppa sådana ideer.
Newton (1642 -1727) visade att händelseförlopp kunde beräknas och förutses i
en utsträckning som man dittills inte kunnat tänka sig.Guds ingripanden
behövdes i långt mindre omfattning än vad man föreställt sig tidigare.En stor
del av förtröstan på Guds godhet kunde flyttas över på en förlitan på att
världen var förutsägbar.Gud hade skapat världen så att han mycket sällan
behövde ingripa. Världsuppfattningen fick ett nytt fotfäste.
För närobservationer använder vi känsel,hörsel,lukt,smak och syn men för fjärr-
observation är vi praktiskt taget helt hänvisade till synen.Kunskap om ljus
spelar därför en avgörande roll för vår världsuppfattning.Maxwell (1831 - 1879)
gav med den elektromagnetiska ljusteorin en mycket elegant beskrivning av ljus.
Men han väckte också en besvärlig fråga.
Maxwells ekvationer beskriver ljus som en vågrörelse mellan elektriskt och
magnetiskt fält.Men det finns ingen knytning av denna vågrörelse till ett
vågbärande medium. Vattenvågor bärs av vatten,ljudvågor bärs av luft och vi
kan definiera vågornas hastighet i förhållande till vattnet eller luften.
Och om vattnet eller luften strömmar påverkas även vågornas rörelse. Men
Maxwells ekvationer visade inte på något sådant för ljus!!
När Michelson (1852 - 1931) och Morley försökte mäta jordens hastighet
i förhållande till den ljusbärande världsetern blev resultatet noll.Liksom den
fasta jorden hade rubbats av Copernicus sviktade nu den fasta världsetern.
Einstein (1879 - 1955) hävdade att vi måste överge föreställningen att alla ser
samma värld.Om två observatörer rör sig i förhållande till varandra upplever de
att den andres klocka och meterstav påverkas av rörelsen.
Heisenberg (1901 - 1976) visade att vi inte samtidigt kan mäta tid och energi
med hur stor noggrannhet som helst.Och mätningarna påverkar vad vi mäter.Trots
att vi kommit på hur man kan bygga förstärkare som förstärker en signal till
vilken styrka som helst finns det gränser för hur noggrant man kan mäta.
Fotfästet i en av Gud given värld som är oberoende av alla observatörer sviktade.
Men om vi delar upp tidsbegreppet i koordinattid och parametertid där
koordinattid är en rumskoordinat likvärd de övriga tre och parametertiden är
en förändringsparameter då kanske vi åter kan se en eter,ett alluppfyllande
Brahma.Ett Brahma som strömmar med ljushastighet som en etervind. En etervind
som vi svävar i som ballonger eller moln som följer vinden. En vind som kan
blåsa åt olika håll i det tredimensionella rummet genom att etern är
kompressibel och/eller att etervinden i koordinattidsled kan variera. En värld
som är lika för alla betraktare men där den tredimensionella projektionen av
den fyrdimensionella världen kan variera för olika betraktare.
Vad är verklighet?
==================
Vi lever i en värld som förändras.Denna värld observerar vi med
sinnen som registrerar förändringar.
Om man sätter ett finger mot en bordsyta känner man när fingret
vidrör bordsytan.Men om man håller kvar fingret försvinner
känslan.Vårt känselsinne registrerar alltså inte kontakten med
bordsytan utan bara förändringen när fingret sätts mot bordet.
Om man håller ögonen orörliga under tillräckligt lång tid för-
svinner synintrycket.För att vi skall se något räcker det inte
med förändringarna när enskilda fotoner träffar näthinnan.Hela
mönstret i bilden måste förändras för att vi skall se något.
Vi ser inte världen sådan den är.Vi ser förändringar av världen.
Det vi upplever som verklighet är alltså inte verkligheten utan
förändringen av verkligheten.Vi ser inte verkligheten utan verk-
lighetens tidsderivata.
Bakom den verklighet vi upplever när våra sinnen registrerar
förändringar finns alltså en verklighet som förändras.
Ett föremål som ett hus kan förefalla vara en stabil oföränder-
lig företeelse men för att vi skall kunna veta att det finns
måste det förändra ljusstrålar som faller på det eller stoppa upp
vår handrörelse när vi tar på det.Våra sinnen registrerar alltså
enbart förändringar runt huset.Vi kan bara indirekt sluta oss
till att huset finns.
Våra sinnen informerar oss om förändringar i vår omvärld och vi
finner att många av dessa kan beskrivas genom att vi antar att
det finns en bakomliggande verklighet som orsakar dessa föränd-
ringar.Utifrån de förändringar vi registrerar kan vi dra vissa
slutsatser om denna verklighet men vi kan inte få veta allt om
den.
Om världen kan beskrivas av någon sorts funktion som har en tids-
derivata och om vi kan registrera tidsderivatan kan vi integrera
denna tidsderivata för att komma till ursprungsfunktionen.Men vi
vet att integration ger en obestämd integrationskonstant.Tids-
derivatan innehåller alltså inte all information om ursprungs-
funktionen.
Den värld vi upplever med våra sinnen är alltså förändringar av
en bakomliggande verklighet.Och för de flesta av oss gäller att
all vår strävan går ut på att styra dessa förändringar och
därigenom anpassa världen efter våra önskemål.
För att vi skall kunna uppfatta något måste världen innehålla
företeelser som avviker från omgivningen (kvanta) och dessa måste
bilda händelser genom att ändra läge i förhållande till varandra.
Vi kan inte se kvanta bara händelser.
För att observera något måste vi förändra det vi observerar. Det
är bara genom att se hur det förändras som vi kan dra slutsatser om
hur det ser ut. Vi kan inte komma fram till "das Ding an sich", till
verkligheten sådan den är. Vi kan bara föreställa oss en verklighet
som förändras på det sätt som vi observerar.
Ju noggrannare vi mäter ju mer förändrar vi det vi mäter. Om vi vill
veta allt om hur stenarna ligger i ett tegelhus måste vi plocka bort
alla stenar och förändra huset till en tegelstenshög. Men så brukar
vi inte göra. Vi nöjer oss med att se ytan på ytliga stenar och
kanske plocka bort ett par stycken. Så antar vi att övriga stenar
ligger på samma sätt, d v s att mönstret upprepas. Det mesta av vår
världsuppfattning bygger på denna föreställning om mönsterupprepning.
Vi föreställer oss en värld där mönster upprepas som tapetmönster. En
värld där förändringar kan inträffa och bilda händelser som vi kan
registrera med våra sinnen så att vi kan dra slutsatser om hur mönstren
ser ut.
Denna mönsterupprepning är ett av de största mysterierna. Vi vet inte
varför det är så och mycket lite om de regler som den följer.
Plancks konstant - Alltets konstant
===================================
Betrakta ett universum som innehåller h stycken urskiljbara kvanta. Varje
sådant kvanta är så litet att det inte går att dela. Det kan bara finnas
eller inte finnas. Vi kan kalla ett sådant kvanta för enhetskvanta eller
på engelska unit-quanta och beteckna det med UQ. Sorten för h blir alltså UQ
Den minsta händelse som kan inträffa i detta universum är minsta detekterbara
lägesförändring för ett enhetskvanta i förhållande till övriga kvanta. En
sådan händelse kan vi kalla för enhetshändelse eller på engelska unit-event
och beteckna med UE.
Alla händelser kan delas upp i enhetshändelser men en enhetshändelse kan inte
delas upp. Den 'inträffar' eller 'inträffar icke'. Något däremellan finns inte.
Totala antalet enhetshändelser som någonsin inträffat i vårt universum kallas
för absolut tid ( egentligen absolut parametertid). Tidpunkten för en viss
händelse är totala antalet enhetshändelser som inträffat före händelsen.
Tiden mellan händelse A och händelse B är tidpunkten för händelse B minus
tidpunkten för händelse A. Tid betecknas med τ och sorten för tid blir
alltså UE.
Antag att vi intresserar oss för en viss del av vårt universum, t ex av en
kula. Av alla kvanta i universumet avgränsar vi då några som utgör kulan. Vi
kan beteckna dessa kvanta med E. Med E menar vi alltså ett visst antal
enhetskvanta och sorten för E blir alltså UQ. Då gäller att E/h anger hur
stor del av universum som kulan utgör.
Om det så inträffar en enhetshändelse är sannolikheten E/h att denna
enhetshändelse består i att något av de kvanta som utgör kulan ändrar läge.
På tiden τ inträffar τ enhetshändelser och varje gång är sannolikheten
E/h att något av de kvanta som utgör kulan ändrar läge. I uttrycket
τ E
a = -----
h
är alltså a det antal gånger som ett enhetskvanta som ingår i E ändrar läge
under tiden τ. Om man minskar τ och/eller E så att a blir mindre än ett
övergår a till att ange sannolikheten att något kvanta inom E ändrar läge under
tiden τ.
τ E UE UQ
Sorten för a = ----- blir ----------- d v s UE.
h UQ
Om vi avgränsar en så liten mängd kvanta ΔE och observerar den under så kort
tid Δτ att Δτ ΔE = h/2 kommer endast en halv enhetshändelse att
beröra ΔE d v s sannolikheten att någon händelse inträffar som berör ΔE blir
0,5. Detta är gränsen för att vi skall kunna se att något händer med ΔE.
(Heisenbergs osäkerhetsrelation).
Låt oss se på ett litet universum med h = 1000 UQ där vi avgränsar en kula
med E = 10 UQ. Det är då bara var hundrade UQ som tillhör E. Det är alltså
bara var hundrade enhetshändelse som innebär att något kvanta i E har
flyttats. Efter en förändring av E går det alltså 100 UE innan det på nytt
är dags för en förändring av E. Vi säger att E:s periodtid är 100 UE.
Periodtid betecknas T och har sorten UE. För att bestämma periodtiden
sätter vi a = 1 i uttrycket τ = a h/E och får alltså T = h/E. Egentligen
är alltså T = 1 h/E där 1 har sorten UE så att även T får sorten UE.
Inverterade värdet av periodtiden kallas för frekvens.
Frekvens betecknas f och har sorten UE-1. Frekvensen för E är
f = E/h alltså egentligen f = E/(1 h) där ettan har sorten UE.
h är alltså antalet enhetskvanta i hela universum. Sorten för h är alltså UQ.
Men h är också det antal enhetshändelser som erfordras för att rubba samtliga
enhetskvanta i universum. Ser vi det så har h sorten UE. Och om en viss
enhetshändelse inträffar är h det antal enhetshändelser som troligen inträffar
innan den upprepas. Även om vi ser h på det viset blir sorten UE.
Även om alltså sorten för h inte är helt entydig är värdet entydigt för ett
visst universum. För alla i vårt universum har h samma värde. Men trots det
har vi ingen bra metod att fastställa detta värde. Vi vet inte exakt hur stort
vårt universum är och därmed vet vi inte heller det exakta värdet på h. Vi har
alltså inget bra värde på h varken i sorten UQ eller UE. Om vi vill kan vi
emellertid vända på resonemanget och säga att vi mycket väl vet värdet på h
men vi vet inte hur stort ett enhetskvanta är och därför kan vi inte uttrycka
h i sorten UQ.
Vi använder inte enheterna UQ ch UE för att ange kvantamängder och tider.
Detta beror dels på att det skulle bli svårhanterligt stora tal dels på att
vi inte exakt kan fastställa storleken på ett UQ och på en UE. Vi använder
i stället sorter som Joule och sekund som är ett stort antal UQ resp UE.
På en sekund går det ett visst antal (ks) enhetshändelser. På en
Joule går det ett visst antal (kJ) enhetskvanta. För att avgöra
vad som händer med värdet på h om vi övergår till att ange τ i sekunder
och E i Joule kan vi utgå från uttrycket τ E = a h. Om vi övergår till
sekunder och Joule får vi
τ ks E kJ = a h
a h
τ E = --- ---
ks kJ
Vi bibehåller sorten UE för a och får då
h i Js lika med (h i UQ)/(ks kJ)
Sorten för h är inte entydig eftersom ett enhetskvanta under vissa
omständigheter motsvaras av en enhetshändelse. h får då samma värde
oberoende av om vi använder sorten UQ eller UE. Men använder vi i
stället sekund och Joule måste omräkningsfaktorerna komma på rätt
plats och vi får då entydigt sorten Js för h.
h kallas för Plancks konstant.
Bortom tid och rum
==================
När vi som barn blir medvetna om vår omgivning börjar vi fråga "Vad
finns bortom?" , "Vad fanns före?" och "Vad kommer efter?".Och varje
gång vi får ett svar förskjuter vi gränserna för den värld vi upplever
som känd och ställer på nytt samma frågor.
Till slut brukar vi bli avspisade med att frågorna är meningslösa och
att ingen kan svara på dem.Men så är det faktiskt inte.Vi kan faktiskt
ibland hitta absoluta gränser.Det kanske mest iögonfallande exemplet är
absoluta nollpunkten för temperatur.
När man upptäckte att gaser ökade tryck och/eller volym när man värmde
dem fick man ett sätt att mäta temperatur.Vår instinkt att fråga "Vad
finns bortom?" ledde till att man började fundera kring frågan "Hur
kallt kan det bli?".Och svaret var faktiskt inte "Hur kallt som helst".
Om man kylde en gas vid konstant tryck minskade dess volym.Men till slut
kom man till volymen noll.Och eftersom vi inte kan tänka oss vad negativ
volym skulle kunna vara insåg man att det finns en absolut nollpunkt för
temperatur.
När vi tittar på en avlägsen stjärna tittar vi inte bara långt bort, vi
tittar även bakåt i tid.Vi ser inte stjärnan sådan den ser ut nu utan
sådan den såg ut när ljuset lämnade den. Om solen plötsligt slocknade
skulle vi inte märka något förrän det gått 8 minuter. Fram till dess
skulle ljus som var på väg mot oss när den slocknade fortsätta att komma
fram. Vi ser alltså inte solen sådan den är utan solen för 8 minuter
sedan.Och avlägsna stjärnor kan vi se för miljarder år sedan.
Liksom man en gång i tiden undrade hur kallt det kunde bli kan vi fråga oss
hur långt och hur långt tillbaka vi kan se. Och även här är faktiskt inte
svaret "Hur långt som helst".
Ljus kan uppfattas som en vågrörelse och färger som frekvensen hos denna
vågrörelse. Blått ljus har hög frekvens och rött ljus har lägre frekvens.
Vitt ljus är en blandning av olika färger d v s av olika frekvenser men
blandningen är inte jämn. Frekvenserna är koncentrerade till s k
spektrallinjer som motsvarar egenskaper hos de ämnen som avgivit ljuset.
Spiller man lite saltvatten i lågan på en gasspis lyser lågan med en gul
färg som motsvarar en kraftig spektrallinje hos det natrium som ingår i
saltet.
När vi tittar på ljus från fjärran stjärnor finner vi att färgen har
förskjutits mot rött. Och det är inte fråga om en omfördelning av
färgintensiteter för alla spektrallinjer har fått lägre frekvens. Det är
alltså så att ljusets frekvens blir lägre ju längre bort vi tittar.
Det innebär att om vi tittar tillräckligt långt bort blir ljusets frekvens
noll.
Och liksom vi inte kan tänka oss en negativ volym kan vi inte tänka oss en
negativ frekvens. Vi kan alltså inte ha större avstånd än att ljuset som når
oss från det avståndet får frekvensen noll. Och vi kan inte ha längre tid
tillbaka än gångtiden för ljus som når oss från detta avstånd.
Hur ser då världen ut när vi kommer till största möjliga avstånd? Vi "ser"
där en värld som avger ljus med frekvensen noll d v s totalt mörker. En
värld där vi inte kan urskilja någonting. Där vi inte kan skilja två punkter
från varandra och alltså inte tala om deras läge och avstånd. En värld där
vi inte kan urskilja punkter så att vi kan säga att en händelse har inträffat
genom att deras läge har förändrats. En värld utan avstånd och utan händelser
d v s en värld utan rum och tid.
Man brukar uppskatta det största möjliga avståndet till mellan 10 och 20
miljarder ljusår och motsvarande tid blir alltså mellan 10 och 20 miljarder
år.
Rum och tid är alltså ändliga begrepp som endast har mening lokalt i den
värld där vi råkar befinna oss. Utanför denna världs rum och tid råder en
jämn fördelning, d v s ett totalt mörker där allt överallt är lika. Vi
kommer ur ett totalt mörker, vi går mot ett totalt mörker och vi omges
av ett totalt mörker. Men den störning av detta perfekta tillstånd som
vi kallar världen är tillräckligt stor för att vi skall kunna ha en hel
del skoj på vägen.
Tid
===
En stillastående värld är ointressant.
Det finns en gammal film,jag tror den hette "A kind of stopwatch" om en man med
ett stoppur som har den egenskapen att när han startar det stannar allt i hela
världen utom han själv.Han använder det för att plundra en bank där han i lugn
och ro kan gå omkring bland stillastående kunder och tjänstemän.Men när han skall
trycka igång världen igen tappar han uret i golvet så att det går sönder och han
blir fast i en meningslös stillastående värld.
Lyckligtvis står vår värld inte stilla.Den är stadd i ständig förändring.
För att få ett mått på världens förändring kan vi dela in den och se den som
summan av en massa små händelser.
Den minsta händelse vi kan observera innebär att någon urskiljbar punkt
förändrar sitt läge i förhållande till övriga urskiljbara punkter med den
minsta detekterbara lägesförändringen.Vi kan kalla en sådan händelse för
en enhetshändelse.Så kan vi dela in världens förändring i enhetshändelser
(det blir ett stort och ohanterligt tal men det blir ett ändligt tal).
Enligt föregående avsnitt kan vi finna en gräns för hur långt tillbaka vi
kan gå och vi kan alltså finna en siffra som anger totala antalet
enhetshändelser sominträffat i vår värld.Siffran blir stor och vi har inte
mätmetoder som gör att vi kan bestämma den särskilt noggrant men vi kan
konstatera att denna siffra finns och vi kan kalla den för "absolut tid".
Vi kan uppskatta den absoluta tiden till att nu vara c:a 15 10120
enhetshändelser.
Det finns en mängd olika uppskattningar av Hubble-konstanten men låt oss
anta att universums ålder är 15 miljarder år och radien 15 miljarder ljusår.
Medeltätheten kan uppskattas till 4 10-26 kg/m3. Vilket innebär att
totala innehållet är 2 1053 kg eller 2 1070 J.Om vi dividerar med Plancks
konstant får vi motsvarande frekvens som alltså blir 3 10103 Hz.
Inverterar vi det värdet får vi periodtiden som vi kan använda som mått på
kortast möjliga tid d v s som mått på den tid som åtgår för en enhetshändelse.
Vi får alltså fram att det går 3 10103 enhetshändelser på en sekund och
att en enhetshändelse tar 3 10-104 s.Då 15 miljarder år är 5 1017 s
innebär det att den absoluta tiden nu är c:a 15 10120 enhetshändelser
Men även om vi inte kan bestämma den absoluta tiden särskilt noggrant och även om
den absoluta tiden blir ohanterligt stor kan vi,med stor noggrannhet,mäta tiden
mellan två händelser som inträffar inom vårt observationsområde.
Av alla händelser som inträffar i universum är de allra flesta helt slumpmässiga.
Det är bara en mycket liten del som vi kan påverka.Men enhetshändelser har en
tendens att bilda mönster och samordnas till större händelser som vi kan
observera.Eftersom sådana inträffar helt slumpmässigt kan vi utgå från att om
vi nöjer oss med att observera en viss typ av händelse inom ett litet område så
får vi ett mått på totala antalet händelser.Vi kan t ex bygga ett pendelur och
räkna med att varje gång händelsen att pendeln fullbordat ett slag har inträffat
har det gått en sekund d v s har det inträffat 3 10103 enhetshändelser i hela
universum.Att den andel av det totala antalet händelser som vi mäter på detta sätt
är konstant kan vi övertyga oss om genom att göra två likadana klockor och se
om de går likadant.Vi finner då att om vi kan isolera dem från störande
inverkan utifrån går de nästan exakt lika.
Rum
===
På liknande sätt som vi kan definiera en enhetshändelse kan vi definiera en
enhetslängd.En enhetslängd är helt enkelt den sträcka ljuset hinner gå under en
enhetshändelse.
Vårt universum blir då ett rum i form av ett klot med radien 15 10120 enhetslängder.
Detta klot kan vi dela in i enhetsceller med en enhetslängd som sidlängd.Detta
klot rymmer alltså c:a 1 10364 enhetsceller.
Om vi även vill räkna in alla enhetsceller som någonsin funnits får vi betrakta
tid som en fjärde dimension.Vi får då ett fyrdimensionellt halvklot med c:a
1 10485 enhetsceller.
En enhetscell ligger på gränsen till att vara observerbar.Det går alltså inte att
urskilja några detaljer i den.Vi kan bara skilja mellan om den innehåller något eller
om den är tom.Vi kan alltså fullständigt beskriva den med en etta eller en nolla.
Världen är alltså ett "datorminne" som rymmer 10364 bits och som totalt
har hanterat 10485 bits.
Med "avstånd" mellan A och B menar vi det antal enhetsceller vi måste passera för att
komma från A till B.
Vi kan alltså se på världen som en dator med ett enormt minne.Men en dator är
praktiskt taget oanvändbar om den inte har ett operativsystem som gör att innehållet
i minnet ändras enligt vissa regler.Och även världen har sitt "operativsystem".Hur
detta fungerar är vad fysik egentligen handlar om.
Orsak och verkan
================
För att bli användbar behöver en dator något operativsystem med någon form av BIOS
(Basic In/Out System).Ännu mer fundamentalt är att man redan i processorns hårdvara
brukar lägga in vissa begränsningar av hur minnet kan förändras.Man brukar t ex
dela in minnet i grupper om 8 , 16 eller 32 bits som hanteras samtidigt.
För att kunna använda datorn måste vi komma fram till en förenklad uppfattning av
den,en uppfattning som är användbar och som kan rymmas inom vår tankeförmåga.Vi
börjar då med att bortse från ettor och nollor för att i stället se grupper av
bits som vi kallar bytes.
På liknande sätt finner vi att världen har ett "BIOS" som grupperar enhetsceller.
Sammanhängande grupper av enhetsceller kallar vi partiklar och vi finner att det
finns förvånansvärt stabila sådana.Av någon anledning förblir mönstret av ettor
och nollor inom en partikel ofta konstant även om partikeln ändrar läge i
förhållande till andra partiklar.
Ett sätt att se detta bevarande av mönster är att jämföra med ballonger i
byig vind. Dessa flyttas av vindbyar så att de ändrar läge i förhållande till
varandra men om ballongerna ligger tätt kommer inte en vindby att ändra det
inbördes läget för närliggande ballonger.
Även i tidsled grupperar världens "BIOS" enhetshändelser till händelsekedjor som
bildar urskiljbara mönster.Om vi vet vad som har hänt kan vi,i vissa fall,förutse
vad som kommer att hända.Om vi vet att en partikel har förflyttat sig i ett område
med enbart nollor kan vi förutse att den kommer att fortsätta förflyttningen.
Vi kallar den förflyttning som redan skett för orsak och den som vi förutser för
verkan.
Vi har funnit ett antal orsak-verkan-samband som vi kan använda som ett sorts
högnivåspråk för programering av världen.Om vi önskar en viss verkan men finner
att den är svår att uppnå kan vi leta bland dessa samband för att se om vi i
stället kan finna en orsak som är lätt att åstadkomma och som ger önskad verkan.
Eller en orsak som har en verkan som kan vara orsak till den önskade verkan.Eller
en orsak till en orsak till en orsak till verkan.
Människor har naturligtvis alltid använt sig av orsakskedjor för att nå sina mål.
Men till en början skedde detta huvudsakligen intuitivt.Att orsaka en spräckning
av ett flintstycke så att man får en användbar flintkniv är en konst som våra
förfäder utvecklade och förfinade.Man lärde sig orsakskedjorna men man
verbaliserade dem inte.Lärlingen lärde sig huvudsakligen genom att se och höra
mästarens slag och genom att själv slå med slagsten på flinta.
Kring mitten av det gångna årtusendet började en målmetveten strävan att
verbalisera orsak-verkan-samband.Detta lyckades över förväntan och så sent som
under adertonhundratalets slut trodde man på fullt allvar att varje verkan
kunde knytas till orsaker som i sin tur kunde knytas till orsaker.
Kvantfysiken och speciellt Heisenbergs osäkerhetsrelation bröt med denna
föreställning genom att hävda att ett orsak-verkan-samband säger att en orsak
innebär en viss sannolikhet för en viss verkan.Denna sannolikhet kan vara nära
ett men den är alltid mindre än ett.
Om man släpper en sten är sannolikheten stor att den faller nedåt.Men det finns
en liten,beräkningsbar,sannolikhet att den faller uppåt.Denna sannolikhet är
naturligtvis så liten att vi,för praktiskt bruk,kan strunta i den.Men att den
finns är principiellt viktigt för det innebär att världen kan komma med
överraskningar.
Heisenbergs osäkerhetsrelation bygger på insikten att världen både har partikel-
karaktär och vågkaraktär samtidigt.Men en våg måste observeras under åtminstone
större delen av periodtiden innan man kan veta att det verkligen rör sig om en
våg.En ansamling fyllda enhetsceller,d v s en ansamling ettor,kan bilda en
partikel.Ju fler ettor den innehåller ju högre säger vi att dess energi är.
Och när vi använder vågbeskrivning blir dess frekvens energin dividerad med
Plancks konstant.Ju högre energi den har ju högre frekvens och därmed kortare
periodtid har den.
Något förenklat kan man säga att Heisenberg påpekade att man måste observera
en energimängd under halva dess periodtid innan man säkert vet om den finns.
Om man vill veta hur stor en energimängd är och när den har denna storlek måste
man göra en nogrann mätning under kort tid.Men ju noggrannare man vill veta
hur stor den är ju längre tid tar mätningen.Och ju mer exakt man vill veta
mättidpunkten ju sämre hinner man mäta energiinnehållet.
Heisenberg konstaterade att om man samtidigt försöker mäta två storheter A och B
som har egenskapen att deras produkt har sorten Js så blir minsta möjliga fel
ΔA ΔB = h/2
där h = Plancks konstant.
Energi
======
Enhetshändelser inträffar och bildar mönster i form av händelsekedjor.Sådana
händelsekedjor kallar vi händelser.Händelser inträffar hela tiden.Dessa
händelser är helt enkelt tiden.
Av alla händelser som inträffar är det en mycket liten del som vi kan
förutse och påverka.Men hur liten den delen än är är den viktig för oss.Så
viktig att vi behöver ett särskilt begrepp för den.Vi kallar förutsebara,
påverkbara händelser för energi.
Det förefaller som om vi inte kan tömma eller fylla en enstaka enhetscell.
Vi kan alltså inte göra om en etta till en nolla eller tvärtom.Däremot kan
ettor byta plats med nollor.Så vitt vi vet består alla händelser vi observerar
i att ettor och nollor byter plats.Världens BIOS tycks se till att minnet hela
tiden har lika många ettor.
Nollor är mycket vanligare än ettor i vår värld.Om vi påträffar en fylld
enhetscell,d v s en etta,kan vi alltså förutse att den kommer att bytas ut mot
en nolla.De ettor vi observerar är alltså förutsägbara förändringar d v s
förutsägbara och därmed påverkbara händelser,d v s energi.
Den tätaste materia vi känner är den som finns i kollapsade stjärnor.Om vi
antar att denna materia består av enbart ettor kan vi uppskatta andelen ettor
i vår del av världen.En uppskattning av denna täthet är 3 1010 kg/m3.
Medeltätheten i vår del av världen rör sig om 4 10-26 kg/m3.
Förhållandet mellan dessa tätheter utgör ett mått på andelen ettor i vår värld.
Det går alltså c:a 1036 nollor på varje etta.
Även i den tätaste materia vi känner här på jorden går det mer än en miljon
nollor på varje etta.
En enhetshändelse innebär alltså att en etta och en nolla byter plats.Eftersom
antalet ettor är så mycket mindre än antalet nollor är det antalet ettor som
anger hur ofta detta sker.Antalet ettor inom en viss volym anger alltså hur
många förutsebara händelser som kommer att inträffa i volymen d v s hur stor
energi som finns i volymen.
Om man kan avgränsa en viss volym så att den inte kan utbyta ettor mot nollor
eller tvärsom över volymgränsen blir antalet ettor d v s energin konstant inom
volymen.
Detta brukar kallas för termodynamikens första huvudsats och formuleras som att
energin hos ett slutet system är alltid konstant.
Men en enhetshändelse är mycket liten,så liten att vi inte känner något sätt att
utnyttja en enstaka enhetshändelse.Att försöka finna en enstaka etta för att
kunna utnyttja att vi kan förutse att den kommer att bytas ut mot en nolla är
som att försöka manipulera gener med grävskopa.Våra sinnen,instrument och verktyg
är trubbiga och vi behöver enhetshändelser som sker samordnat till användbara
händelser.Om vi avgränsar en viss volym så att den bildar ett slutet system
kan det hända att fördelningen av ettor inom systemet är ojämn.Vi kan t ex
ha många fler ettor i ett hörn än i resten av volymen.Vi kan då,inte bara förutse
att varje etta kommer att bytas mot en nolla,vi kan förutse att sådana byten
kommer att ske oftare i detta hörn än i resten av volymen.Och detta kan ske i
en skala som vi kan använda.En sned fördelning av ettor inom ett slutet
system kan vi alltså använda.Men det är användbart därför att vi kan förutse
att fördelningen kommer att utjämnas och när vi använder det utjämnas för-
delningen och blir oanvändbar.
Detta brukar kallas för termodynamikens andra huvudsats.Den formulerades i en
tid när man främst var intresserad av att omvandla värme till arbete och när man
fann att man måste ha en sned temperaturfördelning för att omvandla värme till
arbete.Den brukar därför formuleras:Entropin (värmelärans motsvarighet till
ellärans laddning eller mekanikens tyngd) hos ett slutet system kan inte
minska.
En konsekvens av andra huvudsatsen är att tiden bara går åt ett håll.I stället
för att säga "Entropin hos ett slutet system kan inte minska" skulle vi kunna
säga "Tiden kan inte minska".
När vi var små spelade min bror och jag ibland schack.Det hände att vi hamnade
i lägen där vi inte kunde komma på vad vi skulle göra härnäst.Jag kunde då
flytta tornet ett steg för att i nästa drag återgå till utgångsläget och han
kunde göra likadant.Så kunde vi "spela" hur länge som helst utan att ställningen
förändrades.Spelet gick bara framåt av irreversibla drag t ex flyttning av en
bonde,att någon slog en pjäs eller att någon gjorde ett drag som öppnade nya
möjligheter.
Om en etta byter plats med en nolla går tiden fram en enhet.Men om nästa
enhetshändelse är att ettan återgår till utgångsläget går tiden bakåt en
enhet.Ingen kan veta att något har hänt.Alla minnen består av enhetsceller
och för att någon skall kunna minnas en händelse måste den orsaka en
händelsekedja som ställer om något minne.
Liksom schackspelet går tiden bara framåt av händelser som är eller som på
grund av andra händelser blir irreversibla.
När man började studera möjligheter att omvandla värme till arbete fann man
att man vanligen utgick från värme med hög temperatur och liten entropi för
att sluta med en rest av värme vid omgivningstemperatur med högre entropi
än utgångsvärmet.Entropiökningen innebar att man inte kunde komma
tillbaka till utgångsläget. Man började därför betrakta entropi som ett mått
på irreversibilitet.Och begreppet används idag i vidgad betydelse så att
man t ex vid kemiska reaktioner talar om en entropiterm som anger
reaktionens grad av irreversibilitet även om det inte direkt är fråga om
en omvandling till värme.
Med denna vidgning av begreppet blir alltså entropiökning en synonym till
tidökning.Och andra huvudsatsen utsäger det vi alla av erfarenhet vet,
nämligen att tiden bara går åt ett håll.
Termodynamikens första och andra huvudsatser är viktiga regler som vi kan
använda när vi försöker utnyttjas världens BIOS.Men utöver dem finns det andra
hinder för utjämning mellan ettor och nollor.Möjligheten att avgränsa slutna
system innebär att det finns möjligheter att "låsa in" ettor i avgränsade
volymer där utjämning med omgivningen inte sker trots att den borde göra det
enligt första och andra huvudsatsen.Vi har t ex inte funnit något sätt
att få materia att restlöst omvandla sig till andra energiformer trots
att första och andra huvudsatsen säger att det borde vara möjligt.
Arbete
======
Antag att jag skall lyfta en säck mjöl.
Jag skall då genomföra den procedur som inom datatekniken kallas för shift.
Via världens BIOS anropar jag shift-proceduren för alla de bits som utgör
säcken.Detta anrop omfattar en lång och komplicerad händelsekedja men på
samma sätt som en dators operativsystem gömmer programelement för operatören
är denna kedja okänd för mig.Jag vet bara att jag anropar shift-proceduren
genom att ta tag i säcken och lyfta.
När alla de bits som utgör säcken skiftats mot ovanförliggande bits har säcken
lyfts en enhetslängd och det är bara att anropa shift-proceduren på nytt och
på nytt tills jag fått upp den tillräckligt.
Jag finner nu att det krävs en viss viljeansträngning för att jag,på detta
sätt,skall anropa shift-proceduren.Utförande av något som kräver viljeansträng-
ning kallar vi arbete.Här på jorden är det tydligen så att det krävs arbete
för att lyfta föremål.Att lyfta är en typ av förflyttning och jag finner att
även andra typer av föremålsförflyttning kan kräva arbete.Inom fysik gör man
den förenklingen att man enbart talar om sådant arbete som är knutet till
förflyttning av föremål.
Om jag provar att lyfta olika säckar till olika höjd finner jag att det krävs
mer arbete att lyfta en säck ju högre jag lyfter den och det krävs mer arbete
ju mer det är i den.Åker jag till månen finner jag också att det krävs mer
arbete att lyfta en viss säck till en viss höjd på jorden än på månen.
Shift-proceduren innebär ju en förutsägbar och avsiktlig förändring.Den är
alltså energi.Arbete i fysikalisk mening är alltså en form av energi.Men även
om det krävs lika mycket energi,d v s arbete,för att lyfta en lätt säck till
hög höjd som att lyfta en tung säck till låg höjd är dessa procedurer olika
och vi behöver metoder att beskriva dem som visar hur de skiljer sig från
varandra.
Vi gör då en uppdelning i
Antal ettor som skall skiftas
En faktor som anger hur svårt det är att skifta på den plats man är
Antal shift-procedurer som krävs
Vi säger att
W = mg h
där
W = det arbete,d v s den energi,som krävs för lyftet (Work)
m = säckens massa d v s antalet ettor som ingår i säcken
g = gravitationskonstanten som är olika på jorden och på månen
h = lyfthöjden,d v s antal erforderliga shift-procedurer
Produkten mg kallar vi säckens tyngd.
Vi delar alltså upp energin i två faktorer där den ena (tyngden) anger hur stor
mängd vi arbetar med.Vi kallar denna faktor för extensiv faktor eller mängdfaktor.
Den andra faktorn anger hur stor förändring varje del av mängden utsätts för.Vi
kallar den faktorn för intensiv faktor.
För min mjölsäck är alltså tyngden (mg) extensiv faktor och lyfthöjden (h)
intensiv faktor.
Kraft
=====
Vi säger att mjölsäckens tyngd är en kraft.För att åstadkomma denna anropar
jag shift-proceduren via världens BIOS.Men jag finner att jag behöver göra
likadana anrop i en rad andra fall.Om jag skall dra ett föremål över ett
strävt underlag,om jag skall sätta fart på en sten för att kasta den,om
jag skall dra en båt i vatten måste jag göra likadana proceduranrop.Vi
kallar alla sådana anrop för kraft oavsett om vi åstadkommer dem själva
eller om vi utnyttjar någon maskin för att göra dem.
Att anbringa en kraft på ett föremål är en uppmaning till föremålet att
förflytta sig.Om det förflyttar sig sker en förändring d v s energi omsätts.
Kraften gånger förflyttningslängden är den omsatta energin.
För att kunna räkna med krafter behöver vi något hanterligt mått på dem.
Vi använder oss då av den regel i världens BIOS som säger att om ingenting
bromsar rörelsen kommer en kraft som verkar på en massa att öka dess hastighet.
Vi kallar den kraft som varje sekund ökar hastigheten hos en massa på 1 kg med
1 m/s för 1 N (Newton).Vi har alltså att
1 N = 1 kg m/s2
Vi använder oss av krafter för att åstadkomma önskade förändringar där och när
vi vill ha dem.Men förändringar inträffar också hela tiden spontant.Om vi vill
åka med ett luftskepp från Stockholm till Göteborg startar vi en drivmotor som
ger en kraft som förflyttar skeppet mot Göteborg.Denna kraft gånger den väg vi
färdas är det arbete,d v s den energi,som vi måste tillföra.Men det är viktigt
att observera att denna energitillförsel inte är nödvändig för att vi skall
komma till Göteborg i och för sig.Den är nödvändig för att vi skall kunna
förutsäga när vi kommer till Göteborg.Om vi lät skeppet driva omkring i luft-
havet i oändlig tid skulle vi naturligtvis,förr eller senare,hamna över
Göteborg och då skulle vi alltså ha fullbordat resan.Men det är ett mycket
opraktiskt sätt att resa.Vi behöver åtminstone någon typ av kraft som gör att
vi kan förutsäga färdvägen lite bättre.
Brus
====
Värme är slumpmässiga molekylrörelser (eller strålningsvärme). I en gas far
molekylerna omkring samtidigt som de roterar. I ett fast ämne vibrerar
molekylerna kring sina jämviktslägen.
Om man, med allt större noggrannhet försöker bestämma läget hos ytan av ett
stycke fast materia kommer man så småningom till problemet att det inte går
att komma längre därför att de atomer som utgör ytan hela tiden rör sig.
Om man observerar en liten partikel som svävar i en vätska finner man att
den rör sig med knyckiga slumpmässiga rörelser (Browns rörelse) som beror
på kollisioner med vätskemolekyler.
Kollisioner kan även medföra att elektroner slås ut från sina lägen i
elektronskalen vilket ger en slumpmässigt varierande spänning, d v s ett
elektroniskt brus.
När man i teleteknikens barndom försökte signalera över allt större avstånd
genom att förstärka den mottagna signalen med allt högre förstärkning fann
man att man inte bara förstärkte signalen utan också ett brus. Och när
signalen drunknade i bruset kunde man inte komma längre genom att öka
förstärkningen.
Slumpmässiga, d v s oförutsägbara, händelser inträffar. Det är bara en liten
del av alla händelser som är förutsägbara genom att de har en känd orsak.
Även när det finns en känd orsak kan det finnas oförutsägbarhet om detaljer i
verkan. Värme är en orsak till molekylrörelse men hastighet och riktning för
en enskild molekyl är oförutsägbar.
Temperatur är ett mått på variansen på molekylhastigheten. Om variansen är
skiljd från noll kan vi förutsäga att en viss molekyl kommer att röra sig men
det säger ingenting om åt vilket håll och det ger bara en antydan om hur
fort den kommer att röra sig.
För en ideal gas gäller
m s2 = 3 k T
där
m molekylens massa i kg
s2 variansen på den slumpmässiga molekylhastigheten
k Boltzmanns konstant
T absoluta temperaturen i K
Styrkan hos en signal avtar med avståndet (i tid och/eller rum) från orsaken.
Bruset beror på temperaturen hos bakgrunden och temperaturen hos mottagaren.
Med ökande avstånd kommer således signalen så småningom att drunkna i bruset.
Våra förutsägelser blir alltså alltmer osäkra.
Vi kan t ex göra väderprognoser baserade på dagens kända orsaker till väder-
förändringar men bruset genererar hela tiden oförutsägbara orsaker till
förändringar och allteftersom tiden går kommer dessa allt mer att dominera
över dagens kända orsaker.
Allt vi gör är alltså förgängligt. Vilken verkan vi än åstadkommer kommer den
så småningom att drunkna i de slumpmässiga förändringar som bruset orsakar.
Den fyrdimensionella världen
============================
Med avståndet mellan punkterna A och B menar vi det minsta antal enhetsceller
man måste passera för att komma från A till B.På liknande sätt kan man
definiera tidsavståndet mellan händelserna a och b som det antal enhetshändelser
som inträffar mellan a och b.
Ett sätt att hantera avstånd mellan ett stort antal punkter är att lägga in dem
i ett treaxligt koordinatsystem.I stället för att ange alla möjliga avstånd kan
vi då ange alla punkters koordinater och ur dessa beräkna de avstånd vi vill
veta.
Det ligger nära till hands att lägga till en koordinataxel och använda den för
att ange tidskoordinat.Med avstånd i ett sådant fyraxligt koordinatsystem menar
vi då,inte bara antal enhetsceller mellan A och B utan också antal enhetshändelser
mellan att vi utgår från A och kommer fram till B.
Om vi använder ett sådant fyraxligt koordinatsystem kan vi ge tid två olika
betydelser.Vi kan dels tala om tid som en förändringsparameter.Vi kan kalla
detta för parametertid.Och vi kan tala om tid som en lägeskoordinat i vår
fyrdimensionella värld.
Så kan vi naturligtvis göra men normalt växer parametertiden och koordinattiden
likadant.Finns det då någon anledning att skilja på begreppen?Finns det något
i världens BIOS som går att beskriva genom att vi skiljer på begreppen?
Världens BIOS uppför sig faktiskt som om det fanns något som strömmade med viss
hastighet åt något håll i den fyrdimensionella rymden.Vi har inget bra namn på
detta något.Det har kallats världseter eller Brahma men låt oss för enkelhets
skull kalla det för eter.
Om allt står stilla i rummet strömmar etern i tidsriktning.Och hastigheten blir
c = t/τ
där
c = eterns strömningshastighet d v s ljushastigheten
t = koordinattid
τ = parametertid
Allt står då stilla i rummet och följer med en eter som strömmar i tidsled.
Om något rör sig i rummet kan vi uppfatta detta som att hastigheten där ändrar
riktning.Om något föremål flyttar sig sträckan s på parametertiden τ säger vi
att det rör sig med hastigheten v enligt
v = s/τ = c sin(α)
där
α = vridningsvinkeln för föremålets hastighetsvektor
Man kan uppfatta ljus som en ström av partiklar,fotoner,som rör sig med ljus-
hastighet i rummet.Fotonernas hastighetsvektor har alltså vridits 90 grader så
att de rör sig i rummet men står stilla i tiden.
Om man,likt Munchhausen,kunde hoppa ombord på en foton och titta bakåt skulle
man se startplatsen sådan den såg ut när man startade.Alla klockor på startplatsen
skulle då stå stilla.Man skulle inte röra sig i startplatsens tidsled.Men man
skulle röra sig med ljushastighet i någon annan riktning som man själv skulle
uppfatta som tidsriktningen och de som var kvar på startplatsen skulle kalla en
rumsriktning.
Gravitation
===========
Betrakta två partiklar A och B på avståndet ab.
I fig 1 anger den blå ytan alla punkter som ligger närmare A än vad B gör.Och
den gula ytan anger punkter som ligger längre ifrån A än vad B gör.Om nu B
rör sig helt slumpmässigt i förhållande till A finns det uppenbarligen många
fler punkter dit B kan gå för att öka avståndet till A än punkter dit B kan
gå för att minska avståndet.
Fig 3
Man utgår från en förstärkare som förstärker insignalen e med råförstärkningen
F till utsignalen c. När man ökar förstärkningen växer c och därmed βc och
närmar sig r. Det medför att e minskar och går mot noll när F går mot
oändligheten. För höga värden på F gäller alltså att
r = β c
c = r/β
Om man t ex vill åstadkomma ett förstärkarsteg med förstärkningen 10 gånger gör
man en spänningsdelare som ger β = 0,1. Även om F varierar mellan t ex
10 000 och 1000 000 gånger kommer då c att vara praktiskt taget 10 r.
Men ovanstående resonemang förutsätter att signalen inte fördröjs innan den
jämförs med r. Om en sinusformad signal fördröjs med halva periodtiden byter
den tecken. Då blir inte felsignalen skillnaden mellan r och βc utan summan
av r och beloppet av βc. Ökande F medför då inte att e minskar. e kommer
i stället att öka Om β F > 1 kommer då c att gå mot oändligheten oavsett
vad r är. Förstärkaren ger alltså ifrån sig en signal som är så stor att
förstärkaren bottnar oberoende av vilken insignal den fått.
Anordningen blir alltså instabil om det finns en frekvens där signalen fördröjs
en halv period samtidigt som β F (den s k loopförstärkningen) är större än 1.
Vanligtvis blir födröjningen allt större del av periodtiden när frekvensen ökar,
d v s fasvridningen ökar med ökande frekvens.
Ökande frekvens brukar också medföra att förstärkningen minskar.
Om man konstruerar en förstärkare och en återföringsloop så att β F < 1 när
fasvridningen blir 180 grader får man alltså en stabil förstärkare.
Genom att ersätta tidsfunktionerna r , e , c , F och β med motsvarande
Laplacetransformer får vi en möjlighet att samtidigt hantera amplitud och
fördröjning. Metoden är teoretiskt elegant och i vissa sammanhang användbar
men den ställer ganska stora krav på att användaren behärskar övergången
mellan tidsfunktioner och Laplacetransformer.
Ett annat sätt att samtidigt hantera amplitud och fördröjning är att använda
komplexa tal. En signal kan delas upp i och beskrivas som en summa av
sinusformade signaler (Fourier-uppdelning). En beskrivning av hur en
förstärkare uppför sig för sinusformade signaler av olika frekvens ger
alltså en fullständig bild av hur förstärkaren uppför sig för godtyckliga
signaler. Man kan då använda komplexa tal där beloppet motsvarar
amplitud och argumentet motsvarar fasvridning. Man kan då i det
komplexa talplanet rita kurvor som visar hur förstärkningen blir vid
olika frekvenser. Om en sådan kurva omsluter punkten -1 + i0 är
förstärkaren instabil (Nyquist-kriteriet).
Ett annat sätt att formulera Nyquist-kriteriet är: Om förstärningen vid
någon frekvens ger fasvridningen 180 grader samtidigt som dess
belopp är större än 1 blir förstärkaren instabil.
Det går alltså att formulera villkor för stabilitet hos den återkopplade
förstärkaren och i många andra sammanhang kan man se att förhållandena
kan hanteras på samma sätt.
DEL 3
Hur fungerar världen?
=====================
Aristoteles (384 - 322 f Kr) gjorde en ganska omfattande sammanställning av
vad som då var känt.Han och hans efterföljare sa i princip:
Världen är vad den synes vara eller borde vara
Tunga föremål faller fortare än lätta.Stora hus är större än små och skall
alltså avbildas större.Solen och stjärnorna rör sig över himlen.Det finns
fyra aggregationstillstånd jord = fast fas , vatten = vätska , luft = gas ,
eld = plasma och kanske ett femte "de vises sten" = kollapsad stjärnmateria
och av dessa tillstånd är allt uppbyggt.
I stort sett stod sig denna uppfattning i ett och ett halvt årtusende.
Världen fungerade enligt av Gud givna lagar.Men Gud kunde bryta mot lagarna
och bistå enskilda människor.Och han var stor nog att bry sig om varje
människa.Det kunde löna sig att be om underverk,särskilt om man anlitade
prästerlig konsulthjälp.
Men tankebyggnaden började knaka i fogarna.Om man avbildade stora hus små
när de var långt borta blev bilderna mer lika verkligheten än när man
använde "korrekt" storlek.
Copernicus (1473 - 1543) visade att man fick en enklare bild av verkligheten
om man tänkte sig att jorden roterar kring sin axel och kring solen.
Galilei (1564 -1642) spädde på med att visa att man kunde se Jupiters månar
rotera kring planeten om man använde en kikare.Och han visade även att
påståendet att tunga föremål faller fortare än lätta bara gäller om de
lätta har större luftmotstånd i förhållande till sin vikt.
Påven, som såg hur fotfästet för hela världsuppfattningen höll på att gå
förlorat, försökte förgäves stoppa sådana ideer.
Newton (1642 -1727) visade att händelseförlopp kunde beräknas och förutses i
en utsträckning som man dittills inte kunnat tänka sig.Guds ingripanden
behövdes i långt mindre omfattning än vad man föreställt sig tidigare.En stor
del av förtröstan på Guds godhet kunde flyttas över på en förlitan på att
världen var förutsägbar.Gud hade skapat världen så att han mycket sällan
behövde ingripa. Världsuppfattningen fick ett nytt fotfäste.
För närobservationer använder vi känsel,hörsel,lukt,smak och syn men för fjärr-
observation är vi praktiskt taget helt hänvisade till synen.Kunskap om ljus
spelar därför en avgörande roll för vår världsuppfattning.Maxwell (1831 - 1879)
gav med den elektromagnetiska ljusteorin en mycket elegant beskrivning av ljus.
Men han väckte också en besvärlig fråga.
Maxwells ekvationer beskriver ljus som en vågrörelse mellan elektriskt och
magnetiskt fält.Men det finns ingen knytning av denna vågrörelse till ett
vågbärande medium. Vattenvågor bärs av vatten,ljudvågor bärs av luft och vi
kan definiera vågornas hastighet i förhållande till vattnet eller luften.
Och om vattnet eller luften strömmar påverkas även vågornas rörelse. Men
Maxwells ekvationer visade inte på något sådant för ljus!!
När Michelson (1852 - 1931) och Morley försökte mäta jordens hastighet
i förhållande till den ljusbärande världsetern blev resultatet noll.Liksom den
fasta jorden hade rubbats av Copernicus sviktade nu den fasta världsetern.
Einstein (1879 - 1955) hävdade att vi måste överge föreställningen att alla ser
samma värld.Om två observatörer rör sig i förhållande till varandra upplever de
att den andres klocka och meterstav påverkas av rörelsen.
Heisenberg (1901 - 1976) visade att vi inte samtidigt kan mäta tid och energi
med hur stor noggrannhet som helst.Och mätningarna påverkar vad vi mäter.Trots
att vi kommit på hur man kan bygga förstärkare som förstärker en signal till
vilken styrka som helst finns det gränser för hur noggrant man kan mäta.
Fotfästet i en av Gud given värld som är oberoende av alla observatörer sviktade.
Men om vi delar upp tidsbegreppet i koordinattid och parametertid där
koordinattid är en rumskoordinat likvärd de övriga tre och parametertiden är
en förändringsparameter då kanske vi åter kan se en eter,ett alluppfyllande
Brahma.Ett Brahma som strömmar med ljushastighet som en etervind. En etervind
som vi svävar i som ballonger eller moln som följer vinden. En vind som kan
blåsa åt olika håll i det tredimensionella rummet genom att etern är
kompressibel och/eller att etervinden i koordinattidsled kan variera. En värld
som är lika för alla betraktare men där den tredimensionella projektionen av
den fyrdimensionella världen kan variera för olika betraktare.
Vad är verklighet?
==================
Vi lever i en värld som förändras.Denna värld observerar vi med
sinnen som registrerar förändringar.
Om man sätter ett finger mot en bordsyta känner man när fingret
vidrör bordsytan.Men om man håller kvar fingret försvinner
känslan.Vårt känselsinne registrerar alltså inte kontakten med
bordsytan utan bara förändringen när fingret sätts mot bordet.
Om man håller ögonen orörliga under tillräckligt lång tid för-
svinner synintrycket.För att vi skall se något räcker det inte
med förändringarna när enskilda fotoner träffar näthinnan.Hela
mönstret i bilden måste förändras för att vi skall se något.
Vi ser inte världen sådan den är.Vi ser förändringar av världen.
Det vi upplever som verklighet är alltså inte verkligheten utan
förändringen av verkligheten.Vi ser inte verkligheten utan verk-
lighetens tidsderivata.
Bakom den verklighet vi upplever när våra sinnen registrerar
förändringar finns alltså en verklighet som förändras.
Ett föremål som ett hus kan förefalla vara en stabil oföränder-
lig företeelse men för att vi skall kunna veta att det finns
måste det förändra ljusstrålar som faller på det eller stoppa upp
vår handrörelse när vi tar på det.Våra sinnen registrerar alltså
enbart förändringar runt huset.Vi kan bara indirekt sluta oss
till att huset finns.
Våra sinnen informerar oss om förändringar i vår omvärld och vi
finner att många av dessa kan beskrivas genom att vi antar att
det finns en bakomliggande verklighet som orsakar dessa föränd-
ringar.Utifrån de förändringar vi registrerar kan vi dra vissa
slutsatser om denna verklighet men vi kan inte få veta allt om
den.
Om världen kan beskrivas av någon sorts funktion som har en tids-
derivata och om vi kan registrera tidsderivatan kan vi integrera
denna tidsderivata för att komma till ursprungsfunktionen.Men vi
vet att integration ger en obestämd integrationskonstant.Tids-
derivatan innehåller alltså inte all information om ursprungs-
funktionen.
Den värld vi upplever med våra sinnen är alltså förändringar av
en bakomliggande verklighet.Och för de flesta av oss gäller att
all vår strävan går ut på att styra dessa förändringar och
därigenom anpassa världen efter våra önskemål.
För att vi skall kunna uppfatta något måste världen innehålla
företeelser som avviker från omgivningen (kvanta) och dessa måste
bilda händelser genom att ändra läge i förhållande till varandra.
Vi kan inte se kvanta bara händelser.
För att observera något måste vi förändra det vi observerar. Det
är bara genom att se hur det förändras som vi kan dra slutsatser om
hur det ser ut. Vi kan inte komma fram till "das Ding an sich", till
verkligheten sådan den är. Vi kan bara föreställa oss en verklighet
som förändras på det sätt som vi observerar.
Ju noggrannare vi mäter ju mer förändrar vi det vi mäter. Om vi vill
veta allt om hur stenarna ligger i ett tegelhus måste vi plocka bort
alla stenar och förändra huset till en tegelstenshög. Men så brukar
vi inte göra. Vi nöjer oss med att se ytan på ytliga stenar och
kanske plocka bort ett par stycken. Så antar vi att övriga stenar
ligger på samma sätt, d v s att mönstret upprepas. Det mesta av vår
världsuppfattning bygger på denna föreställning om mönsterupprepning.
Vi föreställer oss en värld där mönster upprepas som tapetmönster. En
värld där förändringar kan inträffa och bilda händelser som vi kan
registrera med våra sinnen så att vi kan dra slutsatser om hur mönstren
ser ut.
Denna mönsterupprepning är ett av de största mysterierna. Vi vet inte
varför det är så och mycket lite om de regler som den följer.
Plancks konstant - Alltets konstant
===================================
Betrakta ett universum som innehåller h stycken urskiljbara kvanta. Varje
sådant kvanta är så litet att det inte går att dela. Det kan bara finnas
eller inte finnas. Vi kan kalla ett sådant kvanta för enhetskvanta eller
på engelska unit-quanta och beteckna det med UQ. Sorten för h blir alltså UQ
Den minsta händelse som kan inträffa i detta universum är minsta detekterbara
lägesförändring för ett enhetskvanta i förhållande till övriga kvanta. En
sådan händelse kan vi kalla för enhetshändelse eller på engelska unit-event
och beteckna med UE.
Alla händelser kan delas upp i enhetshändelser men en enhetshändelse kan inte
delas upp. Den 'inträffar' eller 'inträffar icke'. Något däremellan finns inte.
Totala antalet enhetshändelser som någonsin inträffat i vårt universum kallas
för absolut tid ( egentligen absolut parametertid). Tidpunkten för en viss
händelse är totala antalet enhetshändelser som inträffat före händelsen.
Tiden mellan händelse A och händelse B är tidpunkten för händelse B minus
tidpunkten för händelse A. Tid betecknas med τ och sorten för tid blir
alltså UE.
Antag att vi intresserar oss för en viss del av vårt universum, t ex av en
kula. Av alla kvanta i universumet avgränsar vi då några som utgör kulan. Vi
kan beteckna dessa kvanta med E. Med E menar vi alltså ett visst antal
enhetskvanta och sorten för E blir alltså UQ. Då gäller att E/h anger hur
stor del av universum som kulan utgör.
Om det så inträffar en enhetshändelse är sannolikheten E/h att denna
enhetshändelse består i att något av de kvanta som utgör kulan ändrar läge.
På tiden τ inträffar τ enhetshändelser och varje gång är sannolikheten
E/h att något av de kvanta som utgör kulan ändrar läge. I uttrycket
τ E
a = -----
h
är alltså a det antal gånger som ett enhetskvanta som ingår i E ändrar läge
under tiden τ. Om man minskar τ och/eller E så att a blir mindre än ett
övergår a till att ange sannolikheten att något kvanta inom E ändrar läge under
tiden τ.
τ E UE UQ
Sorten för a = ----- blir ----------- d v s UE.
h UQ
Om vi avgränsar en så liten mängd kvanta ΔE och observerar den under så kort
tid Δτ att Δτ ΔE = h/2 kommer endast en halv enhetshändelse att
beröra ΔE d v s sannolikheten att någon händelse inträffar som berör ΔE blir
0,5. Detta är gränsen för att vi skall kunna se att något händer med ΔE.
(Heisenbergs osäkerhetsrelation).
Låt oss se på ett litet universum med h = 1000 UQ där vi avgränsar en kula
med E = 10 UQ. Det är då bara var hundrade UQ som tillhör E. Det är alltså
bara var hundrade enhetshändelse som innebär att något kvanta i E har
flyttats. Efter en förändring av E går det alltså 100 UE innan det på nytt
är dags för en förändring av E. Vi säger att E:s periodtid är 100 UE.
Periodtid betecknas T och har sorten UE. För att bestämma periodtiden
sätter vi a = 1 i uttrycket τ = a h/E och får alltså T = h/E. Egentligen
är alltså T = 1 h/E där 1 har sorten UE så att även T får sorten UE.
Inverterade värdet av periodtiden kallas för frekvens.
Frekvens betecknas f och har sorten UE-1. Frekvensen för E är
f = E/h alltså egentligen f = E/(1 h) där ettan har sorten UE.
h är alltså antalet enhetskvanta i hela universum. Sorten för h är alltså UQ.
Men h är också det antal enhetshändelser som erfordras för att rubba samtliga
enhetskvanta i universum. Ser vi det så har h sorten UE. Och om en viss
enhetshändelse inträffar är h det antal enhetshändelser som troligen inträffar
innan den upprepas. Även om vi ser h på det viset blir sorten UE.
Även om alltså sorten för h inte är helt entydig är värdet entydigt för ett
visst universum. För alla i vårt universum har h samma värde. Men trots det
har vi ingen bra metod att fastställa detta värde. Vi vet inte exakt hur stort
vårt universum är och därmed vet vi inte heller det exakta värdet på h. Vi har
alltså inget bra värde på h varken i sorten UQ eller UE. Om vi vill kan vi
emellertid vända på resonemanget och säga att vi mycket väl vet värdet på h
men vi vet inte hur stort ett enhetskvanta är och därför kan vi inte uttrycka
h i sorten UQ.
Vi använder inte enheterna UQ ch UE för att ange kvantamängder och tider.
Detta beror dels på att det skulle bli svårhanterligt stora tal dels på att
vi inte exakt kan fastställa storleken på ett UQ och på en UE. Vi använder
i stället sorter som Joule och sekund som är ett stort antal UQ resp UE.
På en sekund går det ett visst antal (ks) enhetshändelser. På en
Joule går det ett visst antal (kJ) enhetskvanta. För att avgöra
vad som händer med värdet på h om vi övergår till att ange τ i sekunder
och E i Joule kan vi utgå från uttrycket τ E = a h. Om vi övergår till
sekunder och Joule får vi
τ ks E kJ = a h
a h
τ E = --- ---
ks kJ
Vi bibehåller sorten UE för a och får då
h i Js lika med (h i UQ)/(ks kJ)
Sorten för h är inte entydig eftersom ett enhetskvanta under vissa
omständigheter motsvaras av en enhetshändelse. h får då samma värde
oberoende av om vi använder sorten UQ eller UE. Men använder vi i
stället sekund och Joule måste omräkningsfaktorerna komma på rätt
plats och vi får då entydigt sorten Js för h.
h kallas för Plancks konstant.
Bortom tid och rum
==================
När vi som barn blir medvetna om vår omgivning börjar vi fråga "Vad
finns bortom?" , "Vad fanns före?" och "Vad kommer efter?".Och varje
gång vi får ett svar förskjuter vi gränserna för den värld vi upplever
som känd och ställer på nytt samma frågor.
Till slut brukar vi bli avspisade med att frågorna är meningslösa och
att ingen kan svara på dem.Men så är det faktiskt inte.Vi kan faktiskt
ibland hitta absoluta gränser.Det kanske mest iögonfallande exemplet är
absoluta nollpunkten för temperatur.
När man upptäckte att gaser ökade tryck och/eller volym när man värmde
dem fick man ett sätt att mäta temperatur.Vår instinkt att fråga "Vad
finns bortom?" ledde till att man började fundera kring frågan "Hur
kallt kan det bli?".Och svaret var faktiskt inte "Hur kallt som helst".
Om man kylde en gas vid konstant tryck minskade dess volym.Men till slut
kom man till volymen noll.Och eftersom vi inte kan tänka oss vad negativ
volym skulle kunna vara insåg man att det finns en absolut nollpunkt för
temperatur.
När vi tittar på en avlägsen stjärna tittar vi inte bara långt bort, vi
tittar även bakåt i tid.Vi ser inte stjärnan sådan den ser ut nu utan
sådan den såg ut när ljuset lämnade den. Om solen plötsligt slocknade
skulle vi inte märka något förrän det gått 8 minuter. Fram till dess
skulle ljus som var på väg mot oss när den slocknade fortsätta att komma
fram. Vi ser alltså inte solen sådan den är utan solen för 8 minuter
sedan.Och avlägsna stjärnor kan vi se för miljarder år sedan.
Liksom man en gång i tiden undrade hur kallt det kunde bli kan vi fråga oss
hur långt och hur långt tillbaka vi kan se. Och även här är faktiskt inte
svaret "Hur långt som helst".
Ljus kan uppfattas som en vågrörelse och färger som frekvensen hos denna
vågrörelse. Blått ljus har hög frekvens och rött ljus har lägre frekvens.
Vitt ljus är en blandning av olika färger d v s av olika frekvenser men
blandningen är inte jämn. Frekvenserna är koncentrerade till s k
spektrallinjer som motsvarar egenskaper hos de ämnen som avgivit ljuset.
Spiller man lite saltvatten i lågan på en gasspis lyser lågan med en gul
färg som motsvarar en kraftig spektrallinje hos det natrium som ingår i
saltet.
När vi tittar på ljus från fjärran stjärnor finner vi att färgen har
förskjutits mot rött. Och det är inte fråga om en omfördelning av
färgintensiteter för alla spektrallinjer har fått lägre frekvens. Det är
alltså så att ljusets frekvens blir lägre ju längre bort vi tittar.
Det innebär att om vi tittar tillräckligt långt bort blir ljusets frekvens
noll.
Och liksom vi inte kan tänka oss en negativ volym kan vi inte tänka oss en
negativ frekvens. Vi kan alltså inte ha större avstånd än att ljuset som når
oss från det avståndet får frekvensen noll. Och vi kan inte ha längre tid
tillbaka än gångtiden för ljus som når oss från detta avstånd.
Hur ser då världen ut när vi kommer till största möjliga avstånd? Vi "ser"
där en värld som avger ljus med frekvensen noll d v s totalt mörker. En
värld där vi inte kan urskilja någonting. Där vi inte kan skilja två punkter
från varandra och alltså inte tala om deras läge och avstånd. En värld där
vi inte kan urskilja punkter så att vi kan säga att en händelse har inträffat
genom att deras läge har förändrats. En värld utan avstånd och utan händelser
d v s en värld utan rum och tid.
Man brukar uppskatta det största möjliga avståndet till mellan 10 och 20
miljarder ljusår och motsvarande tid blir alltså mellan 10 och 20 miljarder
år.
Rum och tid är alltså ändliga begrepp som endast har mening lokalt i den
värld där vi råkar befinna oss. Utanför denna världs rum och tid råder en
jämn fördelning, d v s ett totalt mörker där allt överallt är lika. Vi
kommer ur ett totalt mörker, vi går mot ett totalt mörker och vi omges
av ett totalt mörker. Men den störning av detta perfekta tillstånd som
vi kallar världen är tillräckligt stor för att vi skall kunna ha en hel
del skoj på vägen.
Tid
===
En stillastående värld är ointressant.
Det finns en gammal film,jag tror den hette "A kind of stopwatch" om en man med
ett stoppur som har den egenskapen att när han startar det stannar allt i hela
världen utom han själv.Han använder det för att plundra en bank där han i lugn
och ro kan gå omkring bland stillastående kunder och tjänstemän.Men när han skall
trycka igång världen igen tappar han uret i golvet så att det går sönder och han
blir fast i en meningslös stillastående värld.
Lyckligtvis står vår värld inte stilla.Den är stadd i ständig förändring.
För att få ett mått på världens förändring kan vi dela in den och se den som
summan av en massa små händelser.
Den minsta händelse vi kan observera innebär att någon urskiljbar punkt
förändrar sitt läge i förhållande till övriga urskiljbara punkter med den
minsta detekterbara lägesförändringen.Vi kan kalla en sådan händelse för
en enhetshändelse.Så kan vi dela in världens förändring i enhetshändelser
(det blir ett stort och ohanterligt tal men det blir ett ändligt tal).
Enligt föregående avsnitt kan vi finna en gräns för hur långt tillbaka vi
kan gå och vi kan alltså finna en siffra som anger totala antalet
enhetshändelser sominträffat i vår värld.Siffran blir stor och vi har inte
mätmetoder som gör att vi kan bestämma den särskilt noggrant men vi kan
konstatera att denna siffra finns och vi kan kalla den för "absolut tid".
Vi kan uppskatta den absoluta tiden till att nu vara c:a 15 10120
enhetshändelser.
Det finns en mängd olika uppskattningar av Hubble-konstanten men låt oss
anta att universums ålder är 15 miljarder år och radien 15 miljarder ljusår.
Medeltätheten kan uppskattas till 4 10-26 kg/m3. Vilket innebär att
totala innehållet är 2 1053 kg eller 2 1070 J.Om vi dividerar med Plancks
konstant får vi motsvarande frekvens som alltså blir 3 10103 Hz.
Inverterar vi det värdet får vi periodtiden som vi kan använda som mått på
kortast möjliga tid d v s som mått på den tid som åtgår för en enhetshändelse.
Vi får alltså fram att det går 3 10103 enhetshändelser på en sekund och
att en enhetshändelse tar 3 10-104 s.Då 15 miljarder år är 5 1017 s
innebär det att den absoluta tiden nu är c:a 15 10120 enhetshändelser
Men även om vi inte kan bestämma den absoluta tiden särskilt noggrant och även om
den absoluta tiden blir ohanterligt stor kan vi,med stor noggrannhet,mäta tiden
mellan två händelser som inträffar inom vårt observationsområde.
Av alla händelser som inträffar i universum är de allra flesta helt slumpmässiga.
Det är bara en mycket liten del som vi kan påverka.Men enhetshändelser har en
tendens att bilda mönster och samordnas till större händelser som vi kan
observera.Eftersom sådana inträffar helt slumpmässigt kan vi utgå från att om
vi nöjer oss med att observera en viss typ av händelse inom ett litet område så
får vi ett mått på totala antalet händelser.Vi kan t ex bygga ett pendelur och
räkna med att varje gång händelsen att pendeln fullbordat ett slag har inträffat
har det gått en sekund d v s har det inträffat 3 10103 enhetshändelser i hela
universum.Att den andel av det totala antalet händelser som vi mäter på detta sätt
är konstant kan vi övertyga oss om genom att göra två likadana klockor och se
om de går likadant.Vi finner då att om vi kan isolera dem från störande
inverkan utifrån går de nästan exakt lika.
Rum
===
På liknande sätt som vi kan definiera en enhetshändelse kan vi definiera en
enhetslängd.En enhetslängd är helt enkelt den sträcka ljuset hinner gå under en
enhetshändelse.
Vårt universum blir då ett rum i form av ett klot med radien 15 10120 enhetslängder.
Detta klot kan vi dela in i enhetsceller med en enhetslängd som sidlängd.Detta
klot rymmer alltså c:a 1 10364 enhetsceller.
Om vi även vill räkna in alla enhetsceller som någonsin funnits får vi betrakta
tid som en fjärde dimension.Vi får då ett fyrdimensionellt halvklot med c:a
1 10485 enhetsceller.
En enhetscell ligger på gränsen till att vara observerbar.Det går alltså inte att
urskilja några detaljer i den.Vi kan bara skilja mellan om den innehåller något eller
om den är tom.Vi kan alltså fullständigt beskriva den med en etta eller en nolla.
Världen är alltså ett "datorminne" som rymmer 10364 bits och som totalt
har hanterat 10485 bits.
Med "avstånd" mellan A och B menar vi det antal enhetsceller vi måste passera för att
komma från A till B.
Vi kan alltså se på världen som en dator med ett enormt minne.Men en dator är
praktiskt taget oanvändbar om den inte har ett operativsystem som gör att innehållet
i minnet ändras enligt vissa regler.Och även världen har sitt "operativsystem".Hur
detta fungerar är vad fysik egentligen handlar om.
Orsak och verkan
================
För att bli användbar behöver en dator något operativsystem med någon form av BIOS
(Basic In/Out System).Ännu mer fundamentalt är att man redan i processorns hårdvara
brukar lägga in vissa begränsningar av hur minnet kan förändras.Man brukar t ex
dela in minnet i grupper om 8 , 16 eller 32 bits som hanteras samtidigt.
För att kunna använda datorn måste vi komma fram till en förenklad uppfattning av
den,en uppfattning som är användbar och som kan rymmas inom vår tankeförmåga.Vi
börjar då med att bortse från ettor och nollor för att i stället se grupper av
bits som vi kallar bytes.
På liknande sätt finner vi att världen har ett "BIOS" som grupperar enhetsceller.
Sammanhängande grupper av enhetsceller kallar vi partiklar och vi finner att det
finns förvånansvärt stabila sådana.Av någon anledning förblir mönstret av ettor
och nollor inom en partikel ofta konstant även om partikeln ändrar läge i
förhållande till andra partiklar.
Ett sätt att se detta bevarande av mönster är att jämföra med ballonger i
byig vind. Dessa flyttas av vindbyar så att de ändrar läge i förhållande till
varandra men om ballongerna ligger tätt kommer inte en vindby att ändra det
inbördes läget för närliggande ballonger.
Även i tidsled grupperar världens "BIOS" enhetshändelser till händelsekedjor som
bildar urskiljbara mönster.Om vi vet vad som har hänt kan vi,i vissa fall,förutse
vad som kommer att hända.Om vi vet att en partikel har förflyttat sig i ett område
med enbart nollor kan vi förutse att den kommer att fortsätta förflyttningen.
Vi kallar den förflyttning som redan skett för orsak och den som vi förutser för
verkan.
Vi har funnit ett antal orsak-verkan-samband som vi kan använda som ett sorts
högnivåspråk för programering av världen.Om vi önskar en viss verkan men finner
att den är svår att uppnå kan vi leta bland dessa samband för att se om vi i
stället kan finna en orsak som är lätt att åstadkomma och som ger önskad verkan.
Eller en orsak som har en verkan som kan vara orsak till den önskade verkan.Eller
en orsak till en orsak till en orsak till verkan.
Människor har naturligtvis alltid använt sig av orsakskedjor för att nå sina mål.
Men till en början skedde detta huvudsakligen intuitivt.Att orsaka en spräckning
av ett flintstycke så att man får en användbar flintkniv är en konst som våra
förfäder utvecklade och förfinade.Man lärde sig orsakskedjorna men man
verbaliserade dem inte.Lärlingen lärde sig huvudsakligen genom att se och höra
mästarens slag och genom att själv slå med slagsten på flinta.
Kring mitten av det gångna årtusendet började en målmetveten strävan att
verbalisera orsak-verkan-samband.Detta lyckades över förväntan och så sent som
under adertonhundratalets slut trodde man på fullt allvar att varje verkan
kunde knytas till orsaker som i sin tur kunde knytas till orsaker.
Kvantfysiken och speciellt Heisenbergs osäkerhetsrelation bröt med denna
föreställning genom att hävda att ett orsak-verkan-samband säger att en orsak
innebär en viss sannolikhet för en viss verkan.Denna sannolikhet kan vara nära
ett men den är alltid mindre än ett.
Om man släpper en sten är sannolikheten stor att den faller nedåt.Men det finns
en liten,beräkningsbar,sannolikhet att den faller uppåt.Denna sannolikhet är
naturligtvis så liten att vi,för praktiskt bruk,kan strunta i den.Men att den
finns är principiellt viktigt för det innebär att världen kan komma med
överraskningar.
Heisenbergs osäkerhetsrelation bygger på insikten att världen både har partikel-
karaktär och vågkaraktär samtidigt.Men en våg måste observeras under åtminstone
större delen av periodtiden innan man kan veta att det verkligen rör sig om en
våg.En ansamling fyllda enhetsceller,d v s en ansamling ettor,kan bilda en
partikel.Ju fler ettor den innehåller ju högre säger vi att dess energi är.
Och när vi använder vågbeskrivning blir dess frekvens energin dividerad med
Plancks konstant.Ju högre energi den har ju högre frekvens och därmed kortare
periodtid har den.
Något förenklat kan man säga att Heisenberg påpekade att man måste observera
en energimängd under halva dess periodtid innan man säkert vet om den finns.
Om man vill veta hur stor en energimängd är och när den har denna storlek måste
man göra en nogrann mätning under kort tid.Men ju noggrannare man vill veta
hur stor den är ju längre tid tar mätningen.Och ju mer exakt man vill veta
mättidpunkten ju sämre hinner man mäta energiinnehållet.
Heisenberg konstaterade att om man samtidigt försöker mäta två storheter A och B
som har egenskapen att deras produkt har sorten Js så blir minsta möjliga fel
ΔA ΔB = h/2
där h = Plancks konstant.
Energi
======
Enhetshändelser inträffar och bildar mönster i form av händelsekedjor.Sådana
händelsekedjor kallar vi händelser.Händelser inträffar hela tiden.Dessa
händelser är helt enkelt tiden.
Av alla händelser som inträffar är det en mycket liten del som vi kan
förutse och påverka.Men hur liten den delen än är är den viktig för oss.Så
viktig att vi behöver ett särskilt begrepp för den.Vi kallar förutsebara,
påverkbara händelser för energi.
Det förefaller som om vi inte kan tömma eller fylla en enstaka enhetscell.
Vi kan alltså inte göra om en etta till en nolla eller tvärtom.Däremot kan
ettor byta plats med nollor.Så vitt vi vet består alla händelser vi observerar
i att ettor och nollor byter plats.Världens BIOS tycks se till att minnet hela
tiden har lika många ettor.
Nollor är mycket vanligare än ettor i vår värld.Om vi påträffar en fylld
enhetscell,d v s en etta,kan vi alltså förutse att den kommer att bytas ut mot
en nolla.De ettor vi observerar är alltså förutsägbara förändringar d v s
förutsägbara och därmed påverkbara händelser,d v s energi.
Den tätaste materia vi känner är den som finns i kollapsade stjärnor.Om vi
antar att denna materia består av enbart ettor kan vi uppskatta andelen ettor
i vår del av världen.En uppskattning av denna täthet är 3 1010 kg/m3.
Medeltätheten i vår del av världen rör sig om 4 10-26 kg/m3.
Förhållandet mellan dessa tätheter utgör ett mått på andelen ettor i vår värld.
Det går alltså c:a 1036 nollor på varje etta.
Även i den tätaste materia vi känner här på jorden går det mer än en miljon
nollor på varje etta.
En enhetshändelse innebär alltså att en etta och en nolla byter plats.Eftersom
antalet ettor är så mycket mindre än antalet nollor är det antalet ettor som
anger hur ofta detta sker.Antalet ettor inom en viss volym anger alltså hur
många förutsebara händelser som kommer att inträffa i volymen d v s hur stor
energi som finns i volymen.
Om man kan avgränsa en viss volym så att den inte kan utbyta ettor mot nollor
eller tvärsom över volymgränsen blir antalet ettor d v s energin konstant inom
volymen.
Detta brukar kallas för termodynamikens första huvudsats och formuleras som att
energin hos ett slutet system är alltid konstant.
Men en enhetshändelse är mycket liten,så liten att vi inte känner något sätt att
utnyttja en enstaka enhetshändelse.Att försöka finna en enstaka etta för att
kunna utnyttja att vi kan förutse att den kommer att bytas ut mot en nolla är
som att försöka manipulera gener med grävskopa.Våra sinnen,instrument och verktyg
är trubbiga och vi behöver enhetshändelser som sker samordnat till användbara
händelser.Om vi avgränsar en viss volym så att den bildar ett slutet system
kan det hända att fördelningen av ettor inom systemet är ojämn.Vi kan t ex
ha många fler ettor i ett hörn än i resten av volymen.Vi kan då,inte bara förutse
att varje etta kommer att bytas mot en nolla,vi kan förutse att sådana byten
kommer att ske oftare i detta hörn än i resten av volymen.Och detta kan ske i
en skala som vi kan använda.En sned fördelning av ettor inom ett slutet
system kan vi alltså använda.Men det är användbart därför att vi kan förutse
att fördelningen kommer att utjämnas och när vi använder det utjämnas för-
delningen och blir oanvändbar.
Detta brukar kallas för termodynamikens andra huvudsats.Den formulerades i en
tid när man främst var intresserad av att omvandla värme till arbete och när man
fann att man måste ha en sned temperaturfördelning för att omvandla värme till
arbete.Den brukar därför formuleras:Entropin (värmelärans motsvarighet till
ellärans laddning eller mekanikens tyngd) hos ett slutet system kan inte
minska.
En konsekvens av andra huvudsatsen är att tiden bara går åt ett håll.I stället
för att säga "Entropin hos ett slutet system kan inte minska" skulle vi kunna
säga "Tiden kan inte minska".
När vi var små spelade min bror och jag ibland schack.Det hände att vi hamnade
i lägen där vi inte kunde komma på vad vi skulle göra härnäst.Jag kunde då
flytta tornet ett steg för att i nästa drag återgå till utgångsläget och han
kunde göra likadant.Så kunde vi "spela" hur länge som helst utan att ställningen
förändrades.Spelet gick bara framåt av irreversibla drag t ex flyttning av en
bonde,att någon slog en pjäs eller att någon gjorde ett drag som öppnade nya
möjligheter.
Om en etta byter plats med en nolla går tiden fram en enhet.Men om nästa
enhetshändelse är att ettan återgår till utgångsläget går tiden bakåt en
enhet.Ingen kan veta att något har hänt.Alla minnen består av enhetsceller
och för att någon skall kunna minnas en händelse måste den orsaka en
händelsekedja som ställer om något minne.
Liksom schackspelet går tiden bara framåt av händelser som är eller som på
grund av andra händelser blir irreversibla.
När man började studera möjligheter att omvandla värme till arbete fann man
att man vanligen utgick från värme med hög temperatur och liten entropi för
att sluta med en rest av värme vid omgivningstemperatur med högre entropi
än utgångsvärmet.Entropiökningen innebar att man inte kunde komma
tillbaka till utgångsläget. Man började därför betrakta entropi som ett mått
på irreversibilitet.Och begreppet används idag i vidgad betydelse så att
man t ex vid kemiska reaktioner talar om en entropiterm som anger
reaktionens grad av irreversibilitet även om det inte direkt är fråga om
en omvandling till värme.
Med denna vidgning av begreppet blir alltså entropiökning en synonym till
tidökning.Och andra huvudsatsen utsäger det vi alla av erfarenhet vet,
nämligen att tiden bara går åt ett håll.
Termodynamikens första och andra huvudsatser är viktiga regler som vi kan
använda när vi försöker utnyttjas världens BIOS.Men utöver dem finns det andra
hinder för utjämning mellan ettor och nollor.Möjligheten att avgränsa slutna
system innebär att det finns möjligheter att "låsa in" ettor i avgränsade
volymer där utjämning med omgivningen inte sker trots att den borde göra det
enligt första och andra huvudsatsen.Vi har t ex inte funnit något sätt
att få materia att restlöst omvandla sig till andra energiformer trots
att första och andra huvudsatsen säger att det borde vara möjligt.
Arbete
======
Antag att jag skall lyfta en säck mjöl.
Jag skall då genomföra den procedur som inom datatekniken kallas för shift.
Via världens BIOS anropar jag shift-proceduren för alla de bits som utgör
säcken.Detta anrop omfattar en lång och komplicerad händelsekedja men på
samma sätt som en dators operativsystem gömmer programelement för operatören
är denna kedja okänd för mig.Jag vet bara att jag anropar shift-proceduren
genom att ta tag i säcken och lyfta.
När alla de bits som utgör säcken skiftats mot ovanförliggande bits har säcken
lyfts en enhetslängd och det är bara att anropa shift-proceduren på nytt och
på nytt tills jag fått upp den tillräckligt.
Jag finner nu att det krävs en viss viljeansträngning för att jag,på detta
sätt,skall anropa shift-proceduren.Utförande av något som kräver viljeansträng-
ning kallar vi arbete.Här på jorden är det tydligen så att det krävs arbete
för att lyfta föremål.Att lyfta är en typ av förflyttning och jag finner att
även andra typer av föremålsförflyttning kan kräva arbete.Inom fysik gör man
den förenklingen att man enbart talar om sådant arbete som är knutet till
förflyttning av föremål.
Om jag provar att lyfta olika säckar till olika höjd finner jag att det krävs
mer arbete att lyfta en säck ju högre jag lyfter den och det krävs mer arbete
ju mer det är i den.Åker jag till månen finner jag också att det krävs mer
arbete att lyfta en viss säck till en viss höjd på jorden än på månen.
Shift-proceduren innebär ju en förutsägbar och avsiktlig förändring.Den är
alltså energi.Arbete i fysikalisk mening är alltså en form av energi.Men även
om det krävs lika mycket energi,d v s arbete,för att lyfta en lätt säck till
hög höjd som att lyfta en tung säck till låg höjd är dessa procedurer olika
och vi behöver metoder att beskriva dem som visar hur de skiljer sig från
varandra.
Vi gör då en uppdelning i
Antal ettor som skall skiftas
En faktor som anger hur svårt det är att skifta på den plats man är
Antal shift-procedurer som krävs
Vi säger att
W = mg h
där
W = det arbete,d v s den energi,som krävs för lyftet (Work)
m = säckens massa d v s antalet ettor som ingår i säcken
g = gravitationskonstanten som är olika på jorden och på månen
h = lyfthöjden,d v s antal erforderliga shift-procedurer
Produkten mg kallar vi säckens tyngd.
Vi delar alltså upp energin i två faktorer där den ena (tyngden) anger hur stor
mängd vi arbetar med.Vi kallar denna faktor för extensiv faktor eller mängdfaktor.
Den andra faktorn anger hur stor förändring varje del av mängden utsätts för.Vi
kallar den faktorn för intensiv faktor.
För min mjölsäck är alltså tyngden (mg) extensiv faktor och lyfthöjden (h)
intensiv faktor.
Kraft
=====
Vi säger att mjölsäckens tyngd är en kraft.För att åstadkomma denna anropar
jag shift-proceduren via världens BIOS.Men jag finner att jag behöver göra
likadana anrop i en rad andra fall.Om jag skall dra ett föremål över ett
strävt underlag,om jag skall sätta fart på en sten för att kasta den,om
jag skall dra en båt i vatten måste jag göra likadana proceduranrop.Vi
kallar alla sådana anrop för kraft oavsett om vi åstadkommer dem själva
eller om vi utnyttjar någon maskin för att göra dem.
Att anbringa en kraft på ett föremål är en uppmaning till föremålet att
förflytta sig.Om det förflyttar sig sker en förändring d v s energi omsätts.
Kraften gånger förflyttningslängden är den omsatta energin.
För att kunna räkna med krafter behöver vi något hanterligt mått på dem.
Vi använder oss då av den regel i världens BIOS som säger att om ingenting
bromsar rörelsen kommer en kraft som verkar på en massa att öka dess hastighet.
Vi kallar den kraft som varje sekund ökar hastigheten hos en massa på 1 kg med
1 m/s för 1 N (Newton).Vi har alltså att
1 N = 1 kg m/s2
Vi använder oss av krafter för att åstadkomma önskade förändringar där och när
vi vill ha dem.Men förändringar inträffar också hela tiden spontant.Om vi vill
åka med ett luftskepp från Stockholm till Göteborg startar vi en drivmotor som
ger en kraft som förflyttar skeppet mot Göteborg.Denna kraft gånger den väg vi
färdas är det arbete,d v s den energi,som vi måste tillföra.Men det är viktigt
att observera att denna energitillförsel inte är nödvändig för att vi skall
komma till Göteborg i och för sig.Den är nödvändig för att vi skall kunna
förutsäga när vi kommer till Göteborg.Om vi lät skeppet driva omkring i luft-
havet i oändlig tid skulle vi naturligtvis,förr eller senare,hamna över
Göteborg och då skulle vi alltså ha fullbordat resan.Men det är ett mycket
opraktiskt sätt att resa.Vi behöver åtminstone någon typ av kraft som gör att
vi kan förutsäga färdvägen lite bättre.
Brus
====
Värme är slumpmässiga molekylrörelser (eller strålningsvärme). I en gas far
molekylerna omkring samtidigt som de roterar. I ett fast ämne vibrerar
molekylerna kring sina jämviktslägen.
Om man, med allt större noggrannhet försöker bestämma läget hos ytan av ett
stycke fast materia kommer man så småningom till problemet att det inte går
att komma längre därför att de atomer som utgör ytan hela tiden rör sig.
Om man observerar en liten partikel som svävar i en vätska finner man att
den rör sig med knyckiga slumpmässiga rörelser (Browns rörelse) som beror
på kollisioner med vätskemolekyler.
Kollisioner kan även medföra att elektroner slås ut från sina lägen i
elektronskalen vilket ger en slumpmässigt varierande spänning, d v s ett
elektroniskt brus.
När man i teleteknikens barndom försökte signalera över allt större avstånd
genom att förstärka den mottagna signalen med allt högre förstärkning fann
man att man inte bara förstärkte signalen utan också ett brus. Och när
signalen drunknade i bruset kunde man inte komma längre genom att öka
förstärkningen.
Slumpmässiga, d v s oförutsägbara, händelser inträffar. Det är bara en liten
del av alla händelser som är förutsägbara genom att de har en känd orsak.
Även när det finns en känd orsak kan det finnas oförutsägbarhet om detaljer i
verkan. Värme är en orsak till molekylrörelse men hastighet och riktning för
en enskild molekyl är oförutsägbar.
Temperatur är ett mått på variansen på molekylhastigheten. Om variansen är
skiljd från noll kan vi förutsäga att en viss molekyl kommer att röra sig men
det säger ingenting om åt vilket håll och det ger bara en antydan om hur
fort den kommer att röra sig.
För en ideal gas gäller
m s2 = 3 k T
där
m molekylens massa i kg
s2 variansen på den slumpmässiga molekylhastigheten
k Boltzmanns konstant
T absoluta temperaturen i K
Styrkan hos en signal avtar med avståndet (i tid och/eller rum) från orsaken.
Bruset beror på temperaturen hos bakgrunden och temperaturen hos mottagaren.
Med ökande avstånd kommer således signalen så småningom att drunkna i bruset.
Våra förutsägelser blir alltså alltmer osäkra.
Vi kan t ex göra väderprognoser baserade på dagens kända orsaker till väder-
förändringar men bruset genererar hela tiden oförutsägbara orsaker till
förändringar och allteftersom tiden går kommer dessa allt mer att dominera
över dagens kända orsaker.
Allt vi gör är alltså förgängligt. Vilken verkan vi än åstadkommer kommer den
så småningom att drunkna i de slumpmässiga förändringar som bruset orsakar.
Den fyrdimensionella världen
============================
Med avståndet mellan punkterna A och B menar vi det minsta antal enhetsceller
man måste passera för att komma från A till B.På liknande sätt kan man
definiera tidsavståndet mellan händelserna a och b som det antal enhetshändelser
som inträffar mellan a och b.
Ett sätt att hantera avstånd mellan ett stort antal punkter är att lägga in dem
i ett treaxligt koordinatsystem.I stället för att ange alla möjliga avstånd kan
vi då ange alla punkters koordinater och ur dessa beräkna de avstånd vi vill
veta.
Det ligger nära till hands att lägga till en koordinataxel och använda den för
att ange tidskoordinat.Med avstånd i ett sådant fyraxligt koordinatsystem menar
vi då,inte bara antal enhetsceller mellan A och B utan också antal enhetshändelser
mellan att vi utgår från A och kommer fram till B.
Om vi använder ett sådant fyraxligt koordinatsystem kan vi ge tid två olika
betydelser.Vi kan dels tala om tid som en förändringsparameter.Vi kan kalla
detta för parametertid.Och vi kan tala om tid som en lägeskoordinat i vår
fyrdimensionella värld.
Så kan vi naturligtvis göra men normalt växer parametertiden och koordinattiden
likadant.Finns det då någon anledning att skilja på begreppen?Finns det något
i världens BIOS som går att beskriva genom att vi skiljer på begreppen?
Världens BIOS uppför sig faktiskt som om det fanns något som strömmade med viss
hastighet åt något håll i den fyrdimensionella rymden.Vi har inget bra namn på
detta något.Det har kallats världseter eller Brahma men låt oss för enkelhets
skull kalla det för eter.
Om allt står stilla i rummet strömmar etern i tidsriktning.Och hastigheten blir
c = t/τ
där
c = eterns strömningshastighet d v s ljushastigheten
t = koordinattid
τ = parametertid
Allt står då stilla i rummet och följer med en eter som strömmar i tidsled.
Om något rör sig i rummet kan vi uppfatta detta som att hastigheten där ändrar
riktning.Om något föremål flyttar sig sträckan s på parametertiden τ säger vi
att det rör sig med hastigheten v enligt
v = s/τ = c sin(α)
där
α = vridningsvinkeln för föremålets hastighetsvektor
Man kan uppfatta ljus som en ström av partiklar,fotoner,som rör sig med ljus-
hastighet i rummet.Fotonernas hastighetsvektor har alltså vridits 90 grader så
att de rör sig i rummet men står stilla i tiden.
Om man,likt Munchhausen,kunde hoppa ombord på en foton och titta bakåt skulle
man se startplatsen sådan den såg ut när man startade.Alla klockor på startplatsen
skulle då stå stilla.Man skulle inte röra sig i startplatsens tidsled.Men man
skulle röra sig med ljushastighet i någon annan riktning som man själv skulle
uppfatta som tidsriktningen och de som var kvar på startplatsen skulle kalla en
rumsriktning.
Gravitation
===========
Betrakta två partiklar A och B på avståndet ab.
I fig 1 anger den blå ytan alla punkter som ligger närmare A än vad B gör.Och
den gula ytan anger punkter som ligger längre ifrån A än vad B gör.Om nu B
rör sig helt slumpmässigt i förhållande till A finns det uppenbarligen många
fler punkter dit B kan gå för att öka avståndet till A än punkter dit B kan
gå för att minska avståndet.
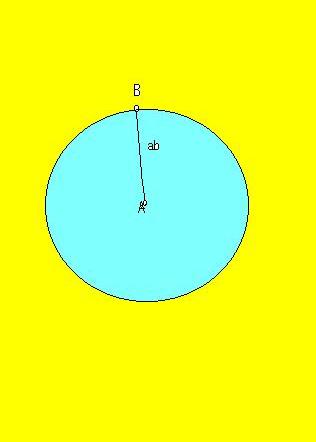 Fig 4
Sannolikheten att avståndet ökar är alltså större än sannolikheten att det
minskar.Partiklarna kommer alltså att uppföra sig som om de stötte bort varandra.
Vi kan uppfatta detta som en utåtriktad gravitation.
Vi har alla sett att ljuset bryts vid en vattenyta eller vid en glasyta i t ex
en lins.Detta kan förklaras med att ljushastigheten är lägre i vatten och glas
än den är i luft.Det förefaller alltså som om ljushastigheten c är lägre i
områden med större antal ettor.Om vi använder bilden av en eter som strömmar i
tidsled i en fyrdimensionell rymd skulle detta innebära att etern släpar efter
i områden med förhållandevis många ettor.En stor massa innebär alltså en
etereftersläpning som medför att runt massan kröks eterns strömningsriktning
inåt mot massan.Eterns strömningsriktning får alltså här en komposant i
rumsriktning.En partikel som svävar fritt i etern kommer alltså att dras in
mot massan.
Michelson-Morleys spegelförsök visade att jorden inte rör sig i förhållande
till en omgivande eter.
Eftersom föremål kan röra sig i förhållande till varandra ansåg man att de
inte alla kunde vara i vila i förhållande till omgivande eter.Man tolkade
därför försöket som att det inte kan finnas någon eter.
I ett medium som i det närmaste är inkompressibelt,som vatten,gäller att mediets
strömningsriktning blir praktiskt taget densamma i närliggande punkter.Men redan
med den kompressibilitet som luft har kan man ha närliggande vindbyar med
olika riktning.
Ombord på en ballong blåser det aldrig trots att man kan ha betydande hastighet
i förhållande till andra ballonger inom synhåll.Luftens kompressibilitet gör att
ballonger som alla befinner sig i vila i förhållande till omgivande luft ändå
kan röra sig i förhållande till varandra.
Och varför skulle etern vara inkompressibel?
Är inte föreställningen att jorden faktiskt befinner sig i vila i förhållande till
omgivande eter på samma sätt som en ballong är i vila i förhållande till omgivande
luft en mer näraliggande tolkning av Michelson-Morleys spegelförsök?
Runt massor får vi alltså en "etervind" in mot dem.Om man befinner sig tillräckligt
nära en tillräckligt stor massa kommer denna etervind att dominera över den
utåtriktade gravitationen och vi får en inåtriktad gravitation.
Gravitation är alltså utåtriktad men lokalt kring en massa inåtriktad.
Liv
===
Till en dator skaffar vi ett antal program som,med hjälp av datorns operativsystem,
åstadkommer spektakulära effekter.Till världsdatorn har bl a uppstått ett program
som vi kallar "Liv".
Liksom vi till datorn använder disketter och CD-rom för att lagra program använder
liv DNA för lagring av programet.
Vi har nyligen upptäckt hur denna lagring går till och vi är nu i full gång med
att skapa en debugger som fått namnet HUGO.
Med HUGO öppnar vi programet liv för läsning i assemblerspråk.Vi får allt i form
av anrop till världens BIOS men fortfarande har vi långt kvar innan vi kan tolka
vad vi får fram.Alla som försökt dekompilera ett program vet hur svårt det är att
hålla reda på vad instruktionerna innebär.Eftersom en dator blandar instruktioner
och data i samma minne brukar man snart blanda ihop data med instruktioner
och gå vilse i programet.Och när det gäller världens BIOS vet vi inte ens hur
data och instruktioner hålls isär.Och redan nu visar HUGO en mängd programtext
som vi inte vet om den har någon funktion.Är det bara rester av gammal fel-
programering?Är det element som haft en funktion men som senare ersatts av andra
element?Eller är det livsviktiga instruktioner?
Olika energiformer
==================
Enhetshändelser inträffar ständigt men med våra trubbiga sinnen och instrument kan
vi inte utnyttja enstaka enhetshändelser.Vi är hänvisade till att arbeta med
händelsekedjor som ger så stora förändringar att vi kan uppfatta dem.I stället
för att arbeta med enstaka enhetsceller och enhetshändelser arbetar vi med
medelvärde,varians och rumshastighet.
Våra sinnen är programerade för att anropa världens BIOS via några olika typer
av anrop och vi tolkar detta som att vi har tillgång till olika energiformer.
Men även om vi upplever att det är skillnad mellan t ex elektrisk energi och
värme behandlar vi alla energiformer enligt samma regler.
Oavsett vilken energiform det är fråga om betraktar vi energi som en produkt
av en mängd (extensiv faktor) och en intensitet (intensiv faktor).
Mängden kan bero på hur vi avgränsar det system vi betraktar.Om vi har en hink
med varmt vatten så har vi värme i den.Om vi häller upp halva hinken i en skål
får vi halva värmeenergin i skålen men det betyder inte att värme omvandlats
till någon annan energiform bara att vi avgränsat mängden på ett nytt sätt.
Om däremot den intensiva faktorn ändras kan,men behöver inte,energi omvandlas
till annan energiform.Om vi låter vattnet i hinken driva en värmemaskin omvandlas
en del värme till arbete och intensiteten,d v s temperaturen hos vattnet,sjunker.
Om den intensiva faktorn ändras från T1 till T2 kan alltså energi
omvandlas till annan energiform t ex till utvinnbart arbete.Det arbete som går att
få ut från en sådan omvandling för mängden S är
W = S (T1 - T2)
Läran om energiomvandling har utvecklats vid olika tidpunkt för olika energiformer.
Resultatet har blivit att man valt begrepp,sorter och mätmetoder på något olika
sätt så att det inte alltid är uppenbart att det grundläggandet resonemanget är
identiskt.Det krävs alltså lite tankearbete för att se vad som motsvarar vad men
det lönar sig att inse att t ex elektrisk intensitet är arbete per laddningsenhet
(V = J/As),potentiell intensitet är arbete per tyngdenhet (höjd i m är J/tyngd i N),
värmeintensitet (=temperatur) är arbete per entropienhet (K = J/(J/K)),intensitet för
pneumatisk energi (=volym) är arbete per tryckenhet (m3 = J/Pa),intensitet för
rörelseenergi (=hastighet) är arbete per rörelsemängd (=impuls) o s v.
Genom att på detta sätt se hur man organiserat tänkandet slipper man läsa statik,
dynamik,ellära,värmelära,pneumatik,fysikalisk kemi mm som av varandra oberoende
läror.Man kan identifiera det som är gemensamt och bara slå i sig det lilla som
blir kvar som unikt för varje energiform t ex vad begreppen har för namn.
Mängdändring
============
Man kan,som sagt,inte omvandla energi bara genom att ändra gränserna för den
energimängd man betraktar.Men det förekommer att mängd faktiskt skapas eller
förintas vilket medför energiomvandling.
Uppdelningen i extensiv mängdfaktor som inte ger energiomvandling vid förändring
och intensiv faktor som är lika för alla delar av mängden och som ger energi-
omvandling vid förändring är alltså inte så självklar som det kan förefalla vid
första påseendet.
För pneumatisk energi är tryck extensiv och volym intensiv faktor.Man kan se det
som att trycket åstadkoms genom att man tillför luftmängd och varje delmängd som
man tillför fyller ut hela volymen så att alla delmängderna har samma volym d v s
samma intensitet.Men det känns ändå lite besynnerligt att inte betrakta volym som
en mängdstorhet.Och om man minskar volymen på en sluten behållare så ökar trycket,
extensiv och intensiv faktor är då kopplade till varandra så att båda ändras.
Hur hanterar man fall där mängden inte är konstant?
Betrakta en vattenfylld bassäng med vertikala väggar.Den energi som vi kan ta ut
om vi tömmer bassängen är vattnets tyngd gånger dess fallhöjd.
Om vattenytan är A och bassängens höjd h blir vattnets tyngd
Fig 4
Sannolikheten att avståndet ökar är alltså större än sannolikheten att det
minskar.Partiklarna kommer alltså att uppföra sig som om de stötte bort varandra.
Vi kan uppfatta detta som en utåtriktad gravitation.
Vi har alla sett att ljuset bryts vid en vattenyta eller vid en glasyta i t ex
en lins.Detta kan förklaras med att ljushastigheten är lägre i vatten och glas
än den är i luft.Det förefaller alltså som om ljushastigheten c är lägre i
områden med större antal ettor.Om vi använder bilden av en eter som strömmar i
tidsled i en fyrdimensionell rymd skulle detta innebära att etern släpar efter
i områden med förhållandevis många ettor.En stor massa innebär alltså en
etereftersläpning som medför att runt massan kröks eterns strömningsriktning
inåt mot massan.Eterns strömningsriktning får alltså här en komposant i
rumsriktning.En partikel som svävar fritt i etern kommer alltså att dras in
mot massan.
Michelson-Morleys spegelförsök visade att jorden inte rör sig i förhållande
till en omgivande eter.
Eftersom föremål kan röra sig i förhållande till varandra ansåg man att de
inte alla kunde vara i vila i förhållande till omgivande eter.Man tolkade
därför försöket som att det inte kan finnas någon eter.
I ett medium som i det närmaste är inkompressibelt,som vatten,gäller att mediets
strömningsriktning blir praktiskt taget densamma i närliggande punkter.Men redan
med den kompressibilitet som luft har kan man ha närliggande vindbyar med
olika riktning.
Ombord på en ballong blåser det aldrig trots att man kan ha betydande hastighet
i förhållande till andra ballonger inom synhåll.Luftens kompressibilitet gör att
ballonger som alla befinner sig i vila i förhållande till omgivande luft ändå
kan röra sig i förhållande till varandra.
Och varför skulle etern vara inkompressibel?
Är inte föreställningen att jorden faktiskt befinner sig i vila i förhållande till
omgivande eter på samma sätt som en ballong är i vila i förhållande till omgivande
luft en mer näraliggande tolkning av Michelson-Morleys spegelförsök?
Runt massor får vi alltså en "etervind" in mot dem.Om man befinner sig tillräckligt
nära en tillräckligt stor massa kommer denna etervind att dominera över den
utåtriktade gravitationen och vi får en inåtriktad gravitation.
Gravitation är alltså utåtriktad men lokalt kring en massa inåtriktad.
Liv
===
Till en dator skaffar vi ett antal program som,med hjälp av datorns operativsystem,
åstadkommer spektakulära effekter.Till världsdatorn har bl a uppstått ett program
som vi kallar "Liv".
Liksom vi till datorn använder disketter och CD-rom för att lagra program använder
liv DNA för lagring av programet.
Vi har nyligen upptäckt hur denna lagring går till och vi är nu i full gång med
att skapa en debugger som fått namnet HUGO.
Med HUGO öppnar vi programet liv för läsning i assemblerspråk.Vi får allt i form
av anrop till världens BIOS men fortfarande har vi långt kvar innan vi kan tolka
vad vi får fram.Alla som försökt dekompilera ett program vet hur svårt det är att
hålla reda på vad instruktionerna innebär.Eftersom en dator blandar instruktioner
och data i samma minne brukar man snart blanda ihop data med instruktioner
och gå vilse i programet.Och när det gäller världens BIOS vet vi inte ens hur
data och instruktioner hålls isär.Och redan nu visar HUGO en mängd programtext
som vi inte vet om den har någon funktion.Är det bara rester av gammal fel-
programering?Är det element som haft en funktion men som senare ersatts av andra
element?Eller är det livsviktiga instruktioner?
Olika energiformer
==================
Enhetshändelser inträffar ständigt men med våra trubbiga sinnen och instrument kan
vi inte utnyttja enstaka enhetshändelser.Vi är hänvisade till att arbeta med
händelsekedjor som ger så stora förändringar att vi kan uppfatta dem.I stället
för att arbeta med enstaka enhetsceller och enhetshändelser arbetar vi med
medelvärde,varians och rumshastighet.
Våra sinnen är programerade för att anropa världens BIOS via några olika typer
av anrop och vi tolkar detta som att vi har tillgång till olika energiformer.
Men även om vi upplever att det är skillnad mellan t ex elektrisk energi och
värme behandlar vi alla energiformer enligt samma regler.
Oavsett vilken energiform det är fråga om betraktar vi energi som en produkt
av en mängd (extensiv faktor) och en intensitet (intensiv faktor).
Mängden kan bero på hur vi avgränsar det system vi betraktar.Om vi har en hink
med varmt vatten så har vi värme i den.Om vi häller upp halva hinken i en skål
får vi halva värmeenergin i skålen men det betyder inte att värme omvandlats
till någon annan energiform bara att vi avgränsat mängden på ett nytt sätt.
Om däremot den intensiva faktorn ändras kan,men behöver inte,energi omvandlas
till annan energiform.Om vi låter vattnet i hinken driva en värmemaskin omvandlas
en del värme till arbete och intensiteten,d v s temperaturen hos vattnet,sjunker.
Om den intensiva faktorn ändras från T1 till T2 kan alltså energi
omvandlas till annan energiform t ex till utvinnbart arbete.Det arbete som går att
få ut från en sådan omvandling för mängden S är
W = S (T1 - T2)
Läran om energiomvandling har utvecklats vid olika tidpunkt för olika energiformer.
Resultatet har blivit att man valt begrepp,sorter och mätmetoder på något olika
sätt så att det inte alltid är uppenbart att det grundläggandet resonemanget är
identiskt.Det krävs alltså lite tankearbete för att se vad som motsvarar vad men
det lönar sig att inse att t ex elektrisk intensitet är arbete per laddningsenhet
(V = J/As),potentiell intensitet är arbete per tyngdenhet (höjd i m är J/tyngd i N),
värmeintensitet (=temperatur) är arbete per entropienhet (K = J/(J/K)),intensitet för
pneumatisk energi (=volym) är arbete per tryckenhet (m3 = J/Pa),intensitet för
rörelseenergi (=hastighet) är arbete per rörelsemängd (=impuls) o s v.
Genom att på detta sätt se hur man organiserat tänkandet slipper man läsa statik,
dynamik,ellära,värmelära,pneumatik,fysikalisk kemi mm som av varandra oberoende
läror.Man kan identifiera det som är gemensamt och bara slå i sig det lilla som
blir kvar som unikt för varje energiform t ex vad begreppen har för namn.
Mängdändring
============
Man kan,som sagt,inte omvandla energi bara genom att ändra gränserna för den
energimängd man betraktar.Men det förekommer att mängd faktiskt skapas eller
förintas vilket medför energiomvandling.
Uppdelningen i extensiv mängdfaktor som inte ger energiomvandling vid förändring
och intensiv faktor som är lika för alla delar av mängden och som ger energi-
omvandling vid förändring är alltså inte så självklar som det kan förefalla vid
första påseendet.
För pneumatisk energi är tryck extensiv och volym intensiv faktor.Man kan se det
som att trycket åstadkoms genom att man tillför luftmängd och varje delmängd som
man tillför fyller ut hela volymen så att alla delmängderna har samma volym d v s
samma intensitet.Men det känns ändå lite besynnerligt att inte betrakta volym som
en mängdstorhet.Och om man minskar volymen på en sluten behållare så ökar trycket,
extensiv och intensiv faktor är då kopplade till varandra så att båda ändras.
Hur hanterar man fall där mängden inte är konstant?
Betrakta en vattenfylld bassäng med vertikala väggar.Den energi som vi kan ta ut
om vi tömmer bassängen är vattnets tyngd gånger dess fallhöjd.
Om vattenytan är A och bassängens höjd h blir vattnets tyngd
 På liknande sätt gäller för rörelseenergi att rörelsemängden d v s impulsen mv
varierar med intesiteten d v s med hastigheten v.Och även här får vi ett liknande
uttryck för uttagbar energi.Den blir
W = m v2/2
Transformatorn och väduren
========================
Om man har energimängden E = S1 T1 kan man omvandla denna till den
lika stora energimängden E = S2 T2 . Man kan alltså ändra intensitet och
mängd så länge deras produkt förblir oförändrad. En stor tyngd med liten
höjd kan alltså omvandlas till en liten tyngd med stor höjd. En stor laddning
med liten spänning kan ge en liten laddning med hög spänning. Men hur gör
man för att åstadkomma en sådan omvandling?
Ett vanligt sätt är att omvandla till annan energiform och därefter återgå till
den ursprungliga energiformen. Om man har lägesenergi kan man omvandla
den till rörelseenergi som man omvandlar till lägesenergi.
Om en kula med tyngden m1g ligger på ett bord med höjden h1 har man
lägesenergin E = m1g h1. Om kulan rullar över bordskanten omvandlas
denna lägesenergi till rörelseenergi. På golvet kan man så lägga en
gungbräda med en kula med tyngden m2g på den sida som inte träffas av
den fallande kulan. Arrangerar man det hela på rätt sätt kan resultatet
bli att hela rörelseenergin (som är lika med den ursprungliga lägesenergin)
överförs till den andra kulan som kastas upp till höjden h2 så att
E = m1g h1 = m2g h2
Anordningen är alltså en transformator som transformerar kulhöjden h1 till
kulhöjden h2.
Inom elöverföring använder man ofta transformatorer för att omvandla
spänning mellan de krav som ställs för överföringen och de krav som ställs
för användningen. Den energi som tillförs transformatorns primärlindning
omvandlas till magnetisk energi i transformatorkärnan och den magnetiska
energin omvandlas till elektrisk energi i primär och sekundärlindningen. Det
man inte tar ut via sekundärlindningen återmatas via primärlindningen
tillbaka till energikällan.
Antag att jag bor vid en strand. Huset ligger på höjden h2 över sjöytan.
På vägen upp till huset finns en källa som ligger på höjden h1 över
sjöytan så att h1 är mindre än h2. Hur skall jag göra för att
få vatten från källan upp till huset?
Jag kan använda en hydraulisk vädur eller med ett annat ord en stöthävert.
Från källan drar jag ett rör ner i sjön. I neränden på detta sätter jag en
förgrening där ett rör går upp till huset. I röret upp till huset sätter jag en
backventil och nedanför grenen sätter jag en styrd ventil. Jag fyller systemet
med vatten och öppnar den styrda ventilen. Vatten strömmar då från källan
till sjön. När vattnet fått ordentlig fart stänger jag den styrda ventilen.
För att bromsa ett yxhugg på bromssträckan noll krävs oändlig kraft. På
samma sätt krävs oändligt mottryck för att på bromssträckan noll stoppa ett
vatttenflöde i ett slutet rör. När jag stänger den styrda ventilen får jag
alltså ett stagnationstryck som blir oändligt om det inte finns någon möjlighet
för vattnet att bromsa in genom att något sviktar eller genom att det finns
någon annan väg för vattnet att strömma. Här finns en annan väg. Det är
röret upp till huset. När jag stänger den styrda ventilen stiger alltså trycket
tills det överstiger trycket i röret upp till huset. Då öppnar backventilen och
vatten strömmar upp till huset.
Källvattnets lägesenergi omvandlas till rörelseenergi när vatten strömmar
från källan till sjön. När jag stänger den styrda ventilen omvandlas rörelse-
energin till lägesenergi när vatten trycks upp till huset.
Den elektriska motsvarigheten till en vattenmassa som strömmar i ett rör är
en elektrisk ström genom en induktans. Om man plötsligt bryter strömmen
får man en spänning som motsvarar ett stagnationstryck. Spänningen blir
U = L di/dτ
På samma sätt som man kan använda en hydraulisk vädur för att pumpa
vatten från en låg till en hög nivå kan man göra en "elektrisk vädur" som
pumpar elektrisk laddning från en låg spänning till en hög spänning.
På liknande sätt gäller för rörelseenergi att rörelsemängden d v s impulsen mv
varierar med intesiteten d v s med hastigheten v.Och även här får vi ett liknande
uttryck för uttagbar energi.Den blir
W = m v2/2
Transformatorn och väduren
========================
Om man har energimängden E = S1 T1 kan man omvandla denna till den
lika stora energimängden E = S2 T2 . Man kan alltså ändra intensitet och
mängd så länge deras produkt förblir oförändrad. En stor tyngd med liten
höjd kan alltså omvandlas till en liten tyngd med stor höjd. En stor laddning
med liten spänning kan ge en liten laddning med hög spänning. Men hur gör
man för att åstadkomma en sådan omvandling?
Ett vanligt sätt är att omvandla till annan energiform och därefter återgå till
den ursprungliga energiformen. Om man har lägesenergi kan man omvandla
den till rörelseenergi som man omvandlar till lägesenergi.
Om en kula med tyngden m1g ligger på ett bord med höjden h1 har man
lägesenergin E = m1g h1. Om kulan rullar över bordskanten omvandlas
denna lägesenergi till rörelseenergi. På golvet kan man så lägga en
gungbräda med en kula med tyngden m2g på den sida som inte träffas av
den fallande kulan. Arrangerar man det hela på rätt sätt kan resultatet
bli att hela rörelseenergin (som är lika med den ursprungliga lägesenergin)
överförs till den andra kulan som kastas upp till höjden h2 så att
E = m1g h1 = m2g h2
Anordningen är alltså en transformator som transformerar kulhöjden h1 till
kulhöjden h2.
Inom elöverföring använder man ofta transformatorer för att omvandla
spänning mellan de krav som ställs för överföringen och de krav som ställs
för användningen. Den energi som tillförs transformatorns primärlindning
omvandlas till magnetisk energi i transformatorkärnan och den magnetiska
energin omvandlas till elektrisk energi i primär och sekundärlindningen. Det
man inte tar ut via sekundärlindningen återmatas via primärlindningen
tillbaka till energikällan.
Antag att jag bor vid en strand. Huset ligger på höjden h2 över sjöytan.
På vägen upp till huset finns en källa som ligger på höjden h1 över
sjöytan så att h1 är mindre än h2. Hur skall jag göra för att
få vatten från källan upp till huset?
Jag kan använda en hydraulisk vädur eller med ett annat ord en stöthävert.
Från källan drar jag ett rör ner i sjön. I neränden på detta sätter jag en
förgrening där ett rör går upp till huset. I röret upp till huset sätter jag en
backventil och nedanför grenen sätter jag en styrd ventil. Jag fyller systemet
med vatten och öppnar den styrda ventilen. Vatten strömmar då från källan
till sjön. När vattnet fått ordentlig fart stänger jag den styrda ventilen.
För att bromsa ett yxhugg på bromssträckan noll krävs oändlig kraft. På
samma sätt krävs oändligt mottryck för att på bromssträckan noll stoppa ett
vatttenflöde i ett slutet rör. När jag stänger den styrda ventilen får jag
alltså ett stagnationstryck som blir oändligt om det inte finns någon möjlighet
för vattnet att bromsa in genom att något sviktar eller genom att det finns
någon annan väg för vattnet att strömma. Här finns en annan väg. Det är
röret upp till huset. När jag stänger den styrda ventilen stiger alltså trycket
tills det överstiger trycket i röret upp till huset. Då öppnar backventilen och
vatten strömmar upp till huset.
Källvattnets lägesenergi omvandlas till rörelseenergi när vatten strömmar
från källan till sjön. När jag stänger den styrda ventilen omvandlas rörelse-
energin till lägesenergi när vatten trycks upp till huset.
Den elektriska motsvarigheten till en vattenmassa som strömmar i ett rör är
en elektrisk ström genom en induktans. Om man plötsligt bryter strömmen
får man en spänning som motsvarar ett stagnationstryck. Spänningen blir
U = L di/dτ
På samma sätt som man kan använda en hydraulisk vädur för att pumpa
vatten från en låg till en hög nivå kan man göra en "elektrisk vädur" som
pumpar elektrisk laddning från en låg spänning till en hög spänning.
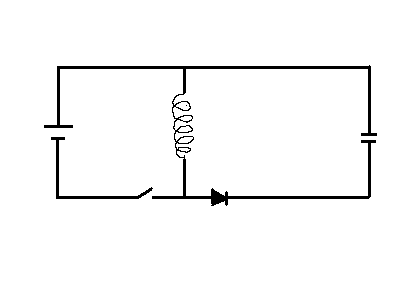 Fig 5
Den viktiga skillnaden mellan en transformator och en elektrisk vädur är att
transformatorn transformrar en växelspänning U1 till en annan spänning U2
där förhållandet mellan dessa båda spänningar bestäms av förhållandet
mellan antalet lindningsvarv i primärlindning och antalet lindningsvarv i
sekundärlindning. Stöthäverten, d v s väduren, däremot överför laddning från
matningsspänningen U1 till utspänningen U2 oberoende av vilket värde U2 har.
Om sorter
=========
Påståendet att 15 äpplen är 1 glas mjölk och 3 ostbitar är uppenbart nonsens.
Man kan inte lägga ihop mjölk och ost och än mindre få äpplen som resultat.
I exemplet ovan kan vi kalla 15 , 1 och 3 för mätetal och "äpplen" , "glas
mjölk" och "ostbitar" för sorter.Vanligtvis behöver vi hantera storheter av
varje sort för sig.Vi kan t ex säga att 10 äpplen plus 5 äpplen är 15 äpplen.
Alla termer skall alltså ha samma sort.
När man börjar läsa fysik är denna regel ett mycket användbart hjälpmedel för
att kontrollera beräkningar.När man ställer upp olika samband lär man sig att
alltid göra en sortkontroll d v s att se efter vilken sort de ingående termerna
har.Skulle någon term ha en annan sort än de övriga tyder det på att man gjort
något fel.Om man försöker lägga ihop längd mätt i meter med tid mätt i sekunder
har man troligen gjort något fel.
Våra måttsystem har utvecklats ur ungefärliga begrepp som volymen "tunna råg",
tiden "en halvdag",temperaturen "byxljummen" o s v.Men ökad köpenskap och ökad
rörlighet ställde krav på exaktare mätningar.Handlaren som köpte råg i tunnor
och sålde i påsar behövde veta hur många påsar det gick på en tunna.Och den
som skulle köra och hämta någon från tåget behövde veta när tåget skulle
komma.
Man började fundera på hur och vad vi kunde mäta.Till en början var det t ex
inte alls självklart att en fast mängd kunde mätas upp med samma typ av
volymmätning som användes för vätskor.Gjorde man en flätad måttkorg för att
mäta upp råg kunde den inte användas för vatten.Och om man sög upp vatten i
en mätkammare kunde man inte använda samma utrustning för att mäta upp råg.
Men så småningom enades vi om att sådana problem är av praktisk natur och
att de inte motsäger det principiella påståendet att det går att åstadkomma
volymmått som är användbara för såväl råg som vatten.Vi kunde göra oss av
med ett antal gamla mått och i stället mäta alla volymer i samma mått.
Så började man fundera på hur många olika sorter man behövde utgå ifrån för
att få fram alla sorter som man behövde i det dagliga livet.Om man hade bestämt
sig för en längd som fick utgöra längdenhet kunde man göra en kvadrat med denna
längdenhet som sida.Därigenom fick man en ytenhet utan att man behövde bestämma
sig för någon ny grundstorhet.Och man kunde åstadkomma en volymenhet genom att
göra en kub med längdenheten som sida.
Man kom till att man behövde enheter för längd,massa och tid för att kunna
härleda praktiskt taget alla de sorter man behövde.Vi fick cgs-systemet med
centimeter för längd,gram för massa och sekund för tid.
Om man skall kasta en sten gäller att kraften som man kastar med blir massan
gånger accelerationen.Hastighet är förflyttning per sekund och har alltså sorten
cm/s.Accelerationen är hastighetsändring per sekund och får alltså sorten cm/s2.
Massan mäts i gram och sorten för kraft blir alltså g cm/s2.Denna sort kan man
använda för alla krafter oavsett om de sätter fart på en kaststen eller lyfter
mjölsäckar.
En nackdel med cgs-systemet var att det inte gav en enhetlig behandling av
elektriska storheter.Man kunde dels utgå från elektrostatisk kraftverkan mellan
laddade partiklar dels från magnetisk kraftverkan mellan elektriskt laddade
partiklar i rörelse.Resultatet blev två måttsystem ese (elektrostatiska enheter)
och eme (elektromagnetiska enheter).Dessutom fick man ofta räkna med obekvämt
många nollor för storheter av alldaglig storhet.
Resultatet blev att man övergick till MKSA-systemet baserat på meter,kilogram,
sekund och ampere.Genom att lägga till ampere fick man en enhetlig behandling
av elektriska storheter.
Under en tid användes även det s k tekniska systemet som inte hade massa utan
kraft som en grundenhet.I stället för kilogram använde man tyngden av ett
kilogram som grundenhet.Men resultatet blev att många fick svårt att skilja
mellan massa och kraft.Fortfarande ser man manometrar graderade i kg/cm2 när
man naturligtvis menar kp/cm2 där kp (kilopond) är tyngden (=den kraft
som jordens dragningskraft ger) av ett kg.
Efter vissa justeringar blev MKSA-systemet internationell standard och döptes
om till SI-systemet.
Multiplicera en tid som har sorten s med en hastighet som har sorten m/s så får
resultatet sorten s m/s. Förkorta med s så ser man att resultatet får sorten m
vilket innebär att det är en längd.Tid gånger hastighet ger alltså längd.Vet man
hur lång tid en bil kör och med vilken hastighet den går kan man alltså räkna ut
hur långt den kommer.
Multiplicerar man en tid (s) med en kraft (kg m/s2) och dividerar med en massa
(kg) får resultatet sorten m/s.Resultatet blir alltså en hastighet.Om man vet hur
stor massa den sten man kastar har,hur lång tid kastet tar och vilken kraft man
kastar med kan man alltså räkna ut stenens utgångshastighet.
Ett sätt att lösa gymnasietidens övningsuppgifter och skrivningar var,åtminstone på
min gymnasietid,att se efter
Vilka storheter är givna och vad har de för sorter
Vilka storheter efterfrågas och vad har de för sorter
Hur kan man kombinera givna storheter så att resultatet får efterfrågad sort
Det är naturligtvis inte alltid självklart vilken hastighet som hör ihop med vilken
tid och vilken massa som påverkas av vilken kraft men metoden brukade räcka för att
ge godkänt även om man inte hade någon aning om vad man gjorde.
Metoden gav god utdelning för minimalt arbete och efteråt har jag förstått att jag
faktiskt lärde mig mer än de som mödosamt pluggade in alla formler och regler.
Måttsystem
==========
Om man vill mäta längden på en sträcka kan man lägga ena tummen vid ändpunkten.Så
lägger man den andra tummen intill,"vandrar" med tummarna bort till andra ändpunkten
och räknar antalet tumbredder.Är det fråga om en lite längre sträcka kan man sätta
hälen vid ena ändpunkten,"vandra" tå mot häl till andra ändpunkten och räkna antalet
fotlängder.
Detta är ett praktiskt sätt som vi nog har medfött.Och för sortomvandlingen mellan
tum och fot använde man sig av att det går 12 tum på en fot.Tolv är ett utmärkt
sortomvandlingstal som är jämnt delbart med 2,3,4 och 6.
För volym och vikt utgick man från vad man kunde lyfta,hur mycket man kunde dricka
o dyl.Tid angav man ofta i den tid som åtgick för någon vardaglig händelse o s v.
Detta var praktiskt men inexakt.Människor hade olika breda tummar och olika långa
fötter.Med franska revolutionen kom en ny syn på mått och vikt.Man släppte kravet
på anknytning till dagligt bruk och satte sig vid skrivbordet för att konstruera
"rationella" mått.
Vid skrivbordet föreföll tio vara bättre än tolv för omräkning mellan olika mått
av samma slag.Man skapade därför ett system med tiopotens-multiplar för att
åstadkomma hanterliga mått.Vårt talsystem har tio som bas därför att vi räknat
på våra tio fingrar (utom danskarna som även räknat på tårna).Men tio är bara
jämnt delbart med 2 och 5 vilket bl a ger problem med den,i praktiken ofta
förekommande,divisionen med 3.
Så skulle man överge tum som längdmått och i stället välja en längdenhet som alla
hade tillgång till och som var exakt lika lång för alla.Vid skrivbordet kan man
se jorden som tillgänglig för alla.Man utgick därför från jordens omkrets.Men det
blev en så opraktiskt stor enhet att man t o m vid skrivbordet insåg att man
måste välja en mindre del.Man delade därför in omkretsen i fyra kvadranter och
definierade längdenheten meter som en tiomiljontedel av en sådan kvadrant d v s
som en fyrtiomiljontedel av jordens omkrets.
Det låg också något av en tanke i att använda jordrotationen för att definiera en
tidsenhet d v s att låta sekund vara en viss del av dygnet och att använda jordens
omkrets för att fastställa en längdenhet.På det viset knöt man både längd och
tid till jordklotet.
Nu hade man fått en exakt och för alla lika längdenhet.Nu var det bara att sätta
igång och tillverka meterstavar för praktiska mätningar.Man skickade ut lantmätare
för att mäta upp jordens omkrets och fastställa meterns längd.De mätte men
det där med exakthet var inte så enkelt i verkligheten.När man hade prånglat ut
alltför många meterstavar för att kunna ta tillbaks dem började man förstå att
mätningarna var så felgjorda att man inte kunde behålla den ursprungliga
definitionen.
Det stolta meterprojektet,skrivbordsförnuftets triumf över vardagen,flaggskeppet i
krämarnas uppror mot adeln,hade havererat.
Nu gällde det att rädda ansiktet.Man gjorde en arkivmeter (antagligen tog man
helt enkelt någon prototyp till meterstav) som stämde väl med de meterstavar
man prånglat ut och förkunnade att en meter var arkivmeterns längd.Och man
vände sig till Napoleon.Han förfogade över argument av annat slag och kunde
sprida metersystemet utan några besvärande frågor om varför arkivmetern hade
just den längden.England och USA,som inte kom under Napoleons välde,behöll
tumsystemet långt in på 1900-talet.
Som enhet för massa tänkte man sig att använda gram definierat som massan hos
en kubikcentimeter vatten.Men även här övergick man till att knyta definitionen
till en arkivenhet.
Det här med arkivmeter och arkivkilogram fungerade hjälpligt men det smakade lite
nederlag om det.Krämarna hade inte lyckats lyfta sig över sin praktiska användning
av mätstickor och vikter för att skapa ett måttsystem som förankrats i något högre
än vardagens triviala utminutering av handelsbodens produkter.
Men om vi kunde finna någon universell,överallt och för alla lika hastighet skulle
vi kunna koppla längd och tid till varandra.Vi skulle kunna multiplicera tidsenheten
med denna hastighet och få en längd som vi kunde använda för att definiera en
längdenhet.
Ljushastigheten är en sådan universell hastighet och idag knyter vi tidsenheten till
periodtiden och längdenheten till våglängden för en viss spektrallinje.
På liknande sätt kan vi, med hjälp av Plancks konstant, knyta enheten för massa
till enheterna för längd och tid.
Och som framgår ovan är det möjligt att definiera en absolut tid i en,av våra
måttsystem oberoende,absolut enhet.För närvarande är våra möjligheter att mäta
denna enhet så dåliga att vi inte utnyttjar denna möjlighet.Vi vill inte göra
om fadäsen med mätningen av jordens omkrets.Men vi vet idag att det är möjligt
att skapa ett måttsystem som är helt fritt från godtyckliga arkivmått.
DEL 4
Etervinden
==========
Världen innehåller något. Detta "något" kan vi naturligtvis ge ett namn. Vi kan
kalla det gud, alluppfyllande Brahma, världseter eller något annat.
Låt oss döpa innehållet i världen till "Eter".
När vi bestämt oss för namnet är det dags att fastställa eterns egenskaper, att
finna egenskaper som liknar sådant som vi känner igen från den bild av världen
som våra sinnen ger oss.
I en värld med absolut jämnt fördelad eter kan inga punkter urskiljas i
rummet och inga händelser kan inträffa och ordnas i tid. Rum och tid
saknar mening i en sådan värld. Etern måste alltså ha egenskapen att den
kan störas så att den avviker från omgivningen. Det är sådana störningar
som ger begreppen "rum" och "tid" innebörd.
Om vi projicerar vår värld på ett koordinatsystem med tre rumsaxlar och
en koordinattidsaxel får vi en bild som är fullständig i den meningen att
två eterstörningar alltid växelverkar om de har samtliga koordinater lika
med varandra.
I en värld som står stilla, d v s som rör sig på samma sätt som observatören
växer koordinattiden i samma takt som parametertiden. Etern flödar alltså i
koordinattidsriktningen. Vår värld är alltså en etervind som (huvudsakligen)
blåser i koordinattidsriktningen.
Etervind kan beskrivas som en fyrdimensionell vektor c. Vi kan alltså se
världen som ett vektorfält där varje punkt tilldelas en fyrdimensionell
vektor som anger etervinden i punkten.
Vi har svårt att tänka i fyra dimensioner och projicerar därför ofta den
fyrdimensionella världsbilden på en tredimensionell bild med enbart
rumskoordinater. Vi uppfattar alltså en tredimensionell bild av en
fyrdimensionell etervind. Det vi uppfattar i denna är störningar som
svävar i vinden som ballonger eller moln i luft.
I den fyrdimensionella rymden kan vi lägga in ett cartesianskt koordinatsystem
med axlarna x , y , z och t. I det tredimensionella rummet kan vi lägga in
ett cartesianskt koordinatsystem med axlarna x , y och z. För att skilja
mellan den fyrdimensionella vektorn c och dess tredimensionella projektion
kan vi använda beteckningarna c4 och c3.
Så här kan vi naturligtvis göra men för att det skall vara någon mening med
det måste c4 och/eller c3 ha någon egenskap som är bekväm att
hantera. En sådan skulle kunna vara att det fyrdimensionella vektorfältet är
källfritt d v s att
div c4 = 0
En annan tänkbar egenskap skulle kunna vara att en störning av etern innebär
att
div c3 ≠ 0
Låt oss anta att det är så.
En eterstörning kallas "partikel".
För en vanlig partikel är div c3 < 0. En sådan partikel är alltså en sänka
för etervinden. Den är en uppvind i koordinattidsled som medför att etervinden
runt om den viker av in mot partikelcentrum. Denna inströmning mot centrum
kallas för gravitation.
Beloppet av c4 kallas för ljushastighet. Den ostörda etern strömmar alltså
med ljushastighet i koordinattidsled. Vid en partikel avlänkas strömnings-
riktningen så att vi får en hastighetskomposant i rumsled samtidigt som
hastigheten i koordinattidsled minskar.
Om inströmningen mot partikelcentrum sker i form av en virvel blir
rot c4 ≠ 0. I vanliga fall blir rot c4 en vektor i koordinat-
tidsriktning, d v s inströmningen sker i en virvel kring koordinattids-
axeln. Detta kallas elektrisk laddning.
Ballonger och moln som flyter omkring i atmosfären rör sig slumpmässigt
i förhållande till varandra. Men inte bara slumpmässigt. Luftrörelser
har en tendens att samordna sig till vindilar. På liknande sätt gäller att
partiklar som svävar i etern inte bara rör sig slumpmässigt i förhållande
till varandra. De har en tendens att ordna sig i mönster, ofta i mönster
som upprepas likt tapetmönster eller fjädermoln.
Små partiklar slår sig samman till större t ex till elektroner eller till
ännu störe som protoner och neutroner. Dessa slår sig i sin tur samman till
atomer som slår sig samman till molekyler som i sin tur bildat materia.
Sådan sammanslagning sker efter mycket säregna mönster. Uppenbarligen
följer mönsterbildningen mycket strikta och enkla regler men vi vet mycket
lite om dessa. Vi kan t ex observera att förhållandet mellan protonens
massa och elektronens massa alltid är 1800 men vi kan inte, med
utgångspunkt från andra kända egenskaper hos etern komma fram till detta
förhållande.
Bildade mönster har (ibland) en viss stabilitet. I ett stycke koppar ligger
kopparatomerna ordnade på bestämda platser som blommorna på en blommig
tapet. Detta mönster ändras inte även om vi förflyttar kopparstycket. För
att bryta mönstret får vi ta till verktyg med ännu stabilare mönster
t ex smältdegel, plåtsax eller såg.
Reglerna för mönsterbildning innefattar även regler för samband mellan
orsak och verkan.
Vi kan t ex ha ett mönster A där ett område med enbart kolatomer omges av
syremolekyler. Vi kan också ha ett mönster B där alla kolatomer ingår i
koldioxidmolekyler. Mönster A har en viss stabilitet och det kan bestå
trots att mönster B har större sannolikhet. Men om vi kan starta en
övergång från A till B i ett litet hörn av kolstycket kan vi få en spontan
fortsättning så att hela A övergår till B. Att tända på ett kolstycke i
ett hörn är alltså en orsak till en verkan som består i att hela kolstycket
brinner upp. De regler som gäller för övergång från A till B innehåller
alltså information om hur man kan orsaka d v s starta övergången.
Termodynamikens huvudsatser ger oss vissa regler för övergång mellan olika
mönster.
Vi har funnit att befintliga mönster kan ha en viss stabilitet men om
denna stabilitet bryts övergår de till mer sannolika mönster. Vår förmåga
inskränker sig till störa stabiliteten i befintliga system och därigenom
orsaka förändringar. Men med det kan vi komma långt. Om vi bara vet vad
som är ett mer sannolikt mönster kan vi arrangera förändringar så att de
motsvarar våra önskemål.
Högsta möjliga hastighet
========================
Universum är stort med många partiklar. Det gör att det blir svåröverskådligt.
Men de regler som gäller är, så vitt vi vet, samma som gäller för en liten
samling partiklar. Låt oss därför tänka oss ett litet universum med t ex
enbart 10 partiklar.
Läget för en partikel (A) i detta lilla universum bestäms av dess läge i
förhållande till de övriga 9 partiklarna. A:s läge anges alltså av 9 avstånd
till andra partiklar.
Om A ändrar läge förändras alla dess 9 avstånd. Men ändringen påverkar även
alla övriga partiklars läge eftersom 1 av deras 9 avstånd ändras.
Vi kan dela in A:s lägesförändring i steg som vart och ett omfattar minsta
detekterbar lägesförändring. Den minsta detekterbara lägesförändringen kan vi
kalla en längdenhet.
Varje gång någon partikel, t ex A, flyttas en längdenhet inträffar en
förändring som är minsta detekterbara förändring. En sådan förändring kallar
vi för händelseenhet eller enhetshändelse. Om A flyttas en längdeenhet
inträffar alltså en händelseenhet som berör A men den berör även alla andra
partiklar eftersom deras avstånd till A förändras. En händelse som berör A
innebär alltså en förändring för alla 10 partiklarna. Vi säger att tiden
går en tidsenhet för alla 10 partiklarna.
Om A flyttas 100 längdenheter och övriga partiklar ligger stilla inträffar
alltså 100 händelseenheter som innebär att tiden går 100 tidsenheter. A:s
hastighet blir då 100/100 = 1 längdenhet/tidsenhet. Detta är den teoretiskt
sett högsta hastighet som A kan ha.
Om A flyttas 100 längdenheter under det att B flyttas 200 längdenheter, C
flyttas 50 längdenheter och övriga partiklar ligger stilla inträffar
100 + 200 + 50 händelseenheter under A:s förflyttning. Tiden går alltså
350 tidsenheter och A:s hastighet blir 100/350 = 0,29 längdenheter/tidsenhet.
Om alla 10 partiklarna är lika och med samma sannolikhet för lägesförändring
kommer partikel A att, i genomsnitt, ändra läge var tionde gång. Den och alla
de andra partiklarna får då hastigheten 1/10 = 0,1 längdenheter/tidsenhet.
Alla partiklar rör sig då med hastigheten 0,1 längdenheter/tidsenhet men om
rörelseriktningen är helt slumpmässig kommer de bara att röra sig någon
längdenhet fram och tillbaka. De kommer alltså att ligga stilla om man
betraktar dem med en upplösning i längd på några tusen längdenheter. Då kommer
man enbart att se en rörelse hos de partiklar där rörelseriktningen inte
är helt slumpmässig.
Om vårt universum innehåller 10364 kvanta blir hastigheten för varje
kvanta 10-364 längdenheter/tidsenhet. Ett kvanta som ständigt rör sig
åt samma håll ser, vid låg upplösning, ut att röra sig medan de kvanta som rör
sig slumpmässigt åt olika håll ser ut att stå stilla.
Ett kvanta som rör sig med 10-364 längdenheter/tidsenhet åt samma
håll har den högsta hastighet som kan uppnås genom koncentration av rörelse-
riktning till en enda riktning. Denna hastighet kallar vi ljushastighet.
Varje kvanta marscherar alltså taktfast. Genom att gå ett steg fram och ett
tillbaka kan det göra "På stället marsch" och genom att gå två steg fram och
ett tillbaka eller genom att gå fram i zig-zag kan det gå sakta framåt. Den
högsta hastigheten når det om varje steg tas rakt fram. Den hastigheten kallas
ljushastighet.
Men om man kan få ett kvanta att inte bara gå rakt fram utan också gå i otakt
med högre takt än omgivningen skulle det kunna få ännu högre hastighet.
Detta skulle alltså innebära att det finns en möjlig hastighet som är
10364 gånger högre än ljushastigheten. Att det kan ligga något i
Science Fiction författarnas dröm att vi en gång i tiden skulle kunna komma
runt de begränsningar som ljushastigheten sätter. Att ljusvallen skulle kunna
visa sig vara som ljudvallen, ett problem som ställt en rad krav men inte ett
oöverstigligt hinder.
Vad är mönster?
===============
Vi kan se världen som en struktur av möjliga kvantapositioner. Dessa är
antingen fyllda eller tomma. Vi kan kalla detta för "realvärlden".
För att beskriva realvärlden kan vi tilldela varje kvantaposition en bit
d v s en etta för fylld position och en nolla för tom position. Vi kan
kalla denna beskrivning för "symbolvärlden".
Symbolvärlden innehåller långt fler nollor än ettor. Den innehåller alltså
stora sjok med enbart nollor. Det ligger då nära till hands att ersätta
t ex en rad med en miljon nollor med ett tecken som betyder "Här följer
en miljon nollor". Genom att använda tecken av denna typ kan vi beskriva
världen med en beskrivning som är kortare än symbolvärlden. Vi kan kalla
en sådan komprimerad beskrivning för "kodvärlden".
Symbolvärlden innehåller så mycket fler nollor än ettor att det alltid är
möjligt att åstadkomma en fullständig och felfri kodvärld med färre tecken
än symbolvärlden. Om dessutom ettorna uppträder i ordnade grupper kan
kodvärlden minskas ytterligare. Det visar sig att ettor uppträder i
grupper som vi kallar elektroner, protoner och neutroner. Genom att i
kodvärlden införa tecken för elektroner, protoner och neutroner kan vi
väsentligt minska kodvärlden. En elektron och dess läge kan i kodvärlden
beskrivas med några tusen bits vilket är långt mindre än i symbolvälden
där det ingår ungefär 10244 ettor i en elektron.
Om vi betecknar antal tecken i symbolvärlden med Sy och antalet tecken i
kodvärlden med Ko kan vi definiera världens komprimerbarhet som
Sy - Ko
Zip = --------
Sy
Zip för hela eller för en del av världen antar värden mellan 0 och 1. Att
antalet nollor i symbolvärlden är mycket större än antalet ettor innebär
Zip alltid blir större än noll. Vi kan kalla det minsta värde som Zip kan
anta vid normal fördelning mellan ettor och nollor för Zipmin.
Att världen ordnar sig till ett mönster innebär att Zip ökar. Vi kan ange
hur organiserad världen eller en del av världen är genom att definiera
mönstergraden Struct enligt
Zip - Zipmin
Struct = -------------
1 - Zipmin
Ett problem med kodvärlden är att det kan finnas sätt att kortfattat
beskriva ett mönster utan att vi känner till hur en sådan beskrivning kan
göras. Ett exempel på detta är fraktaler. En fraktal ger en bild som vi
direkt upplever som ett ordnat mönster. Den har alltså Zip mycket nära
1 och högt Struct. Men för några årtionden sedan visste vi inte att
ett sådant mönster kunde beskrivas med en mycket kort beskrivning i
kodvärlden.
Om man ser på en fraktalbild utan att veta något om fraktaler ser man
direkt att det är fråga om ett ordnat mönster som alltså måste ha en
kort beskrivning i kodvärlden även om man inte vet hur denna beskrivning
ser ut. På liknande sätt har en melodi en kortare beskrivning i
kodvärlden än en rad slumpmässiga toner även om vi inte kan verbalisera
denna beskrivning. Men när vi hör en melodi kan vi direkt skilja den
från slumptoner och vi kan minnas den genom att dess beskrivning i
kodvärlden är så kort att den kan rymmas i vårt minne även om vi inte
är medvetna om hur denna inlagring i minnet görs.
För att vi skall kunna beräkna Zip och Struct måste vi finna den kortast
möjliga beskrivningen i kodvärlden, en beskrivning som utnyttjar alla
möjligheter att komprimera beskrivningen i symbolvärlden. I matematiskt
språk eftersträvar vi uttrycksformer som är entydiga utan att innehålla
något överflödigt. Det är därför, i många fall, lämpligt att använda
matematik i kodvärlden men vi måste vara medvetna om att den matematik
vi behärskar är bara en primitiv "pidginmatematik".
Vi kan alltså definiera begreppen Zip och Struct (och även andra begrepp)
och vi kan ange hur de skall beräknas men våra möjligheter att verkligen
komma fram till användbara kvantitativa värden är begränsade. Vår kunskap
om matematiskt språk är så bristfällig att det blir ungefär som om
Aristoteles hade försökt konstruera en elräkning.
Vad är potential ?
==================
Placera en kula på ett bord.Den har nu en potentiell energi som
vi kan utlösa genom att låta den rulla över bordskanten.Genom
lång erfarenhet har vi lärt oss att när en kula rullar över en
bordskant inträffar den förutsebara förändringen att den faller
till golvet.
Vi säger att kulans höjd över golvet är dess potential.Genom att
multiplicera denna potential med kulans tyngd får vi dess poten-
tiella energi.
För förmål i ett rum är det rimligt att använda höjd över golv
som potential.Om kulan faller från bordet ner på en stol utlöses
bara en del av den potentiella energin.När den ligger på stolen
har den ju kvar en del av sin potentiella energi eftersom vi kan
låta den rulla vidare ner till golvet.Höjden över golvet d v s
potentialen har alltså minskat och denna potentialskillnad gånger
kulans tyngd har omvandlats till en förutsägbar förändring när
kulan föll ned på stolen.
För alla föremål i rummet är golvet en lämplig referensnivå för
potential.Men öppnar vi balkongdörren kan vi låta kulan rulla
över balkongkanten och ned på marken.Med öppen balkongdörr blir
marken en lämpligare nollnivå för potential än golvet.
För kulan i rummet är tillståndet att den ligger på bordet en
osannolik avvikelse från det mest sannolika tillståndet att den
ligger på golvet.Osannolik avvikelse är potentiell energi som kan
omvandlas i energi d v s i en förutsägbar förändring när kulan
får falla mot golvet.Avvikelsen från nollnivån d v s i detta fall
höjden över golvet kallar vi potential.
När potentialen ändras frigörs (eller upptas) en energimängd som
är direkt proportionell mot potentialändringen.
När man skall rita en karta vill man kanske ange höjdskillnader
mellan punkterna A , B , C och D.Man kan då vid A skriva ut
höjden över B,höjden över C och höjden över D.Vid B kan man
skriva ut höjden över A,höjden över C och höjden över D.Och på
samma sätt kan man göra vid C och D.Har man många punkter blir
detta sätt opraktiskt.Det är lättare att ange höjden över havet
för var och en av punkterna och sedan räkna ut höjdskillnaderna
när man vill veta dem.I stället för att ange alla tänkbara
potentialskillnader anger vi alltså varje punkts potential och
räknar ut de potentialskillnader vi är intresserade av.
Ett annat exempel på potential är temperatur.När vi säger att te-
vattnet på spisplattan har blivit sextio grader varmare talar vi
om en potentialskillnad.Säger vi däremot att det har kommit upp
till åttio grader talar vi om en potential med nollnivån vid
vattnets fryspunkt.Och säger vi att det kommit upp till 353
grader Kelvin talar vi om en potential med nollnivån vid absoluta
nollpunkten.
�
Vad är absolut nollpunkt ?
==========================
Potentiell energi E är
E = S T
där
S = Mängd
T = Potential
Vi kan mäta ändringar av E , S och T men i många fall kan vi inte
direkt mäta absolutvärden av E och T.Om vi kan ändra S och T
oberoende av varandra kan vi emellertid bestämma absolutvärden på
följande sätt.
Håll T konstant och ändra S med ∆S.Mät ändringen av E som då
blir ∆E.Absolutvärdet av T blir då ∆E/∆S.
Metoden förefaller enkel men i verkligheten blir det ofta mer
komplicerat än så.Antag t ex att vi vill bestämma ett absolut
värde på elektrisk potential.Det skulle vi kunna göra genom att
skapa elektrisk laddning och se hur mycket energi som åtgår för
det.Men om vi vill skapa elektrisk laddning måste vi skapa
elektroner och de är inte bara elektrisk laddning,de har också
massa.Så hur skall vi veta hur mycket energi som åtgick för att
skapa elektronernas laddning?
Men i andra fall är det lättare.Om vi t ex skapar värme kan vi
öka värmeladdningen d v s entropin vid konstant temperatur och se
hur mycket energi som åtgår för det.På det sättet kan vi fast-
ställa en absolut temperaturskala som börjar vid den s k abso-
luta nollpunkten d v s -273,15 oC.
Ovanstående resonemang är något teoretiskt och tillrättalagt för
den principiella förståelsen av begreppet "absolut nollpunkt".I
själva verket kom man fram till den absoluta nollpunkten för
temperatur på ett betydligt mer handfast sätt.
Tryck och volym hos en gas är beroende av temperaturen.För en s k
ideal gas (en gas med små molekyler långt ifrån varandra och utan
kondensationstendenser) gäller att om man håller trycket konstant
varierar volymen linjärt med temperaturen (om man håller volymen
konstant är det istället trycket som varierar linjärt med tem-
peraturen).Sänker man temperaturen kommer man så småningom till
en punkt där volymen (eller trycket) blir noll.Om man kunde
fortsätta att sänka temperaturen skulle volymen (eller trycket)
bli negativ.Men eftersom vi inte kan föreställa oss negativ volym
eller negativt tryck måste det vara omöjligt att sänka temperatu-
ren från denna nivå.Det måste alltså vara absoluta nollpunkten
för temperatur.
Absolut nollpunkt för lägesenergi
=================================
När det gäller lägesenergi har man ansett att det inte finns
någon absolut potential.Om två partiklar attraherar varandra kan
vi naturligtvis tänka oss att de får närma sig till varandra
tills de sammanfaller.Lägesenergin i detta tvåpartikelsystem
minskar då och vi skulle kunna säga att den blir noll när
partiklarna sammanfaller.Men detta definierar inte någon absolut
nollpunkt för potentialen.Båda partiklarna kan ju påverkas av en
tredje partikel på sådant sätt att de fortfarande har lägesenergi
även när de sammanfaller.
För att fastställa absolut potential för lägesenergi skulle vi
kunna genomföra följande försök som är fullt tänkbart även om det
ställer orimliga (?) krav på mätnoggrannhet.
Ett föremål med massan m placeras på höjden h i ett gravitations-
fält med accelerationen g.Föremålet tillförs energin ∆W1 som
sätter det i rotation.Därvid ökar föremålets massa till m + ∆m.
Vi får
∆W1 = J w2 /2 + c2 ∆m
där c är ljushastigheten,J är tröghetsmomentet och w är vinkel-
frekvensen.Ökningen av massa medför ökning av tröghetsmomentet
och J avser alltså ett medelvärde av tröghetsmomentet från start
till slutvärde på rotationshastigheten.
Det roterande föremålet får så falla höjden ∆h i gravitations-
fältet.Därvid avges energin ∆W2
∆W2 = (m + ∆m)g ∆h
Föremålets rotation bromsas till stillestånd.Därvid avges enegin ∆W3
∆E3 = J w2 /2 + c2 ∆m
Föremålet lyfts höjden ∆h tillbaka till utgångspunkten.Därvid
tillförs energin ∆W4
∆W4 = m g ∆h
Vi skulle alltså för en komplett cykel få ut energin ∆W
∆W = ∆W2 + ∆W3 - ∆W1 - ∆W4
∆W = g ∆m ∆h > 0
Om J,m,c och w är konstanta när föremålet ändrar höjd avges allt-
så energin ∆W som inte har tillförts.Anordningen skulle alltså
vara ett perpetum mobile av första slaget.Om vi utgår från att
ett sådant inte är möjligt måste alltså J,m,c eller w minska när
föremålet faller i gravitationsfältet.För att bestämma nollpunkt
för en absolut potential kan man då tänka sig att låta föremålet
falla i ett gravitaionsfält tills den storhet som ändras blir
noll.
Hypotes:
Massa kan betraktas som kapacitans,massa gånger ljushastig-
het som laddning (=extensiv faktor) och ljushastighet som
potential för lägesenergi.
Vid de processer vi vanligen använder är förändringar i ljus-
hastigheten så obetydliga att vi kan anse att ljushastigheten är
konstant.Massa kan då användas som mått på laddning d v s som
extensiv faktor på det sätt som vi vanligtvis behandlar läges-
energi.
Energin hos massan m i punkt 1 kan skrivas som
W1 = m c12
Om massan får falla höjden ∆h i ett konstant gravitationsfält
med accelerationen g ändras dess energi till
W2 = m c22
Vi får då
W1 - W2 = m g ∆h
m c12 - m c22 = m g ∆h
c12 - c22 = g ∆h
Om vi sätter
c2 = c1 - ∆c
får vi
c12 - (c1 - ∆c)2 = 2 c1 ∆c - ∆c2
om ∆c << c1 får vi
2 c1 ∆c = g ∆h
∆c = g ∆h/(2 c1)
Om vi flyttar oss 1 m i jordens gravitationsfält ändras alltså
ljushastigheten med
∆c = 9,81x1/(2x3 108) = 1,6 10-8 m/s
Om vi befann oss i ett stort gravitationsfält som överallt hade
samma styrka som vid jordytan och ville nå absoluta nollpunkten
för lägesenergi skulle vi behöva flytta oss så att ∆c = c.För
ett så stort värde på ∆c gäller inte att ∆c << c.Vi måste
alltså även ta hänsyn till ∆c2 vilket ger
∆h = c2/g = 0,9 1016 m = 1 ljusår
Elementarpartiklar - små svarta hål
===================================
Betrakta en massa m0. Låt en annan massa m1 falla in mot m0.
Den kraft som verkar på m1 är
k m1 m0
F = ----------
r2
där r är avståndet mellan massorna och k är en sortomvandlingskonstant.
m1 kommer då att accelerera med accelerationen
F k m0
a = --- = -----
m1 r2
Accelerationen blir alltså oberoende av storleken på m1. Om man startar med
stort r kommer alltså alla massor, oberoende av storlek att falla på samma
sätt. De kommer alltså att ha acceleration och därmed även hastighet som
är entydigt bestämd av r.
När r närmar sig noll går acceleration och hastighet mot oändlighet. Hur
liten m0 än är kommer alltså hastigheten att nå ljushastighet
om inte m0 omges av en yta som kan växelverka med och stoppa
upp m1.
Varje massa som inte omges av ett skal som stoppar upp infallande partiklar
är alltså ett svart hål. Oberoende av massans storlek gäller att det finns
ett avstånd från masscentrum där infallande partiklar når ljushastighet
och omvänt d v s att en partikel måste ha ljushastighet för att kunna
lämna massan. Vid kortare avstånd är alltså flykthastigheten större än
ljushastigheten vilket innebär att ingen information kan nå oss därifrån.
Detta gäller även för så små massor som elektroner, protoner och neutroner.
En neutron är alltså helt enkelt ett mycket litet svart hål.
Vad är frihetsgrad?
===================
Minsta detekterbara förflyttning av minsta detekterbara mängd är
minsta detekterbara händelse.Vi kan kalla en sådan händelse för
ett händelsekvanta.
När vi arbetar med energi,d v s med förutsebara händelser,hante-
rar vi ofta kopplade händelser.När t ex en kula faller från ett
bord innebär det att ett stort antal händelsekvanta inträffar
inom en liten volym i rum-tid.Sannolikheten för dessa energi-
kvanta är kopplad så att om ett av dem inträffar ökar sanno-
likheten för alla de övriga.
Om händelse A är kopplad till händelse B,d v s om sannolikheten
för B ökar när A inträffar,tillhör A och B samma frihetsgrad.Om
däremot sannolikheten för B är oberoende av om A inträffar till-
hör de olika frihetsgrader.
Ett fast föremål har 6 rörelsefrihetsgrader.Det kan förflyttas i
rummet i tre av varandra oberoende riktningar och det kan rotera
kring tre av varandra oberoende axlar.Att en delmängd av föremå-
let faller nedåt påverkar sannolikheten för att även övriga del-
mängder skall falla nedåt men inte sannolikheten för att dessa
delmängder skall röra sig åt höger-vänster eller framåt-bakåt
eller att föremålet skall rotera.Fall nedåt är alltså en frihets-
grad som är skiljd från höger-vänsterrörelse,framåt-bakåtrörelse
och rotation.
Den olinjära etern
==================
Varför växelverkar två partiklar som kolliderar?
En partikel kan betraktas som ett vågpaket i etern.
Vanligtvis uppfattar vi etern som ett linjärt och förlustfritt
utbredningsmedium för vågor.
När två ljusstrålar korsas måste det innebära att fotoner passe-
rar genom varandra.Men genom att etern är linjär sker detta utan
att de växelverkar d v s ljusstrålarna passerar genom varandra
utan att de påverkar varandra.
För att skilja mellan olika radiosända program använder vi tekni-
ken att olika stationer sänder på olika frekvens.En radioantenn
nås alltså samtidigt av många olika vågor där vi med hjälp av ett
frekvensfilter kan sortera ut den signal vi vill ta emot.För att
detta skall vara möjligt måste den signal vi filtrerar fram vara
oberoende av signaler på andra frekvenser.Om etern är linjär blir
detta möjligt.
För att vågor skall kunna växelverka när de sammanfaller krävs
att utbredningsmediet är olinjärt.Att partiklar kan växelverka
betyder alltså att etern är olinjär.
Att fotoner kan passera genom varandra utan någon märkbar växet-
verkan medan elektroner och tyngre partiklar har en påtaglig
växelverkan när de kolliderar måste bero på att olinjariteten är
starkt amplitudbertoende.Det är först vid de höga amplituder som
förekommer i partiklar som elektroner som olinjariteten blir
påtaglig.
Hög amplitud ger alltså bottning beroende på att överföringsmedi-
et,d v s etern,mättas.ε och/eller µ är alltså amplitudberoende.
När en ljusstråle passerar en stjärna,t ex solen,böjs den in mot
stjärnan.Vid den sida av strålen som ligger närmast stjärnan är
alltså ljushastigheten lägre än vid strålens yttre kant.Men ljus-
hastigheten är c ~ 1/(ε µ). ε och/eller µ ökar alltså när man
närmar sig en stor massa som en stjärna.
Att etern är olinjär ger en,åtminstone kvalitativ,förklaring till
att vi kan ha stabila tillstånd t ex elementarpartiklar.Om ε och
µ varierar varierar även ljushastigheten vilket innebär variatio-
ner i brytningsindex som gör det möjligt att stänga in signaler
på liknande sätt som man kan stänga in en ljusstråle med hjälp av
totalreflektion i optiskt tunnare medium.
Man kan naturligtvis finna funktioner för ε och µ som resulterar
i de fenomen som vi kan observera.Men om dessa funktioner blir
allt för komplicerade ger de inget bidrag till våra försök att
finna en användbar världsbild.Frågan är därför:
Kan vi,genom att uppfatta ε och µ som enkla funktioner av
amplituden,åstadkomma en beskrivning av de fenomen vi
observerar?
Vi kan aldrig få veta hur världen egentligen är.Galileii världs-
bild är inte i någon absolut mening mera rätt än Ptolemaios.Dess
värde ligger i att den är enklare att använda.Vi är naturligtvis
intresserade av att beskriva världen sådan den ser ut från vår
utgångspunkt d v s med oss i centrum.Det är därför befogat att,
som Ptolemaios gjorde,välja en geocentrisk världsbild.För att en
heliocentrisk världsbild skall vara befogad måste den ha påtag-
liga fördelar.Och dess stora fördel är att den ger enkla beskriv-
ningar av planeternas rörelser.Man kunde tillämpa de enkla rörel-
selagar man funnit för föremål på jorden och därmed åstadkomma
mycket exakta beskrivningar av planetrörelser.Man behövde inte
formulera nya lagar för att beskriva planetrörelser.
På samma sätt gäller att det kan vara motiverat att uppfatta ε
och µ som funktioner av amplituden om vi därigenom kan beskriva
fenomen,t ex i atomer eller i rymden,med lagar som vi känner från
andra områden. Om detta är möjligt och hur dessa funktioner i så
fall ser ut vet vi emellertid inte.
�
Brahma,samsara,karma
====================
Det kan vara intressant att jämföra ovanstående synsätt med några
begrepp som förekommer i hinduismen t ex i Sankaras lära.
Hinduismens världsbild bygger visserligen på religiösa upplevel-
ser och den har utformats för att ange vägar (marga) till en
frälsning som för människan bortom denna världens ondska.Men en
del begrepp har ändå en påfallande likhet med ovanstående syn-
sätt.
I hinduismen finns det bakom den värld vi upplever med våra sin-
nen en annan,verkligare,värld som kallas brahma.
Vi kan inte med våra sinnen uppleva brahma.Endast genom religiös
upplevelse kan vi få kontakt med brahma.Denna kontakt kan vi söka
via två vägar,handlingarnas väg (karmamarga) eller insiktens väg
(jnanamarga).
Den verkliga,allomfattande verkligheten,brahma,kan vi alltså bara
komma i kontakt med via utomsinnliga vägar.Men brahma manifeste-
rar sig för våra sinnen som en stor illusion (maya) via ett tids-
flöde (samsara).
Via sina gärningar (karma) kan människan påverka maya.
Det finns alltså likheter mellan vårt energibegrepp och hinduer-
nas karma och mellan vårt tidsbegrepp och hinduernas samsara.Men
medan hinduerna strävar att komma förbi maya för att nå fram till
brahma struntar vi i det svåruppnåeliga brahma och intresserar
oss för att påverka maya.Därför nöjer vi oss inte med de kvalita-
tiva begreppen karma och samsara,vi har preciserat begreppen till
de kvantitativa storheterna energi och tid.
Hinduerna försökte nå fram till brahma via karmamarga men fann
att religiösa riter och andra symbolhandlingar var en svårfram-
komlig väg.Därför predikades jnanamarga som en bättre väg,man
sökte via gudshängivenhet (bhakti) komma fram på lättare sätt än
via den besvärliga handlingsvägen.
Västerlandet har,av dumhet eller av något annat skäl,hållit fast
vid karmamarga men mer och mer frångått det religiösa sättet att
bedömma handlingar till förmån för en bedömning som utgår från
den påtagliga påverkan på maya.Efter en lång och mödosam väg
under många århundraden finner vi nu att vi börjar se en verklig-
het som har vissa beröringspunkter med den som jnanamarga ledde
till.
�
Oändlighet
==========
I en jämnt fördelad eter kan inga punkter skiljas från varandra i
rummet och inga händelser skiljas från varandra i tiden.Rum och
tid existerar helt enkelt inte.Frågor som "Vad finns bortom?",
"Vad fanns före?" och "Vad kommer efter?" får ett "svar" genom
att frågorna blir meningslösa.
Den värld vi upplever (maya) är en störning (samsara) av den all-
uppfyllande,jämnt fördelade etern (brahma).
Störningen uppträder som vågpaket (partiklar) i etern.Dessa våg-
paket stör varandra genom att kollidera och därigenom uppräthålla
störningen.
Vi finner att vi kan definiera absoluta nollpunkter.Detta innebär
att vi kan få fram kvantitativa mått på samsaran.Vid absoluta
nollpunkten för temperatur står alla molekyler stilla i förhål-
lande till varandra och vid absoluta nollpunkten för lägesenergi
står alla fotoner stilla.Därmed har alla händelser upphört.
Genom att etern är olinjär finns en växelverkan mellan partiklar.
Denna avtar snabbt med avståndet men om ingenting stör ett parti-
kelpar finns en svag tendens till samordning av vågfunktionerna.
Om vi närmar oss absoluta nollpunkten kommer denna samordnings-
tendens att medföra att vågfunktionerna flyter ihop så att par-
tikelgränserna försvinner.Etern övergår då i en jämn fördelning.
Om gas strömmar i ett rör och vi kyler gasen finner vi att ström-
ningsegenskaperna förändras när gasen kondenserar till vätske-
droppar eller till fasta partiklar.Om elektroner strömmar i en
elektrisk ledare finner vi att strömningsegenskaperna förändras
när vi kyler ledaren så att elektronerna samordnas och "kondense-
rar" vid supraledning.Kyler vi materia till en temperatur som
ligger mycket nära absoluta nollpunkten finner vi att atomerna
samordnas till Bose-Einstein-materia.
Vår mödosamma väg via karmamarga har alltså gett oss möjlighet
att genom att närma oss absoluta nollpunkten få en liten glimt av
hur maya kan försvinna in i det alltuppfyllande brahma.Det har
tagit oss många århundraden och mycket arbete att nå det som man
via jnanamarga uppnått för länge sedan.Och om man ser möda som
något negativt har vi betett oss idiotiskt.Men det finns många
skäl att se mödan som något positivt.Vi har haft roligt under
resan och vi har på köpet fått många erfarenheter som vi har
uppskattat.
�
Ekonomi
=======
Vi har funnit att det finns vissa naturlagar som anger hur vår
omvärld fungerar.Läran om detta kallar vi fysik.
Även när det gäller samverkan mellan människor tycks det finnas
vissa lagar.Liksom inom fysiken gäller att ett stort antal slump-
mässiga händelser kan bilda sammanhållna mönster.Och även svaga
samordningstendenser kan få stor effekt på sådana mönster.
Läran om vilka lagar som anger hur smaverkna mellan människor
fungerar kallar vi ekonomi.
Den ekonomiska teorin har lånat en stor del av sin begrepps-
apparat från fysiken.
Det finns emellertid en mycket viktig skillnad mellan fysik och
ekonomi.Inom fysiken gäller att etern är mycket nära linjär vid
de låga amplituder som förekommer mellan partiklar på stort av-
stånd.Samordningstendensen mellan partiklar är därför mycket svag
och lätt att störa.Människor däremot kan mellan sig sprida ett
samordnande budskap snabbt och effektivt,speciellt med dagens
teknik för informationsspridning.
Trots detta finns det beröringspunkter som gjort jämförelser
användbara.
Fysikens samsara upprätthålls genom att partiklar kolliderar och
stör varandra.Ekonomins samsara upprätthålls av att vi,av lathet
och rädsla,inte lyckas samordna vår verksamhet.Vi ids inte och
vågar inte göra oss fria från individuella ambitioner.De flesta
religioner anvisar vägar för sådan ambitionsbefrielse men mycket
få är villiga att gå dem.Och varför skulle det vara eftersträ-
vansvärt?Det är samsaran som för oss framåt.Lathet och rädsla
håller oss kvar på karmamarga.Det är jobbigt men mycket roligare
än jnanamarga.Det är så roligt att det inte finns någon anledning
att söka efter genvägar.
Ekonomins roll är alltså inte att finna slutliga samhällslös-
ningar där lathet och rädsla eliminerats.Den är att hålla lathet
och rädsla på lagom nivå.Den lathet som får mig att konstruera
arbetsbesparande verktyg och den rädsla som får mig att så för
framtida skörd är stimulerande.Det är lathet och rädsla som höjer
mitt välbefinnande.Men när vi frammanar lathet genom att tala om
för människor att deras insats inte behövs eller frammanar rädsla
genom att låta människor svälta för att upprätthålla myten om den
materiella bristen,då har vi gått för långt.
(Mer om detta kommer i den planerade handboken för samhällsägare)
�
Karmamarga eller jnanamarga
===========================
Man kan spela golf på olika sätt.Man kan gå till utslagsplatserna
och mödosamt slå sig fram till hålen.Men man kan naturligtvis
också åka fram direkt till hålen och släppa ner bollen.
Om man löser korsord kan man prova sig igenom olika alternativ
tills man finner en lösning som fyller alla rutor.Men man kan
också vänta tills lösningen publiceras så att man direkt kan
skriva av lösningen.Det är mycket enklare och risken för fel blir
mycket mindre.
Om man läser matematik kan man arbeta sig igenom alla övnings-
exempel.Men man kan också slå upp facit och direkt skriva av lös-
ningarna.
Kroppen har ett belöningssystem med receptorer som fungerar som
Reset-Set-vippor (R-S-vippor).När dessa slår om från Reset till
Set (R -> S) upplever vi en välbefinnandekänsla.När de åter-
ställs,d v s vid S -> R upplever vi däremot ångest och andra
obehagskänslor.Det naturliga sättet att hantera detta system är
att vi sätter upp svåruppnåeliga mål som vi kan sträva mot och
koncentrera oss på så att vi inte märker när receptorerna går
S -> R.När vi så når ett mål får vi en kick när receptorerna går
R -> S.Men det finns många sätt att fuska.
Vi kan använda droger som stimulerar R -> S vilket ger en kick
utan att lösa problemet att hantera återställningen S -> R som är
nödvändig för framtida välbefinnandekänsla.
Vi kan också genom askes och självutplåning driva receptorerna
S -> R tills praktiskt taget alla gått över i läge R.Ju fler
receptorer som finns i läge R ju mindre stimulans krävs för att
ett påtagligt antal skall gå R -> S.Driver man denna metod till-
räckligt långt blir man hög av självplågeri.
Vill man inte använda sig av självplågeri kan man ersätta detta
med gudshängivenhet (bhakti).Man frigör sig från all koppling
till verkligheten och koncentrerar sig helt på en gudsupplevelse
som innebär omställning S -> R tills man uppnår spontan övergång
R -> S d v s tills man blir hög av sin världsfrånvändhet.
Jnanamarga innebär att man på detta sätt fuskar sig fram till en
upplevelse.Man når slutresultatet snabbt och effektivt.Det är som
att spela sig igenom en 18 håls golfbana på noll slag.
Av någon obegriplig anledning anses "heliga" män som släppt kon-
takten med verkligheten vara värda respekt.Av någon anledning
vägrar vi att ta dem för vad de uppenbarligen är d v s för
fuskare som försöker smita från verklighetens spelregler.
Faktum är att den katolska kyrkan kanske försökte göra en väl-
lovlig insats då den via inkvisitionen försökte bekämpa katarer-
na (kättarna) och deras reningslära.Men som vi vet spårade ink-
visitionen ur.Den var alltför användbar för helt andra syften.
För en enskild människa är det naturligtvis svårt att värja sig
mot någon som påstår sig ha fått instruktioner av en allsmäktig
gud och som beter sig på ett sätt som visar att han själv fak-
tiskt tror på det han säger.
Bakom inkvisitionens grundide låg troligen ett försök från ka-
tolska kyrkan att försöka hjälpa människor genom att använda
kyrkans auktoritet för att avfärda religiösa dumheter.Man för-
sökte bekämpa katarernas ide att man skulle renas genom att,som
"heliga" hinduer,dra sig undan från världen för att dö befriad
från all ondska.
Det är naturligtvis uppenbart att varken hinduernas föreställning
om jnanamarga som hedervärd eller katarernas reningslära kan
fungera som samhällsgrund.Lyckligtvis har de flesta människor en
sund önskan att göra världen bättre,inte att dra sig undan.För
det barbariska västerlandet har det varit viktigare att till-
fredsställa fysiologiska behov och att helt enkelt ha roligt än
att nå religiösa upplevelser.
APPENDIX
Laplacetransformen - Differentialkalkylens 'logaritm'
=====================================================
När jag vill bada i mitt badkar går jag in i badrummet och upptäcker att
vattenmängden i badkaret är noll.Så jämför jag detta observerade värde med
mitt önskemål,finner att det finns en skillnad mellan observerat värde och
önskat värde och låter denna skillnad bilda en felsignal som får mig att
öppna kranarna.De öppna kranarna ger ett vattenflöde som ökar vattenmängden
i karet vilket minskar felsignalen.När felsignalen blir noll stänger jag
kranarna.
Vattenmängden i karet är integralen av vattenflödet under den tid som jag
tappar i vatten.Och omvänt gäller att flödet är tidsderivatan av vattenmängden.
När vi försöker förändra vår omgivning så att den närmar sig våra önskemål
använder vi oss ofta av metoden att med flöden förändra mängder.Det kan handla
om allt från att fylla vatten i badkaret till att fylla magen med ett matflöde
tills den ger mättnadskänsla eller ladda ett bilbatteri med ett flöde av
laddningsbärare tills det blir fulladdat.
Om vi t ex vill ha en viss mängd (vatten i badkaret) och har möjlighet att
styra ett flöde (öppning av vattenkranarna) behöver vi hantera storheter
där den första är tidsintegral av den andra (eller omvänt där den andra är
tidsderivata av den första).
När vi försöker beräkna hur felsignalen förändras med tiden,t ex beräkna hur
lång tid det tar att fylla badkaret till önskad nivå,får vi alltså uttryck som
innehåller tidsderivator och tidsintegraler.Ekvationer som innehåller derivator
och integraler kallas för differentialekvationer.
När man vill beräkna hur någon storhet,t ex mängden vatten i badkaret,ändras
med tiden,behöver man ställa upp någon ekvation som gör att man kan lösa ut den
sökta storheten som funktion av tiden.Att ställa upp en sådan differentialekvation
kan vara nog så knepigt men det räcker inte med att ställa upp den,man måste lösa
den också.
Kan man förenkla uppställningen och lösningen av differentialekvationer?Om inte
för alla typer av differentialekvationer så kanske åtminstone för linjära
differentialekvationer? (Jag avstår,åtminstone t v,från att definiera begreppet
'linjära'.Läs det som 'många vanliga'.).
Newton utvecklade en metod för detta som han kallade 'fluxkalkyl'.Men han hemlighöll
hur han gjorde för att kunna imponera med sin förmåga att lösa problem som alla andra
gick bet på.Laplace presenterade senare en snarlik metod som blev allmänt accepterad
och används parallellt med det som ligger närmare Newtons metod och som idag kallas
operatorkalkyl.
Det handlar om metoder att ställa upp och lösa differentialekvationer i allmänhet,
inte bara ekvationer som beskriver tidsförlopp.Men studier av tidsfölopp är så ofta
förekommande att jag i fortsättningen förutsätter att det är det det är fråga om.
Om någonting är en funktion av tiden F(t) kan vi naturligtvis definiera en ny
funktion av en ny variabel f(s).Om vi binder samman dessa båda funktioner med
ett samband som gör att F(t) entydigt definierar f(s) kommer f(s) att beskriva
samma samband som F(t) men på ett nytt sätt.Vi säger då att f(s) är en transform
av F(t).
Vi kan t ex skapa en transform av F(t) som är en funktion av frekvens i stället för
en funktion av tid f(ω).Eftersom tid och frekvens är två olika sätt att se på
samma företeelse bekriver F(t) och f(ω) samma sak på olika sätt.
Före miniräknarnas tid var det besvärligt att multiplicera eller dividera långa tal
med varandra.Man överförde då talen till deras logaritmer,adderade respektive
subtraherade logaritmerna och överförde den resulterande logaritmen tillbaka till
resultatet av operationen.
Kan vi,på liknande sätt som vid logaritmräkning,överföra tidsfunktioner till
transformer som är lättare att räkna med,räkna med dessa och återföra resultatet
till den resulterande tidsfunktionen?Kan vi finna en "differentialkalkylens
logaritm"?
Att beräkna alla värden i en logaritmtabell är ett mödosamt arbete men det behöver
bara göras en gång.När man väl har räknat fram värdena är det bara att slå upp dem.
Man satte en mängd studenter på att räkna fram värden och skapade på det sättet
logaritmtabeller som man kunde använda utan att behöva bekymra sig över hur stort
arbete som låg bakom tabellvärdena.Att sedan datorerna kom och på bråkdelar
av en sekund gjorde de beräkningar som kostat studenter åratal av möda är en
annan sak.De allra flesta användarna brydde sig inte ens om att ta reda på hur
man gjorde för att räkna fram logaritmerna.På liknande sätt skulle man kunna
göra tabeller över transformer som man kan slå upp utan att behöva fundera på
hur man räknat fram dem.
Logaritmer överför multiplikation och division till addition och subtraktion.De
gör det alltså möjligt att använda enklare räknesätt.Går det att på motsvarande sätt
överföra derivering och integration till enklare räknesätt,t ex till multiplikation
och division?
Från elläran vet vi att spänningen över induktansen L är
u = L di/dt
och spänningen över kondensatorn C är
1
u = --- ∫ i dt
C
När vi räknar med växelström brukar vi använda oss av komplexa impedanser.Vi sätter
induktansens impedans till jωL och kondensatorns till 1/jωC.Och så räknar
vi efter de regler som gäller för likström.Vi sätter alltså
u = jω L i
resp
1
u = ---- i
jω C
Vi ersätter alltså derivering med multiplikation med jω och integration med
division med jω.Finns det någon transform som går att använda på det sättet
för alla tidsförlopp,d v s inte bara för sinusformad ström och spänning?Finns det
en transform f(s) till F(t) som har egenskapen att dF(t)/dt har transformen s f(s)
och ∫ F(t) dt har transformen f(s)/s ?
En transform som uppfyller dessa krav är
∞
⌠
f(s) = | e-st F(t) dt
⌡
0
Det är inte alltid som denna integral konvergerar så att man kan beräkna f(s) men
för många F(t) fungerar den.Hur denna beräkning går till behöver man sällan
bekymra sig om.Liksom logaritmer har färdigberäknade värden som man kan slå upp
har vanliga F(t) motsvarande färdigberäknade transformer som man kan slå upp.
CRC:s Standard Mathematical Tables har en bra sammanställning av Laplacetransformer.
Det finns också en annan variant av denna transform där man sätter
∞
f(p) ⌠
---- = | e-pt F(t) dt
p ⌡
0
När man använder denna brukar man kalla f(p) för operator.En bra beskrivning av
operatorkalkyl finns i Ingenjörshandboken del III A Teleteknik Allmän elektroteknik.
Några Laplacetransformer och operatorer
F(t) f(s) f(p)
A F(t) + B F(t) A f(s) + B f(s) A f(p) + B f(p)
dF(t)/dt s f(s) - F(0) p f(p) - p F(0)
1 1/s 1
t 1/s2 1/p
1 p
eat ------ ------
s - a p - a
Exempel: Vad är tidsderivatan av eat?
t = 0 ger F(0) = e0 = 1.Och laplacetransformen för eat är
1/(s-a).För att derivera multiplicerar man med s och subtraherar F(0).
Laplacetransformen för tidsderivatan blir alltså
s s s - a 1
----- - 1 = ----- - ----- = a ------
s - a s - a s - a s - a
Och den tidsfunktion som har denna laplacetrtansform är a eat
Tidsderivatan av eat är alltså a eat.
Det visste vi naturligtvis redan från början.Och exemplet är som att med
hjälp av logaritmer räkna ut att 3 gånger 7 är tjugo lite drygt.Men det
visar hur metoden fungerar.
Använder vi operatorer får vi på motsvarande sätt
p2 p2 p2 - a p p
----- - p = ----- - -------- = a ------
p - a p - a p - a p - a
Och den tidsfunktion som har denna operator är a eat.
Metoden fungerar alltså,åtminstone i detta fall.
Hur kan jag nu se på mitt badkar?
Jag kan se det som en 'black box' där jag skickar in en signal i form av ett
vattenflöde e(t) från kranarna.I badkaret omvandlas denna signal via
någon form av överföringsfunktion (G) till en vattenmängd c(t).Över-
föringsfunktionen åstadkommer en integrering av e(t) till
t
c(t) = ∫ e(t) dt
0
Fig 5
Den viktiga skillnaden mellan en transformator och en elektrisk vädur är att
transformatorn transformrar en växelspänning U1 till en annan spänning U2
där förhållandet mellan dessa båda spänningar bestäms av förhållandet
mellan antalet lindningsvarv i primärlindning och antalet lindningsvarv i
sekundärlindning. Stöthäverten, d v s väduren, däremot överför laddning från
matningsspänningen U1 till utspänningen U2 oberoende av vilket värde U2 har.
Om sorter
=========
Påståendet att 15 äpplen är 1 glas mjölk och 3 ostbitar är uppenbart nonsens.
Man kan inte lägga ihop mjölk och ost och än mindre få äpplen som resultat.
I exemplet ovan kan vi kalla 15 , 1 och 3 för mätetal och "äpplen" , "glas
mjölk" och "ostbitar" för sorter.Vanligtvis behöver vi hantera storheter av
varje sort för sig.Vi kan t ex säga att 10 äpplen plus 5 äpplen är 15 äpplen.
Alla termer skall alltså ha samma sort.
När man börjar läsa fysik är denna regel ett mycket användbart hjälpmedel för
att kontrollera beräkningar.När man ställer upp olika samband lär man sig att
alltid göra en sortkontroll d v s att se efter vilken sort de ingående termerna
har.Skulle någon term ha en annan sort än de övriga tyder det på att man gjort
något fel.Om man försöker lägga ihop längd mätt i meter med tid mätt i sekunder
har man troligen gjort något fel.
Våra måttsystem har utvecklats ur ungefärliga begrepp som volymen "tunna råg",
tiden "en halvdag",temperaturen "byxljummen" o s v.Men ökad köpenskap och ökad
rörlighet ställde krav på exaktare mätningar.Handlaren som köpte råg i tunnor
och sålde i påsar behövde veta hur många påsar det gick på en tunna.Och den
som skulle köra och hämta någon från tåget behövde veta när tåget skulle
komma.
Man började fundera på hur och vad vi kunde mäta.Till en början var det t ex
inte alls självklart att en fast mängd kunde mätas upp med samma typ av
volymmätning som användes för vätskor.Gjorde man en flätad måttkorg för att
mäta upp råg kunde den inte användas för vatten.Och om man sög upp vatten i
en mätkammare kunde man inte använda samma utrustning för att mäta upp råg.
Men så småningom enades vi om att sådana problem är av praktisk natur och
att de inte motsäger det principiella påståendet att det går att åstadkomma
volymmått som är användbara för såväl råg som vatten.Vi kunde göra oss av
med ett antal gamla mått och i stället mäta alla volymer i samma mått.
Så började man fundera på hur många olika sorter man behövde utgå ifrån för
att få fram alla sorter som man behövde i det dagliga livet.Om man hade bestämt
sig för en längd som fick utgöra längdenhet kunde man göra en kvadrat med denna
längdenhet som sida.Därigenom fick man en ytenhet utan att man behövde bestämma
sig för någon ny grundstorhet.Och man kunde åstadkomma en volymenhet genom att
göra en kub med längdenheten som sida.
Man kom till att man behövde enheter för längd,massa och tid för att kunna
härleda praktiskt taget alla de sorter man behövde.Vi fick cgs-systemet med
centimeter för längd,gram för massa och sekund för tid.
Om man skall kasta en sten gäller att kraften som man kastar med blir massan
gånger accelerationen.Hastighet är förflyttning per sekund och har alltså sorten
cm/s.Accelerationen är hastighetsändring per sekund och får alltså sorten cm/s2.
Massan mäts i gram och sorten för kraft blir alltså g cm/s2.Denna sort kan man
använda för alla krafter oavsett om de sätter fart på en kaststen eller lyfter
mjölsäckar.
En nackdel med cgs-systemet var att det inte gav en enhetlig behandling av
elektriska storheter.Man kunde dels utgå från elektrostatisk kraftverkan mellan
laddade partiklar dels från magnetisk kraftverkan mellan elektriskt laddade
partiklar i rörelse.Resultatet blev två måttsystem ese (elektrostatiska enheter)
och eme (elektromagnetiska enheter).Dessutom fick man ofta räkna med obekvämt
många nollor för storheter av alldaglig storhet.
Resultatet blev att man övergick till MKSA-systemet baserat på meter,kilogram,
sekund och ampere.Genom att lägga till ampere fick man en enhetlig behandling
av elektriska storheter.
Under en tid användes även det s k tekniska systemet som inte hade massa utan
kraft som en grundenhet.I stället för kilogram använde man tyngden av ett
kilogram som grundenhet.Men resultatet blev att många fick svårt att skilja
mellan massa och kraft.Fortfarande ser man manometrar graderade i kg/cm2 när
man naturligtvis menar kp/cm2 där kp (kilopond) är tyngden (=den kraft
som jordens dragningskraft ger) av ett kg.
Efter vissa justeringar blev MKSA-systemet internationell standard och döptes
om till SI-systemet.
Multiplicera en tid som har sorten s med en hastighet som har sorten m/s så får
resultatet sorten s m/s. Förkorta med s så ser man att resultatet får sorten m
vilket innebär att det är en längd.Tid gånger hastighet ger alltså längd.Vet man
hur lång tid en bil kör och med vilken hastighet den går kan man alltså räkna ut
hur långt den kommer.
Multiplicerar man en tid (s) med en kraft (kg m/s2) och dividerar med en massa
(kg) får resultatet sorten m/s.Resultatet blir alltså en hastighet.Om man vet hur
stor massa den sten man kastar har,hur lång tid kastet tar och vilken kraft man
kastar med kan man alltså räkna ut stenens utgångshastighet.
Ett sätt att lösa gymnasietidens övningsuppgifter och skrivningar var,åtminstone på
min gymnasietid,att se efter
Vilka storheter är givna och vad har de för sorter
Vilka storheter efterfrågas och vad har de för sorter
Hur kan man kombinera givna storheter så att resultatet får efterfrågad sort
Det är naturligtvis inte alltid självklart vilken hastighet som hör ihop med vilken
tid och vilken massa som påverkas av vilken kraft men metoden brukade räcka för att
ge godkänt även om man inte hade någon aning om vad man gjorde.
Metoden gav god utdelning för minimalt arbete och efteråt har jag förstått att jag
faktiskt lärde mig mer än de som mödosamt pluggade in alla formler och regler.
Måttsystem
==========
Om man vill mäta längden på en sträcka kan man lägga ena tummen vid ändpunkten.Så
lägger man den andra tummen intill,"vandrar" med tummarna bort till andra ändpunkten
och räknar antalet tumbredder.Är det fråga om en lite längre sträcka kan man sätta
hälen vid ena ändpunkten,"vandra" tå mot häl till andra ändpunkten och räkna antalet
fotlängder.
Detta är ett praktiskt sätt som vi nog har medfött.Och för sortomvandlingen mellan
tum och fot använde man sig av att det går 12 tum på en fot.Tolv är ett utmärkt
sortomvandlingstal som är jämnt delbart med 2,3,4 och 6.
För volym och vikt utgick man från vad man kunde lyfta,hur mycket man kunde dricka
o dyl.Tid angav man ofta i den tid som åtgick för någon vardaglig händelse o s v.
Detta var praktiskt men inexakt.Människor hade olika breda tummar och olika långa
fötter.Med franska revolutionen kom en ny syn på mått och vikt.Man släppte kravet
på anknytning till dagligt bruk och satte sig vid skrivbordet för att konstruera
"rationella" mått.
Vid skrivbordet föreföll tio vara bättre än tolv för omräkning mellan olika mått
av samma slag.Man skapade därför ett system med tiopotens-multiplar för att
åstadkomma hanterliga mått.Vårt talsystem har tio som bas därför att vi räknat
på våra tio fingrar (utom danskarna som även räknat på tårna).Men tio är bara
jämnt delbart med 2 och 5 vilket bl a ger problem med den,i praktiken ofta
förekommande,divisionen med 3.
Så skulle man överge tum som längdmått och i stället välja en längdenhet som alla
hade tillgång till och som var exakt lika lång för alla.Vid skrivbordet kan man
se jorden som tillgänglig för alla.Man utgick därför från jordens omkrets.Men det
blev en så opraktiskt stor enhet att man t o m vid skrivbordet insåg att man
måste välja en mindre del.Man delade därför in omkretsen i fyra kvadranter och
definierade längdenheten meter som en tiomiljontedel av en sådan kvadrant d v s
som en fyrtiomiljontedel av jordens omkrets.
Det låg också något av en tanke i att använda jordrotationen för att definiera en
tidsenhet d v s att låta sekund vara en viss del av dygnet och att använda jordens
omkrets för att fastställa en längdenhet.På det viset knöt man både längd och
tid till jordklotet.
Nu hade man fått en exakt och för alla lika längdenhet.Nu var det bara att sätta
igång och tillverka meterstavar för praktiska mätningar.Man skickade ut lantmätare
för att mäta upp jordens omkrets och fastställa meterns längd.De mätte men
det där med exakthet var inte så enkelt i verkligheten.När man hade prånglat ut
alltför många meterstavar för att kunna ta tillbaks dem började man förstå att
mätningarna var så felgjorda att man inte kunde behålla den ursprungliga
definitionen.
Det stolta meterprojektet,skrivbordsförnuftets triumf över vardagen,flaggskeppet i
krämarnas uppror mot adeln,hade havererat.
Nu gällde det att rädda ansiktet.Man gjorde en arkivmeter (antagligen tog man
helt enkelt någon prototyp till meterstav) som stämde väl med de meterstavar
man prånglat ut och förkunnade att en meter var arkivmeterns längd.Och man
vände sig till Napoleon.Han förfogade över argument av annat slag och kunde
sprida metersystemet utan några besvärande frågor om varför arkivmetern hade
just den längden.England och USA,som inte kom under Napoleons välde,behöll
tumsystemet långt in på 1900-talet.
Som enhet för massa tänkte man sig att använda gram definierat som massan hos
en kubikcentimeter vatten.Men även här övergick man till att knyta definitionen
till en arkivenhet.
Det här med arkivmeter och arkivkilogram fungerade hjälpligt men det smakade lite
nederlag om det.Krämarna hade inte lyckats lyfta sig över sin praktiska användning
av mätstickor och vikter för att skapa ett måttsystem som förankrats i något högre
än vardagens triviala utminutering av handelsbodens produkter.
Men om vi kunde finna någon universell,överallt och för alla lika hastighet skulle
vi kunna koppla längd och tid till varandra.Vi skulle kunna multiplicera tidsenheten
med denna hastighet och få en längd som vi kunde använda för att definiera en
längdenhet.
Ljushastigheten är en sådan universell hastighet och idag knyter vi tidsenheten till
periodtiden och längdenheten till våglängden för en viss spektrallinje.
På liknande sätt kan vi, med hjälp av Plancks konstant, knyta enheten för massa
till enheterna för längd och tid.
Och som framgår ovan är det möjligt att definiera en absolut tid i en,av våra
måttsystem oberoende,absolut enhet.För närvarande är våra möjligheter att mäta
denna enhet så dåliga att vi inte utnyttjar denna möjlighet.Vi vill inte göra
om fadäsen med mätningen av jordens omkrets.Men vi vet idag att det är möjligt
att skapa ett måttsystem som är helt fritt från godtyckliga arkivmått.
DEL 4
Etervinden
==========
Världen innehåller något. Detta "något" kan vi naturligtvis ge ett namn. Vi kan
kalla det gud, alluppfyllande Brahma, världseter eller något annat.
Låt oss döpa innehållet i världen till "Eter".
När vi bestämt oss för namnet är det dags att fastställa eterns egenskaper, att
finna egenskaper som liknar sådant som vi känner igen från den bild av världen
som våra sinnen ger oss.
I en värld med absolut jämnt fördelad eter kan inga punkter urskiljas i
rummet och inga händelser kan inträffa och ordnas i tid. Rum och tid
saknar mening i en sådan värld. Etern måste alltså ha egenskapen att den
kan störas så att den avviker från omgivningen. Det är sådana störningar
som ger begreppen "rum" och "tid" innebörd.
Om vi projicerar vår värld på ett koordinatsystem med tre rumsaxlar och
en koordinattidsaxel får vi en bild som är fullständig i den meningen att
två eterstörningar alltid växelverkar om de har samtliga koordinater lika
med varandra.
I en värld som står stilla, d v s som rör sig på samma sätt som observatören
växer koordinattiden i samma takt som parametertiden. Etern flödar alltså i
koordinattidsriktningen. Vår värld är alltså en etervind som (huvudsakligen)
blåser i koordinattidsriktningen.
Etervind kan beskrivas som en fyrdimensionell vektor c. Vi kan alltså se
världen som ett vektorfält där varje punkt tilldelas en fyrdimensionell
vektor som anger etervinden i punkten.
Vi har svårt att tänka i fyra dimensioner och projicerar därför ofta den
fyrdimensionella världsbilden på en tredimensionell bild med enbart
rumskoordinater. Vi uppfattar alltså en tredimensionell bild av en
fyrdimensionell etervind. Det vi uppfattar i denna är störningar som
svävar i vinden som ballonger eller moln i luft.
I den fyrdimensionella rymden kan vi lägga in ett cartesianskt koordinatsystem
med axlarna x , y , z och t. I det tredimensionella rummet kan vi lägga in
ett cartesianskt koordinatsystem med axlarna x , y och z. För att skilja
mellan den fyrdimensionella vektorn c och dess tredimensionella projektion
kan vi använda beteckningarna c4 och c3.
Så här kan vi naturligtvis göra men för att det skall vara någon mening med
det måste c4 och/eller c3 ha någon egenskap som är bekväm att
hantera. En sådan skulle kunna vara att det fyrdimensionella vektorfältet är
källfritt d v s att
div c4 = 0
En annan tänkbar egenskap skulle kunna vara att en störning av etern innebär
att
div c3 ≠ 0
Låt oss anta att det är så.
En eterstörning kallas "partikel".
För en vanlig partikel är div c3 < 0. En sådan partikel är alltså en sänka
för etervinden. Den är en uppvind i koordinattidsled som medför att etervinden
runt om den viker av in mot partikelcentrum. Denna inströmning mot centrum
kallas för gravitation.
Beloppet av c4 kallas för ljushastighet. Den ostörda etern strömmar alltså
med ljushastighet i koordinattidsled. Vid en partikel avlänkas strömnings-
riktningen så att vi får en hastighetskomposant i rumsled samtidigt som
hastigheten i koordinattidsled minskar.
Om inströmningen mot partikelcentrum sker i form av en virvel blir
rot c4 ≠ 0. I vanliga fall blir rot c4 en vektor i koordinat-
tidsriktning, d v s inströmningen sker i en virvel kring koordinattids-
axeln. Detta kallas elektrisk laddning.
Ballonger och moln som flyter omkring i atmosfären rör sig slumpmässigt
i förhållande till varandra. Men inte bara slumpmässigt. Luftrörelser
har en tendens att samordna sig till vindilar. På liknande sätt gäller att
partiklar som svävar i etern inte bara rör sig slumpmässigt i förhållande
till varandra. De har en tendens att ordna sig i mönster, ofta i mönster
som upprepas likt tapetmönster eller fjädermoln.
Små partiklar slår sig samman till större t ex till elektroner eller till
ännu störe som protoner och neutroner. Dessa slår sig i sin tur samman till
atomer som slår sig samman till molekyler som i sin tur bildat materia.
Sådan sammanslagning sker efter mycket säregna mönster. Uppenbarligen
följer mönsterbildningen mycket strikta och enkla regler men vi vet mycket
lite om dessa. Vi kan t ex observera att förhållandet mellan protonens
massa och elektronens massa alltid är 1800 men vi kan inte, med
utgångspunkt från andra kända egenskaper hos etern komma fram till detta
förhållande.
Bildade mönster har (ibland) en viss stabilitet. I ett stycke koppar ligger
kopparatomerna ordnade på bestämda platser som blommorna på en blommig
tapet. Detta mönster ändras inte även om vi förflyttar kopparstycket. För
att bryta mönstret får vi ta till verktyg med ännu stabilare mönster
t ex smältdegel, plåtsax eller såg.
Reglerna för mönsterbildning innefattar även regler för samband mellan
orsak och verkan.
Vi kan t ex ha ett mönster A där ett område med enbart kolatomer omges av
syremolekyler. Vi kan också ha ett mönster B där alla kolatomer ingår i
koldioxidmolekyler. Mönster A har en viss stabilitet och det kan bestå
trots att mönster B har större sannolikhet. Men om vi kan starta en
övergång från A till B i ett litet hörn av kolstycket kan vi få en spontan
fortsättning så att hela A övergår till B. Att tända på ett kolstycke i
ett hörn är alltså en orsak till en verkan som består i att hela kolstycket
brinner upp. De regler som gäller för övergång från A till B innehåller
alltså information om hur man kan orsaka d v s starta övergången.
Termodynamikens huvudsatser ger oss vissa regler för övergång mellan olika
mönster.
Vi har funnit att befintliga mönster kan ha en viss stabilitet men om
denna stabilitet bryts övergår de till mer sannolika mönster. Vår förmåga
inskränker sig till störa stabiliteten i befintliga system och därigenom
orsaka förändringar. Men med det kan vi komma långt. Om vi bara vet vad
som är ett mer sannolikt mönster kan vi arrangera förändringar så att de
motsvarar våra önskemål.
Högsta möjliga hastighet
========================
Universum är stort med många partiklar. Det gör att det blir svåröverskådligt.
Men de regler som gäller är, så vitt vi vet, samma som gäller för en liten
samling partiklar. Låt oss därför tänka oss ett litet universum med t ex
enbart 10 partiklar.
Läget för en partikel (A) i detta lilla universum bestäms av dess läge i
förhållande till de övriga 9 partiklarna. A:s läge anges alltså av 9 avstånd
till andra partiklar.
Om A ändrar läge förändras alla dess 9 avstånd. Men ändringen påverkar även
alla övriga partiklars läge eftersom 1 av deras 9 avstånd ändras.
Vi kan dela in A:s lägesförändring i steg som vart och ett omfattar minsta
detekterbar lägesförändring. Den minsta detekterbara lägesförändringen kan vi
kalla en längdenhet.
Varje gång någon partikel, t ex A, flyttas en längdenhet inträffar en
förändring som är minsta detekterbara förändring. En sådan förändring kallar
vi för händelseenhet eller enhetshändelse. Om A flyttas en längdeenhet
inträffar alltså en händelseenhet som berör A men den berör även alla andra
partiklar eftersom deras avstånd till A förändras. En händelse som berör A
innebär alltså en förändring för alla 10 partiklarna. Vi säger att tiden
går en tidsenhet för alla 10 partiklarna.
Om A flyttas 100 längdenheter och övriga partiklar ligger stilla inträffar
alltså 100 händelseenheter som innebär att tiden går 100 tidsenheter. A:s
hastighet blir då 100/100 = 1 längdenhet/tidsenhet. Detta är den teoretiskt
sett högsta hastighet som A kan ha.
Om A flyttas 100 längdenheter under det att B flyttas 200 längdenheter, C
flyttas 50 längdenheter och övriga partiklar ligger stilla inträffar
100 + 200 + 50 händelseenheter under A:s förflyttning. Tiden går alltså
350 tidsenheter och A:s hastighet blir 100/350 = 0,29 längdenheter/tidsenhet.
Om alla 10 partiklarna är lika och med samma sannolikhet för lägesförändring
kommer partikel A att, i genomsnitt, ändra läge var tionde gång. Den och alla
de andra partiklarna får då hastigheten 1/10 = 0,1 längdenheter/tidsenhet.
Alla partiklar rör sig då med hastigheten 0,1 längdenheter/tidsenhet men om
rörelseriktningen är helt slumpmässig kommer de bara att röra sig någon
längdenhet fram och tillbaka. De kommer alltså att ligga stilla om man
betraktar dem med en upplösning i längd på några tusen längdenheter. Då kommer
man enbart att se en rörelse hos de partiklar där rörelseriktningen inte
är helt slumpmässig.
Om vårt universum innehåller 10364 kvanta blir hastigheten för varje
kvanta 10-364 längdenheter/tidsenhet. Ett kvanta som ständigt rör sig
åt samma håll ser, vid låg upplösning, ut att röra sig medan de kvanta som rör
sig slumpmässigt åt olika håll ser ut att stå stilla.
Ett kvanta som rör sig med 10-364 längdenheter/tidsenhet åt samma
håll har den högsta hastighet som kan uppnås genom koncentration av rörelse-
riktning till en enda riktning. Denna hastighet kallar vi ljushastighet.
Varje kvanta marscherar alltså taktfast. Genom att gå ett steg fram och ett
tillbaka kan det göra "På stället marsch" och genom att gå två steg fram och
ett tillbaka eller genom att gå fram i zig-zag kan det gå sakta framåt. Den
högsta hastigheten når det om varje steg tas rakt fram. Den hastigheten kallas
ljushastighet.
Men om man kan få ett kvanta att inte bara gå rakt fram utan också gå i otakt
med högre takt än omgivningen skulle det kunna få ännu högre hastighet.
Detta skulle alltså innebära att det finns en möjlig hastighet som är
10364 gånger högre än ljushastigheten. Att det kan ligga något i
Science Fiction författarnas dröm att vi en gång i tiden skulle kunna komma
runt de begränsningar som ljushastigheten sätter. Att ljusvallen skulle kunna
visa sig vara som ljudvallen, ett problem som ställt en rad krav men inte ett
oöverstigligt hinder.
Vad är mönster?
===============
Vi kan se världen som en struktur av möjliga kvantapositioner. Dessa är
antingen fyllda eller tomma. Vi kan kalla detta för "realvärlden".
För att beskriva realvärlden kan vi tilldela varje kvantaposition en bit
d v s en etta för fylld position och en nolla för tom position. Vi kan
kalla denna beskrivning för "symbolvärlden".
Symbolvärlden innehåller långt fler nollor än ettor. Den innehåller alltså
stora sjok med enbart nollor. Det ligger då nära till hands att ersätta
t ex en rad med en miljon nollor med ett tecken som betyder "Här följer
en miljon nollor". Genom att använda tecken av denna typ kan vi beskriva
världen med en beskrivning som är kortare än symbolvärlden. Vi kan kalla
en sådan komprimerad beskrivning för "kodvärlden".
Symbolvärlden innehåller så mycket fler nollor än ettor att det alltid är
möjligt att åstadkomma en fullständig och felfri kodvärld med färre tecken
än symbolvärlden. Om dessutom ettorna uppträder i ordnade grupper kan
kodvärlden minskas ytterligare. Det visar sig att ettor uppträder i
grupper som vi kallar elektroner, protoner och neutroner. Genom att i
kodvärlden införa tecken för elektroner, protoner och neutroner kan vi
väsentligt minska kodvärlden. En elektron och dess läge kan i kodvärlden
beskrivas med några tusen bits vilket är långt mindre än i symbolvälden
där det ingår ungefär 10244 ettor i en elektron.
Om vi betecknar antal tecken i symbolvärlden med Sy och antalet tecken i
kodvärlden med Ko kan vi definiera världens komprimerbarhet som
Sy - Ko
Zip = --------
Sy
Zip för hela eller för en del av världen antar värden mellan 0 och 1. Att
antalet nollor i symbolvärlden är mycket större än antalet ettor innebär
Zip alltid blir större än noll. Vi kan kalla det minsta värde som Zip kan
anta vid normal fördelning mellan ettor och nollor för Zipmin.
Att världen ordnar sig till ett mönster innebär att Zip ökar. Vi kan ange
hur organiserad världen eller en del av världen är genom att definiera
mönstergraden Struct enligt
Zip - Zipmin
Struct = -------------
1 - Zipmin
Ett problem med kodvärlden är att det kan finnas sätt att kortfattat
beskriva ett mönster utan att vi känner till hur en sådan beskrivning kan
göras. Ett exempel på detta är fraktaler. En fraktal ger en bild som vi
direkt upplever som ett ordnat mönster. Den har alltså Zip mycket nära
1 och högt Struct. Men för några årtionden sedan visste vi inte att
ett sådant mönster kunde beskrivas med en mycket kort beskrivning i
kodvärlden.
Om man ser på en fraktalbild utan att veta något om fraktaler ser man
direkt att det är fråga om ett ordnat mönster som alltså måste ha en
kort beskrivning i kodvärlden även om man inte vet hur denna beskrivning
ser ut. På liknande sätt har en melodi en kortare beskrivning i
kodvärlden än en rad slumpmässiga toner även om vi inte kan verbalisera
denna beskrivning. Men när vi hör en melodi kan vi direkt skilja den
från slumptoner och vi kan minnas den genom att dess beskrivning i
kodvärlden är så kort att den kan rymmas i vårt minne även om vi inte
är medvetna om hur denna inlagring i minnet görs.
För att vi skall kunna beräkna Zip och Struct måste vi finna den kortast
möjliga beskrivningen i kodvärlden, en beskrivning som utnyttjar alla
möjligheter att komprimera beskrivningen i symbolvärlden. I matematiskt
språk eftersträvar vi uttrycksformer som är entydiga utan att innehålla
något överflödigt. Det är därför, i många fall, lämpligt att använda
matematik i kodvärlden men vi måste vara medvetna om att den matematik
vi behärskar är bara en primitiv "pidginmatematik".
Vi kan alltså definiera begreppen Zip och Struct (och även andra begrepp)
och vi kan ange hur de skall beräknas men våra möjligheter att verkligen
komma fram till användbara kvantitativa värden är begränsade. Vår kunskap
om matematiskt språk är så bristfällig att det blir ungefär som om
Aristoteles hade försökt konstruera en elräkning.
Vad är potential ?
==================
Placera en kula på ett bord.Den har nu en potentiell energi som
vi kan utlösa genom att låta den rulla över bordskanten.Genom
lång erfarenhet har vi lärt oss att när en kula rullar över en
bordskant inträffar den förutsebara förändringen att den faller
till golvet.
Vi säger att kulans höjd över golvet är dess potential.Genom att
multiplicera denna potential med kulans tyngd får vi dess poten-
tiella energi.
För förmål i ett rum är det rimligt att använda höjd över golv
som potential.Om kulan faller från bordet ner på en stol utlöses
bara en del av den potentiella energin.När den ligger på stolen
har den ju kvar en del av sin potentiella energi eftersom vi kan
låta den rulla vidare ner till golvet.Höjden över golvet d v s
potentialen har alltså minskat och denna potentialskillnad gånger
kulans tyngd har omvandlats till en förutsägbar förändring när
kulan föll ned på stolen.
För alla föremål i rummet är golvet en lämplig referensnivå för
potential.Men öppnar vi balkongdörren kan vi låta kulan rulla
över balkongkanten och ned på marken.Med öppen balkongdörr blir
marken en lämpligare nollnivå för potential än golvet.
För kulan i rummet är tillståndet att den ligger på bordet en
osannolik avvikelse från det mest sannolika tillståndet att den
ligger på golvet.Osannolik avvikelse är potentiell energi som kan
omvandlas i energi d v s i en förutsägbar förändring när kulan
får falla mot golvet.Avvikelsen från nollnivån d v s i detta fall
höjden över golvet kallar vi potential.
När potentialen ändras frigörs (eller upptas) en energimängd som
är direkt proportionell mot potentialändringen.
När man skall rita en karta vill man kanske ange höjdskillnader
mellan punkterna A , B , C och D.Man kan då vid A skriva ut
höjden över B,höjden över C och höjden över D.Vid B kan man
skriva ut höjden över A,höjden över C och höjden över D.Och på
samma sätt kan man göra vid C och D.Har man många punkter blir
detta sätt opraktiskt.Det är lättare att ange höjden över havet
för var och en av punkterna och sedan räkna ut höjdskillnaderna
när man vill veta dem.I stället för att ange alla tänkbara
potentialskillnader anger vi alltså varje punkts potential och
räknar ut de potentialskillnader vi är intresserade av.
Ett annat exempel på potential är temperatur.När vi säger att te-
vattnet på spisplattan har blivit sextio grader varmare talar vi
om en potentialskillnad.Säger vi däremot att det har kommit upp
till åttio grader talar vi om en potential med nollnivån vid
vattnets fryspunkt.Och säger vi att det kommit upp till 353
grader Kelvin talar vi om en potential med nollnivån vid absoluta
nollpunkten.
�
Vad är absolut nollpunkt ?
==========================
Potentiell energi E är
E = S T
där
S = Mängd
T = Potential
Vi kan mäta ändringar av E , S och T men i många fall kan vi inte
direkt mäta absolutvärden av E och T.Om vi kan ändra S och T
oberoende av varandra kan vi emellertid bestämma absolutvärden på
följande sätt.
Håll T konstant och ändra S med ∆S.Mät ändringen av E som då
blir ∆E.Absolutvärdet av T blir då ∆E/∆S.
Metoden förefaller enkel men i verkligheten blir det ofta mer
komplicerat än så.Antag t ex att vi vill bestämma ett absolut
värde på elektrisk potential.Det skulle vi kunna göra genom att
skapa elektrisk laddning och se hur mycket energi som åtgår för
det.Men om vi vill skapa elektrisk laddning måste vi skapa
elektroner och de är inte bara elektrisk laddning,de har också
massa.Så hur skall vi veta hur mycket energi som åtgick för att
skapa elektronernas laddning?
Men i andra fall är det lättare.Om vi t ex skapar värme kan vi
öka värmeladdningen d v s entropin vid konstant temperatur och se
hur mycket energi som åtgår för det.På det sättet kan vi fast-
ställa en absolut temperaturskala som börjar vid den s k abso-
luta nollpunkten d v s -273,15 oC.
Ovanstående resonemang är något teoretiskt och tillrättalagt för
den principiella förståelsen av begreppet "absolut nollpunkt".I
själva verket kom man fram till den absoluta nollpunkten för
temperatur på ett betydligt mer handfast sätt.
Tryck och volym hos en gas är beroende av temperaturen.För en s k
ideal gas (en gas med små molekyler långt ifrån varandra och utan
kondensationstendenser) gäller att om man håller trycket konstant
varierar volymen linjärt med temperaturen (om man håller volymen
konstant är det istället trycket som varierar linjärt med tem-
peraturen).Sänker man temperaturen kommer man så småningom till
en punkt där volymen (eller trycket) blir noll.Om man kunde
fortsätta att sänka temperaturen skulle volymen (eller trycket)
bli negativ.Men eftersom vi inte kan föreställa oss negativ volym
eller negativt tryck måste det vara omöjligt att sänka temperatu-
ren från denna nivå.Det måste alltså vara absoluta nollpunkten
för temperatur.
Absolut nollpunkt för lägesenergi
=================================
När det gäller lägesenergi har man ansett att det inte finns
någon absolut potential.Om två partiklar attraherar varandra kan
vi naturligtvis tänka oss att de får närma sig till varandra
tills de sammanfaller.Lägesenergin i detta tvåpartikelsystem
minskar då och vi skulle kunna säga att den blir noll när
partiklarna sammanfaller.Men detta definierar inte någon absolut
nollpunkt för potentialen.Båda partiklarna kan ju påverkas av en
tredje partikel på sådant sätt att de fortfarande har lägesenergi
även när de sammanfaller.
För att fastställa absolut potential för lägesenergi skulle vi
kunna genomföra följande försök som är fullt tänkbart även om det
ställer orimliga (?) krav på mätnoggrannhet.
Ett föremål med massan m placeras på höjden h i ett gravitations-
fält med accelerationen g.Föremålet tillförs energin ∆W1 som
sätter det i rotation.Därvid ökar föremålets massa till m + ∆m.
Vi får
∆W1 = J w2 /2 + c2 ∆m
där c är ljushastigheten,J är tröghetsmomentet och w är vinkel-
frekvensen.Ökningen av massa medför ökning av tröghetsmomentet
och J avser alltså ett medelvärde av tröghetsmomentet från start
till slutvärde på rotationshastigheten.
Det roterande föremålet får så falla höjden ∆h i gravitations-
fältet.Därvid avges energin ∆W2
∆W2 = (m + ∆m)g ∆h
Föremålets rotation bromsas till stillestånd.Därvid avges enegin ∆W3
∆E3 = J w2 /2 + c2 ∆m
Föremålet lyfts höjden ∆h tillbaka till utgångspunkten.Därvid
tillförs energin ∆W4
∆W4 = m g ∆h
Vi skulle alltså för en komplett cykel få ut energin ∆W
∆W = ∆W2 + ∆W3 - ∆W1 - ∆W4
∆W = g ∆m ∆h > 0
Om J,m,c och w är konstanta när föremålet ändrar höjd avges allt-
så energin ∆W som inte har tillförts.Anordningen skulle alltså
vara ett perpetum mobile av första slaget.Om vi utgår från att
ett sådant inte är möjligt måste alltså J,m,c eller w minska när
föremålet faller i gravitationsfältet.För att bestämma nollpunkt
för en absolut potential kan man då tänka sig att låta föremålet
falla i ett gravitaionsfält tills den storhet som ändras blir
noll.
Hypotes:
Massa kan betraktas som kapacitans,massa gånger ljushastig-
het som laddning (=extensiv faktor) och ljushastighet som
potential för lägesenergi.
Vid de processer vi vanligen använder är förändringar i ljus-
hastigheten så obetydliga att vi kan anse att ljushastigheten är
konstant.Massa kan då användas som mått på laddning d v s som
extensiv faktor på det sätt som vi vanligtvis behandlar läges-
energi.
Energin hos massan m i punkt 1 kan skrivas som
W1 = m c12
Om massan får falla höjden ∆h i ett konstant gravitationsfält
med accelerationen g ändras dess energi till
W2 = m c22
Vi får då
W1 - W2 = m g ∆h
m c12 - m c22 = m g ∆h
c12 - c22 = g ∆h
Om vi sätter
c2 = c1 - ∆c
får vi
c12 - (c1 - ∆c)2 = 2 c1 ∆c - ∆c2
om ∆c << c1 får vi
2 c1 ∆c = g ∆h
∆c = g ∆h/(2 c1)
Om vi flyttar oss 1 m i jordens gravitationsfält ändras alltså
ljushastigheten med
∆c = 9,81x1/(2x3 108) = 1,6 10-8 m/s
Om vi befann oss i ett stort gravitationsfält som överallt hade
samma styrka som vid jordytan och ville nå absoluta nollpunkten
för lägesenergi skulle vi behöva flytta oss så att ∆c = c.För
ett så stort värde på ∆c gäller inte att ∆c << c.Vi måste
alltså även ta hänsyn till ∆c2 vilket ger
∆h = c2/g = 0,9 1016 m = 1 ljusår
Elementarpartiklar - små svarta hål
===================================
Betrakta en massa m0. Låt en annan massa m1 falla in mot m0.
Den kraft som verkar på m1 är
k m1 m0
F = ----------
r2
där r är avståndet mellan massorna och k är en sortomvandlingskonstant.
m1 kommer då att accelerera med accelerationen
F k m0
a = --- = -----
m1 r2
Accelerationen blir alltså oberoende av storleken på m1. Om man startar med
stort r kommer alltså alla massor, oberoende av storlek att falla på samma
sätt. De kommer alltså att ha acceleration och därmed även hastighet som
är entydigt bestämd av r.
När r närmar sig noll går acceleration och hastighet mot oändlighet. Hur
liten m0 än är kommer alltså hastigheten att nå ljushastighet
om inte m0 omges av en yta som kan växelverka med och stoppa
upp m1.
Varje massa som inte omges av ett skal som stoppar upp infallande partiklar
är alltså ett svart hål. Oberoende av massans storlek gäller att det finns
ett avstånd från masscentrum där infallande partiklar når ljushastighet
och omvänt d v s att en partikel måste ha ljushastighet för att kunna
lämna massan. Vid kortare avstånd är alltså flykthastigheten större än
ljushastigheten vilket innebär att ingen information kan nå oss därifrån.
Detta gäller även för så små massor som elektroner, protoner och neutroner.
En neutron är alltså helt enkelt ett mycket litet svart hål.
Vad är frihetsgrad?
===================
Minsta detekterbara förflyttning av minsta detekterbara mängd är
minsta detekterbara händelse.Vi kan kalla en sådan händelse för
ett händelsekvanta.
När vi arbetar med energi,d v s med förutsebara händelser,hante-
rar vi ofta kopplade händelser.När t ex en kula faller från ett
bord innebär det att ett stort antal händelsekvanta inträffar
inom en liten volym i rum-tid.Sannolikheten för dessa energi-
kvanta är kopplad så att om ett av dem inträffar ökar sanno-
likheten för alla de övriga.
Om händelse A är kopplad till händelse B,d v s om sannolikheten
för B ökar när A inträffar,tillhör A och B samma frihetsgrad.Om
däremot sannolikheten för B är oberoende av om A inträffar till-
hör de olika frihetsgrader.
Ett fast föremål har 6 rörelsefrihetsgrader.Det kan förflyttas i
rummet i tre av varandra oberoende riktningar och det kan rotera
kring tre av varandra oberoende axlar.Att en delmängd av föremå-
let faller nedåt påverkar sannolikheten för att även övriga del-
mängder skall falla nedåt men inte sannolikheten för att dessa
delmängder skall röra sig åt höger-vänster eller framåt-bakåt
eller att föremålet skall rotera.Fall nedåt är alltså en frihets-
grad som är skiljd från höger-vänsterrörelse,framåt-bakåtrörelse
och rotation.
Den olinjära etern
==================
Varför växelverkar två partiklar som kolliderar?
En partikel kan betraktas som ett vågpaket i etern.
Vanligtvis uppfattar vi etern som ett linjärt och förlustfritt
utbredningsmedium för vågor.
När två ljusstrålar korsas måste det innebära att fotoner passe-
rar genom varandra.Men genom att etern är linjär sker detta utan
att de växelverkar d v s ljusstrålarna passerar genom varandra
utan att de påverkar varandra.
För att skilja mellan olika radiosända program använder vi tekni-
ken att olika stationer sänder på olika frekvens.En radioantenn
nås alltså samtidigt av många olika vågor där vi med hjälp av ett
frekvensfilter kan sortera ut den signal vi vill ta emot.För att
detta skall vara möjligt måste den signal vi filtrerar fram vara
oberoende av signaler på andra frekvenser.Om etern är linjär blir
detta möjligt.
För att vågor skall kunna växelverka när de sammanfaller krävs
att utbredningsmediet är olinjärt.Att partiklar kan växelverka
betyder alltså att etern är olinjär.
Att fotoner kan passera genom varandra utan någon märkbar växet-
verkan medan elektroner och tyngre partiklar har en påtaglig
växelverkan när de kolliderar måste bero på att olinjariteten är
starkt amplitudbertoende.Det är först vid de höga amplituder som
förekommer i partiklar som elektroner som olinjariteten blir
påtaglig.
Hög amplitud ger alltså bottning beroende på att överföringsmedi-
et,d v s etern,mättas.ε och/eller µ är alltså amplitudberoende.
När en ljusstråle passerar en stjärna,t ex solen,böjs den in mot
stjärnan.Vid den sida av strålen som ligger närmast stjärnan är
alltså ljushastigheten lägre än vid strålens yttre kant.Men ljus-
hastigheten är c ~ 1/(ε µ). ε och/eller µ ökar alltså när man
närmar sig en stor massa som en stjärna.
Att etern är olinjär ger en,åtminstone kvalitativ,förklaring till
att vi kan ha stabila tillstånd t ex elementarpartiklar.Om ε och
µ varierar varierar även ljushastigheten vilket innebär variatio-
ner i brytningsindex som gör det möjligt att stänga in signaler
på liknande sätt som man kan stänga in en ljusstråle med hjälp av
totalreflektion i optiskt tunnare medium.
Man kan naturligtvis finna funktioner för ε och µ som resulterar
i de fenomen som vi kan observera.Men om dessa funktioner blir
allt för komplicerade ger de inget bidrag till våra försök att
finna en användbar världsbild.Frågan är därför:
Kan vi,genom att uppfatta ε och µ som enkla funktioner av
amplituden,åstadkomma en beskrivning av de fenomen vi
observerar?
Vi kan aldrig få veta hur världen egentligen är.Galileii världs-
bild är inte i någon absolut mening mera rätt än Ptolemaios.Dess
värde ligger i att den är enklare att använda.Vi är naturligtvis
intresserade av att beskriva världen sådan den ser ut från vår
utgångspunkt d v s med oss i centrum.Det är därför befogat att,
som Ptolemaios gjorde,välja en geocentrisk världsbild.För att en
heliocentrisk världsbild skall vara befogad måste den ha påtag-
liga fördelar.Och dess stora fördel är att den ger enkla beskriv-
ningar av planeternas rörelser.Man kunde tillämpa de enkla rörel-
selagar man funnit för föremål på jorden och därmed åstadkomma
mycket exakta beskrivningar av planetrörelser.Man behövde inte
formulera nya lagar för att beskriva planetrörelser.
På samma sätt gäller att det kan vara motiverat att uppfatta ε
och µ som funktioner av amplituden om vi därigenom kan beskriva
fenomen,t ex i atomer eller i rymden,med lagar som vi känner från
andra områden. Om detta är möjligt och hur dessa funktioner i så
fall ser ut vet vi emellertid inte.
�
Brahma,samsara,karma
====================
Det kan vara intressant att jämföra ovanstående synsätt med några
begrepp som förekommer i hinduismen t ex i Sankaras lära.
Hinduismens världsbild bygger visserligen på religiösa upplevel-
ser och den har utformats för att ange vägar (marga) till en
frälsning som för människan bortom denna världens ondska.Men en
del begrepp har ändå en påfallande likhet med ovanstående syn-
sätt.
I hinduismen finns det bakom den värld vi upplever med våra sin-
nen en annan,verkligare,värld som kallas brahma.
Vi kan inte med våra sinnen uppleva brahma.Endast genom religiös
upplevelse kan vi få kontakt med brahma.Denna kontakt kan vi söka
via två vägar,handlingarnas väg (karmamarga) eller insiktens väg
(jnanamarga).
Den verkliga,allomfattande verkligheten,brahma,kan vi alltså bara
komma i kontakt med via utomsinnliga vägar.Men brahma manifeste-
rar sig för våra sinnen som en stor illusion (maya) via ett tids-
flöde (samsara).
Via sina gärningar (karma) kan människan påverka maya.
Det finns alltså likheter mellan vårt energibegrepp och hinduer-
nas karma och mellan vårt tidsbegrepp och hinduernas samsara.Men
medan hinduerna strävar att komma förbi maya för att nå fram till
brahma struntar vi i det svåruppnåeliga brahma och intresserar
oss för att påverka maya.Därför nöjer vi oss inte med de kvalita-
tiva begreppen karma och samsara,vi har preciserat begreppen till
de kvantitativa storheterna energi och tid.
Hinduerna försökte nå fram till brahma via karmamarga men fann
att religiösa riter och andra symbolhandlingar var en svårfram-
komlig väg.Därför predikades jnanamarga som en bättre väg,man
sökte via gudshängivenhet (bhakti) komma fram på lättare sätt än
via den besvärliga handlingsvägen.
Västerlandet har,av dumhet eller av något annat skäl,hållit fast
vid karmamarga men mer och mer frångått det religiösa sättet att
bedömma handlingar till förmån för en bedömning som utgår från
den påtagliga påverkan på maya.Efter en lång och mödosam väg
under många århundraden finner vi nu att vi börjar se en verklig-
het som har vissa beröringspunkter med den som jnanamarga ledde
till.
�
Oändlighet
==========
I en jämnt fördelad eter kan inga punkter skiljas från varandra i
rummet och inga händelser skiljas från varandra i tiden.Rum och
tid existerar helt enkelt inte.Frågor som "Vad finns bortom?",
"Vad fanns före?" och "Vad kommer efter?" får ett "svar" genom
att frågorna blir meningslösa.
Den värld vi upplever (maya) är en störning (samsara) av den all-
uppfyllande,jämnt fördelade etern (brahma).
Störningen uppträder som vågpaket (partiklar) i etern.Dessa våg-
paket stör varandra genom att kollidera och därigenom uppräthålla
störningen.
Vi finner att vi kan definiera absoluta nollpunkter.Detta innebär
att vi kan få fram kvantitativa mått på samsaran.Vid absoluta
nollpunkten för temperatur står alla molekyler stilla i förhål-
lande till varandra och vid absoluta nollpunkten för lägesenergi
står alla fotoner stilla.Därmed har alla händelser upphört.
Genom att etern är olinjär finns en växelverkan mellan partiklar.
Denna avtar snabbt med avståndet men om ingenting stör ett parti-
kelpar finns en svag tendens till samordning av vågfunktionerna.
Om vi närmar oss absoluta nollpunkten kommer denna samordnings-
tendens att medföra att vågfunktionerna flyter ihop så att par-
tikelgränserna försvinner.Etern övergår då i en jämn fördelning.
Om gas strömmar i ett rör och vi kyler gasen finner vi att ström-
ningsegenskaperna förändras när gasen kondenserar till vätske-
droppar eller till fasta partiklar.Om elektroner strömmar i en
elektrisk ledare finner vi att strömningsegenskaperna förändras
när vi kyler ledaren så att elektronerna samordnas och "kondense-
rar" vid supraledning.Kyler vi materia till en temperatur som
ligger mycket nära absoluta nollpunkten finner vi att atomerna
samordnas till Bose-Einstein-materia.
Vår mödosamma väg via karmamarga har alltså gett oss möjlighet
att genom att närma oss absoluta nollpunkten få en liten glimt av
hur maya kan försvinna in i det alltuppfyllande brahma.Det har
tagit oss många århundraden och mycket arbete att nå det som man
via jnanamarga uppnått för länge sedan.Och om man ser möda som
något negativt har vi betett oss idiotiskt.Men det finns många
skäl att se mödan som något positivt.Vi har haft roligt under
resan och vi har på köpet fått många erfarenheter som vi har
uppskattat.
�
Ekonomi
=======
Vi har funnit att det finns vissa naturlagar som anger hur vår
omvärld fungerar.Läran om detta kallar vi fysik.
Även när det gäller samverkan mellan människor tycks det finnas
vissa lagar.Liksom inom fysiken gäller att ett stort antal slump-
mässiga händelser kan bilda sammanhållna mönster.Och även svaga
samordningstendenser kan få stor effekt på sådana mönster.
Läran om vilka lagar som anger hur smaverkna mellan människor
fungerar kallar vi ekonomi.
Den ekonomiska teorin har lånat en stor del av sin begrepps-
apparat från fysiken.
Det finns emellertid en mycket viktig skillnad mellan fysik och
ekonomi.Inom fysiken gäller att etern är mycket nära linjär vid
de låga amplituder som förekommer mellan partiklar på stort av-
stånd.Samordningstendensen mellan partiklar är därför mycket svag
och lätt att störa.Människor däremot kan mellan sig sprida ett
samordnande budskap snabbt och effektivt,speciellt med dagens
teknik för informationsspridning.
Trots detta finns det beröringspunkter som gjort jämförelser
användbara.
Fysikens samsara upprätthålls genom att partiklar kolliderar och
stör varandra.Ekonomins samsara upprätthålls av att vi,av lathet
och rädsla,inte lyckas samordna vår verksamhet.Vi ids inte och
vågar inte göra oss fria från individuella ambitioner.De flesta
religioner anvisar vägar för sådan ambitionsbefrielse men mycket
få är villiga att gå dem.Och varför skulle det vara eftersträ-
vansvärt?Det är samsaran som för oss framåt.Lathet och rädsla
håller oss kvar på karmamarga.Det är jobbigt men mycket roligare
än jnanamarga.Det är så roligt att det inte finns någon anledning
att söka efter genvägar.
Ekonomins roll är alltså inte att finna slutliga samhällslös-
ningar där lathet och rädsla eliminerats.Den är att hålla lathet
och rädsla på lagom nivå.Den lathet som får mig att konstruera
arbetsbesparande verktyg och den rädsla som får mig att så för
framtida skörd är stimulerande.Det är lathet och rädsla som höjer
mitt välbefinnande.Men när vi frammanar lathet genom att tala om
för människor att deras insats inte behövs eller frammanar rädsla
genom att låta människor svälta för att upprätthålla myten om den
materiella bristen,då har vi gått för långt.
(Mer om detta kommer i den planerade handboken för samhällsägare)
�
Karmamarga eller jnanamarga
===========================
Man kan spela golf på olika sätt.Man kan gå till utslagsplatserna
och mödosamt slå sig fram till hålen.Men man kan naturligtvis
också åka fram direkt till hålen och släppa ner bollen.
Om man löser korsord kan man prova sig igenom olika alternativ
tills man finner en lösning som fyller alla rutor.Men man kan
också vänta tills lösningen publiceras så att man direkt kan
skriva av lösningen.Det är mycket enklare och risken för fel blir
mycket mindre.
Om man läser matematik kan man arbeta sig igenom alla övnings-
exempel.Men man kan också slå upp facit och direkt skriva av lös-
ningarna.
Kroppen har ett belöningssystem med receptorer som fungerar som
Reset-Set-vippor (R-S-vippor).När dessa slår om från Reset till
Set (R -> S) upplever vi en välbefinnandekänsla.När de åter-
ställs,d v s vid S -> R upplever vi däremot ångest och andra
obehagskänslor.Det naturliga sättet att hantera detta system är
att vi sätter upp svåruppnåeliga mål som vi kan sträva mot och
koncentrera oss på så att vi inte märker när receptorerna går
S -> R.När vi så når ett mål får vi en kick när receptorerna går
R -> S.Men det finns många sätt att fuska.
Vi kan använda droger som stimulerar R -> S vilket ger en kick
utan att lösa problemet att hantera återställningen S -> R som är
nödvändig för framtida välbefinnandekänsla.
Vi kan också genom askes och självutplåning driva receptorerna
S -> R tills praktiskt taget alla gått över i läge R.Ju fler
receptorer som finns i läge R ju mindre stimulans krävs för att
ett påtagligt antal skall gå R -> S.Driver man denna metod till-
räckligt långt blir man hög av självplågeri.
Vill man inte använda sig av självplågeri kan man ersätta detta
med gudshängivenhet (bhakti).Man frigör sig från all koppling
till verkligheten och koncentrerar sig helt på en gudsupplevelse
som innebär omställning S -> R tills man uppnår spontan övergång
R -> S d v s tills man blir hög av sin världsfrånvändhet.
Jnanamarga innebär att man på detta sätt fuskar sig fram till en
upplevelse.Man når slutresultatet snabbt och effektivt.Det är som
att spela sig igenom en 18 håls golfbana på noll slag.
Av någon obegriplig anledning anses "heliga" män som släppt kon-
takten med verkligheten vara värda respekt.Av någon anledning
vägrar vi att ta dem för vad de uppenbarligen är d v s för
fuskare som försöker smita från verklighetens spelregler.
Faktum är att den katolska kyrkan kanske försökte göra en väl-
lovlig insats då den via inkvisitionen försökte bekämpa katarer-
na (kättarna) och deras reningslära.Men som vi vet spårade ink-
visitionen ur.Den var alltför användbar för helt andra syften.
För en enskild människa är det naturligtvis svårt att värja sig
mot någon som påstår sig ha fått instruktioner av en allsmäktig
gud och som beter sig på ett sätt som visar att han själv fak-
tiskt tror på det han säger.
Bakom inkvisitionens grundide låg troligen ett försök från ka-
tolska kyrkan att försöka hjälpa människor genom att använda
kyrkans auktoritet för att avfärda religiösa dumheter.Man för-
sökte bekämpa katarernas ide att man skulle renas genom att,som
"heliga" hinduer,dra sig undan från världen för att dö befriad
från all ondska.
Det är naturligtvis uppenbart att varken hinduernas föreställning
om jnanamarga som hedervärd eller katarernas reningslära kan
fungera som samhällsgrund.Lyckligtvis har de flesta människor en
sund önskan att göra världen bättre,inte att dra sig undan.För
det barbariska västerlandet har det varit viktigare att till-
fredsställa fysiologiska behov och att helt enkelt ha roligt än
att nå religiösa upplevelser.
APPENDIX
Laplacetransformen - Differentialkalkylens 'logaritm'
=====================================================
När jag vill bada i mitt badkar går jag in i badrummet och upptäcker att
vattenmängden i badkaret är noll.Så jämför jag detta observerade värde med
mitt önskemål,finner att det finns en skillnad mellan observerat värde och
önskat värde och låter denna skillnad bilda en felsignal som får mig att
öppna kranarna.De öppna kranarna ger ett vattenflöde som ökar vattenmängden
i karet vilket minskar felsignalen.När felsignalen blir noll stänger jag
kranarna.
Vattenmängden i karet är integralen av vattenflödet under den tid som jag
tappar i vatten.Och omvänt gäller att flödet är tidsderivatan av vattenmängden.
När vi försöker förändra vår omgivning så att den närmar sig våra önskemål
använder vi oss ofta av metoden att med flöden förändra mängder.Det kan handla
om allt från att fylla vatten i badkaret till att fylla magen med ett matflöde
tills den ger mättnadskänsla eller ladda ett bilbatteri med ett flöde av
laddningsbärare tills det blir fulladdat.
Om vi t ex vill ha en viss mängd (vatten i badkaret) och har möjlighet att
styra ett flöde (öppning av vattenkranarna) behöver vi hantera storheter
där den första är tidsintegral av den andra (eller omvänt där den andra är
tidsderivata av den första).
När vi försöker beräkna hur felsignalen förändras med tiden,t ex beräkna hur
lång tid det tar att fylla badkaret till önskad nivå,får vi alltså uttryck som
innehåller tidsderivator och tidsintegraler.Ekvationer som innehåller derivator
och integraler kallas för differentialekvationer.
När man vill beräkna hur någon storhet,t ex mängden vatten i badkaret,ändras
med tiden,behöver man ställa upp någon ekvation som gör att man kan lösa ut den
sökta storheten som funktion av tiden.Att ställa upp en sådan differentialekvation
kan vara nog så knepigt men det räcker inte med att ställa upp den,man måste lösa
den också.
Kan man förenkla uppställningen och lösningen av differentialekvationer?Om inte
för alla typer av differentialekvationer så kanske åtminstone för linjära
differentialekvationer? (Jag avstår,åtminstone t v,från att definiera begreppet
'linjära'.Läs det som 'många vanliga'.).
Newton utvecklade en metod för detta som han kallade 'fluxkalkyl'.Men han hemlighöll
hur han gjorde för att kunna imponera med sin förmåga att lösa problem som alla andra
gick bet på.Laplace presenterade senare en snarlik metod som blev allmänt accepterad
och används parallellt med det som ligger närmare Newtons metod och som idag kallas
operatorkalkyl.
Det handlar om metoder att ställa upp och lösa differentialekvationer i allmänhet,
inte bara ekvationer som beskriver tidsförlopp.Men studier av tidsfölopp är så ofta
förekommande att jag i fortsättningen förutsätter att det är det det är fråga om.
Om någonting är en funktion av tiden F(t) kan vi naturligtvis definiera en ny
funktion av en ny variabel f(s).Om vi binder samman dessa båda funktioner med
ett samband som gör att F(t) entydigt definierar f(s) kommer f(s) att beskriva
samma samband som F(t) men på ett nytt sätt.Vi säger då att f(s) är en transform
av F(t).
Vi kan t ex skapa en transform av F(t) som är en funktion av frekvens i stället för
en funktion av tid f(ω).Eftersom tid och frekvens är två olika sätt att se på
samma företeelse bekriver F(t) och f(ω) samma sak på olika sätt.
Före miniräknarnas tid var det besvärligt att multiplicera eller dividera långa tal
med varandra.Man överförde då talen till deras logaritmer,adderade respektive
subtraherade logaritmerna och överförde den resulterande logaritmen tillbaka till
resultatet av operationen.
Kan vi,på liknande sätt som vid logaritmräkning,överföra tidsfunktioner till
transformer som är lättare att räkna med,räkna med dessa och återföra resultatet
till den resulterande tidsfunktionen?Kan vi finna en "differentialkalkylens
logaritm"?
Att beräkna alla värden i en logaritmtabell är ett mödosamt arbete men det behöver
bara göras en gång.När man väl har räknat fram värdena är det bara att slå upp dem.
Man satte en mängd studenter på att räkna fram värden och skapade på det sättet
logaritmtabeller som man kunde använda utan att behöva bekymra sig över hur stort
arbete som låg bakom tabellvärdena.Att sedan datorerna kom och på bråkdelar
av en sekund gjorde de beräkningar som kostat studenter åratal av möda är en
annan sak.De allra flesta användarna brydde sig inte ens om att ta reda på hur
man gjorde för att räkna fram logaritmerna.På liknande sätt skulle man kunna
göra tabeller över transformer som man kan slå upp utan att behöva fundera på
hur man räknat fram dem.
Logaritmer överför multiplikation och division till addition och subtraktion.De
gör det alltså möjligt att använda enklare räknesätt.Går det att på motsvarande sätt
överföra derivering och integration till enklare räknesätt,t ex till multiplikation
och division?
Från elläran vet vi att spänningen över induktansen L är
u = L di/dt
och spänningen över kondensatorn C är
1
u = --- ∫ i dt
C
När vi räknar med växelström brukar vi använda oss av komplexa impedanser.Vi sätter
induktansens impedans till jωL och kondensatorns till 1/jωC.Och så räknar
vi efter de regler som gäller för likström.Vi sätter alltså
u = jω L i
resp
1
u = ---- i
jω C
Vi ersätter alltså derivering med multiplikation med jω och integration med
division med jω.Finns det någon transform som går att använda på det sättet
för alla tidsförlopp,d v s inte bara för sinusformad ström och spänning?Finns det
en transform f(s) till F(t) som har egenskapen att dF(t)/dt har transformen s f(s)
och ∫ F(t) dt har transformen f(s)/s ?
En transform som uppfyller dessa krav är
∞
⌠
f(s) = | e-st F(t) dt
⌡
0
Det är inte alltid som denna integral konvergerar så att man kan beräkna f(s) men
för många F(t) fungerar den.Hur denna beräkning går till behöver man sällan
bekymra sig om.Liksom logaritmer har färdigberäknade värden som man kan slå upp
har vanliga F(t) motsvarande färdigberäknade transformer som man kan slå upp.
CRC:s Standard Mathematical Tables har en bra sammanställning av Laplacetransformer.
Det finns också en annan variant av denna transform där man sätter
∞
f(p) ⌠
---- = | e-pt F(t) dt
p ⌡
0
När man använder denna brukar man kalla f(p) för operator.En bra beskrivning av
operatorkalkyl finns i Ingenjörshandboken del III A Teleteknik Allmän elektroteknik.
Några Laplacetransformer och operatorer
F(t) f(s) f(p)
A F(t) + B F(t) A f(s) + B f(s) A f(p) + B f(p)
dF(t)/dt s f(s) - F(0) p f(p) - p F(0)
1 1/s 1
t 1/s2 1/p
1 p
eat ------ ------
s - a p - a
Exempel: Vad är tidsderivatan av eat?
t = 0 ger F(0) = e0 = 1.Och laplacetransformen för eat är
1/(s-a).För att derivera multiplicerar man med s och subtraherar F(0).
Laplacetransformen för tidsderivatan blir alltså
s s s - a 1
----- - 1 = ----- - ----- = a ------
s - a s - a s - a s - a
Och den tidsfunktion som har denna laplacetrtansform är a eat
Tidsderivatan av eat är alltså a eat.
Det visste vi naturligtvis redan från början.Och exemplet är som att med
hjälp av logaritmer räkna ut att 3 gånger 7 är tjugo lite drygt.Men det
visar hur metoden fungerar.
Använder vi operatorer får vi på motsvarande sätt
p2 p2 p2 - a p p
----- - p = ----- - -------- = a ------
p - a p - a p - a p - a
Och den tidsfunktion som har denna operator är a eat.
Metoden fungerar alltså,åtminstone i detta fall.
Hur kan jag nu se på mitt badkar?
Jag kan se det som en 'black box' där jag skickar in en signal i form av ett
vattenflöde e(t) från kranarna.I badkaret omvandlas denna signal via
någon form av överföringsfunktion (G) till en vattenmängd c(t).Över-
föringsfunktionen åstadkommer en integrering av e(t) till
t
c(t) = ∫ e(t) dt
0
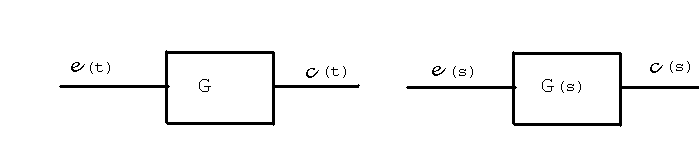 Fig 1
Om jag i stället använder laplacetransformerna överför jag integrationen till en
multiplikation med 1/s.Jag kan nu se det som att e multipliceras med G och ger
c enligt
e(s) G(s) = c(s)
Om jag öppnar kranarna till det konstanta flödet I (liter/sek) blir
e(s) = I 1/s = I/s
eftersom laplacetransformen för 1 är 1/s.
Överföringen är en integration vilket innebär att
G(s) = 1/s
vilket ger
I 1 1
c(s) = e(s) G(s) = --- --- = I ----
s s s2
Den tidsfunktion som motsvarar laplacetransformen 1/s2 är t.Vi får
alltså
c(t) = I t
Om man multiplicerar kranflödet i liter/sek med det antal sekunder man tappar får
man alltså vattenmängden.Det inser man naturligtvis direkt men det blir inte fel om
man försöker komma fram till resultatet med hjälp av laplacetransformen.Och när
e(t) och G blir mer komplicerade blir inte slutresultatet lika självklart.
Vektoranalys
============
Om man är intresserad av vindar finns det anledning att beskriva atmosfären
på sådant sätt att man kan dra slutsatser om vilka vindar som blåser, vilka
som kommer att blåsa och vilka som har blåst.
Vind är volymflöde som orsakas av tryckskillnad. Det kan alltså vara lämpligt
att beskriva atmosfären genom att ange trycket i ett antal olika punkter.
Tryck är en endimensionell vektor, d v s en skalar. Det räcker med att ange en
enda siffra för att ange trycket i en viss punkt. Denna siffra är tryck-
skillnaden mellan punkten och en absolut nollpunkt för tryck. Tryck är alltså
en potential, d v s en skalär storhet som anges som avvikelse från en nollpunkt.
Om vi beskriver atmosfären på detta sätt säger vi att den är ett potentialfält.
Om vi vet trycket p i varje punkt kan vi rita tryckkartor där vi sammanbinder
punkter med samma tryck till isobarer. På tvådimensionella kartor blir
isobarerna linjer och i tredimensionella kartor blir isobarerna ytor.
Men det är inte tryck utan tryckskillnad som driver vind. Att vi vet trycket i
en viss punkt räcker inte för att kunna säga om vinden ökar eller minskar i
punkten. Vi behöver veta hur trycket förändras i punktens omgivning.
För att beskriva tryckförändringar i punktens omgivning lägger vi in ett
treaxligt koordinatsystem med vinkelräta axlar (x , y , z) och origo i punkten.
Så går vi ett steg i x-riktningen och mäter upp tryckändringen dpx. Vi
dividerar med steglängden dx och får ett mått dpx/dx på hur snabbt trycket
ändras i x-riktningen. Så gör vi likadant i y-riktningen och i z-riktningen och
får tre siffror som anger hur snabbt trycket ändras i området runt punkten.
Vi kan alltså beskriva tryckändringen runt punkten med tre siffror d v s med en
tredimensionell vektor. Denna vektor kallas för gradient och anges med operatorn
grad. Vi kan alltså skriva
grad p = (dpx/dx dpy/dy dpz/dz)
Gradienten för en potential d v s för en skalar är alltså en vektor som anger hur
snabbt potentialen ändras i olika riktningar.
Vind är volymflöde genom ytenhet. För att mäta vinden kan vi göra en öppning med
ytan 1 m2 och se hur många m3 som passerar genom öppningen per sekund.
Sorten för vind blir då (m3/s)/m2 = m/s alltså en hastighet som vi kallar
vindhastighet. Vi betecknar vind d v s vindhastighet med v.
Vind har inte bara ett värde den har också en riktning. Den kan alltså inte som
ses som en skalär potential utan den måste behandlas som en vektor. Vi kan t ex
ange den genom att ange vind i x-riktningen (vx), vind i y-riktningen (vy) och
vind i z-riktningen (vz). Till varje punkt i atmosfären hör alltså en skalar
som anger trycket i punkten, en vektor som anger tryckändringen i punkten
och en vektor som anger vinden i punkten.
Vind i vindriktningen kallas för vindens belopp och betecknas |v|.
Vi omsluter en punkt med en sluten yta S t ex med en klotyta. Så delar vi upp
denna yta i smådelar dS som är så små att vinden kan anses vara lika i alla
delar av en sådan småyta. |v| dS cos α är då det volymflöde som strömmar ut
genom dS (α är vinkeln mellan v och normalen till dS). På en tidsenhet bortförs
alltså via dS luftvolymen |v| dS cos α från den volym som omsluts av S. Summerar
vi över alla dS får vi den luftvolym som varje tidsenhet bortförs från volymen
inom S. För att få ett mått som inte beror på hur stor volym V som S omsluter
dividerar vi med V. Vi har nu fått ett mått på hur mycket volym (observera
skillnaden mellan omsluten volym V och den flödande luftvolym v som kan
skapas) som skapas inom S och blåser ut utan att ha blåst in. Vi har alltså
fått ett mått på punkten som vindkälla. Detta anges med operatorn div som
alltså anger källstyrka.
I många fall gäller att den vind som blåser in i en punkt är lika stor som
den vind som blåser ut från punkten. Källstyrkan är då 0 och vi säger att
vinden källfri. Men om t ex solen värmer i punkten så att luftens volym ökar
kommer större volym att lämna punkten än den volym som kom in i punkten
(eftersom luft är kompressibel kommer även tryckändring att ge volymändring).
Vi får då div v > 0.
Ett flöde (t ex vind) av något (t ex luftvolym) kan alltså beskrivas som ett
vektorfält där varje punkt tilldelas en vektor (v) som anger flödets storlek i
olika riktningar. Divergensen för denna vektor (div v) anger källstyrkan för
det som flödar.
Div v, d v s källstyrkan, är en skalär storhet.
Inom ellära använder man Kirchhoffs första lag som säger att summan av alla
strömmar till en punkt är lika med summan av alla strömmar från punkten.
Kirchhoffs första lag säger alltså att strömmen är ett källfritt flöde. Vi
har alltså div I = 0 i alla punkter. Antalet laddningsbärare, d v s antalet
elektroner, som strömmar i ledningarna och utgör det flöde som är den
elektriska strömmen ändras alltså inte i någon punkt.
Maxwells ekvationer är en annan formulering av Kirchhoffs lagar och där har
Kirchhoffs första lag formen
div I = 0
Detta gäller om inte laddningsfördelningen ändras.
Vi kan ha både vind och elektrisk ström som varierar trots att källstyrkan är
noll. Men vi kan inte ha ett nettoflöde in i eller ut ur en punkt om käll-
styrkan är noll. För källor och sänkor i ett flöde är divergensen skiljd från
noll.
Små flöden kan flyta samman till ett stort och ett stort flöde kan grena sig i
många små även om källstyrkan är noll. Att källstyrkan i en punkt är större
än noll innebär att ett flöde uppstår i punkten utan att komma in i punkten
och att källstyrkan är mindre än noll innebär att ett flöde försvinner i
punkten.
Div v ≠ 0 betyder att en del av flödet v kommer från ingenstans eller
försvinner i intet. Vi kan naturligtvis säga att ett flöde kommer från eller
försvinner till en annan dimension. Om vi t ex studerar horisontella vindar
kan vi göra det i ett tvådimensionellt system med x-axeln i öst-väst och
y-axeln i nord-syd. Om vi då har div v ≠ 0 kan vi naturligtvis skriva
div v = dvz/dz och tolka det som att en del av v kommer från eller försvinner
till en tredje dimension (z). Om vi så lägger in en vertikal axel och kallar
den för z-axeln, d v s inför den tredje dimensionen som en vertikal
dimension tolkar vi vz som fallvind eller uppvind som tillför
eller bortför horisontell vind. Om detta var hela orsaken till att div v i det
tvådimensionella systemet var skiljd från noll blir div v = 0 i det
tredimensionella systemet. Skulle det dessutom finnas andra skäl,
t ex att uppvärmning ger volymutvidgning kommer div v inte att minska
ända till noll utan ha ett restvärde som vi kan tolka som kommande från
ytterligare en dimension.
Antag att vi är intresserade av en viss punkt A. Vi lägger in en plan yta
som innehåller A. Så går vi runt en sluten väg runt A i ytan. För varje steg
vi tar multiplicerar vi steglängden med vindhastigheten i stegriktningen.
Alla dessa produkter adderar vi tills vi är tillbaka till utgångspunkten. Vi
bildar alltså
S
∫ v dl
L
där
dl är steglängden och L betecknar en sluten väg
Värdet av denna integral beror på hur vi valt att lägga planet. Vi väljer så
det plan som ger maximalt värde på denna integral. Så dividerar vi med
den ytan som gångvägen omsluter och kallar det vi då får fram för beloppet
av rot v.
Om vi får lika mycket medvind som motvind när vi går runt en sluten väg är
rot v = 0. Vi säger då att vinden är virvelfri. Skulle det däremot blåsa en
virvelvind runt A kan vi följa med virveln och gå runt A så att vi hela vägen
får medvind. Vi beskriver detta med en vektor som kallas rot v som har
beloppet lika med ovanstående integral dividerad med den omslutna ytan
och riktningen sammanfallande med normalen till den omslutna ytan.
Ett exempel på ett praktiskt taget virvelfritt fält är gravitationen vid
markytan. Antag att vi går runt en sluten väg och för varje steg
multiplicerar tyngden med höjdändringen. När vi kommer tillbaka till
utgångspunkten och lägger ihop alla dessa produkter får vi det arbete
som uträttats under vägen och detta blir alltid noll hur vi än går. Det i
sin tur innebär att arbetet som uträttas när vi går från punkt A till punkt B
blir lika stort vilken väg vi än går. Vi kan då tilldela punkt A en potential
gA som motsvarar arbetet att föra en massenhet från en
referenspunkt till A. Och på motsvarande sätt kan vi tilldela punkt B en
potential gB. Arbetet att föra massan m från A till B blir
då W enligt
W = m gA - m gB = m (gA - gB)
Inom ellära använder man Kirchhoffs andra lag som säger att summan
av alla spänningar längs en sluten väg är noll, d v s att fältstyrkan är
virvelfri.
I Maxwells ekvationer har Kirchhoffs andra lag formuleringen
rot E = 0
(OBS att E här betyder elektrisk fältstyrka, inte energi)
Detta gäller om det inte finns några varierande magnetiska fält. Tids-
derivatan hos ett magnetiskt fält ger elektriska virvlar.
I ett tredimensionellt system är vi vana vid att se virvlar. Vi har alla sett
virvelvindar och virvlar när vattnet runner ur badkaret. I tre dimensioner
kan vi göra en uppdelning i ett plan och en axel vinkelrät mot planet. En
virvel runt denna axel kommer då att ligga i planet. För ett fyrdimensionellt
system tillkommer emellertid möjligheter som inte är helt lätta att före-
ställa sig. En virvel kring tidsaxeln kommer att ligga i rummet men inte
nödvändigtvis i ett plan.
Tensorkalkyl
============
Vi kan,som sagt,inte omvandla energi mellan olika former enbart genom att
flytta gränserna för de mängder vi betraktar.Världen kan inte veta hur vi
hittar på att dela upp den.
När vi lägger in koordinatsystem tilldelar vi varje punkt ett läge som anges
med ett antal koordinater.På en plan karta anger vi två koordinater,i rummet
anger vi tre koordinater och om vi tar med tiden så anger vi i rum-tiden fyra
koordinater.Vi säger att kartan är tvådimensionell,rummet tredimansionellt och
rum-tiden fyrdimensionell.Läget på en karta anges med en tvådimensionell
ortsvektor (två sammanhörande tal),i rummet med en tredimensionell ortsvektor
och i rum-tiden med en fyrdimensionell ortsvektor.
Om vi ändrar koordinatsystemet ändras ortsvektorerna.Men lika lite som världen
kan veta hur vi avgränsar våra mängder kan världen veta hur vi har hittat på
att lägga in våra koordinatsystem.Det som händer i världen måste alltså vara
oberoende av hur vi väljer att lägga in koordinatsystem.Vi säger att det finns
storheter som är invarianta under koordinattransformationer.
Lägg in ett treaxligt rätlinjigt och rätvinkligt koordinatsystem i huset.Lägg
origo vid golvet i sydvästra hörnet.Lägg x-axeln mot norr,y-axeln mot öster och
z-axeln rakt upp.Gradera axlarna i meter.Häng upp en termometer på en vägg.
Termometern får då koordinater t ex (3 , 4 , 1).
Behåll origo och z-axeln men vrid x-axel och därmed även y-axeln.Termometern får
då nya koordinater t ex (2 , 4,6 , 1).
Att vi på detta sätt ändrar koordinatsystemet skall naturligtvis inte påverka vad
termometern visar.Vi säger att temperaturen är invariant under koordinattransfor-
mationer.
Även om termometern har fått nya koordinater har den inte flyttats.Inte heller
origo har flyttats.Avståndet mellan termometern och origo måste alltså vara
oförändrat.Avstånd mellan punkter är invarianta under koordinattransformationer.
I första fallet är avståndet mellan termometern och origo 5,1 m.Om vi i andra
fallet har x = 2 och z = 1 måste alltså y ha ett värde som ger avståndet 5,1.Vi
kan då beräkna y och få det till 4,6.
Vi kan alltså inte välja nya värden på x och y hur som helst.Om vi vrider x-axeln
så att vi får en ny x-koordinat kan vi beräkna värdet på motsvarande y-koordinat.
Och har vi vridit så att vi fått nytt värde på termometerns koordinater så har
alla andra koordinater ändrats på beräkningsbart sätt.Vi kan inte fritt välja men
väl beräkna nya koordinater för stolar,bord,lampor o s v.
Vi anger termometerns läge genom att ange tre koordinater.Läget anges alltså med
tre siffror.Vi säger att termometerläget är en tredimensionell vektor.I många
läroböcker använder man pilar för att beskriva vektorer.Om vi vill tänka på denna
vektor som en pil ser vi den som en pil som startar i origo och slutar vid
termometern.Längden av denna pil kallar vi termometerns avstånd från origo.Det
blir alltså 5,1 m.
Om golvets sydvästra hörn ligger 6 m åt norr,8 m åt öster och 0,5 m över tomtens
sydvästra hörn kan vi parallellförflytta koordinatsystemet från golvets sydvästra
hörn till tomtens sysdvästra hörn.Koordinataxelriktningarna ändras då inte men
x-koordinaten ökar med 6 m,y-koordinaten ökar med 8 m och z-koordinaten ökar med
0,5 m.I stället för termometerläget (3 , 4 , 1) får vi då läget (9 , 12 , 1,5).En
sådan parallellförflyttning medför också att avståndet till origo förändras.
Parallellförflyttning av koordinatsystemet innebär alltså att termometerns avstånd
från origo ändras men däremot ändras inte avståndet mellan termometern och golvets
sydvästra hörn.Koordinaterna ändras men alla avstånd mellan verkliga punkter förblir
oförändrade.Avstånd från origo är ingen invariant storhet.Det är beroende av hur
vi väljer koordinatsystem.Avståndet mellan två fysiska föremål däremot är en
invariant storhet som måste vara oberoende av hur vi väljer koordinatsystem.
Om vi bara har gjort en parallellförflyttning d v s bara har förflyttat origo
får vi direkt att alla avstånd mellan föremål blir oförändrade.När vi drar
koordinaterna för det ena föremålet från koordinaterna för det andra försvinner
origoförflyttningen.Vi har alltså räknat bort origoförflyttningen när det blir
dags att kvadrera,addera och dra roten ur för att få fram avståndet.Men om vi
har vridit koordinatsystemet eller ändrat axlarna till krokiga linjer blir det
inte lika självklart att alla avstånd mellan föremål förblir oförändrade.
Vi behöver några regler som talar om vilka storheter som förblir invarianta under
koordinattransformationer.Som kan tala om att avstånd mellan föremål förblir
invarianta medan avstånd till origo inte blir det.Vi kallar storheter som uppfyller
sådana krav för tensorer.
Betrakta ett vanligt tvådimensionellt koordinatsystem med x- och y-axel.
Lägg in ett annat koordinatsystem med samma origo men med vrid det så att
axlarna bildar vinkel med det första systemets axlar.Kalla de nya axlarna
för u- och v-axel.
Ett sätt att hantera vektorer i ett koordinatsystem är att dela upp dem
i komposanter utefter axlarna.En godtycklig vektor i x-y-systemet kan alltså
delas upp i en x-komposant och en y-komposant.
Om vi vill överföra en vektor från x-y-systemet till u-v-systemet kan vi göra
så att vi delar upp den i komposanter utefter x- och y axlarna,överför dessa
komposanter till u-v-systemet och sätter ihop vektorn i u-v-systemet.
Fig 1
Om jag i stället använder laplacetransformerna överför jag integrationen till en
multiplikation med 1/s.Jag kan nu se det som att e multipliceras med G och ger
c enligt
e(s) G(s) = c(s)
Om jag öppnar kranarna till det konstanta flödet I (liter/sek) blir
e(s) = I 1/s = I/s
eftersom laplacetransformen för 1 är 1/s.
Överföringen är en integration vilket innebär att
G(s) = 1/s
vilket ger
I 1 1
c(s) = e(s) G(s) = --- --- = I ----
s s s2
Den tidsfunktion som motsvarar laplacetransformen 1/s2 är t.Vi får
alltså
c(t) = I t
Om man multiplicerar kranflödet i liter/sek med det antal sekunder man tappar får
man alltså vattenmängden.Det inser man naturligtvis direkt men det blir inte fel om
man försöker komma fram till resultatet med hjälp av laplacetransformen.Och när
e(t) och G blir mer komplicerade blir inte slutresultatet lika självklart.
Vektoranalys
============
Om man är intresserad av vindar finns det anledning att beskriva atmosfären
på sådant sätt att man kan dra slutsatser om vilka vindar som blåser, vilka
som kommer att blåsa och vilka som har blåst.
Vind är volymflöde som orsakas av tryckskillnad. Det kan alltså vara lämpligt
att beskriva atmosfären genom att ange trycket i ett antal olika punkter.
Tryck är en endimensionell vektor, d v s en skalar. Det räcker med att ange en
enda siffra för att ange trycket i en viss punkt. Denna siffra är tryck-
skillnaden mellan punkten och en absolut nollpunkt för tryck. Tryck är alltså
en potential, d v s en skalär storhet som anges som avvikelse från en nollpunkt.
Om vi beskriver atmosfären på detta sätt säger vi att den är ett potentialfält.
Om vi vet trycket p i varje punkt kan vi rita tryckkartor där vi sammanbinder
punkter med samma tryck till isobarer. På tvådimensionella kartor blir
isobarerna linjer och i tredimensionella kartor blir isobarerna ytor.
Men det är inte tryck utan tryckskillnad som driver vind. Att vi vet trycket i
en viss punkt räcker inte för att kunna säga om vinden ökar eller minskar i
punkten. Vi behöver veta hur trycket förändras i punktens omgivning.
För att beskriva tryckförändringar i punktens omgivning lägger vi in ett
treaxligt koordinatsystem med vinkelräta axlar (x , y , z) och origo i punkten.
Så går vi ett steg i x-riktningen och mäter upp tryckändringen dpx. Vi
dividerar med steglängden dx och får ett mått dpx/dx på hur snabbt trycket
ändras i x-riktningen. Så gör vi likadant i y-riktningen och i z-riktningen och
får tre siffror som anger hur snabbt trycket ändras i området runt punkten.
Vi kan alltså beskriva tryckändringen runt punkten med tre siffror d v s med en
tredimensionell vektor. Denna vektor kallas för gradient och anges med operatorn
grad. Vi kan alltså skriva
grad p = (dpx/dx dpy/dy dpz/dz)
Gradienten för en potential d v s för en skalar är alltså en vektor som anger hur
snabbt potentialen ändras i olika riktningar.
Vind är volymflöde genom ytenhet. För att mäta vinden kan vi göra en öppning med
ytan 1 m2 och se hur många m3 som passerar genom öppningen per sekund.
Sorten för vind blir då (m3/s)/m2 = m/s alltså en hastighet som vi kallar
vindhastighet. Vi betecknar vind d v s vindhastighet med v.
Vind har inte bara ett värde den har också en riktning. Den kan alltså inte som
ses som en skalär potential utan den måste behandlas som en vektor. Vi kan t ex
ange den genom att ange vind i x-riktningen (vx), vind i y-riktningen (vy) och
vind i z-riktningen (vz). Till varje punkt i atmosfären hör alltså en skalar
som anger trycket i punkten, en vektor som anger tryckändringen i punkten
och en vektor som anger vinden i punkten.
Vind i vindriktningen kallas för vindens belopp och betecknas |v|.
Vi omsluter en punkt med en sluten yta S t ex med en klotyta. Så delar vi upp
denna yta i smådelar dS som är så små att vinden kan anses vara lika i alla
delar av en sådan småyta. |v| dS cos α är då det volymflöde som strömmar ut
genom dS (α är vinkeln mellan v och normalen till dS). På en tidsenhet bortförs
alltså via dS luftvolymen |v| dS cos α från den volym som omsluts av S. Summerar
vi över alla dS får vi den luftvolym som varje tidsenhet bortförs från volymen
inom S. För att få ett mått som inte beror på hur stor volym V som S omsluter
dividerar vi med V. Vi har nu fått ett mått på hur mycket volym (observera
skillnaden mellan omsluten volym V och den flödande luftvolym v som kan
skapas) som skapas inom S och blåser ut utan att ha blåst in. Vi har alltså
fått ett mått på punkten som vindkälla. Detta anges med operatorn div som
alltså anger källstyrka.
I många fall gäller att den vind som blåser in i en punkt är lika stor som
den vind som blåser ut från punkten. Källstyrkan är då 0 och vi säger att
vinden källfri. Men om t ex solen värmer i punkten så att luftens volym ökar
kommer större volym att lämna punkten än den volym som kom in i punkten
(eftersom luft är kompressibel kommer även tryckändring att ge volymändring).
Vi får då div v > 0.
Ett flöde (t ex vind) av något (t ex luftvolym) kan alltså beskrivas som ett
vektorfält där varje punkt tilldelas en vektor (v) som anger flödets storlek i
olika riktningar. Divergensen för denna vektor (div v) anger källstyrkan för
det som flödar.
Div v, d v s källstyrkan, är en skalär storhet.
Inom ellära använder man Kirchhoffs första lag som säger att summan av alla
strömmar till en punkt är lika med summan av alla strömmar från punkten.
Kirchhoffs första lag säger alltså att strömmen är ett källfritt flöde. Vi
har alltså div I = 0 i alla punkter. Antalet laddningsbärare, d v s antalet
elektroner, som strömmar i ledningarna och utgör det flöde som är den
elektriska strömmen ändras alltså inte i någon punkt.
Maxwells ekvationer är en annan formulering av Kirchhoffs lagar och där har
Kirchhoffs första lag formen
div I = 0
Detta gäller om inte laddningsfördelningen ändras.
Vi kan ha både vind och elektrisk ström som varierar trots att källstyrkan är
noll. Men vi kan inte ha ett nettoflöde in i eller ut ur en punkt om käll-
styrkan är noll. För källor och sänkor i ett flöde är divergensen skiljd från
noll.
Små flöden kan flyta samman till ett stort och ett stort flöde kan grena sig i
många små även om källstyrkan är noll. Att källstyrkan i en punkt är större
än noll innebär att ett flöde uppstår i punkten utan att komma in i punkten
och att källstyrkan är mindre än noll innebär att ett flöde försvinner i
punkten.
Div v ≠ 0 betyder att en del av flödet v kommer från ingenstans eller
försvinner i intet. Vi kan naturligtvis säga att ett flöde kommer från eller
försvinner till en annan dimension. Om vi t ex studerar horisontella vindar
kan vi göra det i ett tvådimensionellt system med x-axeln i öst-väst och
y-axeln i nord-syd. Om vi då har div v ≠ 0 kan vi naturligtvis skriva
div v = dvz/dz och tolka det som att en del av v kommer från eller försvinner
till en tredje dimension (z). Om vi så lägger in en vertikal axel och kallar
den för z-axeln, d v s inför den tredje dimensionen som en vertikal
dimension tolkar vi vz som fallvind eller uppvind som tillför
eller bortför horisontell vind. Om detta var hela orsaken till att div v i det
tvådimensionella systemet var skiljd från noll blir div v = 0 i det
tredimensionella systemet. Skulle det dessutom finnas andra skäl,
t ex att uppvärmning ger volymutvidgning kommer div v inte att minska
ända till noll utan ha ett restvärde som vi kan tolka som kommande från
ytterligare en dimension.
Antag att vi är intresserade av en viss punkt A. Vi lägger in en plan yta
som innehåller A. Så går vi runt en sluten väg runt A i ytan. För varje steg
vi tar multiplicerar vi steglängden med vindhastigheten i stegriktningen.
Alla dessa produkter adderar vi tills vi är tillbaka till utgångspunkten. Vi
bildar alltså
S
∫ v dl
L
där
dl är steglängden och L betecknar en sluten väg
Värdet av denna integral beror på hur vi valt att lägga planet. Vi väljer så
det plan som ger maximalt värde på denna integral. Så dividerar vi med
den ytan som gångvägen omsluter och kallar det vi då får fram för beloppet
av rot v.
Om vi får lika mycket medvind som motvind när vi går runt en sluten väg är
rot v = 0. Vi säger då att vinden är virvelfri. Skulle det däremot blåsa en
virvelvind runt A kan vi följa med virveln och gå runt A så att vi hela vägen
får medvind. Vi beskriver detta med en vektor som kallas rot v som har
beloppet lika med ovanstående integral dividerad med den omslutna ytan
och riktningen sammanfallande med normalen till den omslutna ytan.
Ett exempel på ett praktiskt taget virvelfritt fält är gravitationen vid
markytan. Antag att vi går runt en sluten väg och för varje steg
multiplicerar tyngden med höjdändringen. När vi kommer tillbaka till
utgångspunkten och lägger ihop alla dessa produkter får vi det arbete
som uträttats under vägen och detta blir alltid noll hur vi än går. Det i
sin tur innebär att arbetet som uträttas när vi går från punkt A till punkt B
blir lika stort vilken väg vi än går. Vi kan då tilldela punkt A en potential
gA som motsvarar arbetet att föra en massenhet från en
referenspunkt till A. Och på motsvarande sätt kan vi tilldela punkt B en
potential gB. Arbetet att föra massan m från A till B blir
då W enligt
W = m gA - m gB = m (gA - gB)
Inom ellära använder man Kirchhoffs andra lag som säger att summan
av alla spänningar längs en sluten väg är noll, d v s att fältstyrkan är
virvelfri.
I Maxwells ekvationer har Kirchhoffs andra lag formuleringen
rot E = 0
(OBS att E här betyder elektrisk fältstyrka, inte energi)
Detta gäller om det inte finns några varierande magnetiska fält. Tids-
derivatan hos ett magnetiskt fält ger elektriska virvlar.
I ett tredimensionellt system är vi vana vid att se virvlar. Vi har alla sett
virvelvindar och virvlar när vattnet runner ur badkaret. I tre dimensioner
kan vi göra en uppdelning i ett plan och en axel vinkelrät mot planet. En
virvel runt denna axel kommer då att ligga i planet. För ett fyrdimensionellt
system tillkommer emellertid möjligheter som inte är helt lätta att före-
ställa sig. En virvel kring tidsaxeln kommer att ligga i rummet men inte
nödvändigtvis i ett plan.
Tensorkalkyl
============
Vi kan,som sagt,inte omvandla energi mellan olika former enbart genom att
flytta gränserna för de mängder vi betraktar.Världen kan inte veta hur vi
hittar på att dela upp den.
När vi lägger in koordinatsystem tilldelar vi varje punkt ett läge som anges
med ett antal koordinater.På en plan karta anger vi två koordinater,i rummet
anger vi tre koordinater och om vi tar med tiden så anger vi i rum-tiden fyra
koordinater.Vi säger att kartan är tvådimensionell,rummet tredimansionellt och
rum-tiden fyrdimensionell.Läget på en karta anges med en tvådimensionell
ortsvektor (två sammanhörande tal),i rummet med en tredimensionell ortsvektor
och i rum-tiden med en fyrdimensionell ortsvektor.
Om vi ändrar koordinatsystemet ändras ortsvektorerna.Men lika lite som världen
kan veta hur vi avgränsar våra mängder kan världen veta hur vi har hittat på
att lägga in våra koordinatsystem.Det som händer i världen måste alltså vara
oberoende av hur vi väljer att lägga in koordinatsystem.Vi säger att det finns
storheter som är invarianta under koordinattransformationer.
Lägg in ett treaxligt rätlinjigt och rätvinkligt koordinatsystem i huset.Lägg
origo vid golvet i sydvästra hörnet.Lägg x-axeln mot norr,y-axeln mot öster och
z-axeln rakt upp.Gradera axlarna i meter.Häng upp en termometer på en vägg.
Termometern får då koordinater t ex (3 , 4 , 1).
Behåll origo och z-axeln men vrid x-axel och därmed även y-axeln.Termometern får
då nya koordinater t ex (2 , 4,6 , 1).
Att vi på detta sätt ändrar koordinatsystemet skall naturligtvis inte påverka vad
termometern visar.Vi säger att temperaturen är invariant under koordinattransfor-
mationer.
Även om termometern har fått nya koordinater har den inte flyttats.Inte heller
origo har flyttats.Avståndet mellan termometern och origo måste alltså vara
oförändrat.Avstånd mellan punkter är invarianta under koordinattransformationer.
I första fallet är avståndet mellan termometern och origo 5,1 m.Om vi i andra
fallet har x = 2 och z = 1 måste alltså y ha ett värde som ger avståndet 5,1.Vi
kan då beräkna y och få det till 4,6.
Vi kan alltså inte välja nya värden på x och y hur som helst.Om vi vrider x-axeln
så att vi får en ny x-koordinat kan vi beräkna värdet på motsvarande y-koordinat.
Och har vi vridit så att vi fått nytt värde på termometerns koordinater så har
alla andra koordinater ändrats på beräkningsbart sätt.Vi kan inte fritt välja men
väl beräkna nya koordinater för stolar,bord,lampor o s v.
Vi anger termometerns läge genom att ange tre koordinater.Läget anges alltså med
tre siffror.Vi säger att termometerläget är en tredimensionell vektor.I många
läroböcker använder man pilar för att beskriva vektorer.Om vi vill tänka på denna
vektor som en pil ser vi den som en pil som startar i origo och slutar vid
termometern.Längden av denna pil kallar vi termometerns avstånd från origo.Det
blir alltså 5,1 m.
Om golvets sydvästra hörn ligger 6 m åt norr,8 m åt öster och 0,5 m över tomtens
sydvästra hörn kan vi parallellförflytta koordinatsystemet från golvets sydvästra
hörn till tomtens sysdvästra hörn.Koordinataxelriktningarna ändras då inte men
x-koordinaten ökar med 6 m,y-koordinaten ökar med 8 m och z-koordinaten ökar med
0,5 m.I stället för termometerläget (3 , 4 , 1) får vi då läget (9 , 12 , 1,5).En
sådan parallellförflyttning medför också att avståndet till origo förändras.
Parallellförflyttning av koordinatsystemet innebär alltså att termometerns avstånd
från origo ändras men däremot ändras inte avståndet mellan termometern och golvets
sydvästra hörn.Koordinaterna ändras men alla avstånd mellan verkliga punkter förblir
oförändrade.Avstånd från origo är ingen invariant storhet.Det är beroende av hur
vi väljer koordinatsystem.Avståndet mellan två fysiska föremål däremot är en
invariant storhet som måste vara oberoende av hur vi väljer koordinatsystem.
Om vi bara har gjort en parallellförflyttning d v s bara har förflyttat origo
får vi direkt att alla avstånd mellan föremål blir oförändrade.När vi drar
koordinaterna för det ena föremålet från koordinaterna för det andra försvinner
origoförflyttningen.Vi har alltså räknat bort origoförflyttningen när det blir
dags att kvadrera,addera och dra roten ur för att få fram avståndet.Men om vi
har vridit koordinatsystemet eller ändrat axlarna till krokiga linjer blir det
inte lika självklart att alla avstånd mellan föremål förblir oförändrade.
Vi behöver några regler som talar om vilka storheter som förblir invarianta under
koordinattransformationer.Som kan tala om att avstånd mellan föremål förblir
invarianta medan avstånd till origo inte blir det.Vi kallar storheter som uppfyller
sådana krav för tensorer.
Betrakta ett vanligt tvådimensionellt koordinatsystem med x- och y-axel.
Lägg in ett annat koordinatsystem med samma origo men med vrid det så att
axlarna bildar vinkel med det första systemets axlar.Kalla de nya axlarna
för u- och v-axel.
Ett sätt att hantera vektorer i ett koordinatsystem är att dela upp dem
i komposanter utefter axlarna.En godtycklig vektor i x-y-systemet kan alltså
delas upp i en x-komposant och en y-komposant.
Om vi vill överföra en vektor från x-y-systemet till u-v-systemet kan vi göra
så att vi delar upp den i komposanter utefter x- och y axlarna,överför dessa
komposanter till u-v-systemet och sätter ihop vektorn i u-v-systemet.


 Och hela vektorn i u-v-systemet blir
A = Au + Av (vektoriell addition)
Så länge vi bara sysslar med tvådimensionella koordinatsystem går det ju att
använda olika bokstäver (x , y ,u , v) för de olika axlarna.Men när man vill
studera mångdimensionella system blir det problem att benämna axlarna på detta
sätt.Inom tensoranalys använder man därför ett annat system för axelbenämning.
Inom tensoranalys ersätter man index och exponent med subscript och superscript
(jag använder de engelska benämningarna för jag har inte funnit några svenska).
x2 betyder alltså inte "x upphöjt till två" utan koordinataxel nr 2 alltså
vanligen y-axeln.I ett koordinatsystem med N axlar benämner man alltså axlarna xj
där j går från 1 till N.
Om vi kallar Ax för A1 , Ay för A2 , Au för A1 och Av för A2
kan vi skriva ovanstående uttryck för komposanter i u-v-systemet som
Och hela vektorn i u-v-systemet blir
A = Au + Av (vektoriell addition)
Så länge vi bara sysslar med tvådimensionella koordinatsystem går det ju att
använda olika bokstäver (x , y ,u , v) för de olika axlarna.Men när man vill
studera mångdimensionella system blir det problem att benämna axlarna på detta
sätt.Inom tensoranalys använder man därför ett annat system för axelbenämning.
Inom tensoranalys ersätter man index och exponent med subscript och superscript
(jag använder de engelska benämningarna för jag har inte funnit några svenska).
x2 betyder alltså inte "x upphöjt till två" utan koordinataxel nr 2 alltså
vanligen y-axeln.I ett koordinatsystem med N axlar benämner man alltså axlarna xj
där j går från 1 till N.
Om vi kallar Ax för A1 , Ay för A2 , Au för A1 och Av för A2
kan vi skriva ovanstående uttryck för komposanter i u-v-systemet som
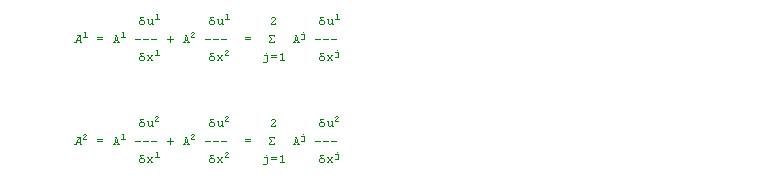 Nu närmar vi oss quintessensen av tensoranalysen.För det är nu mycket lätt att
generalisera denna transformation till att gälla för hur många dimensioner som helst.
En transformation från ett x-system med N dimensioner till ett u-system med N
dimensioner gör man tydligen så att u-systemets komposanter blir
Nu närmar vi oss quintessensen av tensoranalysen.För det är nu mycket lätt att
generalisera denna transformation till att gälla för hur många dimensioner som helst.
En transformation från ett x-system med N dimensioner till ett u-system med N
dimensioner gör man tydligen så att u-systemets komposanter blir
 Genom att låta p gå från 1 till N får man då alla N komposanterna i u-systemet och
kan addera dem (vektoriellt) till den transformerade vektorn.
Att man kan skriva som efter sista likhetstecknet i uttrycket ovan beror på att man
inom tensoranalys använder en regel som säger att om samma superscript eller subscript
förekommer två gånger i samma term så skall man summera för alla värden på detta från
1 till N (summakonventionen).Eftersom j förekommer på två ställen skall man alltså
summera för j=1 till N.
Om en storhet transformeras enligt denna ekvation kallas den en tensor.
j förekommer här i nämnaren på differentialuttrycket.En tensor där summationsscriptet
förekommer i nämnaren på differentialuttrycket kallas contravariant.Om det finns i
täljaren kallas tensorn covariant.Man använder superscript för att ange element
av en contravariant tensor och subscript för att ange element av en covariant
tensor.Hanteringen av superscript och subscript är en viktig del av tensoranalysen.
Många operationer med tensorer kan göras enbart genom att man använder räkneregler
som gäller för tensorernas superscript och subscript.
Enkla siffervärden (skalarer) som temperatur transformeras direkt mellan koordinat-
system utan att några komposanter ändras.Sådana värden kallas för tensorer av nollte
ordningen.Vanliga vektorer får nya axelkomposanter när de transformeras till nya
koordinatsystem.De kallas för tensorer av första ordningen.
Exempel på tensorer av första ordningen är hastighet (definierad som lägesförändring
per parametertid) och avstånd mellan föremål.
I den gröna texten har jag försökt beskriva hur man kommer fram till vad en
tensor är.Jag har där bara sett på vridning av koordinatsystem med räta linjer
som axlar men en poäng med tensoranalysen är att den gäller även för andra typer
av koordinatsystem.Vi kan ha cylindriska eller sfäriska system eller system med
krokiga axlar t ex hyperbler.
Och den kanske viktigaste användningen har varit inom relativitetsteori eftersom
den medger att man arbetar med fyra (eller fler) dimensioner.De regler som gäller
för hantering av tensorer går alltså att använda när man försöker ställa upp
samband i den fyrdimensionella rum-tiden.
Genom att låta p gå från 1 till N får man då alla N komposanterna i u-systemet och
kan addera dem (vektoriellt) till den transformerade vektorn.
Att man kan skriva som efter sista likhetstecknet i uttrycket ovan beror på att man
inom tensoranalys använder en regel som säger att om samma superscript eller subscript
förekommer två gånger i samma term så skall man summera för alla värden på detta från
1 till N (summakonventionen).Eftersom j förekommer på två ställen skall man alltså
summera för j=1 till N.
Om en storhet transformeras enligt denna ekvation kallas den en tensor.
j förekommer här i nämnaren på differentialuttrycket.En tensor där summationsscriptet
förekommer i nämnaren på differentialuttrycket kallas contravariant.Om det finns i
täljaren kallas tensorn covariant.Man använder superscript för att ange element
av en contravariant tensor och subscript för att ange element av en covariant
tensor.Hanteringen av superscript och subscript är en viktig del av tensoranalysen.
Många operationer med tensorer kan göras enbart genom att man använder räkneregler
som gäller för tensorernas superscript och subscript.
Enkla siffervärden (skalarer) som temperatur transformeras direkt mellan koordinat-
system utan att några komposanter ändras.Sådana värden kallas för tensorer av nollte
ordningen.Vanliga vektorer får nya axelkomposanter när de transformeras till nya
koordinatsystem.De kallas för tensorer av första ordningen.
Exempel på tensorer av första ordningen är hastighet (definierad som lägesförändring
per parametertid) och avstånd mellan föremål.
I den gröna texten har jag försökt beskriva hur man kommer fram till vad en
tensor är.Jag har där bara sett på vridning av koordinatsystem med räta linjer
som axlar men en poäng med tensoranalysen är att den gäller även för andra typer
av koordinatsystem.Vi kan ha cylindriska eller sfäriska system eller system med
krokiga axlar t ex hyperbler.
Och den kanske viktigaste användningen har varit inom relativitetsteori eftersom
den medger att man arbetar med fyra (eller fler) dimensioner.De regler som gäller
för hantering av tensorer går alltså att använda när man försöker ställa upp
samband i den fyrdimensionella rum-tiden.
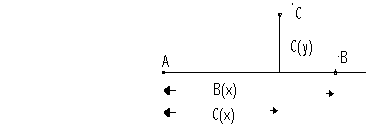 Fig 1
I fig 1 har punkten A koordinaterna 0,0 (om jag lägger origo i A).
Punkten B har koordinaterna B(x),0 och punkten C har koordinaterna
C(x),C(y).
En tvådimensionell värld kallar vi för en yta.
Om vi nu utökar vår värld med en fjärde punkt D kan denna falla i ytan
men det är också möjligt att den hamnar utanför ytan. Om den hamnar utanför
ytan anger vi dess läge genom att ange de två koordinaterna för punktens
projektion på ytan plus en tredje koordinat som anger avståndet till ytan.
För att ange läge i denna värld krävs alltså att man anger tre koordinater
och vi kallar en sådan värld tredimensionell.
Tre koordinater kan vi projicera på tre vinkelräta räta linjer som vi
kallar för koordinataxlar. Ett sådant koordinatsystem kallas för
cartesianskt.Det finns andra sätt att åstadkoma koordinatsystem. Man kan
t ex ange en sträcka och två vinklar eller använda system med krökta
koordinataxlar men tills vidare får det cartesianska systemet räcka.
Vad händer när vi lägger till en femte punkt E?Hittills har det för varje
ny punkt varit möjligt att lägga den utanför den etablerade världen så att
den gett en ny dimension. Gäller detta även för punkt E?
Vår hjärna har ett program som inte kan räkna med mer än tre vinkelräta
rätlinjiga axlar. Men betyder det att det inte kan finnas fler eller
betyder det bara att vi ser världen projicerad på ett treaxligt
koordinatsystem? Hur skall vi veta om det räcker med tre axlar?
Vi behöver ett kriterium som vi kan använda för att avgöra om ett
koordinatsystem är fullständigt eller inte.Ett sådant kriterium skulle
kunna formuleras på följande sätt:
Om två partiklar kan ha samtliga koordinater lika utan att de
växelverkar är koordinatsystemet ofullständigt.
Det är uppenbart att ett tredimensionellt koordinatsystem är
ofullständigt. Två bilar kan köra genom en korsning så att de i alla
avseenden har samma lägeskoordinater men om de gör det vid olika tidpunkt
finns ingen växelverkan mellan dem. Lägger vi då till tid som en fjärde
koordinataxel finner vi att om alla fyra koordinaterna sammanfaller
för bilarna får vi alltid en mycket påtaglig växelverkan mellan dem.
Ett koordinatsystem som beskriver en fyrdimensionell värld förefaller vara
fullständigt.
Man skulle kunna diskutera om t ex frekvens skulle kunna ses som en femte
dimension. Två signaler med olika frekvens kan ju samtidigt finnas på
samma antenn utan att störa varandra. Men detta beror på att etern och
antennen är praktiskt taget linjära så att summan av signalerna inte
innehåller något annat än det som fanns i de båda signalerna. Ersätter
vi antennen med ett olinjärt element, t ex en diod, ger växelverkan mellan
signalerna upphov till en ny signal som inte fanns i de ingående
signalerna. Vi behöver alltså ett olinjärt element för att se växelverkan
men att den inte syns med en linjär antenn motiverar inte att vi ser
frekvens som en femte dimension.
I princip kan varje ny punkt som avviker från omgivningen dyka upp i en
ny dimension. Antalet möjliga dimensioner är alltså antalet partiklar
minus ett. Att vår värld med alla dess partiklar ryms inom fyra dimensioner
eller åtminstone med framgång kan projiceras på fyra dimensioner, är ett av
de stora mysterierna.
Det påstås ibland att världen vid Big Bang skulle ha haft elva dimensioner
men jag har aldrig hittat någon vettig motivering för detta påstående
och jag betraktar därför detta, liksom hela Big Bang-iden, tills vidare som
Hokus Pokus eller snarare som Hoc est...
Vad är energi?
==============
Sedan urminnes tid har människan försökt förändra sin omgivning för att få
den att stämma med hennes önskemål. Sådan förändring kräver ansträngning och
vi kallar detta för arbete.
Förändring av omgivningen är i många fall det samma som att flytta föremål.
Om alla koordinater för alla partiklar är oförändrade har ju ingenting
ändrats. En förändring innebär alltså att några koordinater måste ändras
d v s att något måste förflyttas. Om vi vill flytta ett föremål trots att
det av någon anledning tar emot måste vi anstränga oss, d v s vi måste
uträtta ett arbete. I tekniska sammanhang studerar man endast denna typ
av arbete och för att skilja detta från andra former av arbete, t ex från
tankearbete, använder vi benämningen tekniskt arbete eller om det inte
finns risk för missförstånd enbart begreppet arbete.
Den ansträngning som krävs för att flytta ett föremål beror dels på hur
mycket man måste ta i för att rubba föremålet d v s på den kraft som
erfordras dels på hur långt man flyttar det. Vi säger att arbete är
produkten av kraft gånger väg.
För några hundra år sedan började man förstå att det fanns andra sätt
att åstadkomma arbete än via muskelarbete. Man använde t ex vind och
forsar. Så småningom lärde vi oss också att använda temperaturändringar
för att få gaser att ändra volym och därmed uträtta arbete.
Vi fann att alla förutsebara förändringar kunde omvandlas till nyttigt
arbete. Ju mer vi lärde oss om att omvandla olika förändringar till
arbete ju större blev behovet av ett begrepp och av måttenheter för
allt som kunde omvandlas till arbete. Vi började kalla allt som kunde
omvandlas till arbete för "energi".
Om vi har ett tillstånd som på något sätt avviker från det mest sannolika
kan vi förutse att detta kommer att förändras så att det närmar sig det
mest sannolika. En sådan avvikelse är alltså en potentiell förändring
d v s energi.
Att en förändring är förutsägbar innebär att vi kan beräkna dess storlek.
Men för sådana beräkningar behöver vi kvantitativa mått. Vi brukar då se
energi som en produkt av två mätbara storheter. Ofta gör vi den
uppdelningen så att den ena storheten kan betraktas som en mängdstorhet
(extensiv faktor) och den andra som en intensitetsfaktor (intensiv
faktor).
Energi är alltså ett kvantitativt mått på förutsägbar förändring.
Antag att en kula ligger på ett bord. Om kulan rullar över bordskanten
inträffar en förutsägbar förändring, kulan faller från bordet mot golvet.
Ju högre bordet är ju större är denna förutsägbara förändring och ju
tyngre kulan är ju större är förändringen. Vi säger att bordets höjd
gånger kulans tyngd är den förutsägbara förändringen som inträffar när
kulan faller från bordet, d v s bordets höjd gånger kulans tyngd är kulans
energi.
När vi talar om energianvändning menar vi att vi använder spontana förutsäg-
bara förändringar för att åstadkomma de förändringar vi önskar. Begreppet
"förutsägbarhet" är nära knutet till begreppet "användbarhet". Vill vi t ex
klyva ett vedträ försöker vi åstadkomma en situation där vi kan förutse att
vi får en förändring som resulterar i att vedträt klyvs. Vi sätter oss inte
och väntar på att slumpmässiga förändringar skall leda till att vedträt
spricker.
Med energikällor menar vi tillstånd som avviker från omgivningen på sådant sätt
att vi kan förutse att dessa avvikelser kommer att utjämnas.
Låt oss se på några exempel på avvikelser som vi anser användbara och avvikelser
som skulle kunna vara användbara.
Betrakta en avgränsad gasmängd, t ex en luftmassa. Låt oss först se på
molekylernas läge. Om medelvärdet av molekylernas avstånd till varandra
avviker från motsvarande medelvärde i omgivningen har vi en täthets-
avvikelse mellan gasmängden och omgivningen. Vi kan förutsäga att om
vi möjliggör utbyte med omgivningen kommer denna täthetsavvikelse att
utjämnas. Denna utjämning blir en förutsägbar förändring. Avvikelse i
medelavstånd betraktar vi som användbar energi.
Om molekylavståndets varians avviker från omgivningens kan vi förutsäga
att denna avvikelse kommer att utjämnas. Avvikelser i molekylavståndets
varians är alltså i princip användbara men vi känner ingen metod att
utnyttja dessa och betraktar dem därför inte som användbar energi.
Låt oss så se på tidsderivatan av läget, d v s på molekylhastigheten.
Om medelvärdet av molekylhastigheten avviker från motsvarande hastighet
i omgivningen har vi en vind som vi kan utnyttja. Vi kan t ex låta
hastighetsskillnaden utjämnas via en propeller på en vindsnurra. Utjämning
av skillnad i molekylernas medelhastighet betraktar vi alltså som
användbar energi.
Om molekylhastighetens varians avviker från motsvarande storhet i
omgivningen säger vi att vi har en temperaturavvikelse mot omgivningen.
Temperatur är ju molekylvikt gånger molekylhastighetens varians. På
1800-talet lärde vi oss att använda förutsägbara förändringar av
molekylhastighetens varians, d v s vi lärde oss att omvandla värme i
andra energiformer.
Avvikelser i medelvärde och varians för andra tidsderivatan av läget
borde också vara användbara. D v s avvikelser i medelvärde och varians
för molekylaccelerationen borde vara användbara. Men för andra tids-
derivatan har vi, lika lite som för högre derivator, någon praktisk
metod för energiomvandling.
Det är också så att ett tillstånd kan avvika från omgivningen på andra
sätt än de som karaktäriseras av medelvärde och varians. Det är inte
svårt att tänka sig osannolika fördelningar med samma medelvärde och
varians som omgivningen. Om en fördelning är osannolik kan vi förutsäga
att den spontant kommer att övergå till en mera sannolik. En sådan
fördelning är alltså användbar eftersom den ger en förutsägbar
förändring. Men frånsett ett fåtal osannolika tillstånd med avvikande
medelvärde och varians känner vi inte till praktiska metoder att
använda de osannolika tillstånd som omger oss. Och vi gör knappast
några försök att finna sådana metoder.
När vi pratar om energi brukar vi utgå från att vi skall använda
osannolikt stora avvikelser från medelvärde eller varians. Men för
ett tillstånd där avvikelserna är osannolikt små kan vi också förutsäga
hur tillståndet kommer att förändras. Här finns alltså en hel klass
"användbara" (i betydelsen förutsägbart föränderliga) tillstånd som
är lika stor som den dit alla våra kända energikällor hör men där vi
idag inte har någon aning om de kan användas praktiskt och i så fall
hur och till vad.
Att man kunde använda avvikelser i luftmolekylernas medelhastighet, d v s
vind, var känt sedan urminnes tid. Att segla med hjälp av vind är en
gammal konst. Att man även kan använda avvikelser i varians för luft-
molekylernas hastighet, d v s temperaturskillnader, för att driva maskiner
är en kunskap som bara är några få århundraden gammal. Det är naturligtvis
fullt tänkbart att vi om något århundrade betraktar användning av
avvikelser hos högre tidsderivator eller i fördelningsmått av högre
ordning som lika självklart som vi idag ser användning av värmemaskiner.
Att värme från brinnande olja skulle kunna driva en bil måste för 1700-
talets människor ha tett sig som helt otänkbart. Men trots det fanns det
de som försökte och gjorde detta möjligt att uppnå så småningom.
Vad är tid ?
============
Energi är förutsebara förändringar som vi genom förutsebarheten kan
utnyttja och omvandla enligt våra önskemål. Men vi behöver också ett
begrepp för och ett mått på alla förändringar som påverkar vår omgivning.
Summan av alla förändringar kallar vi tid.
Energi och tid är alltså mycket nära besläktade begrepp.Båda är
kvantitativa förändringsmått.
När vi använder energi använder vi en del av den förutsägbara delen av
de förändringar som utgör tidsflödet.
Varje märkbar förändring är en händelse och varje händelse är ett
tidsinkrement. I princip skulle vi kunna mäta tid i antal tidsinkrement
men det skulle bli ohanterligt stora tal för praktiskt bruk och vi brukar
därför använda enheten sekund som är ett visst (stort) antal tidsinkrement
eller år som är ännu fler tidsinkrement.
Händelser inträffar slumpvis men händelser kan vara kopplade så att
händelse A kan öka sannolikheten för händelse B.Om man kör en bil innebär
händelsen att framänden rör sig i förhållande till vägen att sannolikheten
för händelsen att bakänden skall röra sig i förhållande till vägen ökar.
Och det finns en kedja av kopplade händelser som via gasspjället,
förbränning i motorn och vridning av drivhjulen höjer sannolikheten att
bilen skall röra sig på vägen.
Ett sätt att beskriva tidsflödet kan vara att likna det vid lotterier.
Antag att man har 106 lotterier med vardera 106 lotter.
Varje lott motsvarar en potentiell händelse och varje vinst motsvarar att
händelsen inträffar. Om varje lotteri har 100 vinster är sannolikheten
att vinna i en dragning om man vet att man har en lott i rätt lotteri
1/104. Om man inte vet vilket lotteri man har en lott i blir sannolikheten
för vinst 1/1010. Koppling av händelser motsvaras av koppling av lotter
genom att de tillhör samma lotteri.
Om jag köper 103 lotter blir sannolikheten för vinst i varje dragning
1/107. När jag har fått 10 vinster kan jag alltså dra slutsatsen att det
har förekommit 108 dragningar vilket innebär att 1010 vinster
har fallit ut. Genom att följa vinstutfallet på min lilla lottbunt kan jag alltså
dra slutsatser om totala vinstutfallet i alla lotterier.
På motsvarande sätt kan vi avgränsa en grupp potentiella händelser och
genom att se hur många av dem som inträffar kan vi dra slutsatser om hur
många händelser som inträffar i hela universum. Vi kan t ex avgränsa en
svängande pendel, en oro, en kvartskristall eller en grupp cesiumatomer.
Kring detta avgränsade system kan vi bygga en klocka som mäter totala
antalet händelser i universum.
Det antal händelser som klockan mäter är en viss fast andel av totala
antalet händelser. För att få totala antalet händelser skall vi alltså
multiplicera det antal som klockan mätt upp med en konstant. Storleken
på denna konstant vet vi inte. Vi vet bara att det är en konstant.
Vi kan alltså inte fastställa konstantens värde men vi kan övertyga oss
om att det verkligen är fråga om en konstant.
Om våra klockor verkligen mäter totala antalet händelser i universum
skall alla klockor ange samma värde. Det är svårt att veta hur vi har
avgränsat våra klockor d v s att veta hur många lotter vi har köpt men
om de kan gå utan koppling till ovidkommande händelser skall det vara
möjligt att sätta på dem urverk med sådan utväxling att de går lika
fort. Och har vi en gång fått dem att gå lika fort skall de fortsätta
att göra det.
Vi finner då, mycket riktigt, att ju bättre vi kan avgränsa våra klockor
från koppling till ovidkommande händelser ju bättre går de. En svängande
pendel påverkas av vibrationer i upphängningen, temperaturvariationer,
luftrörelser mm. Men trots det visar olika pendelur påtaglig
överensstämmelse.
För en grupp cesiumatomer är möjligheten att undvika inverkan av
ovidkommande händelser betydligt bättre än för en pendel. Det är också
möjligt att bygga atomur som visar mycket god överensstämmelse.
Vad vill vi egentligen?
=======================
Teknik är att,via någon form av utväxling,anpassa extensiv och intensiv
faktor till vad vi har tillgång till.Till exempel att via ett spett
åstadkomma ökad kraft för att rubba en sten.
Teknik är också att utnyttja förutsägbara förändringar i vår omgivning till
att motsvara våra önskemål.Till exempel att använda den förutsägbara
förändringen när ett vedträ brinner genom att ta in det och tända det i
spisen när det är kallt i rummet.
Och teknik är också att analysera våra önskemål så att vi slipper anstränga
oss för sådant som vi inte är intresserade av.
Om Gustav III hade bestämt sig för att satsa på att kunna meddela sig
snabbare med Göteborg hade man hamnat i att bygga bättre vägar, att bygga
gästgivargårdar utefter vägarna och att avla fram bättre hästar. Vi hade
fått kurirer som på löddriga springare sprängde fram genom landet med brev
i postväskan.
När järnvägen kom fick vi, på köpet, snabbare brevbefordran.
Men den stora förändringen kom när man insåg att det handlade om att
överföra brevets innehåll, inte själva brevet. I vissa länder byggde man
optiska telegrafer där man från torn till torn överförde signaler genom
att en operatör i ett torn kunde se hur operatören i föregående torn
ställde sina signalskivor och så upprepa dessa inställningar i sitt torn
så att de kunde ses från nästa torn.
Vi ser den optiska telegrafen som ett monster av personalkrävande
ineffektivitet men när alternativet var kurirer ute på vägarna innebar
den en enorm besparing både av arbetskraft och överföringstid.
Med en elektrisk ledning mellan tornen kunde man signalera med större
tornavstånd. Och genom att man insåg att varje meddelande kan brytas ner
i binära bitar kunde man med morse-kod signalera via en enda tråd (eller
ett trådpar).
Genom att analysera vad vi egentligen önskade har vi alltså insett att
brevet inte var nödvändigt och att budskapet kunde reduceras till binära
bitar. Det har fört oss långt bort från hästavel och medfört att vi idag
tar för givet att överföringstid mellan Stockholm och Göteborg räknas i
millisekunder, inte i dagar.
När jag var liten, i mitten av 1900-talet, var det fortfarande vanligt
att man på vintrarna sågade upp is på sjöarna. Isblocken körde man hem
och lade i sågspånshögar så att man hade tillgång till is under sommaren.
I städerna använde man isskåp där maten hölls sval av is som man köpte av
en iskarl som åkte runt och sålde is. Många iskarlar trodde nog att de
faktiskt sålde is men en närmare analys av problemet ledde till insikten
att de sålde kyla och därmed till frågan om vilka möjligheter det fanns
att åstadkomma kyla. Och resultatet av den insikten blev Electroluxkylskåpet
och kompressorkylskåpet.
När man började bygga drivande och drivna maskiner behövde man göra en
uppdelning så att de som arbetade med att utveckla drivande maskiner kunde
arbeta utan att nödvändigtvis veta vad maskinen skulle driva och att de som
utvecklade drivna maskiner kunde arbeta utan att vara låsta till en viss
drivmaskin. Detta löste man med den roterande axeln som standardiserat
kopplingselement. En drivande maskin skulle alltid avslutas med en roterande
axel och en driven maskin skulle alltid försörjas via en roterande axel.
Sedan dess har elektrisk kraftöverföring utvecklats från att vara ett
alternativ för överföringar på några kilometer till att bli konkurenskraftig
på allt kortare överföringar. Möjligheten att styra strömmar med
halvledarteknik har idag medfört att elektrisk kraftöverföring mycket
ofta är konkurenskraftig även på de korta avstånd som den roterande axeln
använts för. Ett exempel som just nu är aktuellt är att ersätta
kardanaxelöverföringen i bilar med elektrisk kraftöverföring.
Insikten att den roterande axeln kan ersättas med andra kopplingselement,
t ex elektrisk, pneumatisk eller hydraulisk överföring, kommer att öppna
många av de låsningar som den roterande axeln medfört, t ex begränsningar
i rörelsemönster hos en kolv med vevstake och sinusformens dominerande
ställning inom elteknik.
Som exempel på undermålig teknik i dagens samhälle kan man nämna att vi
flyttar drygt ett ton bil för att flytta 80 kg människa och än värre att
vi inom kollektivtrafiken ofta flyttar tomma bussar på tiotals ton utan
att uträtta något önskat transportarbete över huvud taget.
Ett annat exempel är framdrivning av båtar. Vi utgår då från en fram- och
återgående kolv. Denna kolvrörelse omvandlar vi via ett vevparti till
rotation. Rotationen överför vi till en propeller som åstadkommer vatten-
rotation och framdrivning. För tändning och för försörjning av hjälpsystem
har vi också vanligtvis någon typ av elgenerator. En gång i tiden motiverades
övergången till rotation av att man använde svänghjul för att driva motorns
ickedrivande takter. Men med dagens magnetmaterial och halvledarteknik kan
man åstadkomma detta med elektrisk drivning vilket skulle innebära att man
slipper hela vevpartiet, alla problem med propelleraxelgenomföringar och alla
förluster i form av vattenrotation. Man kan i stället låta den fram- och
återgående kolven verka direkt mot vattnet.
De första och viktigaste frågorna som man alltid måste ställa sig vid
teknisk utveckling är alltså "Vad är önskat resultat?" och "Finns det
något enklare sätt att uppnå detta?".
Det finns en vandringssägen om hur man inom NASA drev ett projekt med
syfte att ta fram en lättare rakapparat som astronauterna skulle kunna
ha vid längre resor. Projektet pågick tills en av teknikerna gick ner
till butiken på hörnet och köpte en rakhyvel.
Hastighet
=========
Jag träffade en gång i tiden en pedagog som sa:
"När eleverna kommer till skolan vet de mycket väl vad hastighet är. Så
inför vi begreppet hastighet som kvoten mellan väg och tid och efter det
begriper de ingenting."
För att krångla till det ytterligare skulle jag vilja påstå att hastighet
är ett mått på hur stor andel av totala antalet händelser i universum som
flyttar en av de punkter som jag för tillfället är intresserad av i en viss
riktning.
Och så gäller det att reda ut det på ett begripligt sätt.
Betrakta en bil som kör på en väg. Lägg in ett koordinatsystem på sådant
sätt att lägeskoordinaterna för punkter i vägen förblir i stort sett
konstanta. När bilen fått upp farten kommer lägeskoordinaterna för en
partikel i bilen att ändras. Och denna partikel är kopplad till övriga
partiklar i bilen på sådant sätt att sannolikheten är stor att även
dessas koordinater skall ändras på liknande sätt.
Och varje gång en händelse inträffar i universum ökar tiden ett tids-
inkrement.
Om vi läser av lägeskoordinaterna för en partikel i bilen,väntar tills
tiden ökat med ett visst antal händelser (t ex en sekund) och därefter
på nytt läser av lägeskoordinaterna för partikeln får vi alltså veta hur
mycket partikelns läge ändrats under det att ett visst antal händelser
inträffat i universum. Men minsta detekterbara lägesförändring är en
händelse och att vi får veta hur mycket läget ändrats betyder alltså
att vi får veta hur många detekterbara lägesförändringar i rörelse-
riktningen partikeln gjort d v s hur många av alla händelser som inträffat
i universum som avsåg förflyttning av vår partikel i rörelseriktningen.
Om vi dividerar detta antal händelser med totala antalet händelser d v s
om vi dividerar lägesändringen för vår partikel med den tid som läges-
förändringen tagit får vi det som vi brukar kalla hastighet.
Vad jag gör när jag trampar ner gaspedalen i bilen är alltså att jag
försöker få en större andel av alla de händelser som inträffar i
universum att handla om att bilens läge på vägen ändras.
Om bilen flyttar sig sträckan s på tiden τ blir hastigheten v där
v = s/τ
Men om jag trampar på gasen ökar hastigheten. Om jag beräknar hastigheten
som s/τ får jag medelvärdet av hastigheten under tiden τ. Ibland är det vad
jag vill ha men ibland är jag mer intresserad av att veta hur stor
hastighet jag uppnått vid slutet av tiden τ (eller av något annat).
Hur beräknar man hastighet när den inte är konstant under mättiden?
Låt oss börja med att se på det enkla fallet att hastigheten är
proportionell mot tiden.Vi kan då skriva
v = a τ
där proportionalitetskonstanten a kallas för accelerationen.
Hur långt kommer ett föremål som från hastigheten noll accelererar med
accelerationen a under tiden τ?
Efter tiden τ är hastigheten v = a τ men medelhastigheten under tiden τ
blir hälften så stor d v s
v = a τ/2
medel
och sträckan s som föremålet tillryggalägger blir
s = v τ = a τ2 /2
medel
Men varför är det intressant att se på fallet med konstant acceleration?
Är det bara för att det är lätt att räkna på eller är det för att sådant
förekommer i verkligheten?
Om man påverkar ett föremål med konstant kraft får man faktiskt (bortsett
från luftmotstånd,friktion o dyl) konstant acceleration. Kraften F på ett
föremål med massan m ger accelerationen a enligt
F = m a
Och ett vanligt fall där man har konstant kraft är vid fallrörelser. Jordens
dragningskraft påverkar ett föremål vid jordytan med en kraft som är
praktiskt taget proportionell mot föremålets massa. När vi släpper ett
föremål och låter det falla fritt blir alltså accelerationen alltid densamma.
Vi får för fritt fall
a = 9,81 m/s2
För denna acceleration används ofta symbolen g.
Parametertid och koordinattid
=============================
Vi tänker oss en observatör som bara kan tänka i två dimensioner. Han ser
alltså världen projicerad på en yta på samma sätt som vi ser den med ett
öga eller när vi avbildar den med en kamera.
Om någon partikel ändrar höjd över denna yta förändras världen men det är
inte säkert att det märks i hans projektion. Indirekt kan han upptäcka
förändringen t ex genom att han flyttar sig så att partikelprojektionen
ändras. Han kan alltså ana sig till att hans bild är ofullständig och att
han bör ange denna typ av förändring genom att lägga till en tredje
koordinataxel.
På liknande sätt kan vi ana oss till att vi bör lägga till en tidsaxel
till vårt treaxliga rumssystem.
Om vi befinner oss i ett slutet rum,som vi kan kalla vårt observationsrum,
kan vi göra tankeexperimentet att vi bestämmer koordinaterna för alla
partiklar i rummet. Om vi så gör om bestämningen och finner att samtliga
koordinater är oförändrade är då allt oförändrat?
Nej det kan vi inte påstå för det kan ju ha inträffat händelser som förändrat
rummet i sin helhet i förhållande till världen i övrigt. För att ange det
behöver vi någon koordinataxel där vi kan avsätta observationsrummets läge
i förhållande till världen i övrigt. Vi kan kalla denna koordinat för
koordinattid.
Vi får då två tidsbegrepp som vi kan kalla
Parametertid
Koordinattid
Parametertid anger antalet händelser i universum oavsett var de inträffat.
Så snart någon partikel i universum ändrar läge så mycket att det är
detekterbart går alltså parametertiden ett tidsinkrement.
Koordinattiden går ett tidsinkrement varje gång en detekterbar händelse
inträffar utanför observationsrummet. En händelse som inträffar i
observationsrummet innebär att någon eller några rumskoordinater ändras
i observationsrummet. En händelse som inträffar utanför observationsrummet
innebär att koordinattiden ökar.
Antag att vi betraktar uppskjutning av en bemannad raket. Vi kan då lägga
x-axeln i raketens färdriktnig och strunta i y- och z-axlarna. Vi kan då
beskriva vad som händer i ett tvåaxligt koordinatsystem med en rumsaxel
(x-axeln) och en tidsaxel (koordinattid).
För oss är raketen en del av observationsrummet som ändrar läge i förhållande
till resten av observationsrummet. För besättningen ombord på raketen däremot
är raketens kontrollrum observationsrummet där,i stort sett allt står stilla.
Vi har lagt vår x-axel och vår axel för koordinattid så att huvuddelen av
vår omgivning har konstant x-koordinat medan raketens x-koordinat ökar.
Besättningen på raketen däremot lägger sin x-axel och sin axel för
koordinattid så att det mesta i raketen har konstant x-koordinat.
När raketen startar accelererar den men låt oss göra tankeexperinmentet att
den slår av motorn efter en stund och går med konstant hastighet. Dess bana
i vårt tvåaxliga koordinatsystem blir då en rät linje. Och besättningen på
raketen lägger sin axel för koordinattid längs denna räta linje. Raketens
hastighet innebär alltså att besättningens koordinatsystem vrids vinkeln
α i förhållande till vårt koordinatsystem. Och om vi mäter längd och
tid i samma enhet (t ex både längd och tid i meter eller både längd och tid
i sekunder) blir raketens hastighet sin α om vi använder parametertid
eller tan α om vi använder koordinattid.
Fig 1
I fig 1 har punkten A koordinaterna 0,0 (om jag lägger origo i A).
Punkten B har koordinaterna B(x),0 och punkten C har koordinaterna
C(x),C(y).
En tvådimensionell värld kallar vi för en yta.
Om vi nu utökar vår värld med en fjärde punkt D kan denna falla i ytan
men det är också möjligt att den hamnar utanför ytan. Om den hamnar utanför
ytan anger vi dess läge genom att ange de två koordinaterna för punktens
projektion på ytan plus en tredje koordinat som anger avståndet till ytan.
För att ange läge i denna värld krävs alltså att man anger tre koordinater
och vi kallar en sådan värld tredimensionell.
Tre koordinater kan vi projicera på tre vinkelräta räta linjer som vi
kallar för koordinataxlar. Ett sådant koordinatsystem kallas för
cartesianskt.Det finns andra sätt att åstadkoma koordinatsystem. Man kan
t ex ange en sträcka och två vinklar eller använda system med krökta
koordinataxlar men tills vidare får det cartesianska systemet räcka.
Vad händer när vi lägger till en femte punkt E?Hittills har det för varje
ny punkt varit möjligt att lägga den utanför den etablerade världen så att
den gett en ny dimension. Gäller detta även för punkt E?
Vår hjärna har ett program som inte kan räkna med mer än tre vinkelräta
rätlinjiga axlar. Men betyder det att det inte kan finnas fler eller
betyder det bara att vi ser världen projicerad på ett treaxligt
koordinatsystem? Hur skall vi veta om det räcker med tre axlar?
Vi behöver ett kriterium som vi kan använda för att avgöra om ett
koordinatsystem är fullständigt eller inte.Ett sådant kriterium skulle
kunna formuleras på följande sätt:
Om två partiklar kan ha samtliga koordinater lika utan att de
växelverkar är koordinatsystemet ofullständigt.
Det är uppenbart att ett tredimensionellt koordinatsystem är
ofullständigt. Två bilar kan köra genom en korsning så att de i alla
avseenden har samma lägeskoordinater men om de gör det vid olika tidpunkt
finns ingen växelverkan mellan dem. Lägger vi då till tid som en fjärde
koordinataxel finner vi att om alla fyra koordinaterna sammanfaller
för bilarna får vi alltid en mycket påtaglig växelverkan mellan dem.
Ett koordinatsystem som beskriver en fyrdimensionell värld förefaller vara
fullständigt.
Man skulle kunna diskutera om t ex frekvens skulle kunna ses som en femte
dimension. Två signaler med olika frekvens kan ju samtidigt finnas på
samma antenn utan att störa varandra. Men detta beror på att etern och
antennen är praktiskt taget linjära så att summan av signalerna inte
innehåller något annat än det som fanns i de båda signalerna. Ersätter
vi antennen med ett olinjärt element, t ex en diod, ger växelverkan mellan
signalerna upphov till en ny signal som inte fanns i de ingående
signalerna. Vi behöver alltså ett olinjärt element för att se växelverkan
men att den inte syns med en linjär antenn motiverar inte att vi ser
frekvens som en femte dimension.
I princip kan varje ny punkt som avviker från omgivningen dyka upp i en
ny dimension. Antalet möjliga dimensioner är alltså antalet partiklar
minus ett. Att vår värld med alla dess partiklar ryms inom fyra dimensioner
eller åtminstone med framgång kan projiceras på fyra dimensioner, är ett av
de stora mysterierna.
Det påstås ibland att världen vid Big Bang skulle ha haft elva dimensioner
men jag har aldrig hittat någon vettig motivering för detta påstående
och jag betraktar därför detta, liksom hela Big Bang-iden, tills vidare som
Hokus Pokus eller snarare som Hoc est...
Vad är energi?
==============
Sedan urminnes tid har människan försökt förändra sin omgivning för att få
den att stämma med hennes önskemål. Sådan förändring kräver ansträngning och
vi kallar detta för arbete.
Förändring av omgivningen är i många fall det samma som att flytta föremål.
Om alla koordinater för alla partiklar är oförändrade har ju ingenting
ändrats. En förändring innebär alltså att några koordinater måste ändras
d v s att något måste förflyttas. Om vi vill flytta ett föremål trots att
det av någon anledning tar emot måste vi anstränga oss, d v s vi måste
uträtta ett arbete. I tekniska sammanhang studerar man endast denna typ
av arbete och för att skilja detta från andra former av arbete, t ex från
tankearbete, använder vi benämningen tekniskt arbete eller om det inte
finns risk för missförstånd enbart begreppet arbete.
Den ansträngning som krävs för att flytta ett föremål beror dels på hur
mycket man måste ta i för att rubba föremålet d v s på den kraft som
erfordras dels på hur långt man flyttar det. Vi säger att arbete är
produkten av kraft gånger väg.
För några hundra år sedan började man förstå att det fanns andra sätt
att åstadkomma arbete än via muskelarbete. Man använde t ex vind och
forsar. Så småningom lärde vi oss också att använda temperaturändringar
för att få gaser att ändra volym och därmed uträtta arbete.
Vi fann att alla förutsebara förändringar kunde omvandlas till nyttigt
arbete. Ju mer vi lärde oss om att omvandla olika förändringar till
arbete ju större blev behovet av ett begrepp och av måttenheter för
allt som kunde omvandlas till arbete. Vi började kalla allt som kunde
omvandlas till arbete för "energi".
Om vi har ett tillstånd som på något sätt avviker från det mest sannolika
kan vi förutse att detta kommer att förändras så att det närmar sig det
mest sannolika. En sådan avvikelse är alltså en potentiell förändring
d v s energi.
Att en förändring är förutsägbar innebär att vi kan beräkna dess storlek.
Men för sådana beräkningar behöver vi kvantitativa mått. Vi brukar då se
energi som en produkt av två mätbara storheter. Ofta gör vi den
uppdelningen så att den ena storheten kan betraktas som en mängdstorhet
(extensiv faktor) och den andra som en intensitetsfaktor (intensiv
faktor).
Energi är alltså ett kvantitativt mått på förutsägbar förändring.
Antag att en kula ligger på ett bord. Om kulan rullar över bordskanten
inträffar en förutsägbar förändring, kulan faller från bordet mot golvet.
Ju högre bordet är ju större är denna förutsägbara förändring och ju
tyngre kulan är ju större är förändringen. Vi säger att bordets höjd
gånger kulans tyngd är den förutsägbara förändringen som inträffar när
kulan faller från bordet, d v s bordets höjd gånger kulans tyngd är kulans
energi.
När vi talar om energianvändning menar vi att vi använder spontana förutsäg-
bara förändringar för att åstadkomma de förändringar vi önskar. Begreppet
"förutsägbarhet" är nära knutet till begreppet "användbarhet". Vill vi t ex
klyva ett vedträ försöker vi åstadkomma en situation där vi kan förutse att
vi får en förändring som resulterar i att vedträt klyvs. Vi sätter oss inte
och väntar på att slumpmässiga förändringar skall leda till att vedträt
spricker.
Med energikällor menar vi tillstånd som avviker från omgivningen på sådant sätt
att vi kan förutse att dessa avvikelser kommer att utjämnas.
Låt oss se på några exempel på avvikelser som vi anser användbara och avvikelser
som skulle kunna vara användbara.
Betrakta en avgränsad gasmängd, t ex en luftmassa. Låt oss först se på
molekylernas läge. Om medelvärdet av molekylernas avstånd till varandra
avviker från motsvarande medelvärde i omgivningen har vi en täthets-
avvikelse mellan gasmängden och omgivningen. Vi kan förutsäga att om
vi möjliggör utbyte med omgivningen kommer denna täthetsavvikelse att
utjämnas. Denna utjämning blir en förutsägbar förändring. Avvikelse i
medelavstånd betraktar vi som användbar energi.
Om molekylavståndets varians avviker från omgivningens kan vi förutsäga
att denna avvikelse kommer att utjämnas. Avvikelser i molekylavståndets
varians är alltså i princip användbara men vi känner ingen metod att
utnyttja dessa och betraktar dem därför inte som användbar energi.
Låt oss så se på tidsderivatan av läget, d v s på molekylhastigheten.
Om medelvärdet av molekylhastigheten avviker från motsvarande hastighet
i omgivningen har vi en vind som vi kan utnyttja. Vi kan t ex låta
hastighetsskillnaden utjämnas via en propeller på en vindsnurra. Utjämning
av skillnad i molekylernas medelhastighet betraktar vi alltså som
användbar energi.
Om molekylhastighetens varians avviker från motsvarande storhet i
omgivningen säger vi att vi har en temperaturavvikelse mot omgivningen.
Temperatur är ju molekylvikt gånger molekylhastighetens varians. På
1800-talet lärde vi oss att använda förutsägbara förändringar av
molekylhastighetens varians, d v s vi lärde oss att omvandla värme i
andra energiformer.
Avvikelser i medelvärde och varians för andra tidsderivatan av läget
borde också vara användbara. D v s avvikelser i medelvärde och varians
för molekylaccelerationen borde vara användbara. Men för andra tids-
derivatan har vi, lika lite som för högre derivator, någon praktisk
metod för energiomvandling.
Det är också så att ett tillstånd kan avvika från omgivningen på andra
sätt än de som karaktäriseras av medelvärde och varians. Det är inte
svårt att tänka sig osannolika fördelningar med samma medelvärde och
varians som omgivningen. Om en fördelning är osannolik kan vi förutsäga
att den spontant kommer att övergå till en mera sannolik. En sådan
fördelning är alltså användbar eftersom den ger en förutsägbar
förändring. Men frånsett ett fåtal osannolika tillstånd med avvikande
medelvärde och varians känner vi inte till praktiska metoder att
använda de osannolika tillstånd som omger oss. Och vi gör knappast
några försök att finna sådana metoder.
När vi pratar om energi brukar vi utgå från att vi skall använda
osannolikt stora avvikelser från medelvärde eller varians. Men för
ett tillstånd där avvikelserna är osannolikt små kan vi också förutsäga
hur tillståndet kommer att förändras. Här finns alltså en hel klass
"användbara" (i betydelsen förutsägbart föränderliga) tillstånd som
är lika stor som den dit alla våra kända energikällor hör men där vi
idag inte har någon aning om de kan användas praktiskt och i så fall
hur och till vad.
Att man kunde använda avvikelser i luftmolekylernas medelhastighet, d v s
vind, var känt sedan urminnes tid. Att segla med hjälp av vind är en
gammal konst. Att man även kan använda avvikelser i varians för luft-
molekylernas hastighet, d v s temperaturskillnader, för att driva maskiner
är en kunskap som bara är några få århundraden gammal. Det är naturligtvis
fullt tänkbart att vi om något århundrade betraktar användning av
avvikelser hos högre tidsderivator eller i fördelningsmått av högre
ordning som lika självklart som vi idag ser användning av värmemaskiner.
Att värme från brinnande olja skulle kunna driva en bil måste för 1700-
talets människor ha tett sig som helt otänkbart. Men trots det fanns det
de som försökte och gjorde detta möjligt att uppnå så småningom.
Vad är tid ?
============
Energi är förutsebara förändringar som vi genom förutsebarheten kan
utnyttja och omvandla enligt våra önskemål. Men vi behöver också ett
begrepp för och ett mått på alla förändringar som påverkar vår omgivning.
Summan av alla förändringar kallar vi tid.
Energi och tid är alltså mycket nära besläktade begrepp.Båda är
kvantitativa förändringsmått.
När vi använder energi använder vi en del av den förutsägbara delen av
de förändringar som utgör tidsflödet.
Varje märkbar förändring är en händelse och varje händelse är ett
tidsinkrement. I princip skulle vi kunna mäta tid i antal tidsinkrement
men det skulle bli ohanterligt stora tal för praktiskt bruk och vi brukar
därför använda enheten sekund som är ett visst (stort) antal tidsinkrement
eller år som är ännu fler tidsinkrement.
Händelser inträffar slumpvis men händelser kan vara kopplade så att
händelse A kan öka sannolikheten för händelse B.Om man kör en bil innebär
händelsen att framänden rör sig i förhållande till vägen att sannolikheten
för händelsen att bakänden skall röra sig i förhållande till vägen ökar.
Och det finns en kedja av kopplade händelser som via gasspjället,
förbränning i motorn och vridning av drivhjulen höjer sannolikheten att
bilen skall röra sig på vägen.
Ett sätt att beskriva tidsflödet kan vara att likna det vid lotterier.
Antag att man har 106 lotterier med vardera 106 lotter.
Varje lott motsvarar en potentiell händelse och varje vinst motsvarar att
händelsen inträffar. Om varje lotteri har 100 vinster är sannolikheten
att vinna i en dragning om man vet att man har en lott i rätt lotteri
1/104. Om man inte vet vilket lotteri man har en lott i blir sannolikheten
för vinst 1/1010. Koppling av händelser motsvaras av koppling av lotter
genom att de tillhör samma lotteri.
Om jag köper 103 lotter blir sannolikheten för vinst i varje dragning
1/107. När jag har fått 10 vinster kan jag alltså dra slutsatsen att det
har förekommit 108 dragningar vilket innebär att 1010 vinster
har fallit ut. Genom att följa vinstutfallet på min lilla lottbunt kan jag alltså
dra slutsatser om totala vinstutfallet i alla lotterier.
På motsvarande sätt kan vi avgränsa en grupp potentiella händelser och
genom att se hur många av dem som inträffar kan vi dra slutsatser om hur
många händelser som inträffar i hela universum. Vi kan t ex avgränsa en
svängande pendel, en oro, en kvartskristall eller en grupp cesiumatomer.
Kring detta avgränsade system kan vi bygga en klocka som mäter totala
antalet händelser i universum.
Det antal händelser som klockan mäter är en viss fast andel av totala
antalet händelser. För att få totala antalet händelser skall vi alltså
multiplicera det antal som klockan mätt upp med en konstant. Storleken
på denna konstant vet vi inte. Vi vet bara att det är en konstant.
Vi kan alltså inte fastställa konstantens värde men vi kan övertyga oss
om att det verkligen är fråga om en konstant.
Om våra klockor verkligen mäter totala antalet händelser i universum
skall alla klockor ange samma värde. Det är svårt att veta hur vi har
avgränsat våra klockor d v s att veta hur många lotter vi har köpt men
om de kan gå utan koppling till ovidkommande händelser skall det vara
möjligt att sätta på dem urverk med sådan utväxling att de går lika
fort. Och har vi en gång fått dem att gå lika fort skall de fortsätta
att göra det.
Vi finner då, mycket riktigt, att ju bättre vi kan avgränsa våra klockor
från koppling till ovidkommande händelser ju bättre går de. En svängande
pendel påverkas av vibrationer i upphängningen, temperaturvariationer,
luftrörelser mm. Men trots det visar olika pendelur påtaglig
överensstämmelse.
För en grupp cesiumatomer är möjligheten att undvika inverkan av
ovidkommande händelser betydligt bättre än för en pendel. Det är också
möjligt att bygga atomur som visar mycket god överensstämmelse.
Vad vill vi egentligen?
=======================
Teknik är att,via någon form av utväxling,anpassa extensiv och intensiv
faktor till vad vi har tillgång till.Till exempel att via ett spett
åstadkomma ökad kraft för att rubba en sten.
Teknik är också att utnyttja förutsägbara förändringar i vår omgivning till
att motsvara våra önskemål.Till exempel att använda den förutsägbara
förändringen när ett vedträ brinner genom att ta in det och tända det i
spisen när det är kallt i rummet.
Och teknik är också att analysera våra önskemål så att vi slipper anstränga
oss för sådant som vi inte är intresserade av.
Om Gustav III hade bestämt sig för att satsa på att kunna meddela sig
snabbare med Göteborg hade man hamnat i att bygga bättre vägar, att bygga
gästgivargårdar utefter vägarna och att avla fram bättre hästar. Vi hade
fått kurirer som på löddriga springare sprängde fram genom landet med brev
i postväskan.
När järnvägen kom fick vi, på köpet, snabbare brevbefordran.
Men den stora förändringen kom när man insåg att det handlade om att
överföra brevets innehåll, inte själva brevet. I vissa länder byggde man
optiska telegrafer där man från torn till torn överförde signaler genom
att en operatör i ett torn kunde se hur operatören i föregående torn
ställde sina signalskivor och så upprepa dessa inställningar i sitt torn
så att de kunde ses från nästa torn.
Vi ser den optiska telegrafen som ett monster av personalkrävande
ineffektivitet men när alternativet var kurirer ute på vägarna innebar
den en enorm besparing både av arbetskraft och överföringstid.
Med en elektrisk ledning mellan tornen kunde man signalera med större
tornavstånd. Och genom att man insåg att varje meddelande kan brytas ner
i binära bitar kunde man med morse-kod signalera via en enda tråd (eller
ett trådpar).
Genom att analysera vad vi egentligen önskade har vi alltså insett att
brevet inte var nödvändigt och att budskapet kunde reduceras till binära
bitar. Det har fört oss långt bort från hästavel och medfört att vi idag
tar för givet att överföringstid mellan Stockholm och Göteborg räknas i
millisekunder, inte i dagar.
När jag var liten, i mitten av 1900-talet, var det fortfarande vanligt
att man på vintrarna sågade upp is på sjöarna. Isblocken körde man hem
och lade i sågspånshögar så att man hade tillgång till is under sommaren.
I städerna använde man isskåp där maten hölls sval av is som man köpte av
en iskarl som åkte runt och sålde is. Många iskarlar trodde nog att de
faktiskt sålde is men en närmare analys av problemet ledde till insikten
att de sålde kyla och därmed till frågan om vilka möjligheter det fanns
att åstadkomma kyla. Och resultatet av den insikten blev Electroluxkylskåpet
och kompressorkylskåpet.
När man började bygga drivande och drivna maskiner behövde man göra en
uppdelning så att de som arbetade med att utveckla drivande maskiner kunde
arbeta utan att nödvändigtvis veta vad maskinen skulle driva och att de som
utvecklade drivna maskiner kunde arbeta utan att vara låsta till en viss
drivmaskin. Detta löste man med den roterande axeln som standardiserat
kopplingselement. En drivande maskin skulle alltid avslutas med en roterande
axel och en driven maskin skulle alltid försörjas via en roterande axel.
Sedan dess har elektrisk kraftöverföring utvecklats från att vara ett
alternativ för överföringar på några kilometer till att bli konkurenskraftig
på allt kortare överföringar. Möjligheten att styra strömmar med
halvledarteknik har idag medfört att elektrisk kraftöverföring mycket
ofta är konkurenskraftig även på de korta avstånd som den roterande axeln
använts för. Ett exempel som just nu är aktuellt är att ersätta
kardanaxelöverföringen i bilar med elektrisk kraftöverföring.
Insikten att den roterande axeln kan ersättas med andra kopplingselement,
t ex elektrisk, pneumatisk eller hydraulisk överföring, kommer att öppna
många av de låsningar som den roterande axeln medfört, t ex begränsningar
i rörelsemönster hos en kolv med vevstake och sinusformens dominerande
ställning inom elteknik.
Som exempel på undermålig teknik i dagens samhälle kan man nämna att vi
flyttar drygt ett ton bil för att flytta 80 kg människa och än värre att
vi inom kollektivtrafiken ofta flyttar tomma bussar på tiotals ton utan
att uträtta något önskat transportarbete över huvud taget.
Ett annat exempel är framdrivning av båtar. Vi utgår då från en fram- och
återgående kolv. Denna kolvrörelse omvandlar vi via ett vevparti till
rotation. Rotationen överför vi till en propeller som åstadkommer vatten-
rotation och framdrivning. För tändning och för försörjning av hjälpsystem
har vi också vanligtvis någon typ av elgenerator. En gång i tiden motiverades
övergången till rotation av att man använde svänghjul för att driva motorns
ickedrivande takter. Men med dagens magnetmaterial och halvledarteknik kan
man åstadkomma detta med elektrisk drivning vilket skulle innebära att man
slipper hela vevpartiet, alla problem med propelleraxelgenomföringar och alla
förluster i form av vattenrotation. Man kan i stället låta den fram- och
återgående kolven verka direkt mot vattnet.
De första och viktigaste frågorna som man alltid måste ställa sig vid
teknisk utveckling är alltså "Vad är önskat resultat?" och "Finns det
något enklare sätt att uppnå detta?".
Det finns en vandringssägen om hur man inom NASA drev ett projekt med
syfte att ta fram en lättare rakapparat som astronauterna skulle kunna
ha vid längre resor. Projektet pågick tills en av teknikerna gick ner
till butiken på hörnet och köpte en rakhyvel.
Hastighet
=========
Jag träffade en gång i tiden en pedagog som sa:
"När eleverna kommer till skolan vet de mycket väl vad hastighet är. Så
inför vi begreppet hastighet som kvoten mellan väg och tid och efter det
begriper de ingenting."
För att krångla till det ytterligare skulle jag vilja påstå att hastighet
är ett mått på hur stor andel av totala antalet händelser i universum som
flyttar en av de punkter som jag för tillfället är intresserad av i en viss
riktning.
Och så gäller det att reda ut det på ett begripligt sätt.
Betrakta en bil som kör på en väg. Lägg in ett koordinatsystem på sådant
sätt att lägeskoordinaterna för punkter i vägen förblir i stort sett
konstanta. När bilen fått upp farten kommer lägeskoordinaterna för en
partikel i bilen att ändras. Och denna partikel är kopplad till övriga
partiklar i bilen på sådant sätt att sannolikheten är stor att även
dessas koordinater skall ändras på liknande sätt.
Och varje gång en händelse inträffar i universum ökar tiden ett tids-
inkrement.
Om vi läser av lägeskoordinaterna för en partikel i bilen,väntar tills
tiden ökat med ett visst antal händelser (t ex en sekund) och därefter
på nytt läser av lägeskoordinaterna för partikeln får vi alltså veta hur
mycket partikelns läge ändrats under det att ett visst antal händelser
inträffat i universum. Men minsta detekterbara lägesförändring är en
händelse och att vi får veta hur mycket läget ändrats betyder alltså
att vi får veta hur många detekterbara lägesförändringar i rörelse-
riktningen partikeln gjort d v s hur många av alla händelser som inträffat
i universum som avsåg förflyttning av vår partikel i rörelseriktningen.
Om vi dividerar detta antal händelser med totala antalet händelser d v s
om vi dividerar lägesändringen för vår partikel med den tid som läges-
förändringen tagit får vi det som vi brukar kalla hastighet.
Vad jag gör när jag trampar ner gaspedalen i bilen är alltså att jag
försöker få en större andel av alla de händelser som inträffar i
universum att handla om att bilens läge på vägen ändras.
Om bilen flyttar sig sträckan s på tiden τ blir hastigheten v där
v = s/τ
Men om jag trampar på gasen ökar hastigheten. Om jag beräknar hastigheten
som s/τ får jag medelvärdet av hastigheten under tiden τ. Ibland är det vad
jag vill ha men ibland är jag mer intresserad av att veta hur stor
hastighet jag uppnått vid slutet av tiden τ (eller av något annat).
Hur beräknar man hastighet när den inte är konstant under mättiden?
Låt oss börja med att se på det enkla fallet att hastigheten är
proportionell mot tiden.Vi kan då skriva
v = a τ
där proportionalitetskonstanten a kallas för accelerationen.
Hur långt kommer ett föremål som från hastigheten noll accelererar med
accelerationen a under tiden τ?
Efter tiden τ är hastigheten v = a τ men medelhastigheten under tiden τ
blir hälften så stor d v s
v = a τ/2
medel
och sträckan s som föremålet tillryggalägger blir
s = v τ = a τ2 /2
medel
Men varför är det intressant att se på fallet med konstant acceleration?
Är det bara för att det är lätt att räkna på eller är det för att sådant
förekommer i verkligheten?
Om man påverkar ett föremål med konstant kraft får man faktiskt (bortsett
från luftmotstånd,friktion o dyl) konstant acceleration. Kraften F på ett
föremål med massan m ger accelerationen a enligt
F = m a
Och ett vanligt fall där man har konstant kraft är vid fallrörelser. Jordens
dragningskraft påverkar ett föremål vid jordytan med en kraft som är
praktiskt taget proportionell mot föremålets massa. När vi släpper ett
föremål och låter det falla fritt blir alltså accelerationen alltid densamma.
Vi får för fritt fall
a = 9,81 m/s2
För denna acceleration används ofta symbolen g.
Parametertid och koordinattid
=============================
Vi tänker oss en observatör som bara kan tänka i två dimensioner. Han ser
alltså världen projicerad på en yta på samma sätt som vi ser den med ett
öga eller när vi avbildar den med en kamera.
Om någon partikel ändrar höjd över denna yta förändras världen men det är
inte säkert att det märks i hans projektion. Indirekt kan han upptäcka
förändringen t ex genom att han flyttar sig så att partikelprojektionen
ändras. Han kan alltså ana sig till att hans bild är ofullständig och att
han bör ange denna typ av förändring genom att lägga till en tredje
koordinataxel.
På liknande sätt kan vi ana oss till att vi bör lägga till en tidsaxel
till vårt treaxliga rumssystem.
Om vi befinner oss i ett slutet rum,som vi kan kalla vårt observationsrum,
kan vi göra tankeexperimentet att vi bestämmer koordinaterna för alla
partiklar i rummet. Om vi så gör om bestämningen och finner att samtliga
koordinater är oförändrade är då allt oförändrat?
Nej det kan vi inte påstå för det kan ju ha inträffat händelser som förändrat
rummet i sin helhet i förhållande till världen i övrigt. För att ange det
behöver vi någon koordinataxel där vi kan avsätta observationsrummets läge
i förhållande till världen i övrigt. Vi kan kalla denna koordinat för
koordinattid.
Vi får då två tidsbegrepp som vi kan kalla
Parametertid
Koordinattid
Parametertid anger antalet händelser i universum oavsett var de inträffat.
Så snart någon partikel i universum ändrar läge så mycket att det är
detekterbart går alltså parametertiden ett tidsinkrement.
Koordinattiden går ett tidsinkrement varje gång en detekterbar händelse
inträffar utanför observationsrummet. En händelse som inträffar i
observationsrummet innebär att någon eller några rumskoordinater ändras
i observationsrummet. En händelse som inträffar utanför observationsrummet
innebär att koordinattiden ökar.
Antag att vi betraktar uppskjutning av en bemannad raket. Vi kan då lägga
x-axeln i raketens färdriktnig och strunta i y- och z-axlarna. Vi kan då
beskriva vad som händer i ett tvåaxligt koordinatsystem med en rumsaxel
(x-axeln) och en tidsaxel (koordinattid).
För oss är raketen en del av observationsrummet som ändrar läge i förhållande
till resten av observationsrummet. För besättningen ombord på raketen däremot
är raketens kontrollrum observationsrummet där,i stort sett allt står stilla.
Vi har lagt vår x-axel och vår axel för koordinattid så att huvuddelen av
vår omgivning har konstant x-koordinat medan raketens x-koordinat ökar.
Besättningen på raketen däremot lägger sin x-axel och sin axel för
koordinattid så att det mesta i raketen har konstant x-koordinat.
När raketen startar accelererar den men låt oss göra tankeexperinmentet att
den slår av motorn efter en stund och går med konstant hastighet. Dess bana
i vårt tvåaxliga koordinatsystem blir då en rät linje. Och besättningen på
raketen lägger sin axel för koordinattid längs denna räta linje. Raketens
hastighet innebär alltså att besättningens koordinatsystem vrids vinkeln
α i förhållande till vårt koordinatsystem. Och om vi mäter längd och
tid i samma enhet (t ex både längd och tid i meter eller både längd och tid
i sekunder) blir raketens hastighet sin α om vi använder parametertid
eller tan α om vi använder koordinattid.
 Fig 2
Eftersom raketen går sträckan x på vår parametertid τ eller på vår
koordinattid t säger vi att raketens hastighet är
x/τ = sin α
eller
x/t = tan α
Om hastigheten ökar så att raketen når ljushastigheten blir α 90 grader
och vår x-axel blir besättningens tidsaxel.
Att vi vanligen inte skiljer mellan parametertid och koordinattid beror på
att vi vanligen hanterar hastigheter som är så små i förhållande till
ljushastigheten att skillnaden mellan parametertid och koordinattid blir
liten.
Rörelseenergi
=============
Parametertid (τ) är alltså totala antalet händelser i universum,
koordinattid (t) är antalet händelser utanför observationsrummet och energi
(E)är den andel av totala antalet förutsägbara händelser som inträffar inom
observationsrummet.Om alla händelser inom observationsrummet kan anses vara
förutsägbara är
E = (τ - t)/τ
Vad blir då rörelseenergin för ett föremål, t ex en raket, som rör sig med
hastigheten v?
Enligt ovan gäller att
v = sin α
och om α är liten kan vi sätta
v = α
Av fig 2 framgår att
t = τ cos α = τ cos v
För små värden på v gäller att
cos v = 1 - v2 /2
vilket ger
(τ - t)/τ = v2 /2
Detta gäller för varje partikel i föremålet på en massenhet.Föremålets massa
m är antalet sådana partiklar och för hela föremålet får vi då rörelseenergin
E = m v2 /2
Intuition och konst
===================
När man kring mitten av det gångna årtusendet började verbalisera kunskap om
hur världen fungerade fick man nya möjligheter att utnyttja orsakskedjor och
förutsäga resultat av åtgärder. Sådan verbaliserad kunskap samlades och
systematiserades till det som brukar kallas vetenskap.
Men vetenskap omfattar inte allt.
Man säger att om fan skulle vilja luftkonditionera helvetet skulle han vända
sig till japanerna. De skulle göra en perfekt luftkonditionering utan att
ändra karaktären av helvete.
Läkarna talar om "Vetenskap och beprövad erfarenhet". Tekniska högskolor
lär ut "Konst och vetenskap". Man talar om "Ingenjörskonst".
Uppenbarligen inser man att det finns något som går utöver det som dagens
vetenskap omfattar.
I min ungdom byggde jag en gång en radio.Killen som stod vid arbetsbänken
intill frågade: "Vad ska det bli?". Jag svarade: "En radio". "Jaha! Men
varför är den så djävla ful?". Då slog det mig plötsligt att en radio var
något utöver beräkning av spolar, kondensatorer och motstånd. Det handlade
om att åstadkomma en produkt som skulle svara mot mänskliga önskemål. Och
en stor del av dessa önskemål låg utanför vetenskap och kunde enbart nås
via intuition. En intuition som krävde en speciell begåvning.
Under Kalle Ankas storhetstid tecknades Kalle av en tecknare som hette
Carl Barks. Att det blev en succe beror på att han hade denna begåvning att
"få till det". Med några få penndrag kunde han förmedla ett helt känsloliv
via ankbilder som inte ens hade mänskliga drag. Det finns t ex en bild i
Kalle Anka på Grönland där Kalle lurat iväg Alexander till Grönland och
inser att han har gått för långt. Han ser för sig en isbjörn som belåtet
klappar en fet mage med Alexanders damasker liggande framför sig på isen.
Och bilden av Kalle förmedlar hela den känslostorm som rasar inom honom.
Dagens tecknare har order att,så långt möjligt,efterlikna bilderna från
denna storhetstid.Vid första påseende är det hart när omöjligt att skilja
dem från en gammal klassiker. Men de förmedlar inga känslor!! De är
ritade för att efterlikna gamla, säljande bilder. Inte för att förmedla
upplevelser.
Och det samma gäller vår teknik att åstadkomma produkter. Det gäller inte
bara att få dem att fungera med hjälp av vetenskap.Det gäller att komma
längre än till att göra dem på rätt sätt. Det gäller att bli så säker på
hur man gör rätt att man vågar göra fel så att det blir bättre än rätt.
När vi har kommit dithän att alla kan få sina basala fysiologiska behov
uppfyllda måste vi gå vidare och ställa krav på,och tillåta, experiment
med nya ideer. Vi måste släppa fram något annat än massproduktion a la
dagens Kalle Anka. Något annat än efterapningar som är "tillräckligt bra".
Den verbaliserade vetenskapen kan beskriva en plog och namnge alla delar.
Den kan sätta upp kriterier för när man bör och när man inte bör plöja.
Den kan tala om vilken ände på plogen som skall vara framåt och vilka
delar som skall gå ner i jorden. Men den kan inte lära någon att plöja.
För att man skall "få till det", för att man skall få god skörd, för att
man skall vinna plöjningstävlan krävs något mer. Något som man bara kan
få genom kontakt med verkligheten.
De informationsmängder som skall bearbetas för att vi skall kunna räkna
oss fram till önskat resultat är ofta så enorma att vi måste utnyttja
genvägar som livet skapat under miljontals år av utveckling. Genvägar
som vi inte kan verbalisera, bara överföra via den gamla metoden från
mästare till lärling.
Kvantfysiken visade att vi inte kan härleda orsaker i all oändlighet,att
möjligheten att förutsäga vad som kommer att hända är begränsad.På liknande
sätt kan man säkerligen visa att möjligheterna att verbalisera all kunskap
är begränsad.Att vi behöver alla genvägar vi kan finna.Att vi borde vara
rädda om den overbaliserade kunskap som gångna generationer skapat.Att
dagens metoder att slå ut hantverk och konst med hjälp av det ekonomiska
systemet är mer än lovligt korkade.
Stabilitet
==========
Man upptäckte att det var möjligt att åstadkomma drivande maskiner som
omvandlade naturligt förekommande förändringar till användbar rörelse,
t ex till en roterande axel. Och man upptäckte att det var möjligt att
åstadkomma drivna maskiner som omvandlade en enkel rörelse, t ex en
vridning hos en roterande axel, till att utföra komplicerade sysslor.
Nu gällde det att "få till det"!
Ett problem som överraskade 1800-talets tekniker var att man fick
instabila system.
För att en maskin skall kunna utföra sin uppgift på rätt sätt krävs ofta
att någon eller något övervakar resultatet och styr maskinen efter vad
den åstadkommer. Detta kallas återföring.
Till en början använde man oftast människor som led i återföringslänkar.
För att styra en bil låter man en förare observera vägen och, via ratt,
gaspedal och broms, återföra styrsignaler till bilen. På ett fartyg lät
man styrmannen på bryggan observera och via maskintelegraf och maskinist
återföra styrsignaler till maskinen.
Men det visade sig snart att den långa återföringskedjan på ett fartyg
innbar problem. På den tid det tog för signalen att gå från styrman via
telegraf, maskinist och maskinpådrag kunde mycket oförutsett hända. Och
när bilarnas hastighet ökade blev förarens reaktionstid ett allt större
problem. I värsta fall kunde åtgärder som vidtogs för att avhjälpa ett
fel bli sådana som förvärrade det innan de nådde fram till verkställighet.
Stora tunga system blir ofta långsamma. Vi tycks ha en egendomlig vanföre-
ställning att en sådan långsamhet skulle göra det lättare att uppnå
stabilitet. Man försöker skapa stabila enheter genom att slå samman företag
till gigantiska koncerner och man lägger samman länder till handelsblock för
att få stora stabila enheter. Men man glömmer att den långsamhet som man
uppfattar som stabilitet beror på att systemen blir allt svårare att styra.
Att det tar längre tid för en supertanker än för en eka med aktersnurra att
ändra kurs betyder inte att det är lättare att styra en supertanker.
Och egentligen är det inte stabila system vi eftersträvar. Vi vill ha
system som skenar mot en bättre värld. Det är bara när det går åt fel håll
som vi har nytta av att veta hur vi uppnår stabilitet.
Första gången man kör en bil på isbana brukar man parera en sladd på sådant
sätt att den förvärras. Det är först efter en hel del träning som man lär
sig att häva en sladd. Vid första försöket blir styrningen ett instabilt
system som med växande rattutslag går mot att bilen stannar mot skyddsvallar
eller dylikt.
På vissa bandspelare används ett huvud för inspelning och ett för avspelning.
Om avspelningshuvudet sitter efter inspelningshuvudet kan man ansluta en
mikrofon och spela in sig själv samtidigt som man, med viss fördröjning,
lyssnar på resultatet. Men det brukar medföra att man förlorar talförmågan.
Korta och enkla ord brukar gå ganska bra men för mer komplicerade ord
lyssnar vi tydligen på oss själva så att vi kan rätta vårt uttal efter vad
vi hör. Men om vi inte hör vad vi säger när vi säger det utan vad vi sade
för en liten stund sedan fungerar inte detta. Metoden kan användas för att
testa om någon som påstår sig vara döv talar sanning men den är inte helt
tillförlitlig för även här kan vi, genom träning, lära oss att åstadkomma
ett godtagbart resultat även under dessa förhållanden.
När vi själva ingår i en överföringsloop från önskemål till verklighets-
förändring kan vi alltså ibland ändra vårt sätt att reagera så att vi
undviker oönskade resultat. Men om vi vill att ett tekniskt system
skall fungera på avsett sätt måste vi från början se till att vi inte
bygger in några instabiliteter i systemet. Servostyrningen i en bil skall
hjälpa till att vrida hjulen så mycket som vi vrider ratten, varken mer
eller mindre. Servobromsar skall ge en bromskraft som motsvarar
nedtryckningen av bromspedalen, varken mer eller mindre. O s v.
För att kunna studera stabilitetsproblem närmare måste man börja med att
välja någon typ av system som lätt kunde bli instabilt och som kunde anses
representativt för många olika fall av instabilitet. Ett sådant modellsystem
fann man i den återkopplade förstärkaren.
Fig 2
Eftersom raketen går sträckan x på vår parametertid τ eller på vår
koordinattid t säger vi att raketens hastighet är
x/τ = sin α
eller
x/t = tan α
Om hastigheten ökar så att raketen når ljushastigheten blir α 90 grader
och vår x-axel blir besättningens tidsaxel.
Att vi vanligen inte skiljer mellan parametertid och koordinattid beror på
att vi vanligen hanterar hastigheter som är så små i förhållande till
ljushastigheten att skillnaden mellan parametertid och koordinattid blir
liten.
Rörelseenergi
=============
Parametertid (τ) är alltså totala antalet händelser i universum,
koordinattid (t) är antalet händelser utanför observationsrummet och energi
(E)är den andel av totala antalet förutsägbara händelser som inträffar inom
observationsrummet.Om alla händelser inom observationsrummet kan anses vara
förutsägbara är
E = (τ - t)/τ
Vad blir då rörelseenergin för ett föremål, t ex en raket, som rör sig med
hastigheten v?
Enligt ovan gäller att
v = sin α
och om α är liten kan vi sätta
v = α
Av fig 2 framgår att
t = τ cos α = τ cos v
För små värden på v gäller att
cos v = 1 - v2 /2
vilket ger
(τ - t)/τ = v2 /2
Detta gäller för varje partikel i föremålet på en massenhet.Föremålets massa
m är antalet sådana partiklar och för hela föremålet får vi då rörelseenergin
E = m v2 /2
Intuition och konst
===================
När man kring mitten av det gångna årtusendet började verbalisera kunskap om
hur världen fungerade fick man nya möjligheter att utnyttja orsakskedjor och
förutsäga resultat av åtgärder. Sådan verbaliserad kunskap samlades och
systematiserades till det som brukar kallas vetenskap.
Men vetenskap omfattar inte allt.
Man säger att om fan skulle vilja luftkonditionera helvetet skulle han vända
sig till japanerna. De skulle göra en perfekt luftkonditionering utan att
ändra karaktären av helvete.
Läkarna talar om "Vetenskap och beprövad erfarenhet". Tekniska högskolor
lär ut "Konst och vetenskap". Man talar om "Ingenjörskonst".
Uppenbarligen inser man att det finns något som går utöver det som dagens
vetenskap omfattar.
I min ungdom byggde jag en gång en radio.Killen som stod vid arbetsbänken
intill frågade: "Vad ska det bli?". Jag svarade: "En radio". "Jaha! Men
varför är den så djävla ful?". Då slog det mig plötsligt att en radio var
något utöver beräkning av spolar, kondensatorer och motstånd. Det handlade
om att åstadkomma en produkt som skulle svara mot mänskliga önskemål. Och
en stor del av dessa önskemål låg utanför vetenskap och kunde enbart nås
via intuition. En intuition som krävde en speciell begåvning.
Under Kalle Ankas storhetstid tecknades Kalle av en tecknare som hette
Carl Barks. Att det blev en succe beror på att han hade denna begåvning att
"få till det". Med några få penndrag kunde han förmedla ett helt känsloliv
via ankbilder som inte ens hade mänskliga drag. Det finns t ex en bild i
Kalle Anka på Grönland där Kalle lurat iväg Alexander till Grönland och
inser att han har gått för långt. Han ser för sig en isbjörn som belåtet
klappar en fet mage med Alexanders damasker liggande framför sig på isen.
Och bilden av Kalle förmedlar hela den känslostorm som rasar inom honom.
Dagens tecknare har order att,så långt möjligt,efterlikna bilderna från
denna storhetstid.Vid första påseende är det hart när omöjligt att skilja
dem från en gammal klassiker. Men de förmedlar inga känslor!! De är
ritade för att efterlikna gamla, säljande bilder. Inte för att förmedla
upplevelser.
Och det samma gäller vår teknik att åstadkomma produkter. Det gäller inte
bara att få dem att fungera med hjälp av vetenskap.Det gäller att komma
längre än till att göra dem på rätt sätt. Det gäller att bli så säker på
hur man gör rätt att man vågar göra fel så att det blir bättre än rätt.
När vi har kommit dithän att alla kan få sina basala fysiologiska behov
uppfyllda måste vi gå vidare och ställa krav på,och tillåta, experiment
med nya ideer. Vi måste släppa fram något annat än massproduktion a la
dagens Kalle Anka. Något annat än efterapningar som är "tillräckligt bra".
Den verbaliserade vetenskapen kan beskriva en plog och namnge alla delar.
Den kan sätta upp kriterier för när man bör och när man inte bör plöja.
Den kan tala om vilken ände på plogen som skall vara framåt och vilka
delar som skall gå ner i jorden. Men den kan inte lära någon att plöja.
För att man skall "få till det", för att man skall få god skörd, för att
man skall vinna plöjningstävlan krävs något mer. Något som man bara kan
få genom kontakt med verkligheten.
De informationsmängder som skall bearbetas för att vi skall kunna räkna
oss fram till önskat resultat är ofta så enorma att vi måste utnyttja
genvägar som livet skapat under miljontals år av utveckling. Genvägar
som vi inte kan verbalisera, bara överföra via den gamla metoden från
mästare till lärling.
Kvantfysiken visade att vi inte kan härleda orsaker i all oändlighet,att
möjligheten att förutsäga vad som kommer att hända är begränsad.På liknande
sätt kan man säkerligen visa att möjligheterna att verbalisera all kunskap
är begränsad.Att vi behöver alla genvägar vi kan finna.Att vi borde vara
rädda om den overbaliserade kunskap som gångna generationer skapat.Att
dagens metoder att slå ut hantverk och konst med hjälp av det ekonomiska
systemet är mer än lovligt korkade.
Stabilitet
==========
Man upptäckte att det var möjligt att åstadkomma drivande maskiner som
omvandlade naturligt förekommande förändringar till användbar rörelse,
t ex till en roterande axel. Och man upptäckte att det var möjligt att
åstadkomma drivna maskiner som omvandlade en enkel rörelse, t ex en
vridning hos en roterande axel, till att utföra komplicerade sysslor.
Nu gällde det att "få till det"!
Ett problem som överraskade 1800-talets tekniker var att man fick
instabila system.
För att en maskin skall kunna utföra sin uppgift på rätt sätt krävs ofta
att någon eller något övervakar resultatet och styr maskinen efter vad
den åstadkommer. Detta kallas återföring.
Till en början använde man oftast människor som led i återföringslänkar.
För att styra en bil låter man en förare observera vägen och, via ratt,
gaspedal och broms, återföra styrsignaler till bilen. På ett fartyg lät
man styrmannen på bryggan observera och via maskintelegraf och maskinist
återföra styrsignaler till maskinen.
Men det visade sig snart att den långa återföringskedjan på ett fartyg
innbar problem. På den tid det tog för signalen att gå från styrman via
telegraf, maskinist och maskinpådrag kunde mycket oförutsett hända. Och
när bilarnas hastighet ökade blev förarens reaktionstid ett allt större
problem. I värsta fall kunde åtgärder som vidtogs för att avhjälpa ett
fel bli sådana som förvärrade det innan de nådde fram till verkställighet.
Stora tunga system blir ofta långsamma. Vi tycks ha en egendomlig vanföre-
ställning att en sådan långsamhet skulle göra det lättare att uppnå
stabilitet. Man försöker skapa stabila enheter genom att slå samman företag
till gigantiska koncerner och man lägger samman länder till handelsblock för
att få stora stabila enheter. Men man glömmer att den långsamhet som man
uppfattar som stabilitet beror på att systemen blir allt svårare att styra.
Att det tar längre tid för en supertanker än för en eka med aktersnurra att
ändra kurs betyder inte att det är lättare att styra en supertanker.
Och egentligen är det inte stabila system vi eftersträvar. Vi vill ha
system som skenar mot en bättre värld. Det är bara när det går åt fel håll
som vi har nytta av att veta hur vi uppnår stabilitet.
Första gången man kör en bil på isbana brukar man parera en sladd på sådant
sätt att den förvärras. Det är först efter en hel del träning som man lär
sig att häva en sladd. Vid första försöket blir styrningen ett instabilt
system som med växande rattutslag går mot att bilen stannar mot skyddsvallar
eller dylikt.
På vissa bandspelare används ett huvud för inspelning och ett för avspelning.
Om avspelningshuvudet sitter efter inspelningshuvudet kan man ansluta en
mikrofon och spela in sig själv samtidigt som man, med viss fördröjning,
lyssnar på resultatet. Men det brukar medföra att man förlorar talförmågan.
Korta och enkla ord brukar gå ganska bra men för mer komplicerade ord
lyssnar vi tydligen på oss själva så att vi kan rätta vårt uttal efter vad
vi hör. Men om vi inte hör vad vi säger när vi säger det utan vad vi sade
för en liten stund sedan fungerar inte detta. Metoden kan användas för att
testa om någon som påstår sig vara döv talar sanning men den är inte helt
tillförlitlig för även här kan vi, genom träning, lära oss att åstadkomma
ett godtagbart resultat även under dessa förhållanden.
När vi själva ingår i en överföringsloop från önskemål till verklighets-
förändring kan vi alltså ibland ändra vårt sätt att reagera så att vi
undviker oönskade resultat. Men om vi vill att ett tekniskt system
skall fungera på avsett sätt måste vi från början se till att vi inte
bygger in några instabiliteter i systemet. Servostyrningen i en bil skall
hjälpa till att vrida hjulen så mycket som vi vrider ratten, varken mer
eller mindre. Servobromsar skall ge en bromskraft som motsvarar
nedtryckningen av bromspedalen, varken mer eller mindre. O s v.
För att kunna studera stabilitetsproblem närmare måste man börja med att
välja någon typ av system som lätt kunde bli instabilt och som kunde anses
representativt för många olika fall av instabilitet. Ett sådant modellsystem
fann man i den återkopplade förstärkaren.
 Fig 3
Man utgår från en förstärkare som förstärker insignalen e med råförstärkningen
F till utsignalen c. När man ökar förstärkningen växer c och därmed βc och
närmar sig r. Det medför att e minskar och går mot noll när F går mot
oändligheten. För höga värden på F gäller alltså att
r = β c
c = r/β
Om man t ex vill åstadkomma ett förstärkarsteg med förstärkningen 10 gånger gör
man en spänningsdelare som ger β = 0,1. Även om F varierar mellan t ex
10 000 och 1000 000 gånger kommer då c att vara praktiskt taget 10 r.
Men ovanstående resonemang förutsätter att signalen inte fördröjs innan den
jämförs med r. Om en sinusformad signal fördröjs med halva periodtiden byter
den tecken. Då blir inte felsignalen skillnaden mellan r och βc utan summan
av r och beloppet av βc. Ökande F medför då inte att e minskar. e kommer
i stället att öka Om β F > 1 kommer då c att gå mot oändligheten oavsett
vad r är. Förstärkaren ger alltså ifrån sig en signal som är så stor att
förstärkaren bottnar oberoende av vilken insignal den fått.
Anordningen blir alltså instabil om det finns en frekvens där signalen fördröjs
en halv period samtidigt som β F (den s k loopförstärkningen) är större än 1.
Vanligtvis blir födröjningen allt större del av periodtiden när frekvensen ökar,
d v s fasvridningen ökar med ökande frekvens.
Ökande frekvens brukar också medföra att förstärkningen minskar.
Om man konstruerar en förstärkare och en återföringsloop så att β F < 1 när
fasvridningen blir 180 grader får man alltså en stabil förstärkare.
Genom att ersätta tidsfunktionerna r , e , c , F och β med motsvarande
Laplacetransformer får vi en möjlighet att samtidigt hantera amplitud och
fördröjning. Metoden är teoretiskt elegant och i vissa sammanhang användbar
men den ställer ganska stora krav på att användaren behärskar övergången
mellan tidsfunktioner och Laplacetransformer.
Ett annat sätt att samtidigt hantera amplitud och fördröjning är att använda
komplexa tal. En signal kan delas upp i och beskrivas som en summa av
sinusformade signaler (Fourier-uppdelning). En beskrivning av hur en
förstärkare uppför sig för sinusformade signaler av olika frekvens ger
alltså en fullständig bild av hur förstärkaren uppför sig för godtyckliga
signaler. Man kan då använda komplexa tal där beloppet motsvarar
amplitud och argumentet motsvarar fasvridning. Man kan då i det
komplexa talplanet rita kurvor som visar hur förstärkningen blir vid
olika frekvenser. Om en sådan kurva omsluter punkten -1 + i0 är
förstärkaren instabil (Nyquist-kriteriet).
Ett annat sätt att formulera Nyquist-kriteriet är: Om förstärningen vid
någon frekvens ger fasvridningen 180 grader samtidigt som dess
belopp är större än 1 blir förstärkaren instabil.
Det går alltså att formulera villkor för stabilitet hos den återkopplade
förstärkaren och i många andra sammanhang kan man se att förhållandena
kan hanteras på samma sätt.
DEL 3
Hur fungerar världen?
=====================
Aristoteles (384 - 322 f Kr) gjorde en ganska omfattande sammanställning av
vad som då var känt.Han och hans efterföljare sa i princip:
Världen är vad den synes vara eller borde vara
Tunga föremål faller fortare än lätta.Stora hus är större än små och skall
alltså avbildas större.Solen och stjärnorna rör sig över himlen.Det finns
fyra aggregationstillstånd jord = fast fas , vatten = vätska , luft = gas ,
eld = plasma och kanske ett femte "de vises sten" = kollapsad stjärnmateria
och av dessa tillstånd är allt uppbyggt.
I stort sett stod sig denna uppfattning i ett och ett halvt årtusende.
Världen fungerade enligt av Gud givna lagar.Men Gud kunde bryta mot lagarna
och bistå enskilda människor.Och han var stor nog att bry sig om varje
människa.Det kunde löna sig att be om underverk,särskilt om man anlitade
prästerlig konsulthjälp.
Men tankebyggnaden började knaka i fogarna.Om man avbildade stora hus små
när de var långt borta blev bilderna mer lika verkligheten än när man
använde "korrekt" storlek.
Copernicus (1473 - 1543) visade att man fick en enklare bild av verkligheten
om man tänkte sig att jorden roterar kring sin axel och kring solen.
Galilei (1564 -1642) spädde på med att visa att man kunde se Jupiters månar
rotera kring planeten om man använde en kikare.Och han visade även att
påståendet att tunga föremål faller fortare än lätta bara gäller om de
lätta har större luftmotstånd i förhållande till sin vikt.
Påven, som såg hur fotfästet för hela världsuppfattningen höll på att gå
förlorat, försökte förgäves stoppa sådana ideer.
Newton (1642 -1727) visade att händelseförlopp kunde beräknas och förutses i
en utsträckning som man dittills inte kunnat tänka sig.Guds ingripanden
behövdes i långt mindre omfattning än vad man föreställt sig tidigare.En stor
del av förtröstan på Guds godhet kunde flyttas över på en förlitan på att
världen var förutsägbar.Gud hade skapat världen så att han mycket sällan
behövde ingripa. Världsuppfattningen fick ett nytt fotfäste.
För närobservationer använder vi känsel,hörsel,lukt,smak och syn men för fjärr-
observation är vi praktiskt taget helt hänvisade till synen.Kunskap om ljus
spelar därför en avgörande roll för vår världsuppfattning.Maxwell (1831 - 1879)
gav med den elektromagnetiska ljusteorin en mycket elegant beskrivning av ljus.
Men han väckte också en besvärlig fråga.
Maxwells ekvationer beskriver ljus som en vågrörelse mellan elektriskt och
magnetiskt fält.Men det finns ingen knytning av denna vågrörelse till ett
vågbärande medium. Vattenvågor bärs av vatten,ljudvågor bärs av luft och vi
kan definiera vågornas hastighet i förhållande till vattnet eller luften.
Och om vattnet eller luften strömmar påverkas även vågornas rörelse. Men
Maxwells ekvationer visade inte på något sådant för ljus!!
När Michelson (1852 - 1931) och Morley försökte mäta jordens hastighet
i förhållande till den ljusbärande världsetern blev resultatet noll.Liksom den
fasta jorden hade rubbats av Copernicus sviktade nu den fasta världsetern.
Einstein (1879 - 1955) hävdade att vi måste överge föreställningen att alla ser
samma värld.Om två observatörer rör sig i förhållande till varandra upplever de
att den andres klocka och meterstav påverkas av rörelsen.
Heisenberg (1901 - 1976) visade att vi inte samtidigt kan mäta tid och energi
med hur stor noggrannhet som helst.Och mätningarna påverkar vad vi mäter.Trots
att vi kommit på hur man kan bygga förstärkare som förstärker en signal till
vilken styrka som helst finns det gränser för hur noggrant man kan mäta.
Fotfästet i en av Gud given värld som är oberoende av alla observatörer sviktade.
Men om vi delar upp tidsbegreppet i koordinattid och parametertid där
koordinattid är en rumskoordinat likvärd de övriga tre och parametertiden är
en förändringsparameter då kanske vi åter kan se en eter,ett alluppfyllande
Brahma.Ett Brahma som strömmar med ljushastighet som en etervind. En etervind
som vi svävar i som ballonger eller moln som följer vinden. En vind som kan
blåsa åt olika håll i det tredimensionella rummet genom att etern är
kompressibel och/eller att etervinden i koordinattidsled kan variera. En värld
som är lika för alla betraktare men där den tredimensionella projektionen av
den fyrdimensionella världen kan variera för olika betraktare.
Vad är verklighet?
==================
Vi lever i en värld som förändras.Denna värld observerar vi med
sinnen som registrerar förändringar.
Om man sätter ett finger mot en bordsyta känner man när fingret
vidrör bordsytan.Men om man håller kvar fingret försvinner
känslan.Vårt känselsinne registrerar alltså inte kontakten med
bordsytan utan bara förändringen när fingret sätts mot bordet.
Om man håller ögonen orörliga under tillräckligt lång tid för-
svinner synintrycket.För att vi skall se något räcker det inte
med förändringarna när enskilda fotoner träffar näthinnan.Hela
mönstret i bilden måste förändras för att vi skall se något.
Vi ser inte världen sådan den är.Vi ser förändringar av världen.
Det vi upplever som verklighet är alltså inte verkligheten utan
förändringen av verkligheten.Vi ser inte verkligheten utan verk-
lighetens tidsderivata.
Bakom den verklighet vi upplever när våra sinnen registrerar
förändringar finns alltså en verklighet som förändras.
Ett föremål som ett hus kan förefalla vara en stabil oföränder-
lig företeelse men för att vi skall kunna veta att det finns
måste det förändra ljusstrålar som faller på det eller stoppa upp
vår handrörelse när vi tar på det.Våra sinnen registrerar alltså
enbart förändringar runt huset.Vi kan bara indirekt sluta oss
till att huset finns.
Våra sinnen informerar oss om förändringar i vår omvärld och vi
finner att många av dessa kan beskrivas genom att vi antar att
det finns en bakomliggande verklighet som orsakar dessa föränd-
ringar.Utifrån de förändringar vi registrerar kan vi dra vissa
slutsatser om denna verklighet men vi kan inte få veta allt om
den.
Om världen kan beskrivas av någon sorts funktion som har en tids-
derivata och om vi kan registrera tidsderivatan kan vi integrera
denna tidsderivata för att komma till ursprungsfunktionen.Men vi
vet att integration ger en obestämd integrationskonstant.Tids-
derivatan innehåller alltså inte all information om ursprungs-
funktionen.
Den värld vi upplever med våra sinnen är alltså förändringar av
en bakomliggande verklighet.Och för de flesta av oss gäller att
all vår strävan går ut på att styra dessa förändringar och
därigenom anpassa världen efter våra önskemål.
För att vi skall kunna uppfatta något måste världen innehålla
företeelser som avviker från omgivningen (kvanta) och dessa måste
bilda händelser genom att ändra läge i förhållande till varandra.
Vi kan inte se kvanta bara händelser.
För att observera något måste vi förändra det vi observerar. Det
är bara genom att se hur det förändras som vi kan dra slutsatser om
hur det ser ut. Vi kan inte komma fram till "das Ding an sich", till
verkligheten sådan den är. Vi kan bara föreställa oss en verklighet
som förändras på det sätt som vi observerar.
Ju noggrannare vi mäter ju mer förändrar vi det vi mäter. Om vi vill
veta allt om hur stenarna ligger i ett tegelhus måste vi plocka bort
alla stenar och förändra huset till en tegelstenshög. Men så brukar
vi inte göra. Vi nöjer oss med att se ytan på ytliga stenar och
kanske plocka bort ett par stycken. Så antar vi att övriga stenar
ligger på samma sätt, d v s att mönstret upprepas. Det mesta av vår
världsuppfattning bygger på denna föreställning om mönsterupprepning.
Vi föreställer oss en värld där mönster upprepas som tapetmönster. En
värld där förändringar kan inträffa och bilda händelser som vi kan
registrera med våra sinnen så att vi kan dra slutsatser om hur mönstren
ser ut.
Denna mönsterupprepning är ett av de största mysterierna. Vi vet inte
varför det är så och mycket lite om de regler som den följer.
Plancks konstant - Alltets konstant
===================================
Betrakta ett universum som innehåller h stycken urskiljbara kvanta. Varje
sådant kvanta är så litet att det inte går att dela. Det kan bara finnas
eller inte finnas. Vi kan kalla ett sådant kvanta för enhetskvanta eller
på engelska unit-quanta och beteckna det med UQ. Sorten för h blir alltså UQ
Den minsta händelse som kan inträffa i detta universum är minsta detekterbara
lägesförändring för ett enhetskvanta i förhållande till övriga kvanta. En
sådan händelse kan vi kalla för enhetshändelse eller på engelska unit-event
och beteckna med UE.
Alla händelser kan delas upp i enhetshändelser men en enhetshändelse kan inte
delas upp. Den 'inträffar' eller 'inträffar icke'. Något däremellan finns inte.
Totala antalet enhetshändelser som någonsin inträffat i vårt universum kallas
för absolut tid ( egentligen absolut parametertid). Tidpunkten för en viss
händelse är totala antalet enhetshändelser som inträffat före händelsen.
Tiden mellan händelse A och händelse B är tidpunkten för händelse B minus
tidpunkten för händelse A. Tid betecknas med τ och sorten för tid blir
alltså UE.
Antag att vi intresserar oss för en viss del av vårt universum, t ex av en
kula. Av alla kvanta i universumet avgränsar vi då några som utgör kulan. Vi
kan beteckna dessa kvanta med E. Med E menar vi alltså ett visst antal
enhetskvanta och sorten för E blir alltså UQ. Då gäller att E/h anger hur
stor del av universum som kulan utgör.
Om det så inträffar en enhetshändelse är sannolikheten E/h att denna
enhetshändelse består i att något av de kvanta som utgör kulan ändrar läge.
På tiden τ inträffar τ enhetshändelser och varje gång är sannolikheten
E/h att något av de kvanta som utgör kulan ändrar läge. I uttrycket
τ E
a = -----
h
är alltså a det antal gånger som ett enhetskvanta som ingår i E ändrar läge
under tiden τ. Om man minskar τ och/eller E så att a blir mindre än ett
övergår a till att ange sannolikheten att något kvanta inom E ändrar läge under
tiden τ.
τ E UE UQ
Sorten för a = ----- blir ----------- d v s UE.
h UQ
Om vi avgränsar en så liten mängd kvanta ΔE och observerar den under så kort
tid Δτ att Δτ ΔE = h/2 kommer endast en halv enhetshändelse att
beröra ΔE d v s sannolikheten att någon händelse inträffar som berör ΔE blir
0,5. Detta är gränsen för att vi skall kunna se att något händer med ΔE.
(Heisenbergs osäkerhetsrelation).
Låt oss se på ett litet universum med h = 1000 UQ där vi avgränsar en kula
med E = 10 UQ. Det är då bara var hundrade UQ som tillhör E. Det är alltså
bara var hundrade enhetshändelse som innebär att något kvanta i E har
flyttats. Efter en förändring av E går det alltså 100 UE innan det på nytt
är dags för en förändring av E. Vi säger att E:s periodtid är 100 UE.
Periodtid betecknas T och har sorten UE. För att bestämma periodtiden
sätter vi a = 1 i uttrycket τ = a h/E och får alltså T = h/E. Egentligen
är alltså T = 1 h/E där 1 har sorten UE så att även T får sorten UE.
Inverterade värdet av periodtiden kallas för frekvens.
Frekvens betecknas f och har sorten UE-1. Frekvensen för E är
f = E/h alltså egentligen f = E/(1 h) där ettan har sorten UE.
h är alltså antalet enhetskvanta i hela universum. Sorten för h är alltså UQ.
Men h är också det antal enhetshändelser som erfordras för att rubba samtliga
enhetskvanta i universum. Ser vi det så har h sorten UE. Och om en viss
enhetshändelse inträffar är h det antal enhetshändelser som troligen inträffar
innan den upprepas. Även om vi ser h på det viset blir sorten UE.
Även om alltså sorten för h inte är helt entydig är värdet entydigt för ett
visst universum. För alla i vårt universum har h samma värde. Men trots det
har vi ingen bra metod att fastställa detta värde. Vi vet inte exakt hur stort
vårt universum är och därmed vet vi inte heller det exakta värdet på h. Vi har
alltså inget bra värde på h varken i sorten UQ eller UE. Om vi vill kan vi
emellertid vända på resonemanget och säga att vi mycket väl vet värdet på h
men vi vet inte hur stort ett enhetskvanta är och därför kan vi inte uttrycka
h i sorten UQ.
Vi använder inte enheterna UQ ch UE för att ange kvantamängder och tider.
Detta beror dels på att det skulle bli svårhanterligt stora tal dels på att
vi inte exakt kan fastställa storleken på ett UQ och på en UE. Vi använder
i stället sorter som Joule och sekund som är ett stort antal UQ resp UE.
På en sekund går det ett visst antal (ks) enhetshändelser. På en
Joule går det ett visst antal (kJ) enhetskvanta. För att avgöra
vad som händer med värdet på h om vi övergår till att ange τ i sekunder
och E i Joule kan vi utgå från uttrycket τ E = a h. Om vi övergår till
sekunder och Joule får vi
τ ks E kJ = a h
a h
τ E = --- ---
ks kJ
Vi bibehåller sorten UE för a och får då
h i Js lika med (h i UQ)/(ks kJ)
Sorten för h är inte entydig eftersom ett enhetskvanta under vissa
omständigheter motsvaras av en enhetshändelse. h får då samma värde
oberoende av om vi använder sorten UQ eller UE. Men använder vi i
stället sekund och Joule måste omräkningsfaktorerna komma på rätt
plats och vi får då entydigt sorten Js för h.
h kallas för Plancks konstant.
Bortom tid och rum
==================
När vi som barn blir medvetna om vår omgivning börjar vi fråga "Vad
finns bortom?" , "Vad fanns före?" och "Vad kommer efter?".Och varje
gång vi får ett svar förskjuter vi gränserna för den värld vi upplever
som känd och ställer på nytt samma frågor.
Till slut brukar vi bli avspisade med att frågorna är meningslösa och
att ingen kan svara på dem.Men så är det faktiskt inte.Vi kan faktiskt
ibland hitta absoluta gränser.Det kanske mest iögonfallande exemplet är
absoluta nollpunkten för temperatur.
När man upptäckte att gaser ökade tryck och/eller volym när man värmde
dem fick man ett sätt att mäta temperatur.Vår instinkt att fråga "Vad
finns bortom?" ledde till att man började fundera kring frågan "Hur
kallt kan det bli?".Och svaret var faktiskt inte "Hur kallt som helst".
Om man kylde en gas vid konstant tryck minskade dess volym.Men till slut
kom man till volymen noll.Och eftersom vi inte kan tänka oss vad negativ
volym skulle kunna vara insåg man att det finns en absolut nollpunkt för
temperatur.
När vi tittar på en avlägsen stjärna tittar vi inte bara långt bort, vi
tittar även bakåt i tid.Vi ser inte stjärnan sådan den ser ut nu utan
sådan den såg ut när ljuset lämnade den. Om solen plötsligt slocknade
skulle vi inte märka något förrän det gått 8 minuter. Fram till dess
skulle ljus som var på väg mot oss när den slocknade fortsätta att komma
fram. Vi ser alltså inte solen sådan den är utan solen för 8 minuter
sedan.Och avlägsna stjärnor kan vi se för miljarder år sedan.
Liksom man en gång i tiden undrade hur kallt det kunde bli kan vi fråga oss
hur långt och hur långt tillbaka vi kan se. Och även här är faktiskt inte
svaret "Hur långt som helst".
Ljus kan uppfattas som en vågrörelse och färger som frekvensen hos denna
vågrörelse. Blått ljus har hög frekvens och rött ljus har lägre frekvens.
Vitt ljus är en blandning av olika färger d v s av olika frekvenser men
blandningen är inte jämn. Frekvenserna är koncentrerade till s k
spektrallinjer som motsvarar egenskaper hos de ämnen som avgivit ljuset.
Spiller man lite saltvatten i lågan på en gasspis lyser lågan med en gul
färg som motsvarar en kraftig spektrallinje hos det natrium som ingår i
saltet.
När vi tittar på ljus från fjärran stjärnor finner vi att färgen har
förskjutits mot rött. Och det är inte fråga om en omfördelning av
färgintensiteter för alla spektrallinjer har fått lägre frekvens. Det är
alltså så att ljusets frekvens blir lägre ju längre bort vi tittar.
Det innebär att om vi tittar tillräckligt långt bort blir ljusets frekvens
noll.
Och liksom vi inte kan tänka oss en negativ volym kan vi inte tänka oss en
negativ frekvens. Vi kan alltså inte ha större avstånd än att ljuset som når
oss från det avståndet får frekvensen noll. Och vi kan inte ha längre tid
tillbaka än gångtiden för ljus som når oss från detta avstånd.
Hur ser då världen ut när vi kommer till största möjliga avstånd? Vi "ser"
där en värld som avger ljus med frekvensen noll d v s totalt mörker. En
värld där vi inte kan urskilja någonting. Där vi inte kan skilja två punkter
från varandra och alltså inte tala om deras läge och avstånd. En värld där
vi inte kan urskilja punkter så att vi kan säga att en händelse har inträffat
genom att deras läge har förändrats. En värld utan avstånd och utan händelser
d v s en värld utan rum och tid.
Man brukar uppskatta det största möjliga avståndet till mellan 10 och 20
miljarder ljusår och motsvarande tid blir alltså mellan 10 och 20 miljarder
år.
Rum och tid är alltså ändliga begrepp som endast har mening lokalt i den
värld där vi råkar befinna oss. Utanför denna världs rum och tid råder en
jämn fördelning, d v s ett totalt mörker där allt överallt är lika. Vi
kommer ur ett totalt mörker, vi går mot ett totalt mörker och vi omges
av ett totalt mörker. Men den störning av detta perfekta tillstånd som
vi kallar världen är tillräckligt stor för att vi skall kunna ha en hel
del skoj på vägen.
Tid
===
En stillastående värld är ointressant.
Det finns en gammal film,jag tror den hette "A kind of stopwatch" om en man med
ett stoppur som har den egenskapen att när han startar det stannar allt i hela
världen utom han själv.Han använder det för att plundra en bank där han i lugn
och ro kan gå omkring bland stillastående kunder och tjänstemän.Men när han skall
trycka igång världen igen tappar han uret i golvet så att det går sönder och han
blir fast i en meningslös stillastående värld.
Lyckligtvis står vår värld inte stilla.Den är stadd i ständig förändring.
För att få ett mått på världens förändring kan vi dela in den och se den som
summan av en massa små händelser.
Den minsta händelse vi kan observera innebär att någon urskiljbar punkt
förändrar sitt läge i förhållande till övriga urskiljbara punkter med den
minsta detekterbara lägesförändringen.Vi kan kalla en sådan händelse för
en enhetshändelse.Så kan vi dela in världens förändring i enhetshändelser
(det blir ett stort och ohanterligt tal men det blir ett ändligt tal).
Enligt föregående avsnitt kan vi finna en gräns för hur långt tillbaka vi
kan gå och vi kan alltså finna en siffra som anger totala antalet
enhetshändelser sominträffat i vår värld.Siffran blir stor och vi har inte
mätmetoder som gör att vi kan bestämma den särskilt noggrant men vi kan
konstatera att denna siffra finns och vi kan kalla den för "absolut tid".
Vi kan uppskatta den absoluta tiden till att nu vara c:a 15 10120
enhetshändelser.
Det finns en mängd olika uppskattningar av Hubble-konstanten men låt oss
anta att universums ålder är 15 miljarder år och radien 15 miljarder ljusår.
Medeltätheten kan uppskattas till 4 10-26 kg/m3. Vilket innebär att
totala innehållet är 2 1053 kg eller 2 1070 J.Om vi dividerar med Plancks
konstant får vi motsvarande frekvens som alltså blir 3 10103 Hz.
Inverterar vi det värdet får vi periodtiden som vi kan använda som mått på
kortast möjliga tid d v s som mått på den tid som åtgår för en enhetshändelse.
Vi får alltså fram att det går 3 10103 enhetshändelser på en sekund och
att en enhetshändelse tar 3 10-104 s.Då 15 miljarder år är 5 1017 s
innebär det att den absoluta tiden nu är c:a 15 10120 enhetshändelser
Men även om vi inte kan bestämma den absoluta tiden särskilt noggrant och även om
den absoluta tiden blir ohanterligt stor kan vi,med stor noggrannhet,mäta tiden
mellan två händelser som inträffar inom vårt observationsområde.
Av alla händelser som inträffar i universum är de allra flesta helt slumpmässiga.
Det är bara en mycket liten del som vi kan påverka.Men enhetshändelser har en
tendens att bilda mönster och samordnas till större händelser som vi kan
observera.Eftersom sådana inträffar helt slumpmässigt kan vi utgå från att om
vi nöjer oss med att observera en viss typ av händelse inom ett litet område så
får vi ett mått på totala antalet händelser.Vi kan t ex bygga ett pendelur och
räkna med att varje gång händelsen att pendeln fullbordat ett slag har inträffat
har det gått en sekund d v s har det inträffat 3 10103 enhetshändelser i hela
universum.Att den andel av det totala antalet händelser som vi mäter på detta sätt
är konstant kan vi övertyga oss om genom att göra två likadana klockor och se
om de går likadant.Vi finner då att om vi kan isolera dem från störande
inverkan utifrån går de nästan exakt lika.
Rum
===
På liknande sätt som vi kan definiera en enhetshändelse kan vi definiera en
enhetslängd.En enhetslängd är helt enkelt den sträcka ljuset hinner gå under en
enhetshändelse.
Vårt universum blir då ett rum i form av ett klot med radien 15 10120 enhetslängder.
Detta klot kan vi dela in i enhetsceller med en enhetslängd som sidlängd.Detta
klot rymmer alltså c:a 1 10364 enhetsceller.
Om vi även vill räkna in alla enhetsceller som någonsin funnits får vi betrakta
tid som en fjärde dimension.Vi får då ett fyrdimensionellt halvklot med c:a
1 10485 enhetsceller.
En enhetscell ligger på gränsen till att vara observerbar.Det går alltså inte att
urskilja några detaljer i den.Vi kan bara skilja mellan om den innehåller något eller
om den är tom.Vi kan alltså fullständigt beskriva den med en etta eller en nolla.
Världen är alltså ett "datorminne" som rymmer 10364 bits och som totalt
har hanterat 10485 bits.
Med "avstånd" mellan A och B menar vi det antal enhetsceller vi måste passera för att
komma från A till B.
Vi kan alltså se på världen som en dator med ett enormt minne.Men en dator är
praktiskt taget oanvändbar om den inte har ett operativsystem som gör att innehållet
i minnet ändras enligt vissa regler.Och även världen har sitt "operativsystem".Hur
detta fungerar är vad fysik egentligen handlar om.
Orsak och verkan
================
För att bli användbar behöver en dator något operativsystem med någon form av BIOS
(Basic In/Out System).Ännu mer fundamentalt är att man redan i processorns hårdvara
brukar lägga in vissa begränsningar av hur minnet kan förändras.Man brukar t ex
dela in minnet i grupper om 8 , 16 eller 32 bits som hanteras samtidigt.
För att kunna använda datorn måste vi komma fram till en förenklad uppfattning av
den,en uppfattning som är användbar och som kan rymmas inom vår tankeförmåga.Vi
börjar då med att bortse från ettor och nollor för att i stället se grupper av
bits som vi kallar bytes.
På liknande sätt finner vi att världen har ett "BIOS" som grupperar enhetsceller.
Sammanhängande grupper av enhetsceller kallar vi partiklar och vi finner att det
finns förvånansvärt stabila sådana.Av någon anledning förblir mönstret av ettor
och nollor inom en partikel ofta konstant även om partikeln ändrar läge i
förhållande till andra partiklar.
Ett sätt att se detta bevarande av mönster är att jämföra med ballonger i
byig vind. Dessa flyttas av vindbyar så att de ändrar läge i förhållande till
varandra men om ballongerna ligger tätt kommer inte en vindby att ändra det
inbördes läget för närliggande ballonger.
Även i tidsled grupperar världens "BIOS" enhetshändelser till händelsekedjor som
bildar urskiljbara mönster.Om vi vet vad som har hänt kan vi,i vissa fall,förutse
vad som kommer att hända.Om vi vet att en partikel har förflyttat sig i ett område
med enbart nollor kan vi förutse att den kommer att fortsätta förflyttningen.
Vi kallar den förflyttning som redan skett för orsak och den som vi förutser för
verkan.
Vi har funnit ett antal orsak-verkan-samband som vi kan använda som ett sorts
högnivåspråk för programering av världen.Om vi önskar en viss verkan men finner
att den är svår att uppnå kan vi leta bland dessa samband för att se om vi i
stället kan finna en orsak som är lätt att åstadkomma och som ger önskad verkan.
Eller en orsak som har en verkan som kan vara orsak till den önskade verkan.Eller
en orsak till en orsak till en orsak till verkan.
Människor har naturligtvis alltid använt sig av orsakskedjor för att nå sina mål.
Men till en början skedde detta huvudsakligen intuitivt.Att orsaka en spräckning
av ett flintstycke så att man får en användbar flintkniv är en konst som våra
förfäder utvecklade och förfinade.Man lärde sig orsakskedjorna men man
verbaliserade dem inte.Lärlingen lärde sig huvudsakligen genom att se och höra
mästarens slag och genom att själv slå med slagsten på flinta.
Kring mitten av det gångna årtusendet började en målmetveten strävan att
verbalisera orsak-verkan-samband.Detta lyckades över förväntan och så sent som
under adertonhundratalets slut trodde man på fullt allvar att varje verkan
kunde knytas till orsaker som i sin tur kunde knytas till orsaker.
Kvantfysiken och speciellt Heisenbergs osäkerhetsrelation bröt med denna
föreställning genom att hävda att ett orsak-verkan-samband säger att en orsak
innebär en viss sannolikhet för en viss verkan.Denna sannolikhet kan vara nära
ett men den är alltid mindre än ett.
Om man släpper en sten är sannolikheten stor att den faller nedåt.Men det finns
en liten,beräkningsbar,sannolikhet att den faller uppåt.Denna sannolikhet är
naturligtvis så liten att vi,för praktiskt bruk,kan strunta i den.Men att den
finns är principiellt viktigt för det innebär att världen kan komma med
överraskningar.
Heisenbergs osäkerhetsrelation bygger på insikten att världen både har partikel-
karaktär och vågkaraktär samtidigt.Men en våg måste observeras under åtminstone
större delen av periodtiden innan man kan veta att det verkligen rör sig om en
våg.En ansamling fyllda enhetsceller,d v s en ansamling ettor,kan bilda en
partikel.Ju fler ettor den innehåller ju högre säger vi att dess energi är.
Och när vi använder vågbeskrivning blir dess frekvens energin dividerad med
Plancks konstant.Ju högre energi den har ju högre frekvens och därmed kortare
periodtid har den.
Något förenklat kan man säga att Heisenberg påpekade att man måste observera
en energimängd under halva dess periodtid innan man säkert vet om den finns.
Om man vill veta hur stor en energimängd är och när den har denna storlek måste
man göra en nogrann mätning under kort tid.Men ju noggrannare man vill veta
hur stor den är ju längre tid tar mätningen.Och ju mer exakt man vill veta
mättidpunkten ju sämre hinner man mäta energiinnehållet.
Heisenberg konstaterade att om man samtidigt försöker mäta två storheter A och B
som har egenskapen att deras produkt har sorten Js så blir minsta möjliga fel
ΔA ΔB = h/2
där h = Plancks konstant.
Energi
======
Enhetshändelser inträffar och bildar mönster i form av händelsekedjor.Sådana
händelsekedjor kallar vi händelser.Händelser inträffar hela tiden.Dessa
händelser är helt enkelt tiden.
Av alla händelser som inträffar är det en mycket liten del som vi kan
förutse och påverka.Men hur liten den delen än är är den viktig för oss.Så
viktig att vi behöver ett särskilt begrepp för den.Vi kallar förutsebara,
påverkbara händelser för energi.
Det förefaller som om vi inte kan tömma eller fylla en enstaka enhetscell.
Vi kan alltså inte göra om en etta till en nolla eller tvärtom.Däremot kan
ettor byta plats med nollor.Så vitt vi vet består alla händelser vi observerar
i att ettor och nollor byter plats.Världens BIOS tycks se till att minnet hela
tiden har lika många ettor.
Nollor är mycket vanligare än ettor i vår värld.Om vi påträffar en fylld
enhetscell,d v s en etta,kan vi alltså förutse att den kommer att bytas ut mot
en nolla.De ettor vi observerar är alltså förutsägbara förändringar d v s
förutsägbara och därmed påverkbara händelser,d v s energi.
Den tätaste materia vi känner är den som finns i kollapsade stjärnor.Om vi
antar att denna materia består av enbart ettor kan vi uppskatta andelen ettor
i vår del av världen.En uppskattning av denna täthet är 3 1010 kg/m3.
Medeltätheten i vår del av världen rör sig om 4 10-26 kg/m3.
Förhållandet mellan dessa tätheter utgör ett mått på andelen ettor i vår värld.
Det går alltså c:a 1036 nollor på varje etta.
Även i den tätaste materia vi känner här på jorden går det mer än en miljon
nollor på varje etta.
En enhetshändelse innebär alltså att en etta och en nolla byter plats.Eftersom
antalet ettor är så mycket mindre än antalet nollor är det antalet ettor som
anger hur ofta detta sker.Antalet ettor inom en viss volym anger alltså hur
många förutsebara händelser som kommer att inträffa i volymen d v s hur stor
energi som finns i volymen.
Om man kan avgränsa en viss volym så att den inte kan utbyta ettor mot nollor
eller tvärsom över volymgränsen blir antalet ettor d v s energin konstant inom
volymen.
Detta brukar kallas för termodynamikens första huvudsats och formuleras som att
energin hos ett slutet system är alltid konstant.
Men en enhetshändelse är mycket liten,så liten att vi inte känner något sätt att
utnyttja en enstaka enhetshändelse.Att försöka finna en enstaka etta för att
kunna utnyttja att vi kan förutse att den kommer att bytas ut mot en nolla är
som att försöka manipulera gener med grävskopa.Våra sinnen,instrument och verktyg
är trubbiga och vi behöver enhetshändelser som sker samordnat till användbara
händelser.Om vi avgränsar en viss volym så att den bildar ett slutet system
kan det hända att fördelningen av ettor inom systemet är ojämn.Vi kan t ex
ha många fler ettor i ett hörn än i resten av volymen.Vi kan då,inte bara förutse
att varje etta kommer att bytas mot en nolla,vi kan förutse att sådana byten
kommer att ske oftare i detta hörn än i resten av volymen.Och detta kan ske i
en skala som vi kan använda.En sned fördelning av ettor inom ett slutet
system kan vi alltså använda.Men det är användbart därför att vi kan förutse
att fördelningen kommer att utjämnas och när vi använder det utjämnas för-
delningen och blir oanvändbar.
Detta brukar kallas för termodynamikens andra huvudsats.Den formulerades i en
tid när man främst var intresserad av att omvandla värme till arbete och när man
fann att man måste ha en sned temperaturfördelning för att omvandla värme till
arbete.Den brukar därför formuleras:Entropin (värmelärans motsvarighet till
ellärans laddning eller mekanikens tyngd) hos ett slutet system kan inte
minska.
En konsekvens av andra huvudsatsen är att tiden bara går åt ett håll.I stället
för att säga "Entropin hos ett slutet system kan inte minska" skulle vi kunna
säga "Tiden kan inte minska".
När vi var små spelade min bror och jag ibland schack.Det hände att vi hamnade
i lägen där vi inte kunde komma på vad vi skulle göra härnäst.Jag kunde då
flytta tornet ett steg för att i nästa drag återgå till utgångsläget och han
kunde göra likadant.Så kunde vi "spela" hur länge som helst utan att ställningen
förändrades.Spelet gick bara framåt av irreversibla drag t ex flyttning av en
bonde,att någon slog en pjäs eller att någon gjorde ett drag som öppnade nya
möjligheter.
Om en etta byter plats med en nolla går tiden fram en enhet.Men om nästa
enhetshändelse är att ettan återgår till utgångsläget går tiden bakåt en
enhet.Ingen kan veta att något har hänt.Alla minnen består av enhetsceller
och för att någon skall kunna minnas en händelse måste den orsaka en
händelsekedja som ställer om något minne.
Liksom schackspelet går tiden bara framåt av händelser som är eller som på
grund av andra händelser blir irreversibla.
När man började studera möjligheter att omvandla värme till arbete fann man
att man vanligen utgick från värme med hög temperatur och liten entropi för
att sluta med en rest av värme vid omgivningstemperatur med högre entropi
än utgångsvärmet.Entropiökningen innebar att man inte kunde komma
tillbaka till utgångsläget. Man började därför betrakta entropi som ett mått
på irreversibilitet.Och begreppet används idag i vidgad betydelse så att
man t ex vid kemiska reaktioner talar om en entropiterm som anger
reaktionens grad av irreversibilitet även om det inte direkt är fråga om
en omvandling till värme.
Med denna vidgning av begreppet blir alltså entropiökning en synonym till
tidökning.Och andra huvudsatsen utsäger det vi alla av erfarenhet vet,
nämligen att tiden bara går åt ett håll.
Termodynamikens första och andra huvudsatser är viktiga regler som vi kan
använda när vi försöker utnyttjas världens BIOS.Men utöver dem finns det andra
hinder för utjämning mellan ettor och nollor.Möjligheten att avgränsa slutna
system innebär att det finns möjligheter att "låsa in" ettor i avgränsade
volymer där utjämning med omgivningen inte sker trots att den borde göra det
enligt första och andra huvudsatsen.Vi har t ex inte funnit något sätt
att få materia att restlöst omvandla sig till andra energiformer trots
att första och andra huvudsatsen säger att det borde vara möjligt.
Arbete
======
Antag att jag skall lyfta en säck mjöl.
Jag skall då genomföra den procedur som inom datatekniken kallas för shift.
Via världens BIOS anropar jag shift-proceduren för alla de bits som utgör
säcken.Detta anrop omfattar en lång och komplicerad händelsekedja men på
samma sätt som en dators operativsystem gömmer programelement för operatören
är denna kedja okänd för mig.Jag vet bara att jag anropar shift-proceduren
genom att ta tag i säcken och lyfta.
När alla de bits som utgör säcken skiftats mot ovanförliggande bits har säcken
lyfts en enhetslängd och det är bara att anropa shift-proceduren på nytt och
på nytt tills jag fått upp den tillräckligt.
Jag finner nu att det krävs en viss viljeansträngning för att jag,på detta
sätt,skall anropa shift-proceduren.Utförande av något som kräver viljeansträng-
ning kallar vi arbete.Här på jorden är det tydligen så att det krävs arbete
för att lyfta föremål.Att lyfta är en typ av förflyttning och jag finner att
även andra typer av föremålsförflyttning kan kräva arbete.Inom fysik gör man
den förenklingen att man enbart talar om sådant arbete som är knutet till
förflyttning av föremål.
Om jag provar att lyfta olika säckar till olika höjd finner jag att det krävs
mer arbete att lyfta en säck ju högre jag lyfter den och det krävs mer arbete
ju mer det är i den.Åker jag till månen finner jag också att det krävs mer
arbete att lyfta en viss säck till en viss höjd på jorden än på månen.
Shift-proceduren innebär ju en förutsägbar och avsiktlig förändring.Den är
alltså energi.Arbete i fysikalisk mening är alltså en form av energi.Men även
om det krävs lika mycket energi,d v s arbete,för att lyfta en lätt säck till
hög höjd som att lyfta en tung säck till låg höjd är dessa procedurer olika
och vi behöver metoder att beskriva dem som visar hur de skiljer sig från
varandra.
Vi gör då en uppdelning i
Antal ettor som skall skiftas
En faktor som anger hur svårt det är att skifta på den plats man är
Antal shift-procedurer som krävs
Vi säger att
W = mg h
där
W = det arbete,d v s den energi,som krävs för lyftet (Work)
m = säckens massa d v s antalet ettor som ingår i säcken
g = gravitationskonstanten som är olika på jorden och på månen
h = lyfthöjden,d v s antal erforderliga shift-procedurer
Produkten mg kallar vi säckens tyngd.
Vi delar alltså upp energin i två faktorer där den ena (tyngden) anger hur stor
mängd vi arbetar med.Vi kallar denna faktor för extensiv faktor eller mängdfaktor.
Den andra faktorn anger hur stor förändring varje del av mängden utsätts för.Vi
kallar den faktorn för intensiv faktor.
För min mjölsäck är alltså tyngden (mg) extensiv faktor och lyfthöjden (h)
intensiv faktor.
Kraft
=====
Vi säger att mjölsäckens tyngd är en kraft.För att åstadkomma denna anropar
jag shift-proceduren via världens BIOS.Men jag finner att jag behöver göra
likadana anrop i en rad andra fall.Om jag skall dra ett föremål över ett
strävt underlag,om jag skall sätta fart på en sten för att kasta den,om
jag skall dra en båt i vatten måste jag göra likadana proceduranrop.Vi
kallar alla sådana anrop för kraft oavsett om vi åstadkommer dem själva
eller om vi utnyttjar någon maskin för att göra dem.
Att anbringa en kraft på ett föremål är en uppmaning till föremålet att
förflytta sig.Om det förflyttar sig sker en förändring d v s energi omsätts.
Kraften gånger förflyttningslängden är den omsatta energin.
För att kunna räkna med krafter behöver vi något hanterligt mått på dem.
Vi använder oss då av den regel i världens BIOS som säger att om ingenting
bromsar rörelsen kommer en kraft som verkar på en massa att öka dess hastighet.
Vi kallar den kraft som varje sekund ökar hastigheten hos en massa på 1 kg med
1 m/s för 1 N (Newton).Vi har alltså att
1 N = 1 kg m/s2
Vi använder oss av krafter för att åstadkomma önskade förändringar där och när
vi vill ha dem.Men förändringar inträffar också hela tiden spontant.Om vi vill
åka med ett luftskepp från Stockholm till Göteborg startar vi en drivmotor som
ger en kraft som förflyttar skeppet mot Göteborg.Denna kraft gånger den väg vi
färdas är det arbete,d v s den energi,som vi måste tillföra.Men det är viktigt
att observera att denna energitillförsel inte är nödvändig för att vi skall
komma till Göteborg i och för sig.Den är nödvändig för att vi skall kunna
förutsäga när vi kommer till Göteborg.Om vi lät skeppet driva omkring i luft-
havet i oändlig tid skulle vi naturligtvis,förr eller senare,hamna över
Göteborg och då skulle vi alltså ha fullbordat resan.Men det är ett mycket
opraktiskt sätt att resa.Vi behöver åtminstone någon typ av kraft som gör att
vi kan förutsäga färdvägen lite bättre.
Brus
====
Värme är slumpmässiga molekylrörelser (eller strålningsvärme). I en gas far
molekylerna omkring samtidigt som de roterar. I ett fast ämne vibrerar
molekylerna kring sina jämviktslägen.
Om man, med allt större noggrannhet försöker bestämma läget hos ytan av ett
stycke fast materia kommer man så småningom till problemet att det inte går
att komma längre därför att de atomer som utgör ytan hela tiden rör sig.
Om man observerar en liten partikel som svävar i en vätska finner man att
den rör sig med knyckiga slumpmässiga rörelser (Browns rörelse) som beror
på kollisioner med vätskemolekyler.
Kollisioner kan även medföra att elektroner slås ut från sina lägen i
elektronskalen vilket ger en slumpmässigt varierande spänning, d v s ett
elektroniskt brus.
När man i teleteknikens barndom försökte signalera över allt större avstånd
genom att förstärka den mottagna signalen med allt högre förstärkning fann
man att man inte bara förstärkte signalen utan också ett brus. Och när
signalen drunknade i bruset kunde man inte komma längre genom att öka
förstärkningen.
Slumpmässiga, d v s oförutsägbara, händelser inträffar. Det är bara en liten
del av alla händelser som är förutsägbara genom att de har en känd orsak.
Även när det finns en känd orsak kan det finnas oförutsägbarhet om detaljer i
verkan. Värme är en orsak till molekylrörelse men hastighet och riktning för
en enskild molekyl är oförutsägbar.
Temperatur är ett mått på variansen på molekylhastigheten. Om variansen är
skiljd från noll kan vi förutsäga att en viss molekyl kommer att röra sig men
det säger ingenting om åt vilket håll och det ger bara en antydan om hur
fort den kommer att röra sig.
För en ideal gas gäller
m s2 = 3 k T
där
m molekylens massa i kg
s2 variansen på den slumpmässiga molekylhastigheten
k Boltzmanns konstant
T absoluta temperaturen i K
Styrkan hos en signal avtar med avståndet (i tid och/eller rum) från orsaken.
Bruset beror på temperaturen hos bakgrunden och temperaturen hos mottagaren.
Med ökande avstånd kommer således signalen så småningom att drunkna i bruset.
Våra förutsägelser blir alltså alltmer osäkra.
Vi kan t ex göra väderprognoser baserade på dagens kända orsaker till väder-
förändringar men bruset genererar hela tiden oförutsägbara orsaker till
förändringar och allteftersom tiden går kommer dessa allt mer att dominera
över dagens kända orsaker.
Allt vi gör är alltså förgängligt. Vilken verkan vi än åstadkommer kommer den
så småningom att drunkna i de slumpmässiga förändringar som bruset orsakar.
Den fyrdimensionella världen
============================
Med avståndet mellan punkterna A och B menar vi det minsta antal enhetsceller
man måste passera för att komma från A till B.På liknande sätt kan man
definiera tidsavståndet mellan händelserna a och b som det antal enhetshändelser
som inträffar mellan a och b.
Ett sätt att hantera avstånd mellan ett stort antal punkter är att lägga in dem
i ett treaxligt koordinatsystem.I stället för att ange alla möjliga avstånd kan
vi då ange alla punkters koordinater och ur dessa beräkna de avstånd vi vill
veta.
Det ligger nära till hands att lägga till en koordinataxel och använda den för
att ange tidskoordinat.Med avstånd i ett sådant fyraxligt koordinatsystem menar
vi då,inte bara antal enhetsceller mellan A och B utan också antal enhetshändelser
mellan att vi utgår från A och kommer fram till B.
Om vi använder ett sådant fyraxligt koordinatsystem kan vi ge tid två olika
betydelser.Vi kan dels tala om tid som en förändringsparameter.Vi kan kalla
detta för parametertid.Och vi kan tala om tid som en lägeskoordinat i vår
fyrdimensionella värld.
Så kan vi naturligtvis göra men normalt växer parametertiden och koordinattiden
likadant.Finns det då någon anledning att skilja på begreppen?Finns det något
i världens BIOS som går att beskriva genom att vi skiljer på begreppen?
Världens BIOS uppför sig faktiskt som om det fanns något som strömmade med viss
hastighet åt något håll i den fyrdimensionella rymden.Vi har inget bra namn på
detta något.Det har kallats världseter eller Brahma men låt oss för enkelhets
skull kalla det för eter.
Om allt står stilla i rummet strömmar etern i tidsriktning.Och hastigheten blir
c = t/τ
där
c = eterns strömningshastighet d v s ljushastigheten
t = koordinattid
τ = parametertid
Allt står då stilla i rummet och följer med en eter som strömmar i tidsled.
Om något rör sig i rummet kan vi uppfatta detta som att hastigheten där ändrar
riktning.Om något föremål flyttar sig sträckan s på parametertiden τ säger vi
att det rör sig med hastigheten v enligt
v = s/τ = c sin(α)
där
α = vridningsvinkeln för föremålets hastighetsvektor
Man kan uppfatta ljus som en ström av partiklar,fotoner,som rör sig med ljus-
hastighet i rummet.Fotonernas hastighetsvektor har alltså vridits 90 grader så
att de rör sig i rummet men står stilla i tiden.
Om man,likt Munchhausen,kunde hoppa ombord på en foton och titta bakåt skulle
man se startplatsen sådan den såg ut när man startade.Alla klockor på startplatsen
skulle då stå stilla.Man skulle inte röra sig i startplatsens tidsled.Men man
skulle röra sig med ljushastighet i någon annan riktning som man själv skulle
uppfatta som tidsriktningen och de som var kvar på startplatsen skulle kalla en
rumsriktning.
Gravitation
===========
Betrakta två partiklar A och B på avståndet ab.
I fig 1 anger den blå ytan alla punkter som ligger närmare A än vad B gör.Och
den gula ytan anger punkter som ligger längre ifrån A än vad B gör.Om nu B
rör sig helt slumpmässigt i förhållande till A finns det uppenbarligen många
fler punkter dit B kan gå för att öka avståndet till A än punkter dit B kan
gå för att minska avståndet.
Fig 3
Man utgår från en förstärkare som förstärker insignalen e med råförstärkningen
F till utsignalen c. När man ökar förstärkningen växer c och därmed βc och
närmar sig r. Det medför att e minskar och går mot noll när F går mot
oändligheten. För höga värden på F gäller alltså att
r = β c
c = r/β
Om man t ex vill åstadkomma ett förstärkarsteg med förstärkningen 10 gånger gör
man en spänningsdelare som ger β = 0,1. Även om F varierar mellan t ex
10 000 och 1000 000 gånger kommer då c att vara praktiskt taget 10 r.
Men ovanstående resonemang förutsätter att signalen inte fördröjs innan den
jämförs med r. Om en sinusformad signal fördröjs med halva periodtiden byter
den tecken. Då blir inte felsignalen skillnaden mellan r och βc utan summan
av r och beloppet av βc. Ökande F medför då inte att e minskar. e kommer
i stället att öka Om β F > 1 kommer då c att gå mot oändligheten oavsett
vad r är. Förstärkaren ger alltså ifrån sig en signal som är så stor att
förstärkaren bottnar oberoende av vilken insignal den fått.
Anordningen blir alltså instabil om det finns en frekvens där signalen fördröjs
en halv period samtidigt som β F (den s k loopförstärkningen) är större än 1.
Vanligtvis blir födröjningen allt större del av periodtiden när frekvensen ökar,
d v s fasvridningen ökar med ökande frekvens.
Ökande frekvens brukar också medföra att förstärkningen minskar.
Om man konstruerar en förstärkare och en återföringsloop så att β F < 1 när
fasvridningen blir 180 grader får man alltså en stabil förstärkare.
Genom att ersätta tidsfunktionerna r , e , c , F och β med motsvarande
Laplacetransformer får vi en möjlighet att samtidigt hantera amplitud och
fördröjning. Metoden är teoretiskt elegant och i vissa sammanhang användbar
men den ställer ganska stora krav på att användaren behärskar övergången
mellan tidsfunktioner och Laplacetransformer.
Ett annat sätt att samtidigt hantera amplitud och fördröjning är att använda
komplexa tal. En signal kan delas upp i och beskrivas som en summa av
sinusformade signaler (Fourier-uppdelning). En beskrivning av hur en
förstärkare uppför sig för sinusformade signaler av olika frekvens ger
alltså en fullständig bild av hur förstärkaren uppför sig för godtyckliga
signaler. Man kan då använda komplexa tal där beloppet motsvarar
amplitud och argumentet motsvarar fasvridning. Man kan då i det
komplexa talplanet rita kurvor som visar hur förstärkningen blir vid
olika frekvenser. Om en sådan kurva omsluter punkten -1 + i0 är
förstärkaren instabil (Nyquist-kriteriet).
Ett annat sätt att formulera Nyquist-kriteriet är: Om förstärningen vid
någon frekvens ger fasvridningen 180 grader samtidigt som dess
belopp är större än 1 blir förstärkaren instabil.
Det går alltså att formulera villkor för stabilitet hos den återkopplade
förstärkaren och i många andra sammanhang kan man se att förhållandena
kan hanteras på samma sätt.
DEL 3
Hur fungerar världen?
=====================
Aristoteles (384 - 322 f Kr) gjorde en ganska omfattande sammanställning av
vad som då var känt.Han och hans efterföljare sa i princip:
Världen är vad den synes vara eller borde vara
Tunga föremål faller fortare än lätta.Stora hus är större än små och skall
alltså avbildas större.Solen och stjärnorna rör sig över himlen.Det finns
fyra aggregationstillstånd jord = fast fas , vatten = vätska , luft = gas ,
eld = plasma och kanske ett femte "de vises sten" = kollapsad stjärnmateria
och av dessa tillstånd är allt uppbyggt.
I stort sett stod sig denna uppfattning i ett och ett halvt årtusende.
Världen fungerade enligt av Gud givna lagar.Men Gud kunde bryta mot lagarna
och bistå enskilda människor.Och han var stor nog att bry sig om varje
människa.Det kunde löna sig att be om underverk,särskilt om man anlitade
prästerlig konsulthjälp.
Men tankebyggnaden började knaka i fogarna.Om man avbildade stora hus små
när de var långt borta blev bilderna mer lika verkligheten än när man
använde "korrekt" storlek.
Copernicus (1473 - 1543) visade att man fick en enklare bild av verkligheten
om man tänkte sig att jorden roterar kring sin axel och kring solen.
Galilei (1564 -1642) spädde på med att visa att man kunde se Jupiters månar
rotera kring planeten om man använde en kikare.Och han visade även att
påståendet att tunga föremål faller fortare än lätta bara gäller om de
lätta har större luftmotstånd i förhållande till sin vikt.
Påven, som såg hur fotfästet för hela världsuppfattningen höll på att gå
förlorat, försökte förgäves stoppa sådana ideer.
Newton (1642 -1727) visade att händelseförlopp kunde beräknas och förutses i
en utsträckning som man dittills inte kunnat tänka sig.Guds ingripanden
behövdes i långt mindre omfattning än vad man föreställt sig tidigare.En stor
del av förtröstan på Guds godhet kunde flyttas över på en förlitan på att
världen var förutsägbar.Gud hade skapat världen så att han mycket sällan
behövde ingripa. Världsuppfattningen fick ett nytt fotfäste.
För närobservationer använder vi känsel,hörsel,lukt,smak och syn men för fjärr-
observation är vi praktiskt taget helt hänvisade till synen.Kunskap om ljus
spelar därför en avgörande roll för vår världsuppfattning.Maxwell (1831 - 1879)
gav med den elektromagnetiska ljusteorin en mycket elegant beskrivning av ljus.
Men han väckte också en besvärlig fråga.
Maxwells ekvationer beskriver ljus som en vågrörelse mellan elektriskt och
magnetiskt fält.Men det finns ingen knytning av denna vågrörelse till ett
vågbärande medium. Vattenvågor bärs av vatten,ljudvågor bärs av luft och vi
kan definiera vågornas hastighet i förhållande till vattnet eller luften.
Och om vattnet eller luften strömmar påverkas även vågornas rörelse. Men
Maxwells ekvationer visade inte på något sådant för ljus!!
När Michelson (1852 - 1931) och Morley försökte mäta jordens hastighet
i förhållande till den ljusbärande världsetern blev resultatet noll.Liksom den
fasta jorden hade rubbats av Copernicus sviktade nu den fasta världsetern.
Einstein (1879 - 1955) hävdade att vi måste överge föreställningen att alla ser
samma värld.Om två observatörer rör sig i förhållande till varandra upplever de
att den andres klocka och meterstav påverkas av rörelsen.
Heisenberg (1901 - 1976) visade att vi inte samtidigt kan mäta tid och energi
med hur stor noggrannhet som helst.Och mätningarna påverkar vad vi mäter.Trots
att vi kommit på hur man kan bygga förstärkare som förstärker en signal till
vilken styrka som helst finns det gränser för hur noggrant man kan mäta.
Fotfästet i en av Gud given värld som är oberoende av alla observatörer sviktade.
Men om vi delar upp tidsbegreppet i koordinattid och parametertid där
koordinattid är en rumskoordinat likvärd de övriga tre och parametertiden är
en förändringsparameter då kanske vi åter kan se en eter,ett alluppfyllande
Brahma.Ett Brahma som strömmar med ljushastighet som en etervind. En etervind
som vi svävar i som ballonger eller moln som följer vinden. En vind som kan
blåsa åt olika håll i det tredimensionella rummet genom att etern är
kompressibel och/eller att etervinden i koordinattidsled kan variera. En värld
som är lika för alla betraktare men där den tredimensionella projektionen av
den fyrdimensionella världen kan variera för olika betraktare.
Vad är verklighet?
==================
Vi lever i en värld som förändras.Denna värld observerar vi med
sinnen som registrerar förändringar.
Om man sätter ett finger mot en bordsyta känner man när fingret
vidrör bordsytan.Men om man håller kvar fingret försvinner
känslan.Vårt känselsinne registrerar alltså inte kontakten med
bordsytan utan bara förändringen när fingret sätts mot bordet.
Om man håller ögonen orörliga under tillräckligt lång tid för-
svinner synintrycket.För att vi skall se något räcker det inte
med förändringarna när enskilda fotoner träffar näthinnan.Hela
mönstret i bilden måste förändras för att vi skall se något.
Vi ser inte världen sådan den är.Vi ser förändringar av världen.
Det vi upplever som verklighet är alltså inte verkligheten utan
förändringen av verkligheten.Vi ser inte verkligheten utan verk-
lighetens tidsderivata.
Bakom den verklighet vi upplever när våra sinnen registrerar
förändringar finns alltså en verklighet som förändras.
Ett föremål som ett hus kan förefalla vara en stabil oföränder-
lig företeelse men för att vi skall kunna veta att det finns
måste det förändra ljusstrålar som faller på det eller stoppa upp
vår handrörelse när vi tar på det.Våra sinnen registrerar alltså
enbart förändringar runt huset.Vi kan bara indirekt sluta oss
till att huset finns.
Våra sinnen informerar oss om förändringar i vår omvärld och vi
finner att många av dessa kan beskrivas genom att vi antar att
det finns en bakomliggande verklighet som orsakar dessa föränd-
ringar.Utifrån de förändringar vi registrerar kan vi dra vissa
slutsatser om denna verklighet men vi kan inte få veta allt om
den.
Om världen kan beskrivas av någon sorts funktion som har en tids-
derivata och om vi kan registrera tidsderivatan kan vi integrera
denna tidsderivata för att komma till ursprungsfunktionen.Men vi
vet att integration ger en obestämd integrationskonstant.Tids-
derivatan innehåller alltså inte all information om ursprungs-
funktionen.
Den värld vi upplever med våra sinnen är alltså förändringar av
en bakomliggande verklighet.Och för de flesta av oss gäller att
all vår strävan går ut på att styra dessa förändringar och
därigenom anpassa världen efter våra önskemål.
För att vi skall kunna uppfatta något måste världen innehålla
företeelser som avviker från omgivningen (kvanta) och dessa måste
bilda händelser genom att ändra läge i förhållande till varandra.
Vi kan inte se kvanta bara händelser.
För att observera något måste vi förändra det vi observerar. Det
är bara genom att se hur det förändras som vi kan dra slutsatser om
hur det ser ut. Vi kan inte komma fram till "das Ding an sich", till
verkligheten sådan den är. Vi kan bara föreställa oss en verklighet
som förändras på det sätt som vi observerar.
Ju noggrannare vi mäter ju mer förändrar vi det vi mäter. Om vi vill
veta allt om hur stenarna ligger i ett tegelhus måste vi plocka bort
alla stenar och förändra huset till en tegelstenshög. Men så brukar
vi inte göra. Vi nöjer oss med att se ytan på ytliga stenar och
kanske plocka bort ett par stycken. Så antar vi att övriga stenar
ligger på samma sätt, d v s att mönstret upprepas. Det mesta av vår
världsuppfattning bygger på denna föreställning om mönsterupprepning.
Vi föreställer oss en värld där mönster upprepas som tapetmönster. En
värld där förändringar kan inträffa och bilda händelser som vi kan
registrera med våra sinnen så att vi kan dra slutsatser om hur mönstren
ser ut.
Denna mönsterupprepning är ett av de största mysterierna. Vi vet inte
varför det är så och mycket lite om de regler som den följer.
Plancks konstant - Alltets konstant
===================================
Betrakta ett universum som innehåller h stycken urskiljbara kvanta. Varje
sådant kvanta är så litet att det inte går att dela. Det kan bara finnas
eller inte finnas. Vi kan kalla ett sådant kvanta för enhetskvanta eller
på engelska unit-quanta och beteckna det med UQ. Sorten för h blir alltså UQ
Den minsta händelse som kan inträffa i detta universum är minsta detekterbara
lägesförändring för ett enhetskvanta i förhållande till övriga kvanta. En
sådan händelse kan vi kalla för enhetshändelse eller på engelska unit-event
och beteckna med UE.
Alla händelser kan delas upp i enhetshändelser men en enhetshändelse kan inte
delas upp. Den 'inträffar' eller 'inträffar icke'. Något däremellan finns inte.
Totala antalet enhetshändelser som någonsin inträffat i vårt universum kallas
för absolut tid ( egentligen absolut parametertid). Tidpunkten för en viss
händelse är totala antalet enhetshändelser som inträffat före händelsen.
Tiden mellan händelse A och händelse B är tidpunkten för händelse B minus
tidpunkten för händelse A. Tid betecknas med τ och sorten för tid blir
alltså UE.
Antag att vi intresserar oss för en viss del av vårt universum, t ex av en
kula. Av alla kvanta i universumet avgränsar vi då några som utgör kulan. Vi
kan beteckna dessa kvanta med E. Med E menar vi alltså ett visst antal
enhetskvanta och sorten för E blir alltså UQ. Då gäller att E/h anger hur
stor del av universum som kulan utgör.
Om det så inträffar en enhetshändelse är sannolikheten E/h att denna
enhetshändelse består i att något av de kvanta som utgör kulan ändrar läge.
På tiden τ inträffar τ enhetshändelser och varje gång är sannolikheten
E/h att något av de kvanta som utgör kulan ändrar läge. I uttrycket
τ E
a = -----
h
är alltså a det antal gånger som ett enhetskvanta som ingår i E ändrar läge
under tiden τ. Om man minskar τ och/eller E så att a blir mindre än ett
övergår a till att ange sannolikheten att något kvanta inom E ändrar läge under
tiden τ.
τ E UE UQ
Sorten för a = ----- blir ----------- d v s UE.
h UQ
Om vi avgränsar en så liten mängd kvanta ΔE och observerar den under så kort
tid Δτ att Δτ ΔE = h/2 kommer endast en halv enhetshändelse att
beröra ΔE d v s sannolikheten att någon händelse inträffar som berör ΔE blir
0,5. Detta är gränsen för att vi skall kunna se att något händer med ΔE.
(Heisenbergs osäkerhetsrelation).
Låt oss se på ett litet universum med h = 1000 UQ där vi avgränsar en kula
med E = 10 UQ. Det är då bara var hundrade UQ som tillhör E. Det är alltså
bara var hundrade enhetshändelse som innebär att något kvanta i E har
flyttats. Efter en förändring av E går det alltså 100 UE innan det på nytt
är dags för en förändring av E. Vi säger att E:s periodtid är 100 UE.
Periodtid betecknas T och har sorten UE. För att bestämma periodtiden
sätter vi a = 1 i uttrycket τ = a h/E och får alltså T = h/E. Egentligen
är alltså T = 1 h/E där 1 har sorten UE så att även T får sorten UE.
Inverterade värdet av periodtiden kallas för frekvens.
Frekvens betecknas f och har sorten UE-1. Frekvensen för E är
f = E/h alltså egentligen f = E/(1 h) där ettan har sorten UE.
h är alltså antalet enhetskvanta i hela universum. Sorten för h är alltså UQ.
Men h är också det antal enhetshändelser som erfordras för att rubba samtliga
enhetskvanta i universum. Ser vi det så har h sorten UE. Och om en viss
enhetshändelse inträffar är h det antal enhetshändelser som troligen inträffar
innan den upprepas. Även om vi ser h på det viset blir sorten UE.
Även om alltså sorten för h inte är helt entydig är värdet entydigt för ett
visst universum. För alla i vårt universum har h samma värde. Men trots det
har vi ingen bra metod att fastställa detta värde. Vi vet inte exakt hur stort
vårt universum är och därmed vet vi inte heller det exakta värdet på h. Vi har
alltså inget bra värde på h varken i sorten UQ eller UE. Om vi vill kan vi
emellertid vända på resonemanget och säga att vi mycket väl vet värdet på h
men vi vet inte hur stort ett enhetskvanta är och därför kan vi inte uttrycka
h i sorten UQ.
Vi använder inte enheterna UQ ch UE för att ange kvantamängder och tider.
Detta beror dels på att det skulle bli svårhanterligt stora tal dels på att
vi inte exakt kan fastställa storleken på ett UQ och på en UE. Vi använder
i stället sorter som Joule och sekund som är ett stort antal UQ resp UE.
På en sekund går det ett visst antal (ks) enhetshändelser. På en
Joule går det ett visst antal (kJ) enhetskvanta. För att avgöra
vad som händer med värdet på h om vi övergår till att ange τ i sekunder
och E i Joule kan vi utgå från uttrycket τ E = a h. Om vi övergår till
sekunder och Joule får vi
τ ks E kJ = a h
a h
τ E = --- ---
ks kJ
Vi bibehåller sorten UE för a och får då
h i Js lika med (h i UQ)/(ks kJ)
Sorten för h är inte entydig eftersom ett enhetskvanta under vissa
omständigheter motsvaras av en enhetshändelse. h får då samma värde
oberoende av om vi använder sorten UQ eller UE. Men använder vi i
stället sekund och Joule måste omräkningsfaktorerna komma på rätt
plats och vi får då entydigt sorten Js för h.
h kallas för Plancks konstant.
Bortom tid och rum
==================
När vi som barn blir medvetna om vår omgivning börjar vi fråga "Vad
finns bortom?" , "Vad fanns före?" och "Vad kommer efter?".Och varje
gång vi får ett svar förskjuter vi gränserna för den värld vi upplever
som känd och ställer på nytt samma frågor.
Till slut brukar vi bli avspisade med att frågorna är meningslösa och
att ingen kan svara på dem.Men så är det faktiskt inte.Vi kan faktiskt
ibland hitta absoluta gränser.Det kanske mest iögonfallande exemplet är
absoluta nollpunkten för temperatur.
När man upptäckte att gaser ökade tryck och/eller volym när man värmde
dem fick man ett sätt att mäta temperatur.Vår instinkt att fråga "Vad
finns bortom?" ledde till att man började fundera kring frågan "Hur
kallt kan det bli?".Och svaret var faktiskt inte "Hur kallt som helst".
Om man kylde en gas vid konstant tryck minskade dess volym.Men till slut
kom man till volymen noll.Och eftersom vi inte kan tänka oss vad negativ
volym skulle kunna vara insåg man att det finns en absolut nollpunkt för
temperatur.
När vi tittar på en avlägsen stjärna tittar vi inte bara långt bort, vi
tittar även bakåt i tid.Vi ser inte stjärnan sådan den ser ut nu utan
sådan den såg ut när ljuset lämnade den. Om solen plötsligt slocknade
skulle vi inte märka något förrän det gått 8 minuter. Fram till dess
skulle ljus som var på väg mot oss när den slocknade fortsätta att komma
fram. Vi ser alltså inte solen sådan den är utan solen för 8 minuter
sedan.Och avlägsna stjärnor kan vi se för miljarder år sedan.
Liksom man en gång i tiden undrade hur kallt det kunde bli kan vi fråga oss
hur långt och hur långt tillbaka vi kan se. Och även här är faktiskt inte
svaret "Hur långt som helst".
Ljus kan uppfattas som en vågrörelse och färger som frekvensen hos denna
vågrörelse. Blått ljus har hög frekvens och rött ljus har lägre frekvens.
Vitt ljus är en blandning av olika färger d v s av olika frekvenser men
blandningen är inte jämn. Frekvenserna är koncentrerade till s k
spektrallinjer som motsvarar egenskaper hos de ämnen som avgivit ljuset.
Spiller man lite saltvatten i lågan på en gasspis lyser lågan med en gul
färg som motsvarar en kraftig spektrallinje hos det natrium som ingår i
saltet.
När vi tittar på ljus från fjärran stjärnor finner vi att färgen har
förskjutits mot rött. Och det är inte fråga om en omfördelning av
färgintensiteter för alla spektrallinjer har fått lägre frekvens. Det är
alltså så att ljusets frekvens blir lägre ju längre bort vi tittar.
Det innebär att om vi tittar tillräckligt långt bort blir ljusets frekvens
noll.
Och liksom vi inte kan tänka oss en negativ volym kan vi inte tänka oss en
negativ frekvens. Vi kan alltså inte ha större avstånd än att ljuset som når
oss från det avståndet får frekvensen noll. Och vi kan inte ha längre tid
tillbaka än gångtiden för ljus som når oss från detta avstånd.
Hur ser då världen ut när vi kommer till största möjliga avstånd? Vi "ser"
där en värld som avger ljus med frekvensen noll d v s totalt mörker. En
värld där vi inte kan urskilja någonting. Där vi inte kan skilja två punkter
från varandra och alltså inte tala om deras läge och avstånd. En värld där
vi inte kan urskilja punkter så att vi kan säga att en händelse har inträffat
genom att deras läge har förändrats. En värld utan avstånd och utan händelser
d v s en värld utan rum och tid.
Man brukar uppskatta det största möjliga avståndet till mellan 10 och 20
miljarder ljusår och motsvarande tid blir alltså mellan 10 och 20 miljarder
år.
Rum och tid är alltså ändliga begrepp som endast har mening lokalt i den
värld där vi råkar befinna oss. Utanför denna världs rum och tid råder en
jämn fördelning, d v s ett totalt mörker där allt överallt är lika. Vi
kommer ur ett totalt mörker, vi går mot ett totalt mörker och vi omges
av ett totalt mörker. Men den störning av detta perfekta tillstånd som
vi kallar världen är tillräckligt stor för att vi skall kunna ha en hel
del skoj på vägen.
Tid
===
En stillastående värld är ointressant.
Det finns en gammal film,jag tror den hette "A kind of stopwatch" om en man med
ett stoppur som har den egenskapen att när han startar det stannar allt i hela
världen utom han själv.Han använder det för att plundra en bank där han i lugn
och ro kan gå omkring bland stillastående kunder och tjänstemän.Men när han skall
trycka igång världen igen tappar han uret i golvet så att det går sönder och han
blir fast i en meningslös stillastående värld.
Lyckligtvis står vår värld inte stilla.Den är stadd i ständig förändring.
För att få ett mått på världens förändring kan vi dela in den och se den som
summan av en massa små händelser.
Den minsta händelse vi kan observera innebär att någon urskiljbar punkt
förändrar sitt läge i förhållande till övriga urskiljbara punkter med den
minsta detekterbara lägesförändringen.Vi kan kalla en sådan händelse för
en enhetshändelse.Så kan vi dela in världens förändring i enhetshändelser
(det blir ett stort och ohanterligt tal men det blir ett ändligt tal).
Enligt föregående avsnitt kan vi finna en gräns för hur långt tillbaka vi
kan gå och vi kan alltså finna en siffra som anger totala antalet
enhetshändelser sominträffat i vår värld.Siffran blir stor och vi har inte
mätmetoder som gör att vi kan bestämma den särskilt noggrant men vi kan
konstatera att denna siffra finns och vi kan kalla den för "absolut tid".
Vi kan uppskatta den absoluta tiden till att nu vara c:a 15 10120
enhetshändelser.
Det finns en mängd olika uppskattningar av Hubble-konstanten men låt oss
anta att universums ålder är 15 miljarder år och radien 15 miljarder ljusår.
Medeltätheten kan uppskattas till 4 10-26 kg/m3. Vilket innebär att
totala innehållet är 2 1053 kg eller 2 1070 J.Om vi dividerar med Plancks
konstant får vi motsvarande frekvens som alltså blir 3 10103 Hz.
Inverterar vi det värdet får vi periodtiden som vi kan använda som mått på
kortast möjliga tid d v s som mått på den tid som åtgår för en enhetshändelse.
Vi får alltså fram att det går 3 10103 enhetshändelser på en sekund och
att en enhetshändelse tar 3 10-104 s.Då 15 miljarder år är 5 1017 s
innebär det att den absoluta tiden nu är c:a 15 10120 enhetshändelser
Men även om vi inte kan bestämma den absoluta tiden särskilt noggrant och även om
den absoluta tiden blir ohanterligt stor kan vi,med stor noggrannhet,mäta tiden
mellan två händelser som inträffar inom vårt observationsområde.
Av alla händelser som inträffar i universum är de allra flesta helt slumpmässiga.
Det är bara en mycket liten del som vi kan påverka.Men enhetshändelser har en
tendens att bilda mönster och samordnas till större händelser som vi kan
observera.Eftersom sådana inträffar helt slumpmässigt kan vi utgå från att om
vi nöjer oss med att observera en viss typ av händelse inom ett litet område så
får vi ett mått på totala antalet händelser.Vi kan t ex bygga ett pendelur och
räkna med att varje gång händelsen att pendeln fullbordat ett slag har inträffat
har det gått en sekund d v s har det inträffat 3 10103 enhetshändelser i hela
universum.Att den andel av det totala antalet händelser som vi mäter på detta sätt
är konstant kan vi övertyga oss om genom att göra två likadana klockor och se
om de går likadant.Vi finner då att om vi kan isolera dem från störande
inverkan utifrån går de nästan exakt lika.
Rum
===
På liknande sätt som vi kan definiera en enhetshändelse kan vi definiera en
enhetslängd.En enhetslängd är helt enkelt den sträcka ljuset hinner gå under en
enhetshändelse.
Vårt universum blir då ett rum i form av ett klot med radien 15 10120 enhetslängder.
Detta klot kan vi dela in i enhetsceller med en enhetslängd som sidlängd.Detta
klot rymmer alltså c:a 1 10364 enhetsceller.
Om vi även vill räkna in alla enhetsceller som någonsin funnits får vi betrakta
tid som en fjärde dimension.Vi får då ett fyrdimensionellt halvklot med c:a
1 10485 enhetsceller.
En enhetscell ligger på gränsen till att vara observerbar.Det går alltså inte att
urskilja några detaljer i den.Vi kan bara skilja mellan om den innehåller något eller
om den är tom.Vi kan alltså fullständigt beskriva den med en etta eller en nolla.
Världen är alltså ett "datorminne" som rymmer 10364 bits och som totalt
har hanterat 10485 bits.
Med "avstånd" mellan A och B menar vi det antal enhetsceller vi måste passera för att
komma från A till B.
Vi kan alltså se på världen som en dator med ett enormt minne.Men en dator är
praktiskt taget oanvändbar om den inte har ett operativsystem som gör att innehållet
i minnet ändras enligt vissa regler.Och även världen har sitt "operativsystem".Hur
detta fungerar är vad fysik egentligen handlar om.
Orsak och verkan
================
För att bli användbar behöver en dator något operativsystem med någon form av BIOS
(Basic In/Out System).Ännu mer fundamentalt är att man redan i processorns hårdvara
brukar lägga in vissa begränsningar av hur minnet kan förändras.Man brukar t ex
dela in minnet i grupper om 8 , 16 eller 32 bits som hanteras samtidigt.
För att kunna använda datorn måste vi komma fram till en förenklad uppfattning av
den,en uppfattning som är användbar och som kan rymmas inom vår tankeförmåga.Vi
börjar då med att bortse från ettor och nollor för att i stället se grupper av
bits som vi kallar bytes.
På liknande sätt finner vi att världen har ett "BIOS" som grupperar enhetsceller.
Sammanhängande grupper av enhetsceller kallar vi partiklar och vi finner att det
finns förvånansvärt stabila sådana.Av någon anledning förblir mönstret av ettor
och nollor inom en partikel ofta konstant även om partikeln ändrar läge i
förhållande till andra partiklar.
Ett sätt att se detta bevarande av mönster är att jämföra med ballonger i
byig vind. Dessa flyttas av vindbyar så att de ändrar läge i förhållande till
varandra men om ballongerna ligger tätt kommer inte en vindby att ändra det
inbördes läget för närliggande ballonger.
Även i tidsled grupperar världens "BIOS" enhetshändelser till händelsekedjor som
bildar urskiljbara mönster.Om vi vet vad som har hänt kan vi,i vissa fall,förutse
vad som kommer att hända.Om vi vet att en partikel har förflyttat sig i ett område
med enbart nollor kan vi förutse att den kommer att fortsätta förflyttningen.
Vi kallar den förflyttning som redan skett för orsak och den som vi förutser för
verkan.
Vi har funnit ett antal orsak-verkan-samband som vi kan använda som ett sorts
högnivåspråk för programering av världen.Om vi önskar en viss verkan men finner
att den är svår att uppnå kan vi leta bland dessa samband för att se om vi i
stället kan finna en orsak som är lätt att åstadkomma och som ger önskad verkan.
Eller en orsak som har en verkan som kan vara orsak till den önskade verkan.Eller
en orsak till en orsak till en orsak till verkan.
Människor har naturligtvis alltid använt sig av orsakskedjor för att nå sina mål.
Men till en början skedde detta huvudsakligen intuitivt.Att orsaka en spräckning
av ett flintstycke så att man får en användbar flintkniv är en konst som våra
förfäder utvecklade och förfinade.Man lärde sig orsakskedjorna men man
verbaliserade dem inte.Lärlingen lärde sig huvudsakligen genom att se och höra
mästarens slag och genom att själv slå med slagsten på flinta.
Kring mitten av det gångna årtusendet började en målmetveten strävan att
verbalisera orsak-verkan-samband.Detta lyckades över förväntan och så sent som
under adertonhundratalets slut trodde man på fullt allvar att varje verkan
kunde knytas till orsaker som i sin tur kunde knytas till orsaker.
Kvantfysiken och speciellt Heisenbergs osäkerhetsrelation bröt med denna
föreställning genom att hävda att ett orsak-verkan-samband säger att en orsak
innebär en viss sannolikhet för en viss verkan.Denna sannolikhet kan vara nära
ett men den är alltid mindre än ett.
Om man släpper en sten är sannolikheten stor att den faller nedåt.Men det finns
en liten,beräkningsbar,sannolikhet att den faller uppåt.Denna sannolikhet är
naturligtvis så liten att vi,för praktiskt bruk,kan strunta i den.Men att den
finns är principiellt viktigt för det innebär att världen kan komma med
överraskningar.
Heisenbergs osäkerhetsrelation bygger på insikten att världen både har partikel-
karaktär och vågkaraktär samtidigt.Men en våg måste observeras under åtminstone
större delen av periodtiden innan man kan veta att det verkligen rör sig om en
våg.En ansamling fyllda enhetsceller,d v s en ansamling ettor,kan bilda en
partikel.Ju fler ettor den innehåller ju högre säger vi att dess energi är.
Och när vi använder vågbeskrivning blir dess frekvens energin dividerad med
Plancks konstant.Ju högre energi den har ju högre frekvens och därmed kortare
periodtid har den.
Något förenklat kan man säga att Heisenberg påpekade att man måste observera
en energimängd under halva dess periodtid innan man säkert vet om den finns.
Om man vill veta hur stor en energimängd är och när den har denna storlek måste
man göra en nogrann mätning under kort tid.Men ju noggrannare man vill veta
hur stor den är ju längre tid tar mätningen.Och ju mer exakt man vill veta
mättidpunkten ju sämre hinner man mäta energiinnehållet.
Heisenberg konstaterade att om man samtidigt försöker mäta två storheter A och B
som har egenskapen att deras produkt har sorten Js så blir minsta möjliga fel
ΔA ΔB = h/2
där h = Plancks konstant.
Energi
======
Enhetshändelser inträffar och bildar mönster i form av händelsekedjor.Sådana
händelsekedjor kallar vi händelser.Händelser inträffar hela tiden.Dessa
händelser är helt enkelt tiden.
Av alla händelser som inträffar är det en mycket liten del som vi kan
förutse och påverka.Men hur liten den delen än är är den viktig för oss.Så
viktig att vi behöver ett särskilt begrepp för den.Vi kallar förutsebara,
påverkbara händelser för energi.
Det förefaller som om vi inte kan tömma eller fylla en enstaka enhetscell.
Vi kan alltså inte göra om en etta till en nolla eller tvärtom.Däremot kan
ettor byta plats med nollor.Så vitt vi vet består alla händelser vi observerar
i att ettor och nollor byter plats.Världens BIOS tycks se till att minnet hela
tiden har lika många ettor.
Nollor är mycket vanligare än ettor i vår värld.Om vi påträffar en fylld
enhetscell,d v s en etta,kan vi alltså förutse att den kommer att bytas ut mot
en nolla.De ettor vi observerar är alltså förutsägbara förändringar d v s
förutsägbara och därmed påverkbara händelser,d v s energi.
Den tätaste materia vi känner är den som finns i kollapsade stjärnor.Om vi
antar att denna materia består av enbart ettor kan vi uppskatta andelen ettor
i vår del av världen.En uppskattning av denna täthet är 3 1010 kg/m3.
Medeltätheten i vår del av världen rör sig om 4 10-26 kg/m3.
Förhållandet mellan dessa tätheter utgör ett mått på andelen ettor i vår värld.
Det går alltså c:a 1036 nollor på varje etta.
Även i den tätaste materia vi känner här på jorden går det mer än en miljon
nollor på varje etta.
En enhetshändelse innebär alltså att en etta och en nolla byter plats.Eftersom
antalet ettor är så mycket mindre än antalet nollor är det antalet ettor som
anger hur ofta detta sker.Antalet ettor inom en viss volym anger alltså hur
många förutsebara händelser som kommer att inträffa i volymen d v s hur stor
energi som finns i volymen.
Om man kan avgränsa en viss volym så att den inte kan utbyta ettor mot nollor
eller tvärsom över volymgränsen blir antalet ettor d v s energin konstant inom
volymen.
Detta brukar kallas för termodynamikens första huvudsats och formuleras som att
energin hos ett slutet system är alltid konstant.
Men en enhetshändelse är mycket liten,så liten att vi inte känner något sätt att
utnyttja en enstaka enhetshändelse.Att försöka finna en enstaka etta för att
kunna utnyttja att vi kan förutse att den kommer att bytas ut mot en nolla är
som att försöka manipulera gener med grävskopa.Våra sinnen,instrument och verktyg
är trubbiga och vi behöver enhetshändelser som sker samordnat till användbara
händelser.Om vi avgränsar en viss volym så att den bildar ett slutet system
kan det hända att fördelningen av ettor inom systemet är ojämn.Vi kan t ex
ha många fler ettor i ett hörn än i resten av volymen.Vi kan då,inte bara förutse
att varje etta kommer att bytas mot en nolla,vi kan förutse att sådana byten
kommer att ske oftare i detta hörn än i resten av volymen.Och detta kan ske i
en skala som vi kan använda.En sned fördelning av ettor inom ett slutet
system kan vi alltså använda.Men det är användbart därför att vi kan förutse
att fördelningen kommer att utjämnas och när vi använder det utjämnas för-
delningen och blir oanvändbar.
Detta brukar kallas för termodynamikens andra huvudsats.Den formulerades i en
tid när man främst var intresserad av att omvandla värme till arbete och när man
fann att man måste ha en sned temperaturfördelning för att omvandla värme till
arbete.Den brukar därför formuleras:Entropin (värmelärans motsvarighet till
ellärans laddning eller mekanikens tyngd) hos ett slutet system kan inte
minska.
En konsekvens av andra huvudsatsen är att tiden bara går åt ett håll.I stället
för att säga "Entropin hos ett slutet system kan inte minska" skulle vi kunna
säga "Tiden kan inte minska".
När vi var små spelade min bror och jag ibland schack.Det hände att vi hamnade
i lägen där vi inte kunde komma på vad vi skulle göra härnäst.Jag kunde då
flytta tornet ett steg för att i nästa drag återgå till utgångsläget och han
kunde göra likadant.Så kunde vi "spela" hur länge som helst utan att ställningen
förändrades.Spelet gick bara framåt av irreversibla drag t ex flyttning av en
bonde,att någon slog en pjäs eller att någon gjorde ett drag som öppnade nya
möjligheter.
Om en etta byter plats med en nolla går tiden fram en enhet.Men om nästa
enhetshändelse är att ettan återgår till utgångsläget går tiden bakåt en
enhet.Ingen kan veta att något har hänt.Alla minnen består av enhetsceller
och för att någon skall kunna minnas en händelse måste den orsaka en
händelsekedja som ställer om något minne.
Liksom schackspelet går tiden bara framåt av händelser som är eller som på
grund av andra händelser blir irreversibla.
När man började studera möjligheter att omvandla värme till arbete fann man
att man vanligen utgick från värme med hög temperatur och liten entropi för
att sluta med en rest av värme vid omgivningstemperatur med högre entropi
än utgångsvärmet.Entropiökningen innebar att man inte kunde komma
tillbaka till utgångsläget. Man började därför betrakta entropi som ett mått
på irreversibilitet.Och begreppet används idag i vidgad betydelse så att
man t ex vid kemiska reaktioner talar om en entropiterm som anger
reaktionens grad av irreversibilitet även om det inte direkt är fråga om
en omvandling till värme.
Med denna vidgning av begreppet blir alltså entropiökning en synonym till
tidökning.Och andra huvudsatsen utsäger det vi alla av erfarenhet vet,
nämligen att tiden bara går åt ett håll.
Termodynamikens första och andra huvudsatser är viktiga regler som vi kan
använda när vi försöker utnyttjas världens BIOS.Men utöver dem finns det andra
hinder för utjämning mellan ettor och nollor.Möjligheten att avgränsa slutna
system innebär att det finns möjligheter att "låsa in" ettor i avgränsade
volymer där utjämning med omgivningen inte sker trots att den borde göra det
enligt första och andra huvudsatsen.Vi har t ex inte funnit något sätt
att få materia att restlöst omvandla sig till andra energiformer trots
att första och andra huvudsatsen säger att det borde vara möjligt.
Arbete
======
Antag att jag skall lyfta en säck mjöl.
Jag skall då genomföra den procedur som inom datatekniken kallas för shift.
Via världens BIOS anropar jag shift-proceduren för alla de bits som utgör
säcken.Detta anrop omfattar en lång och komplicerad händelsekedja men på
samma sätt som en dators operativsystem gömmer programelement för operatören
är denna kedja okänd för mig.Jag vet bara att jag anropar shift-proceduren
genom att ta tag i säcken och lyfta.
När alla de bits som utgör säcken skiftats mot ovanförliggande bits har säcken
lyfts en enhetslängd och det är bara att anropa shift-proceduren på nytt och
på nytt tills jag fått upp den tillräckligt.
Jag finner nu att det krävs en viss viljeansträngning för att jag,på detta
sätt,skall anropa shift-proceduren.Utförande av något som kräver viljeansträng-
ning kallar vi arbete.Här på jorden är det tydligen så att det krävs arbete
för att lyfta föremål.Att lyfta är en typ av förflyttning och jag finner att
även andra typer av föremålsförflyttning kan kräva arbete.Inom fysik gör man
den förenklingen att man enbart talar om sådant arbete som är knutet till
förflyttning av föremål.
Om jag provar att lyfta olika säckar till olika höjd finner jag att det krävs
mer arbete att lyfta en säck ju högre jag lyfter den och det krävs mer arbete
ju mer det är i den.Åker jag till månen finner jag också att det krävs mer
arbete att lyfta en viss säck till en viss höjd på jorden än på månen.
Shift-proceduren innebär ju en förutsägbar och avsiktlig förändring.Den är
alltså energi.Arbete i fysikalisk mening är alltså en form av energi.Men även
om det krävs lika mycket energi,d v s arbete,för att lyfta en lätt säck till
hög höjd som att lyfta en tung säck till låg höjd är dessa procedurer olika
och vi behöver metoder att beskriva dem som visar hur de skiljer sig från
varandra.
Vi gör då en uppdelning i
Antal ettor som skall skiftas
En faktor som anger hur svårt det är att skifta på den plats man är
Antal shift-procedurer som krävs
Vi säger att
W = mg h
där
W = det arbete,d v s den energi,som krävs för lyftet (Work)
m = säckens massa d v s antalet ettor som ingår i säcken
g = gravitationskonstanten som är olika på jorden och på månen
h = lyfthöjden,d v s antal erforderliga shift-procedurer
Produkten mg kallar vi säckens tyngd.
Vi delar alltså upp energin i två faktorer där den ena (tyngden) anger hur stor
mängd vi arbetar med.Vi kallar denna faktor för extensiv faktor eller mängdfaktor.
Den andra faktorn anger hur stor förändring varje del av mängden utsätts för.Vi
kallar den faktorn för intensiv faktor.
För min mjölsäck är alltså tyngden (mg) extensiv faktor och lyfthöjden (h)
intensiv faktor.
Kraft
=====
Vi säger att mjölsäckens tyngd är en kraft.För att åstadkomma denna anropar
jag shift-proceduren via världens BIOS.Men jag finner att jag behöver göra
likadana anrop i en rad andra fall.Om jag skall dra ett föremål över ett
strävt underlag,om jag skall sätta fart på en sten för att kasta den,om
jag skall dra en båt i vatten måste jag göra likadana proceduranrop.Vi
kallar alla sådana anrop för kraft oavsett om vi åstadkommer dem själva
eller om vi utnyttjar någon maskin för att göra dem.
Att anbringa en kraft på ett föremål är en uppmaning till föremålet att
förflytta sig.Om det förflyttar sig sker en förändring d v s energi omsätts.
Kraften gånger förflyttningslängden är den omsatta energin.
För att kunna räkna med krafter behöver vi något hanterligt mått på dem.
Vi använder oss då av den regel i världens BIOS som säger att om ingenting
bromsar rörelsen kommer en kraft som verkar på en massa att öka dess hastighet.
Vi kallar den kraft som varje sekund ökar hastigheten hos en massa på 1 kg med
1 m/s för 1 N (Newton).Vi har alltså att
1 N = 1 kg m/s2
Vi använder oss av krafter för att åstadkomma önskade förändringar där och när
vi vill ha dem.Men förändringar inträffar också hela tiden spontant.Om vi vill
åka med ett luftskepp från Stockholm till Göteborg startar vi en drivmotor som
ger en kraft som förflyttar skeppet mot Göteborg.Denna kraft gånger den väg vi
färdas är det arbete,d v s den energi,som vi måste tillföra.Men det är viktigt
att observera att denna energitillförsel inte är nödvändig för att vi skall
komma till Göteborg i och för sig.Den är nödvändig för att vi skall kunna
förutsäga när vi kommer till Göteborg.Om vi lät skeppet driva omkring i luft-
havet i oändlig tid skulle vi naturligtvis,förr eller senare,hamna över
Göteborg och då skulle vi alltså ha fullbordat resan.Men det är ett mycket
opraktiskt sätt att resa.Vi behöver åtminstone någon typ av kraft som gör att
vi kan förutsäga färdvägen lite bättre.
Brus
====
Värme är slumpmässiga molekylrörelser (eller strålningsvärme). I en gas far
molekylerna omkring samtidigt som de roterar. I ett fast ämne vibrerar
molekylerna kring sina jämviktslägen.
Om man, med allt större noggrannhet försöker bestämma läget hos ytan av ett
stycke fast materia kommer man så småningom till problemet att det inte går
att komma längre därför att de atomer som utgör ytan hela tiden rör sig.
Om man observerar en liten partikel som svävar i en vätska finner man att
den rör sig med knyckiga slumpmässiga rörelser (Browns rörelse) som beror
på kollisioner med vätskemolekyler.
Kollisioner kan även medföra att elektroner slås ut från sina lägen i
elektronskalen vilket ger en slumpmässigt varierande spänning, d v s ett
elektroniskt brus.
När man i teleteknikens barndom försökte signalera över allt större avstånd
genom att förstärka den mottagna signalen med allt högre förstärkning fann
man att man inte bara förstärkte signalen utan också ett brus. Och när
signalen drunknade i bruset kunde man inte komma längre genom att öka
förstärkningen.
Slumpmässiga, d v s oförutsägbara, händelser inträffar. Det är bara en liten
del av alla händelser som är förutsägbara genom att de har en känd orsak.
Även när det finns en känd orsak kan det finnas oförutsägbarhet om detaljer i
verkan. Värme är en orsak till molekylrörelse men hastighet och riktning för
en enskild molekyl är oförutsägbar.
Temperatur är ett mått på variansen på molekylhastigheten. Om variansen är
skiljd från noll kan vi förutsäga att en viss molekyl kommer att röra sig men
det säger ingenting om åt vilket håll och det ger bara en antydan om hur
fort den kommer att röra sig.
För en ideal gas gäller
m s2 = 3 k T
där
m molekylens massa i kg
s2 variansen på den slumpmässiga molekylhastigheten
k Boltzmanns konstant
T absoluta temperaturen i K
Styrkan hos en signal avtar med avståndet (i tid och/eller rum) från orsaken.
Bruset beror på temperaturen hos bakgrunden och temperaturen hos mottagaren.
Med ökande avstånd kommer således signalen så småningom att drunkna i bruset.
Våra förutsägelser blir alltså alltmer osäkra.
Vi kan t ex göra väderprognoser baserade på dagens kända orsaker till väder-
förändringar men bruset genererar hela tiden oförutsägbara orsaker till
förändringar och allteftersom tiden går kommer dessa allt mer att dominera
över dagens kända orsaker.
Allt vi gör är alltså förgängligt. Vilken verkan vi än åstadkommer kommer den
så småningom att drunkna i de slumpmässiga förändringar som bruset orsakar.
Den fyrdimensionella världen
============================
Med avståndet mellan punkterna A och B menar vi det minsta antal enhetsceller
man måste passera för att komma från A till B.På liknande sätt kan man
definiera tidsavståndet mellan händelserna a och b som det antal enhetshändelser
som inträffar mellan a och b.
Ett sätt att hantera avstånd mellan ett stort antal punkter är att lägga in dem
i ett treaxligt koordinatsystem.I stället för att ange alla möjliga avstånd kan
vi då ange alla punkters koordinater och ur dessa beräkna de avstånd vi vill
veta.
Det ligger nära till hands att lägga till en koordinataxel och använda den för
att ange tidskoordinat.Med avstånd i ett sådant fyraxligt koordinatsystem menar
vi då,inte bara antal enhetsceller mellan A och B utan också antal enhetshändelser
mellan att vi utgår från A och kommer fram till B.
Om vi använder ett sådant fyraxligt koordinatsystem kan vi ge tid två olika
betydelser.Vi kan dels tala om tid som en förändringsparameter.Vi kan kalla
detta för parametertid.Och vi kan tala om tid som en lägeskoordinat i vår
fyrdimensionella värld.
Så kan vi naturligtvis göra men normalt växer parametertiden och koordinattiden
likadant.Finns det då någon anledning att skilja på begreppen?Finns det något
i världens BIOS som går att beskriva genom att vi skiljer på begreppen?
Världens BIOS uppför sig faktiskt som om det fanns något som strömmade med viss
hastighet åt något håll i den fyrdimensionella rymden.Vi har inget bra namn på
detta något.Det har kallats världseter eller Brahma men låt oss för enkelhets
skull kalla det för eter.
Om allt står stilla i rummet strömmar etern i tidsriktning.Och hastigheten blir
c = t/τ
där
c = eterns strömningshastighet d v s ljushastigheten
t = koordinattid
τ = parametertid
Allt står då stilla i rummet och följer med en eter som strömmar i tidsled.
Om något rör sig i rummet kan vi uppfatta detta som att hastigheten där ändrar
riktning.Om något föremål flyttar sig sträckan s på parametertiden τ säger vi
att det rör sig med hastigheten v enligt
v = s/τ = c sin(α)
där
α = vridningsvinkeln för föremålets hastighetsvektor
Man kan uppfatta ljus som en ström av partiklar,fotoner,som rör sig med ljus-
hastighet i rummet.Fotonernas hastighetsvektor har alltså vridits 90 grader så
att de rör sig i rummet men står stilla i tiden.
Om man,likt Munchhausen,kunde hoppa ombord på en foton och titta bakåt skulle
man se startplatsen sådan den såg ut när man startade.Alla klockor på startplatsen
skulle då stå stilla.Man skulle inte röra sig i startplatsens tidsled.Men man
skulle röra sig med ljushastighet i någon annan riktning som man själv skulle
uppfatta som tidsriktningen och de som var kvar på startplatsen skulle kalla en
rumsriktning.
Gravitation
===========
Betrakta två partiklar A och B på avståndet ab.
I fig 1 anger den blå ytan alla punkter som ligger närmare A än vad B gör.Och
den gula ytan anger punkter som ligger längre ifrån A än vad B gör.Om nu B
rör sig helt slumpmässigt i förhållande till A finns det uppenbarligen många
fler punkter dit B kan gå för att öka avståndet till A än punkter dit B kan
gå för att minska avståndet.
 Fig 4
Sannolikheten att avståndet ökar är alltså större än sannolikheten att det
minskar.Partiklarna kommer alltså att uppföra sig som om de stötte bort varandra.
Vi kan uppfatta detta som en utåtriktad gravitation.
Vi har alla sett att ljuset bryts vid en vattenyta eller vid en glasyta i t ex
en lins.Detta kan förklaras med att ljushastigheten är lägre i vatten och glas
än den är i luft.Det förefaller alltså som om ljushastigheten c är lägre i
områden med större antal ettor.Om vi använder bilden av en eter som strömmar i
tidsled i en fyrdimensionell rymd skulle detta innebära att etern släpar efter
i områden med förhållandevis många ettor.En stor massa innebär alltså en
etereftersläpning som medför att runt massan kröks eterns strömningsriktning
inåt mot massan.Eterns strömningsriktning får alltså här en komposant i
rumsriktning.En partikel som svävar fritt i etern kommer alltså att dras in
mot massan.
Michelson-Morleys spegelförsök visade att jorden inte rör sig i förhållande
till en omgivande eter.
Eftersom föremål kan röra sig i förhållande till varandra ansåg man att de
inte alla kunde vara i vila i förhållande till omgivande eter.Man tolkade
därför försöket som att det inte kan finnas någon eter.
I ett medium som i det närmaste är inkompressibelt,som vatten,gäller att mediets
strömningsriktning blir praktiskt taget densamma i närliggande punkter.Men redan
med den kompressibilitet som luft har kan man ha närliggande vindbyar med
olika riktning.
Ombord på en ballong blåser det aldrig trots att man kan ha betydande hastighet
i förhållande till andra ballonger inom synhåll.Luftens kompressibilitet gör att
ballonger som alla befinner sig i vila i förhållande till omgivande luft ändå
kan röra sig i förhållande till varandra.
Och varför skulle etern vara inkompressibel?
Är inte föreställningen att jorden faktiskt befinner sig i vila i förhållande till
omgivande eter på samma sätt som en ballong är i vila i förhållande till omgivande
luft en mer näraliggande tolkning av Michelson-Morleys spegelförsök?
Runt massor får vi alltså en "etervind" in mot dem.Om man befinner sig tillräckligt
nära en tillräckligt stor massa kommer denna etervind att dominera över den
utåtriktade gravitationen och vi får en inåtriktad gravitation.
Gravitation är alltså utåtriktad men lokalt kring en massa inåtriktad.
Liv
===
Till en dator skaffar vi ett antal program som,med hjälp av datorns operativsystem,
åstadkommer spektakulära effekter.Till världsdatorn har bl a uppstått ett program
som vi kallar "Liv".
Liksom vi till datorn använder disketter och CD-rom för att lagra program använder
liv DNA för lagring av programet.
Vi har nyligen upptäckt hur denna lagring går till och vi är nu i full gång med
att skapa en debugger som fått namnet HUGO.
Med HUGO öppnar vi programet liv för läsning i assemblerspråk.Vi får allt i form
av anrop till världens BIOS men fortfarande har vi långt kvar innan vi kan tolka
vad vi får fram.Alla som försökt dekompilera ett program vet hur svårt det är att
hålla reda på vad instruktionerna innebär.Eftersom en dator blandar instruktioner
och data i samma minne brukar man snart blanda ihop data med instruktioner
och gå vilse i programet.Och när det gäller världens BIOS vet vi inte ens hur
data och instruktioner hålls isär.Och redan nu visar HUGO en mängd programtext
som vi inte vet om den har någon funktion.Är det bara rester av gammal fel-
programering?Är det element som haft en funktion men som senare ersatts av andra
element?Eller är det livsviktiga instruktioner?
Olika energiformer
==================
Enhetshändelser inträffar ständigt men med våra trubbiga sinnen och instrument kan
vi inte utnyttja enstaka enhetshändelser.Vi är hänvisade till att arbeta med
händelsekedjor som ger så stora förändringar att vi kan uppfatta dem.I stället
för att arbeta med enstaka enhetsceller och enhetshändelser arbetar vi med
medelvärde,varians och rumshastighet.
Våra sinnen är programerade för att anropa världens BIOS via några olika typer
av anrop och vi tolkar detta som att vi har tillgång till olika energiformer.
Men även om vi upplever att det är skillnad mellan t ex elektrisk energi och
värme behandlar vi alla energiformer enligt samma regler.
Oavsett vilken energiform det är fråga om betraktar vi energi som en produkt
av en mängd (extensiv faktor) och en intensitet (intensiv faktor).
Mängden kan bero på hur vi avgränsar det system vi betraktar.Om vi har en hink
med varmt vatten så har vi värme i den.Om vi häller upp halva hinken i en skål
får vi halva värmeenergin i skålen men det betyder inte att värme omvandlats
till någon annan energiform bara att vi avgränsat mängden på ett nytt sätt.
Om däremot den intensiva faktorn ändras kan,men behöver inte,energi omvandlas
till annan energiform.Om vi låter vattnet i hinken driva en värmemaskin omvandlas
en del värme till arbete och intensiteten,d v s temperaturen hos vattnet,sjunker.
Om den intensiva faktorn ändras från T1 till T2 kan alltså energi
omvandlas till annan energiform t ex till utvinnbart arbete.Det arbete som går att
få ut från en sådan omvandling för mängden S är
W = S (T1 - T2)
Läran om energiomvandling har utvecklats vid olika tidpunkt för olika energiformer.
Resultatet har blivit att man valt begrepp,sorter och mätmetoder på något olika
sätt så att det inte alltid är uppenbart att det grundläggandet resonemanget är
identiskt.Det krävs alltså lite tankearbete för att se vad som motsvarar vad men
det lönar sig att inse att t ex elektrisk intensitet är arbete per laddningsenhet
(V = J/As),potentiell intensitet är arbete per tyngdenhet (höjd i m är J/tyngd i N),
värmeintensitet (=temperatur) är arbete per entropienhet (K = J/(J/K)),intensitet för
pneumatisk energi (=volym) är arbete per tryckenhet (m3 = J/Pa),intensitet för
rörelseenergi (=hastighet) är arbete per rörelsemängd (=impuls) o s v.
Genom att på detta sätt se hur man organiserat tänkandet slipper man läsa statik,
dynamik,ellära,värmelära,pneumatik,fysikalisk kemi mm som av varandra oberoende
läror.Man kan identifiera det som är gemensamt och bara slå i sig det lilla som
blir kvar som unikt för varje energiform t ex vad begreppen har för namn.
Mängdändring
============
Man kan,som sagt,inte omvandla energi bara genom att ändra gränserna för den
energimängd man betraktar.Men det förekommer att mängd faktiskt skapas eller
förintas vilket medför energiomvandling.
Uppdelningen i extensiv mängdfaktor som inte ger energiomvandling vid förändring
och intensiv faktor som är lika för alla delar av mängden och som ger energi-
omvandling vid förändring är alltså inte så självklar som det kan förefalla vid
första påseendet.
För pneumatisk energi är tryck extensiv och volym intensiv faktor.Man kan se det
som att trycket åstadkoms genom att man tillför luftmängd och varje delmängd som
man tillför fyller ut hela volymen så att alla delmängderna har samma volym d v s
samma intensitet.Men det känns ändå lite besynnerligt att inte betrakta volym som
en mängdstorhet.Och om man minskar volymen på en sluten behållare så ökar trycket,
extensiv och intensiv faktor är då kopplade till varandra så att båda ändras.
Hur hanterar man fall där mängden inte är konstant?
Betrakta en vattenfylld bassäng med vertikala väggar.Den energi som vi kan ta ut
om vi tömmer bassängen är vattnets tyngd gånger dess fallhöjd.
Om vattenytan är A och bassängens höjd h blir vattnets tyngd
Fig 4
Sannolikheten att avståndet ökar är alltså större än sannolikheten att det
minskar.Partiklarna kommer alltså att uppföra sig som om de stötte bort varandra.
Vi kan uppfatta detta som en utåtriktad gravitation.
Vi har alla sett att ljuset bryts vid en vattenyta eller vid en glasyta i t ex
en lins.Detta kan förklaras med att ljushastigheten är lägre i vatten och glas
än den är i luft.Det förefaller alltså som om ljushastigheten c är lägre i
områden med större antal ettor.Om vi använder bilden av en eter som strömmar i
tidsled i en fyrdimensionell rymd skulle detta innebära att etern släpar efter
i områden med förhållandevis många ettor.En stor massa innebär alltså en
etereftersläpning som medför att runt massan kröks eterns strömningsriktning
inåt mot massan.Eterns strömningsriktning får alltså här en komposant i
rumsriktning.En partikel som svävar fritt i etern kommer alltså att dras in
mot massan.
Michelson-Morleys spegelförsök visade att jorden inte rör sig i förhållande
till en omgivande eter.
Eftersom föremål kan röra sig i förhållande till varandra ansåg man att de
inte alla kunde vara i vila i förhållande till omgivande eter.Man tolkade
därför försöket som att det inte kan finnas någon eter.
I ett medium som i det närmaste är inkompressibelt,som vatten,gäller att mediets
strömningsriktning blir praktiskt taget densamma i närliggande punkter.Men redan
med den kompressibilitet som luft har kan man ha närliggande vindbyar med
olika riktning.
Ombord på en ballong blåser det aldrig trots att man kan ha betydande hastighet
i förhållande till andra ballonger inom synhåll.Luftens kompressibilitet gör att
ballonger som alla befinner sig i vila i förhållande till omgivande luft ändå
kan röra sig i förhållande till varandra.
Och varför skulle etern vara inkompressibel?
Är inte föreställningen att jorden faktiskt befinner sig i vila i förhållande till
omgivande eter på samma sätt som en ballong är i vila i förhållande till omgivande
luft en mer näraliggande tolkning av Michelson-Morleys spegelförsök?
Runt massor får vi alltså en "etervind" in mot dem.Om man befinner sig tillräckligt
nära en tillräckligt stor massa kommer denna etervind att dominera över den
utåtriktade gravitationen och vi får en inåtriktad gravitation.
Gravitation är alltså utåtriktad men lokalt kring en massa inåtriktad.
Liv
===
Till en dator skaffar vi ett antal program som,med hjälp av datorns operativsystem,
åstadkommer spektakulära effekter.Till världsdatorn har bl a uppstått ett program
som vi kallar "Liv".
Liksom vi till datorn använder disketter och CD-rom för att lagra program använder
liv DNA för lagring av programet.
Vi har nyligen upptäckt hur denna lagring går till och vi är nu i full gång med
att skapa en debugger som fått namnet HUGO.
Med HUGO öppnar vi programet liv för läsning i assemblerspråk.Vi får allt i form
av anrop till världens BIOS men fortfarande har vi långt kvar innan vi kan tolka
vad vi får fram.Alla som försökt dekompilera ett program vet hur svårt det är att
hålla reda på vad instruktionerna innebär.Eftersom en dator blandar instruktioner
och data i samma minne brukar man snart blanda ihop data med instruktioner
och gå vilse i programet.Och när det gäller världens BIOS vet vi inte ens hur
data och instruktioner hålls isär.Och redan nu visar HUGO en mängd programtext
som vi inte vet om den har någon funktion.Är det bara rester av gammal fel-
programering?Är det element som haft en funktion men som senare ersatts av andra
element?Eller är det livsviktiga instruktioner?
Olika energiformer
==================
Enhetshändelser inträffar ständigt men med våra trubbiga sinnen och instrument kan
vi inte utnyttja enstaka enhetshändelser.Vi är hänvisade till att arbeta med
händelsekedjor som ger så stora förändringar att vi kan uppfatta dem.I stället
för att arbeta med enstaka enhetsceller och enhetshändelser arbetar vi med
medelvärde,varians och rumshastighet.
Våra sinnen är programerade för att anropa världens BIOS via några olika typer
av anrop och vi tolkar detta som att vi har tillgång till olika energiformer.
Men även om vi upplever att det är skillnad mellan t ex elektrisk energi och
värme behandlar vi alla energiformer enligt samma regler.
Oavsett vilken energiform det är fråga om betraktar vi energi som en produkt
av en mängd (extensiv faktor) och en intensitet (intensiv faktor).
Mängden kan bero på hur vi avgränsar det system vi betraktar.Om vi har en hink
med varmt vatten så har vi värme i den.Om vi häller upp halva hinken i en skål
får vi halva värmeenergin i skålen men det betyder inte att värme omvandlats
till någon annan energiform bara att vi avgränsat mängden på ett nytt sätt.
Om däremot den intensiva faktorn ändras kan,men behöver inte,energi omvandlas
till annan energiform.Om vi låter vattnet i hinken driva en värmemaskin omvandlas
en del värme till arbete och intensiteten,d v s temperaturen hos vattnet,sjunker.
Om den intensiva faktorn ändras från T1 till T2 kan alltså energi
omvandlas till annan energiform t ex till utvinnbart arbete.Det arbete som går att
få ut från en sådan omvandling för mängden S är
W = S (T1 - T2)
Läran om energiomvandling har utvecklats vid olika tidpunkt för olika energiformer.
Resultatet har blivit att man valt begrepp,sorter och mätmetoder på något olika
sätt så att det inte alltid är uppenbart att det grundläggandet resonemanget är
identiskt.Det krävs alltså lite tankearbete för att se vad som motsvarar vad men
det lönar sig att inse att t ex elektrisk intensitet är arbete per laddningsenhet
(V = J/As),potentiell intensitet är arbete per tyngdenhet (höjd i m är J/tyngd i N),
värmeintensitet (=temperatur) är arbete per entropienhet (K = J/(J/K)),intensitet för
pneumatisk energi (=volym) är arbete per tryckenhet (m3 = J/Pa),intensitet för
rörelseenergi (=hastighet) är arbete per rörelsemängd (=impuls) o s v.
Genom att på detta sätt se hur man organiserat tänkandet slipper man läsa statik,
dynamik,ellära,värmelära,pneumatik,fysikalisk kemi mm som av varandra oberoende
läror.Man kan identifiera det som är gemensamt och bara slå i sig det lilla som
blir kvar som unikt för varje energiform t ex vad begreppen har för namn.
Mängdändring
============
Man kan,som sagt,inte omvandla energi bara genom att ändra gränserna för den
energimängd man betraktar.Men det förekommer att mängd faktiskt skapas eller
förintas vilket medför energiomvandling.
Uppdelningen i extensiv mängdfaktor som inte ger energiomvandling vid förändring
och intensiv faktor som är lika för alla delar av mängden och som ger energi-
omvandling vid förändring är alltså inte så självklar som det kan förefalla vid
första påseendet.
För pneumatisk energi är tryck extensiv och volym intensiv faktor.Man kan se det
som att trycket åstadkoms genom att man tillför luftmängd och varje delmängd som
man tillför fyller ut hela volymen så att alla delmängderna har samma volym d v s
samma intensitet.Men det känns ändå lite besynnerligt att inte betrakta volym som
en mängdstorhet.Och om man minskar volymen på en sluten behållare så ökar trycket,
extensiv och intensiv faktor är då kopplade till varandra så att båda ändras.
Hur hanterar man fall där mängden inte är konstant?
Betrakta en vattenfylld bassäng med vertikala väggar.Den energi som vi kan ta ut
om vi tömmer bassängen är vattnets tyngd gånger dess fallhöjd.
Om vattenytan är A och bassängens höjd h blir vattnets tyngd
 På liknande sätt gäller för rörelseenergi att rörelsemängden d v s impulsen mv
varierar med intesiteten d v s med hastigheten v.Och även här får vi ett liknande
uttryck för uttagbar energi.Den blir
W = m v2/2
Transformatorn och väduren
========================
Om man har energimängden E = S1 T1 kan man omvandla denna till den
lika stora energimängden E = S2 T2 . Man kan alltså ändra intensitet och
mängd så länge deras produkt förblir oförändrad. En stor tyngd med liten
höjd kan alltså omvandlas till en liten tyngd med stor höjd. En stor laddning
med liten spänning kan ge en liten laddning med hög spänning. Men hur gör
man för att åstadkomma en sådan omvandling?
Ett vanligt sätt är att omvandla till annan energiform och därefter återgå till
den ursprungliga energiformen. Om man har lägesenergi kan man omvandla
den till rörelseenergi som man omvandlar till lägesenergi.
Om en kula med tyngden m1g ligger på ett bord med höjden h1 har man
lägesenergin E = m1g h1. Om kulan rullar över bordskanten omvandlas
denna lägesenergi till rörelseenergi. På golvet kan man så lägga en
gungbräda med en kula med tyngden m2g på den sida som inte träffas av
den fallande kulan. Arrangerar man det hela på rätt sätt kan resultatet
bli att hela rörelseenergin (som är lika med den ursprungliga lägesenergin)
överförs till den andra kulan som kastas upp till höjden h2 så att
E = m1g h1 = m2g h2
Anordningen är alltså en transformator som transformerar kulhöjden h1 till
kulhöjden h2.
Inom elöverföring använder man ofta transformatorer för att omvandla
spänning mellan de krav som ställs för överföringen och de krav som ställs
för användningen. Den energi som tillförs transformatorns primärlindning
omvandlas till magnetisk energi i transformatorkärnan och den magnetiska
energin omvandlas till elektrisk energi i primär och sekundärlindningen. Det
man inte tar ut via sekundärlindningen återmatas via primärlindningen
tillbaka till energikällan.
Antag att jag bor vid en strand. Huset ligger på höjden h2 över sjöytan.
På vägen upp till huset finns en källa som ligger på höjden h1 över
sjöytan så att h1 är mindre än h2. Hur skall jag göra för att
få vatten från källan upp till huset?
Jag kan använda en hydraulisk vädur eller med ett annat ord en stöthävert.
Från källan drar jag ett rör ner i sjön. I neränden på detta sätter jag en
förgrening där ett rör går upp till huset. I röret upp till huset sätter jag en
backventil och nedanför grenen sätter jag en styrd ventil. Jag fyller systemet
med vatten och öppnar den styrda ventilen. Vatten strömmar då från källan
till sjön. När vattnet fått ordentlig fart stänger jag den styrda ventilen.
För att bromsa ett yxhugg på bromssträckan noll krävs oändlig kraft. På
samma sätt krävs oändligt mottryck för att på bromssträckan noll stoppa ett
vatttenflöde i ett slutet rör. När jag stänger den styrda ventilen får jag
alltså ett stagnationstryck som blir oändligt om det inte finns någon möjlighet
för vattnet att bromsa in genom att något sviktar eller genom att det finns
någon annan väg för vattnet att strömma. Här finns en annan väg. Det är
röret upp till huset. När jag stänger den styrda ventilen stiger alltså trycket
tills det överstiger trycket i röret upp till huset. Då öppnar backventilen och
vatten strömmar upp till huset.
Källvattnets lägesenergi omvandlas till rörelseenergi när vatten strömmar
från källan till sjön. När jag stänger den styrda ventilen omvandlas rörelse-
energin till lägesenergi när vatten trycks upp till huset.
Den elektriska motsvarigheten till en vattenmassa som strömmar i ett rör är
en elektrisk ström genom en induktans. Om man plötsligt bryter strömmen
får man en spänning som motsvarar ett stagnationstryck. Spänningen blir
U = L di/dτ
På samma sätt som man kan använda en hydraulisk vädur för att pumpa
vatten från en låg till en hög nivå kan man göra en "elektrisk vädur" som
pumpar elektrisk laddning från en låg spänning till en hög spänning.
På liknande sätt gäller för rörelseenergi att rörelsemängden d v s impulsen mv
varierar med intesiteten d v s med hastigheten v.Och även här får vi ett liknande
uttryck för uttagbar energi.Den blir
W = m v2/2
Transformatorn och väduren
========================
Om man har energimängden E = S1 T1 kan man omvandla denna till den
lika stora energimängden E = S2 T2 . Man kan alltså ändra intensitet och
mängd så länge deras produkt förblir oförändrad. En stor tyngd med liten
höjd kan alltså omvandlas till en liten tyngd med stor höjd. En stor laddning
med liten spänning kan ge en liten laddning med hög spänning. Men hur gör
man för att åstadkomma en sådan omvandling?
Ett vanligt sätt är att omvandla till annan energiform och därefter återgå till
den ursprungliga energiformen. Om man har lägesenergi kan man omvandla
den till rörelseenergi som man omvandlar till lägesenergi.
Om en kula med tyngden m1g ligger på ett bord med höjden h1 har man
lägesenergin E = m1g h1. Om kulan rullar över bordskanten omvandlas
denna lägesenergi till rörelseenergi. På golvet kan man så lägga en
gungbräda med en kula med tyngden m2g på den sida som inte träffas av
den fallande kulan. Arrangerar man det hela på rätt sätt kan resultatet
bli att hela rörelseenergin (som är lika med den ursprungliga lägesenergin)
överförs till den andra kulan som kastas upp till höjden h2 så att
E = m1g h1 = m2g h2
Anordningen är alltså en transformator som transformerar kulhöjden h1 till
kulhöjden h2.
Inom elöverföring använder man ofta transformatorer för att omvandla
spänning mellan de krav som ställs för överföringen och de krav som ställs
för användningen. Den energi som tillförs transformatorns primärlindning
omvandlas till magnetisk energi i transformatorkärnan och den magnetiska
energin omvandlas till elektrisk energi i primär och sekundärlindningen. Det
man inte tar ut via sekundärlindningen återmatas via primärlindningen
tillbaka till energikällan.
Antag att jag bor vid en strand. Huset ligger på höjden h2 över sjöytan.
På vägen upp till huset finns en källa som ligger på höjden h1 över
sjöytan så att h1 är mindre än h2. Hur skall jag göra för att
få vatten från källan upp till huset?
Jag kan använda en hydraulisk vädur eller med ett annat ord en stöthävert.
Från källan drar jag ett rör ner i sjön. I neränden på detta sätter jag en
förgrening där ett rör går upp till huset. I röret upp till huset sätter jag en
backventil och nedanför grenen sätter jag en styrd ventil. Jag fyller systemet
med vatten och öppnar den styrda ventilen. Vatten strömmar då från källan
till sjön. När vattnet fått ordentlig fart stänger jag den styrda ventilen.
För att bromsa ett yxhugg på bromssträckan noll krävs oändlig kraft. På
samma sätt krävs oändligt mottryck för att på bromssträckan noll stoppa ett
vatttenflöde i ett slutet rör. När jag stänger den styrda ventilen får jag
alltså ett stagnationstryck som blir oändligt om det inte finns någon möjlighet
för vattnet att bromsa in genom att något sviktar eller genom att det finns
någon annan väg för vattnet att strömma. Här finns en annan väg. Det är
röret upp till huset. När jag stänger den styrda ventilen stiger alltså trycket
tills det överstiger trycket i röret upp till huset. Då öppnar backventilen och
vatten strömmar upp till huset.
Källvattnets lägesenergi omvandlas till rörelseenergi när vatten strömmar
från källan till sjön. När jag stänger den styrda ventilen omvandlas rörelse-
energin till lägesenergi när vatten trycks upp till huset.
Den elektriska motsvarigheten till en vattenmassa som strömmar i ett rör är
en elektrisk ström genom en induktans. Om man plötsligt bryter strömmen
får man en spänning som motsvarar ett stagnationstryck. Spänningen blir
U = L di/dτ
På samma sätt som man kan använda en hydraulisk vädur för att pumpa
vatten från en låg till en hög nivå kan man göra en "elektrisk vädur" som
pumpar elektrisk laddning från en låg spänning till en hög spänning.
 Fig 5
Den viktiga skillnaden mellan en transformator och en elektrisk vädur är att
transformatorn transformrar en växelspänning U1 till en annan spänning U2
där förhållandet mellan dessa båda spänningar bestäms av förhållandet
mellan antalet lindningsvarv i primärlindning och antalet lindningsvarv i
sekundärlindning. Stöthäverten, d v s väduren, däremot överför laddning från
matningsspänningen U1 till utspänningen U2 oberoende av vilket värde U2 har.
Fig 5
Den viktiga skillnaden mellan en transformator och en elektrisk vädur är att
transformatorn transformrar en växelspänning U1 till en annan spänning U2
där förhållandet mellan dessa båda spänningar bestäms av förhållandet
mellan antalet lindningsvarv i primärlindning och antalet lindningsvarv i
sekundärlindning. Stöthäverten, d v s väduren, däremot överför laddning från
matningsspänningen U1 till utspänningen U2 oberoende av vilket värde U2 har.
 Fig 1
Om jag i stället använder laplacetransformerna överför jag integrationen till en
multiplikation med 1/s.Jag kan nu se det som att e multipliceras med G och ger
c enligt
e(s) G(s) = c(s)
Om jag öppnar kranarna till det konstanta flödet I (liter/sek) blir
e(s) = I 1/s = I/s
eftersom laplacetransformen för 1 är 1/s.
Överföringen är en integration vilket innebär att
G(s) = 1/s
vilket ger
I 1 1
c(s) = e(s) G(s) = --- --- = I ----
s s s2
Den tidsfunktion som motsvarar laplacetransformen 1/s2 är t.Vi får
alltså
c(t) = I t
Om man multiplicerar kranflödet i liter/sek med det antal sekunder man tappar får
man alltså vattenmängden.Det inser man naturligtvis direkt men det blir inte fel om
man försöker komma fram till resultatet med hjälp av laplacetransformen.Och när
e(t) och G blir mer komplicerade blir inte slutresultatet lika självklart.
Vektoranalys
============
Om man är intresserad av vindar finns det anledning att beskriva atmosfären
på sådant sätt att man kan dra slutsatser om vilka vindar som blåser, vilka
som kommer att blåsa och vilka som har blåst.
Vind är volymflöde som orsakas av tryckskillnad. Det kan alltså vara lämpligt
att beskriva atmosfären genom att ange trycket i ett antal olika punkter.
Tryck är en endimensionell vektor, d v s en skalar. Det räcker med att ange en
enda siffra för att ange trycket i en viss punkt. Denna siffra är tryck-
skillnaden mellan punkten och en absolut nollpunkt för tryck. Tryck är alltså
en potential, d v s en skalär storhet som anges som avvikelse från en nollpunkt.
Om vi beskriver atmosfären på detta sätt säger vi att den är ett potentialfält.
Om vi vet trycket p i varje punkt kan vi rita tryckkartor där vi sammanbinder
punkter med samma tryck till isobarer. På tvådimensionella kartor blir
isobarerna linjer och i tredimensionella kartor blir isobarerna ytor.
Men det är inte tryck utan tryckskillnad som driver vind. Att vi vet trycket i
en viss punkt räcker inte för att kunna säga om vinden ökar eller minskar i
punkten. Vi behöver veta hur trycket förändras i punktens omgivning.
För att beskriva tryckförändringar i punktens omgivning lägger vi in ett
treaxligt koordinatsystem med vinkelräta axlar (x , y , z) och origo i punkten.
Så går vi ett steg i x-riktningen och mäter upp tryckändringen dpx. Vi
dividerar med steglängden dx och får ett mått dpx/dx på hur snabbt trycket
ändras i x-riktningen. Så gör vi likadant i y-riktningen och i z-riktningen och
får tre siffror som anger hur snabbt trycket ändras i området runt punkten.
Vi kan alltså beskriva tryckändringen runt punkten med tre siffror d v s med en
tredimensionell vektor. Denna vektor kallas för gradient och anges med operatorn
grad. Vi kan alltså skriva
grad p = (dpx/dx dpy/dy dpz/dz)
Gradienten för en potential d v s för en skalar är alltså en vektor som anger hur
snabbt potentialen ändras i olika riktningar.
Vind är volymflöde genom ytenhet. För att mäta vinden kan vi göra en öppning med
ytan 1 m2 och se hur många m3 som passerar genom öppningen per sekund.
Sorten för vind blir då (m3/s)/m2 = m/s alltså en hastighet som vi kallar
vindhastighet. Vi betecknar vind d v s vindhastighet med v.
Vind har inte bara ett värde den har också en riktning. Den kan alltså inte som
ses som en skalär potential utan den måste behandlas som en vektor. Vi kan t ex
ange den genom att ange vind i x-riktningen (vx), vind i y-riktningen (vy) och
vind i z-riktningen (vz). Till varje punkt i atmosfären hör alltså en skalar
som anger trycket i punkten, en vektor som anger tryckändringen i punkten
och en vektor som anger vinden i punkten.
Vind i vindriktningen kallas för vindens belopp och betecknas |v|.
Vi omsluter en punkt med en sluten yta S t ex med en klotyta. Så delar vi upp
denna yta i smådelar dS som är så små att vinden kan anses vara lika i alla
delar av en sådan småyta. |v| dS cos α är då det volymflöde som strömmar ut
genom dS (α är vinkeln mellan v och normalen till dS). På en tidsenhet bortförs
alltså via dS luftvolymen |v| dS cos α från den volym som omsluts av S. Summerar
vi över alla dS får vi den luftvolym som varje tidsenhet bortförs från volymen
inom S. För att få ett mått som inte beror på hur stor volym V som S omsluter
dividerar vi med V. Vi har nu fått ett mått på hur mycket volym (observera
skillnaden mellan omsluten volym V och den flödande luftvolym v som kan
skapas) som skapas inom S och blåser ut utan att ha blåst in. Vi har alltså
fått ett mått på punkten som vindkälla. Detta anges med operatorn div som
alltså anger källstyrka.
I många fall gäller att den vind som blåser in i en punkt är lika stor som
den vind som blåser ut från punkten. Källstyrkan är då 0 och vi säger att
vinden källfri. Men om t ex solen värmer i punkten så att luftens volym ökar
kommer större volym att lämna punkten än den volym som kom in i punkten
(eftersom luft är kompressibel kommer även tryckändring att ge volymändring).
Vi får då div v > 0.
Ett flöde (t ex vind) av något (t ex luftvolym) kan alltså beskrivas som ett
vektorfält där varje punkt tilldelas en vektor (v) som anger flödets storlek i
olika riktningar. Divergensen för denna vektor (div v) anger källstyrkan för
det som flödar.
Div v, d v s källstyrkan, är en skalär storhet.
Inom ellära använder man Kirchhoffs första lag som säger att summan av alla
strömmar till en punkt är lika med summan av alla strömmar från punkten.
Kirchhoffs första lag säger alltså att strömmen är ett källfritt flöde. Vi
har alltså div I = 0 i alla punkter. Antalet laddningsbärare, d v s antalet
elektroner, som strömmar i ledningarna och utgör det flöde som är den
elektriska strömmen ändras alltså inte i någon punkt.
Maxwells ekvationer är en annan formulering av Kirchhoffs lagar och där har
Kirchhoffs första lag formen
div I = 0
Detta gäller om inte laddningsfördelningen ändras.
Vi kan ha både vind och elektrisk ström som varierar trots att källstyrkan är
noll. Men vi kan inte ha ett nettoflöde in i eller ut ur en punkt om käll-
styrkan är noll. För källor och sänkor i ett flöde är divergensen skiljd från
noll.
Små flöden kan flyta samman till ett stort och ett stort flöde kan grena sig i
många små även om källstyrkan är noll. Att källstyrkan i en punkt är större
än noll innebär att ett flöde uppstår i punkten utan att komma in i punkten
och att källstyrkan är mindre än noll innebär att ett flöde försvinner i
punkten.
Div v ≠ 0 betyder att en del av flödet v kommer från ingenstans eller
försvinner i intet. Vi kan naturligtvis säga att ett flöde kommer från eller
försvinner till en annan dimension. Om vi t ex studerar horisontella vindar
kan vi göra det i ett tvådimensionellt system med x-axeln i öst-väst och
y-axeln i nord-syd. Om vi då har div v ≠ 0 kan vi naturligtvis skriva
div v = dvz/dz och tolka det som att en del av v kommer från eller försvinner
till en tredje dimension (z). Om vi så lägger in en vertikal axel och kallar
den för z-axeln, d v s inför den tredje dimensionen som en vertikal
dimension tolkar vi vz som fallvind eller uppvind som tillför
eller bortför horisontell vind. Om detta var hela orsaken till att div v i det
tvådimensionella systemet var skiljd från noll blir div v = 0 i det
tredimensionella systemet. Skulle det dessutom finnas andra skäl,
t ex att uppvärmning ger volymutvidgning kommer div v inte att minska
ända till noll utan ha ett restvärde som vi kan tolka som kommande från
ytterligare en dimension.
Antag att vi är intresserade av en viss punkt A. Vi lägger in en plan yta
som innehåller A. Så går vi runt en sluten väg runt A i ytan. För varje steg
vi tar multiplicerar vi steglängden med vindhastigheten i stegriktningen.
Alla dessa produkter adderar vi tills vi är tillbaka till utgångspunkten. Vi
bildar alltså
S
∫ v dl
L
där
dl är steglängden och L betecknar en sluten väg
Värdet av denna integral beror på hur vi valt att lägga planet. Vi väljer så
det plan som ger maximalt värde på denna integral. Så dividerar vi med
den ytan som gångvägen omsluter och kallar det vi då får fram för beloppet
av rot v.
Om vi får lika mycket medvind som motvind när vi går runt en sluten väg är
rot v = 0. Vi säger då att vinden är virvelfri. Skulle det däremot blåsa en
virvelvind runt A kan vi följa med virveln och gå runt A så att vi hela vägen
får medvind. Vi beskriver detta med en vektor som kallas rot v som har
beloppet lika med ovanstående integral dividerad med den omslutna ytan
och riktningen sammanfallande med normalen till den omslutna ytan.
Ett exempel på ett praktiskt taget virvelfritt fält är gravitationen vid
markytan. Antag att vi går runt en sluten väg och för varje steg
multiplicerar tyngden med höjdändringen. När vi kommer tillbaka till
utgångspunkten och lägger ihop alla dessa produkter får vi det arbete
som uträttats under vägen och detta blir alltid noll hur vi än går. Det i
sin tur innebär att arbetet som uträttas när vi går från punkt A till punkt B
blir lika stort vilken väg vi än går. Vi kan då tilldela punkt A en potential
gA som motsvarar arbetet att föra en massenhet från en
referenspunkt till A. Och på motsvarande sätt kan vi tilldela punkt B en
potential gB. Arbetet att föra massan m från A till B blir
då W enligt
W = m gA - m gB = m (gA - gB)
Inom ellära använder man Kirchhoffs andra lag som säger att summan
av alla spänningar längs en sluten väg är noll, d v s att fältstyrkan är
virvelfri.
I Maxwells ekvationer har Kirchhoffs andra lag formuleringen
rot E = 0
(OBS att E här betyder elektrisk fältstyrka, inte energi)
Detta gäller om det inte finns några varierande magnetiska fält. Tids-
derivatan hos ett magnetiskt fält ger elektriska virvlar.
I ett tredimensionellt system är vi vana vid att se virvlar. Vi har alla sett
virvelvindar och virvlar när vattnet runner ur badkaret. I tre dimensioner
kan vi göra en uppdelning i ett plan och en axel vinkelrät mot planet. En
virvel runt denna axel kommer då att ligga i planet. För ett fyrdimensionellt
system tillkommer emellertid möjligheter som inte är helt lätta att före-
ställa sig. En virvel kring tidsaxeln kommer att ligga i rummet men inte
nödvändigtvis i ett plan.
Tensorkalkyl
============
Vi kan,som sagt,inte omvandla energi mellan olika former enbart genom att
flytta gränserna för de mängder vi betraktar.Världen kan inte veta hur vi
hittar på att dela upp den.
När vi lägger in koordinatsystem tilldelar vi varje punkt ett läge som anges
med ett antal koordinater.På en plan karta anger vi två koordinater,i rummet
anger vi tre koordinater och om vi tar med tiden så anger vi i rum-tiden fyra
koordinater.Vi säger att kartan är tvådimensionell,rummet tredimansionellt och
rum-tiden fyrdimensionell.Läget på en karta anges med en tvådimensionell
ortsvektor (två sammanhörande tal),i rummet med en tredimensionell ortsvektor
och i rum-tiden med en fyrdimensionell ortsvektor.
Om vi ändrar koordinatsystemet ändras ortsvektorerna.Men lika lite som världen
kan veta hur vi avgränsar våra mängder kan världen veta hur vi har hittat på
att lägga in våra koordinatsystem.Det som händer i världen måste alltså vara
oberoende av hur vi väljer att lägga in koordinatsystem.Vi säger att det finns
storheter som är invarianta under koordinattransformationer.
Lägg in ett treaxligt rätlinjigt och rätvinkligt koordinatsystem i huset.Lägg
origo vid golvet i sydvästra hörnet.Lägg x-axeln mot norr,y-axeln mot öster och
z-axeln rakt upp.Gradera axlarna i meter.Häng upp en termometer på en vägg.
Termometern får då koordinater t ex (3 , 4 , 1).
Behåll origo och z-axeln men vrid x-axel och därmed även y-axeln.Termometern får
då nya koordinater t ex (2 , 4,6 , 1).
Att vi på detta sätt ändrar koordinatsystemet skall naturligtvis inte påverka vad
termometern visar.Vi säger att temperaturen är invariant under koordinattransfor-
mationer.
Även om termometern har fått nya koordinater har den inte flyttats.Inte heller
origo har flyttats.Avståndet mellan termometern och origo måste alltså vara
oförändrat.Avstånd mellan punkter är invarianta under koordinattransformationer.
I första fallet är avståndet mellan termometern och origo 5,1 m.Om vi i andra
fallet har x = 2 och z = 1 måste alltså y ha ett värde som ger avståndet 5,1.Vi
kan då beräkna y och få det till 4,6.
Vi kan alltså inte välja nya värden på x och y hur som helst.Om vi vrider x-axeln
så att vi får en ny x-koordinat kan vi beräkna värdet på motsvarande y-koordinat.
Och har vi vridit så att vi fått nytt värde på termometerns koordinater så har
alla andra koordinater ändrats på beräkningsbart sätt.Vi kan inte fritt välja men
väl beräkna nya koordinater för stolar,bord,lampor o s v.
Vi anger termometerns läge genom att ange tre koordinater.Läget anges alltså med
tre siffror.Vi säger att termometerläget är en tredimensionell vektor.I många
läroböcker använder man pilar för att beskriva vektorer.Om vi vill tänka på denna
vektor som en pil ser vi den som en pil som startar i origo och slutar vid
termometern.Längden av denna pil kallar vi termometerns avstånd från origo.Det
blir alltså 5,1 m.
Om golvets sydvästra hörn ligger 6 m åt norr,8 m åt öster och 0,5 m över tomtens
sydvästra hörn kan vi parallellförflytta koordinatsystemet från golvets sydvästra
hörn till tomtens sysdvästra hörn.Koordinataxelriktningarna ändras då inte men
x-koordinaten ökar med 6 m,y-koordinaten ökar med 8 m och z-koordinaten ökar med
0,5 m.I stället för termometerläget (3 , 4 , 1) får vi då läget (9 , 12 , 1,5).En
sådan parallellförflyttning medför också att avståndet till origo förändras.
Parallellförflyttning av koordinatsystemet innebär alltså att termometerns avstånd
från origo ändras men däremot ändras inte avståndet mellan termometern och golvets
sydvästra hörn.Koordinaterna ändras men alla avstånd mellan verkliga punkter förblir
oförändrade.Avstånd från origo är ingen invariant storhet.Det är beroende av hur
vi väljer koordinatsystem.Avståndet mellan två fysiska föremål däremot är en
invariant storhet som måste vara oberoende av hur vi väljer koordinatsystem.
Om vi bara har gjort en parallellförflyttning d v s bara har förflyttat origo
får vi direkt att alla avstånd mellan föremål blir oförändrade.När vi drar
koordinaterna för det ena föremålet från koordinaterna för det andra försvinner
origoförflyttningen.Vi har alltså räknat bort origoförflyttningen när det blir
dags att kvadrera,addera och dra roten ur för att få fram avståndet.Men om vi
har vridit koordinatsystemet eller ändrat axlarna till krokiga linjer blir det
inte lika självklart att alla avstånd mellan föremål förblir oförändrade.
Vi behöver några regler som talar om vilka storheter som förblir invarianta under
koordinattransformationer.Som kan tala om att avstånd mellan föremål förblir
invarianta medan avstånd till origo inte blir det.Vi kallar storheter som uppfyller
sådana krav för tensorer.
Betrakta ett vanligt tvådimensionellt koordinatsystem med x- och y-axel.
Lägg in ett annat koordinatsystem med samma origo men med vrid det så att
axlarna bildar vinkel med det första systemets axlar.Kalla de nya axlarna
för u- och v-axel.
Ett sätt att hantera vektorer i ett koordinatsystem är att dela upp dem
i komposanter utefter axlarna.En godtycklig vektor i x-y-systemet kan alltså
delas upp i en x-komposant och en y-komposant.
Om vi vill överföra en vektor från x-y-systemet till u-v-systemet kan vi göra
så att vi delar upp den i komposanter utefter x- och y axlarna,överför dessa
komposanter till u-v-systemet och sätter ihop vektorn i u-v-systemet.
Fig 1
Om jag i stället använder laplacetransformerna överför jag integrationen till en
multiplikation med 1/s.Jag kan nu se det som att e multipliceras med G och ger
c enligt
e(s) G(s) = c(s)
Om jag öppnar kranarna till det konstanta flödet I (liter/sek) blir
e(s) = I 1/s = I/s
eftersom laplacetransformen för 1 är 1/s.
Överföringen är en integration vilket innebär att
G(s) = 1/s
vilket ger
I 1 1
c(s) = e(s) G(s) = --- --- = I ----
s s s2
Den tidsfunktion som motsvarar laplacetransformen 1/s2 är t.Vi får
alltså
c(t) = I t
Om man multiplicerar kranflödet i liter/sek med det antal sekunder man tappar får
man alltså vattenmängden.Det inser man naturligtvis direkt men det blir inte fel om
man försöker komma fram till resultatet med hjälp av laplacetransformen.Och när
e(t) och G blir mer komplicerade blir inte slutresultatet lika självklart.
Vektoranalys
============
Om man är intresserad av vindar finns det anledning att beskriva atmosfären
på sådant sätt att man kan dra slutsatser om vilka vindar som blåser, vilka
som kommer att blåsa och vilka som har blåst.
Vind är volymflöde som orsakas av tryckskillnad. Det kan alltså vara lämpligt
att beskriva atmosfären genom att ange trycket i ett antal olika punkter.
Tryck är en endimensionell vektor, d v s en skalar. Det räcker med att ange en
enda siffra för att ange trycket i en viss punkt. Denna siffra är tryck-
skillnaden mellan punkten och en absolut nollpunkt för tryck. Tryck är alltså
en potential, d v s en skalär storhet som anges som avvikelse från en nollpunkt.
Om vi beskriver atmosfären på detta sätt säger vi att den är ett potentialfält.
Om vi vet trycket p i varje punkt kan vi rita tryckkartor där vi sammanbinder
punkter med samma tryck till isobarer. På tvådimensionella kartor blir
isobarerna linjer och i tredimensionella kartor blir isobarerna ytor.
Men det är inte tryck utan tryckskillnad som driver vind. Att vi vet trycket i
en viss punkt räcker inte för att kunna säga om vinden ökar eller minskar i
punkten. Vi behöver veta hur trycket förändras i punktens omgivning.
För att beskriva tryckförändringar i punktens omgivning lägger vi in ett
treaxligt koordinatsystem med vinkelräta axlar (x , y , z) och origo i punkten.
Så går vi ett steg i x-riktningen och mäter upp tryckändringen dpx. Vi
dividerar med steglängden dx och får ett mått dpx/dx på hur snabbt trycket
ändras i x-riktningen. Så gör vi likadant i y-riktningen och i z-riktningen och
får tre siffror som anger hur snabbt trycket ändras i området runt punkten.
Vi kan alltså beskriva tryckändringen runt punkten med tre siffror d v s med en
tredimensionell vektor. Denna vektor kallas för gradient och anges med operatorn
grad. Vi kan alltså skriva
grad p = (dpx/dx dpy/dy dpz/dz)
Gradienten för en potential d v s för en skalar är alltså en vektor som anger hur
snabbt potentialen ändras i olika riktningar.
Vind är volymflöde genom ytenhet. För att mäta vinden kan vi göra en öppning med
ytan 1 m2 och se hur många m3 som passerar genom öppningen per sekund.
Sorten för vind blir då (m3/s)/m2 = m/s alltså en hastighet som vi kallar
vindhastighet. Vi betecknar vind d v s vindhastighet med v.
Vind har inte bara ett värde den har också en riktning. Den kan alltså inte som
ses som en skalär potential utan den måste behandlas som en vektor. Vi kan t ex
ange den genom att ange vind i x-riktningen (vx), vind i y-riktningen (vy) och
vind i z-riktningen (vz). Till varje punkt i atmosfären hör alltså en skalar
som anger trycket i punkten, en vektor som anger tryckändringen i punkten
och en vektor som anger vinden i punkten.
Vind i vindriktningen kallas för vindens belopp och betecknas |v|.
Vi omsluter en punkt med en sluten yta S t ex med en klotyta. Så delar vi upp
denna yta i smådelar dS som är så små att vinden kan anses vara lika i alla
delar av en sådan småyta. |v| dS cos α är då det volymflöde som strömmar ut
genom dS (α är vinkeln mellan v och normalen till dS). På en tidsenhet bortförs
alltså via dS luftvolymen |v| dS cos α från den volym som omsluts av S. Summerar
vi över alla dS får vi den luftvolym som varje tidsenhet bortförs från volymen
inom S. För att få ett mått som inte beror på hur stor volym V som S omsluter
dividerar vi med V. Vi har nu fått ett mått på hur mycket volym (observera
skillnaden mellan omsluten volym V och den flödande luftvolym v som kan
skapas) som skapas inom S och blåser ut utan att ha blåst in. Vi har alltså
fått ett mått på punkten som vindkälla. Detta anges med operatorn div som
alltså anger källstyrka.
I många fall gäller att den vind som blåser in i en punkt är lika stor som
den vind som blåser ut från punkten. Källstyrkan är då 0 och vi säger att
vinden källfri. Men om t ex solen värmer i punkten så att luftens volym ökar
kommer större volym att lämna punkten än den volym som kom in i punkten
(eftersom luft är kompressibel kommer även tryckändring att ge volymändring).
Vi får då div v > 0.
Ett flöde (t ex vind) av något (t ex luftvolym) kan alltså beskrivas som ett
vektorfält där varje punkt tilldelas en vektor (v) som anger flödets storlek i
olika riktningar. Divergensen för denna vektor (div v) anger källstyrkan för
det som flödar.
Div v, d v s källstyrkan, är en skalär storhet.
Inom ellära använder man Kirchhoffs första lag som säger att summan av alla
strömmar till en punkt är lika med summan av alla strömmar från punkten.
Kirchhoffs första lag säger alltså att strömmen är ett källfritt flöde. Vi
har alltså div I = 0 i alla punkter. Antalet laddningsbärare, d v s antalet
elektroner, som strömmar i ledningarna och utgör det flöde som är den
elektriska strömmen ändras alltså inte i någon punkt.
Maxwells ekvationer är en annan formulering av Kirchhoffs lagar och där har
Kirchhoffs första lag formen
div I = 0
Detta gäller om inte laddningsfördelningen ändras.
Vi kan ha både vind och elektrisk ström som varierar trots att källstyrkan är
noll. Men vi kan inte ha ett nettoflöde in i eller ut ur en punkt om käll-
styrkan är noll. För källor och sänkor i ett flöde är divergensen skiljd från
noll.
Små flöden kan flyta samman till ett stort och ett stort flöde kan grena sig i
många små även om källstyrkan är noll. Att källstyrkan i en punkt är större
än noll innebär att ett flöde uppstår i punkten utan att komma in i punkten
och att källstyrkan är mindre än noll innebär att ett flöde försvinner i
punkten.
Div v ≠ 0 betyder att en del av flödet v kommer från ingenstans eller
försvinner i intet. Vi kan naturligtvis säga att ett flöde kommer från eller
försvinner till en annan dimension. Om vi t ex studerar horisontella vindar
kan vi göra det i ett tvådimensionellt system med x-axeln i öst-väst och
y-axeln i nord-syd. Om vi då har div v ≠ 0 kan vi naturligtvis skriva
div v = dvz/dz och tolka det som att en del av v kommer från eller försvinner
till en tredje dimension (z). Om vi så lägger in en vertikal axel och kallar
den för z-axeln, d v s inför den tredje dimensionen som en vertikal
dimension tolkar vi vz som fallvind eller uppvind som tillför
eller bortför horisontell vind. Om detta var hela orsaken till att div v i det
tvådimensionella systemet var skiljd från noll blir div v = 0 i det
tredimensionella systemet. Skulle det dessutom finnas andra skäl,
t ex att uppvärmning ger volymutvidgning kommer div v inte att minska
ända till noll utan ha ett restvärde som vi kan tolka som kommande från
ytterligare en dimension.
Antag att vi är intresserade av en viss punkt A. Vi lägger in en plan yta
som innehåller A. Så går vi runt en sluten väg runt A i ytan. För varje steg
vi tar multiplicerar vi steglängden med vindhastigheten i stegriktningen.
Alla dessa produkter adderar vi tills vi är tillbaka till utgångspunkten. Vi
bildar alltså
S
∫ v dl
L
där
dl är steglängden och L betecknar en sluten väg
Värdet av denna integral beror på hur vi valt att lägga planet. Vi väljer så
det plan som ger maximalt värde på denna integral. Så dividerar vi med
den ytan som gångvägen omsluter och kallar det vi då får fram för beloppet
av rot v.
Om vi får lika mycket medvind som motvind när vi går runt en sluten väg är
rot v = 0. Vi säger då att vinden är virvelfri. Skulle det däremot blåsa en
virvelvind runt A kan vi följa med virveln och gå runt A så att vi hela vägen
får medvind. Vi beskriver detta med en vektor som kallas rot v som har
beloppet lika med ovanstående integral dividerad med den omslutna ytan
och riktningen sammanfallande med normalen till den omslutna ytan.
Ett exempel på ett praktiskt taget virvelfritt fält är gravitationen vid
markytan. Antag att vi går runt en sluten väg och för varje steg
multiplicerar tyngden med höjdändringen. När vi kommer tillbaka till
utgångspunkten och lägger ihop alla dessa produkter får vi det arbete
som uträttats under vägen och detta blir alltid noll hur vi än går. Det i
sin tur innebär att arbetet som uträttas när vi går från punkt A till punkt B
blir lika stort vilken väg vi än går. Vi kan då tilldela punkt A en potential
gA som motsvarar arbetet att föra en massenhet från en
referenspunkt till A. Och på motsvarande sätt kan vi tilldela punkt B en
potential gB. Arbetet att föra massan m från A till B blir
då W enligt
W = m gA - m gB = m (gA - gB)
Inom ellära använder man Kirchhoffs andra lag som säger att summan
av alla spänningar längs en sluten väg är noll, d v s att fältstyrkan är
virvelfri.
I Maxwells ekvationer har Kirchhoffs andra lag formuleringen
rot E = 0
(OBS att E här betyder elektrisk fältstyrka, inte energi)
Detta gäller om det inte finns några varierande magnetiska fält. Tids-
derivatan hos ett magnetiskt fält ger elektriska virvlar.
I ett tredimensionellt system är vi vana vid att se virvlar. Vi har alla sett
virvelvindar och virvlar när vattnet runner ur badkaret. I tre dimensioner
kan vi göra en uppdelning i ett plan och en axel vinkelrät mot planet. En
virvel runt denna axel kommer då att ligga i planet. För ett fyrdimensionellt
system tillkommer emellertid möjligheter som inte är helt lätta att före-
ställa sig. En virvel kring tidsaxeln kommer att ligga i rummet men inte
nödvändigtvis i ett plan.
Tensorkalkyl
============
Vi kan,som sagt,inte omvandla energi mellan olika former enbart genom att
flytta gränserna för de mängder vi betraktar.Världen kan inte veta hur vi
hittar på att dela upp den.
När vi lägger in koordinatsystem tilldelar vi varje punkt ett läge som anges
med ett antal koordinater.På en plan karta anger vi två koordinater,i rummet
anger vi tre koordinater och om vi tar med tiden så anger vi i rum-tiden fyra
koordinater.Vi säger att kartan är tvådimensionell,rummet tredimansionellt och
rum-tiden fyrdimensionell.Läget på en karta anges med en tvådimensionell
ortsvektor (två sammanhörande tal),i rummet med en tredimensionell ortsvektor
och i rum-tiden med en fyrdimensionell ortsvektor.
Om vi ändrar koordinatsystemet ändras ortsvektorerna.Men lika lite som världen
kan veta hur vi avgränsar våra mängder kan världen veta hur vi har hittat på
att lägga in våra koordinatsystem.Det som händer i världen måste alltså vara
oberoende av hur vi väljer att lägga in koordinatsystem.Vi säger att det finns
storheter som är invarianta under koordinattransformationer.
Lägg in ett treaxligt rätlinjigt och rätvinkligt koordinatsystem i huset.Lägg
origo vid golvet i sydvästra hörnet.Lägg x-axeln mot norr,y-axeln mot öster och
z-axeln rakt upp.Gradera axlarna i meter.Häng upp en termometer på en vägg.
Termometern får då koordinater t ex (3 , 4 , 1).
Behåll origo och z-axeln men vrid x-axel och därmed även y-axeln.Termometern får
då nya koordinater t ex (2 , 4,6 , 1).
Att vi på detta sätt ändrar koordinatsystemet skall naturligtvis inte påverka vad
termometern visar.Vi säger att temperaturen är invariant under koordinattransfor-
mationer.
Även om termometern har fått nya koordinater har den inte flyttats.Inte heller
origo har flyttats.Avståndet mellan termometern och origo måste alltså vara
oförändrat.Avstånd mellan punkter är invarianta under koordinattransformationer.
I första fallet är avståndet mellan termometern och origo 5,1 m.Om vi i andra
fallet har x = 2 och z = 1 måste alltså y ha ett värde som ger avståndet 5,1.Vi
kan då beräkna y och få det till 4,6.
Vi kan alltså inte välja nya värden på x och y hur som helst.Om vi vrider x-axeln
så att vi får en ny x-koordinat kan vi beräkna värdet på motsvarande y-koordinat.
Och har vi vridit så att vi fått nytt värde på termometerns koordinater så har
alla andra koordinater ändrats på beräkningsbart sätt.Vi kan inte fritt välja men
väl beräkna nya koordinater för stolar,bord,lampor o s v.
Vi anger termometerns läge genom att ange tre koordinater.Läget anges alltså med
tre siffror.Vi säger att termometerläget är en tredimensionell vektor.I många
läroböcker använder man pilar för att beskriva vektorer.Om vi vill tänka på denna
vektor som en pil ser vi den som en pil som startar i origo och slutar vid
termometern.Längden av denna pil kallar vi termometerns avstånd från origo.Det
blir alltså 5,1 m.
Om golvets sydvästra hörn ligger 6 m åt norr,8 m åt öster och 0,5 m över tomtens
sydvästra hörn kan vi parallellförflytta koordinatsystemet från golvets sydvästra
hörn till tomtens sysdvästra hörn.Koordinataxelriktningarna ändras då inte men
x-koordinaten ökar med 6 m,y-koordinaten ökar med 8 m och z-koordinaten ökar med
0,5 m.I stället för termometerläget (3 , 4 , 1) får vi då läget (9 , 12 , 1,5).En
sådan parallellförflyttning medför också att avståndet till origo förändras.
Parallellförflyttning av koordinatsystemet innebär alltså att termometerns avstånd
från origo ändras men däremot ändras inte avståndet mellan termometern och golvets
sydvästra hörn.Koordinaterna ändras men alla avstånd mellan verkliga punkter förblir
oförändrade.Avstånd från origo är ingen invariant storhet.Det är beroende av hur
vi väljer koordinatsystem.Avståndet mellan två fysiska föremål däremot är en
invariant storhet som måste vara oberoende av hur vi väljer koordinatsystem.
Om vi bara har gjort en parallellförflyttning d v s bara har förflyttat origo
får vi direkt att alla avstånd mellan föremål blir oförändrade.När vi drar
koordinaterna för det ena föremålet från koordinaterna för det andra försvinner
origoförflyttningen.Vi har alltså räknat bort origoförflyttningen när det blir
dags att kvadrera,addera och dra roten ur för att få fram avståndet.Men om vi
har vridit koordinatsystemet eller ändrat axlarna till krokiga linjer blir det
inte lika självklart att alla avstånd mellan föremål förblir oförändrade.
Vi behöver några regler som talar om vilka storheter som förblir invarianta under
koordinattransformationer.Som kan tala om att avstånd mellan föremål förblir
invarianta medan avstånd till origo inte blir det.Vi kallar storheter som uppfyller
sådana krav för tensorer.
Betrakta ett vanligt tvådimensionellt koordinatsystem med x- och y-axel.
Lägg in ett annat koordinatsystem med samma origo men med vrid det så att
axlarna bildar vinkel med det första systemets axlar.Kalla de nya axlarna
för u- och v-axel.
Ett sätt att hantera vektorer i ett koordinatsystem är att dela upp dem
i komposanter utefter axlarna.En godtycklig vektor i x-y-systemet kan alltså
delas upp i en x-komposant och en y-komposant.
Om vi vill överföra en vektor från x-y-systemet till u-v-systemet kan vi göra
så att vi delar upp den i komposanter utefter x- och y axlarna,överför dessa
komposanter till u-v-systemet och sätter ihop vektorn i u-v-systemet.


 Och hela vektorn i u-v-systemet blir
A = Au + Av (vektoriell addition)
Så länge vi bara sysslar med tvådimensionella koordinatsystem går det ju att
använda olika bokstäver (x , y ,u , v) för de olika axlarna.Men när man vill
studera mångdimensionella system blir det problem att benämna axlarna på detta
sätt.Inom tensoranalys använder man därför ett annat system för axelbenämning.
Inom tensoranalys ersätter man index och exponent med subscript och superscript
(jag använder de engelska benämningarna för jag har inte funnit några svenska).
x2 betyder alltså inte "x upphöjt till två" utan koordinataxel nr 2 alltså
vanligen y-axeln.I ett koordinatsystem med N axlar benämner man alltså axlarna xj
där j går från 1 till N.
Om vi kallar Ax för A1 , Ay för A2 , Au för A1 och Av för A2
kan vi skriva ovanstående uttryck för komposanter i u-v-systemet som
Och hela vektorn i u-v-systemet blir
A = Au + Av (vektoriell addition)
Så länge vi bara sysslar med tvådimensionella koordinatsystem går det ju att
använda olika bokstäver (x , y ,u , v) för de olika axlarna.Men när man vill
studera mångdimensionella system blir det problem att benämna axlarna på detta
sätt.Inom tensoranalys använder man därför ett annat system för axelbenämning.
Inom tensoranalys ersätter man index och exponent med subscript och superscript
(jag använder de engelska benämningarna för jag har inte funnit några svenska).
x2 betyder alltså inte "x upphöjt till två" utan koordinataxel nr 2 alltså
vanligen y-axeln.I ett koordinatsystem med N axlar benämner man alltså axlarna xj
där j går från 1 till N.
Om vi kallar Ax för A1 , Ay för A2 , Au för A1 och Av för A2
kan vi skriva ovanstående uttryck för komposanter i u-v-systemet som
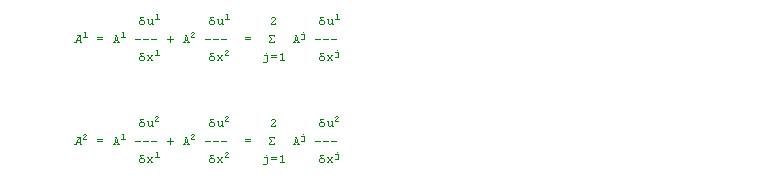 Nu närmar vi oss quintessensen av tensoranalysen.För det är nu mycket lätt att
generalisera denna transformation till att gälla för hur många dimensioner som helst.
En transformation från ett x-system med N dimensioner till ett u-system med N
dimensioner gör man tydligen så att u-systemets komposanter blir
Nu närmar vi oss quintessensen av tensoranalysen.För det är nu mycket lätt att
generalisera denna transformation till att gälla för hur många dimensioner som helst.
En transformation från ett x-system med N dimensioner till ett u-system med N
dimensioner gör man tydligen så att u-systemets komposanter blir
 Genom att låta p gå från 1 till N får man då alla N komposanterna i u-systemet och
kan addera dem (vektoriellt) till den transformerade vektorn.
Att man kan skriva som efter sista likhetstecknet i uttrycket ovan beror på att man
inom tensoranalys använder en regel som säger att om samma superscript eller subscript
förekommer två gånger i samma term så skall man summera för alla värden på detta från
1 till N (summakonventionen).Eftersom j förekommer på två ställen skall man alltså
summera för j=1 till N.
Om en storhet transformeras enligt denna ekvation kallas den en tensor.
j förekommer här i nämnaren på differentialuttrycket.En tensor där summationsscriptet
förekommer i nämnaren på differentialuttrycket kallas contravariant.Om det finns i
täljaren kallas tensorn covariant.Man använder superscript för att ange element
av en contravariant tensor och subscript för att ange element av en covariant
tensor.Hanteringen av superscript och subscript är en viktig del av tensoranalysen.
Många operationer med tensorer kan göras enbart genom att man använder räkneregler
som gäller för tensorernas superscript och subscript.
Enkla siffervärden (skalarer) som temperatur transformeras direkt mellan koordinat-
system utan att några komposanter ändras.Sådana värden kallas för tensorer av nollte
ordningen.Vanliga vektorer får nya axelkomposanter när de transformeras till nya
koordinatsystem.De kallas för tensorer av första ordningen.
Exempel på tensorer av första ordningen är hastighet (definierad som lägesförändring
per parametertid) och avstånd mellan föremål.
I den gröna texten har jag försökt beskriva hur man kommer fram till vad en
tensor är.Jag har där bara sett på vridning av koordinatsystem med räta linjer
som axlar men en poäng med tensoranalysen är att den gäller även för andra typer
av koordinatsystem.Vi kan ha cylindriska eller sfäriska system eller system med
krokiga axlar t ex hyperbler.
Och den kanske viktigaste användningen har varit inom relativitetsteori eftersom
den medger att man arbetar med fyra (eller fler) dimensioner.De regler som gäller
för hantering av tensorer går alltså att använda när man försöker ställa upp
samband i den fyrdimensionella rum-tiden.
Genom att låta p gå från 1 till N får man då alla N komposanterna i u-systemet och
kan addera dem (vektoriellt) till den transformerade vektorn.
Att man kan skriva som efter sista likhetstecknet i uttrycket ovan beror på att man
inom tensoranalys använder en regel som säger att om samma superscript eller subscript
förekommer två gånger i samma term så skall man summera för alla värden på detta från
1 till N (summakonventionen).Eftersom j förekommer på två ställen skall man alltså
summera för j=1 till N.
Om en storhet transformeras enligt denna ekvation kallas den en tensor.
j förekommer här i nämnaren på differentialuttrycket.En tensor där summationsscriptet
förekommer i nämnaren på differentialuttrycket kallas contravariant.Om det finns i
täljaren kallas tensorn covariant.Man använder superscript för att ange element
av en contravariant tensor och subscript för att ange element av en covariant
tensor.Hanteringen av superscript och subscript är en viktig del av tensoranalysen.
Många operationer med tensorer kan göras enbart genom att man använder räkneregler
som gäller för tensorernas superscript och subscript.
Enkla siffervärden (skalarer) som temperatur transformeras direkt mellan koordinat-
system utan att några komposanter ändras.Sådana värden kallas för tensorer av nollte
ordningen.Vanliga vektorer får nya axelkomposanter när de transformeras till nya
koordinatsystem.De kallas för tensorer av första ordningen.
Exempel på tensorer av första ordningen är hastighet (definierad som lägesförändring
per parametertid) och avstånd mellan föremål.
I den gröna texten har jag försökt beskriva hur man kommer fram till vad en
tensor är.Jag har där bara sett på vridning av koordinatsystem med räta linjer
som axlar men en poäng med tensoranalysen är att den gäller även för andra typer
av koordinatsystem.Vi kan ha cylindriska eller sfäriska system eller system med
krokiga axlar t ex hyperbler.
Och den kanske viktigaste användningen har varit inom relativitetsteori eftersom
den medger att man arbetar med fyra (eller fler) dimensioner.De regler som gäller
för hantering av tensorer går alltså att använda när man försöker ställa upp
samband i den fyrdimensionella rum-tiden.