Leif Andersson Henriksbergsvägen 104 136 67 Vendelsö 2008-09-21
Tensorer
========
Om jag skall segla på Skagerack vill jag veta så mycket som möjligt om atmosfären vid
Skageracks yta. För det behöver jag ett koordinatsystem. Eftersom jag bara är intresserad
av förhållandena vid den nästan plana havsytan räcker det med ett rätlinjigt, tvådimensionellt
och ortogonalt koordinatsystem (kartesiskt koordinatsystem) med en x-axel och en vinkelrät
y-axel. Jag låter y-axeln peka mot norr och x-axeln mot väster.
För varje punkt i detta koordinatsystem kan jag ange temperatur, lufttryck och en
vindhastighetsvektor.
Temperatur anges med en siffra som anger avvikelse från en nollpunkt. Storheter av denna typ
kallas potential. Även lufttrycket är en potential. Temperaturfördelningen och
lufttrycksfördelningen över koordinatsystemet är två exempel på potentialfält.
När det gäller vindhastighet räcker det inte med en siffra. Jag vill veta både hastighet och
riktning. För det behövs två siffror, till exempel hastighet i x-led och hastighet i y-led.
Vindhastighet över koordinatsystemet är ett exempel på ett vektorfält.
Jag kan naturligtvis ändra på koordinatsystemet, till exempel vrida det så att y-axeln pekar
åt väster. Det innebär att punkter på havsytan får nya koordinater men det påverkar
naturligtvis varken temperatur, lufttryck eller vindhastighet. Om jag vet hur potentialfält och
vektorfält ser ut innan jag ändrar koordinatsystemet måste jag kunna transformera dem till
det nya koordinatsystemet.
Storheter som kan transformeras mellan olika koordinatsystem kallas tensorer och regler för
hur man gör detta kallas för tensoranalys.
När jag vill ha en beskrivning över Skagerack ligger det nära till hands att transformera till ett
koordinatsystem med en skala som gör att det kan avbildas på en hanterlig karta. Jag kan till
exempel välja en karta i skala 1:1000 vilket innebär att 1 m i verkligheten är 1 mm på kartan.
Kartans skala är alltså 1/1000 = 0,001.
När det gäller temperatur och lufttryck är värdet i verkligheten samma som värdet på kartan.
Om temperaturen på en viss kobbe är 23 oC i verkligheten skall den vara 23 oC även på samma kobbe
på kartan. Man säger att potential är en skalar som är invariant under koordinattransformationer.
Men vindhastigheten blir olika i verkligheten och på kartan. Om det i verkligheten blåser 2 m/s
i x-riktningen och 3 m/s i y-riktningen blir det på kartan 0,001*2 = 0,002 m/s =2 mm/s i x-riktningen
och 0.001*3 = 0,003 m/s = 3 mm/s i y-riktningen
För vindhastigheten gäller alltså att den transformeras från verkligheten till kartan genom att
dess komposanter multipliceras med skalan (1/1000). En vektor som transformeras på detta sätt
kallas för en kontravariant vektor eller en kontravariant tensor.
Vindar beror på skillnader i lufttryck. Det blåser från högtryck in mot lågtryck. Om jag har en karta
som anger lufttryck har jag alltså en karta som visar de tryckskillnader som driver vindarna. Ofta
blåser vindar i korta byar och ett studium av tryckskillnader kan ge en bättre bild av vindförhållanden
än vindmätning i ett visst ögonblick. Men det är inte tryck utan tryckskillnad, det vill säga
tryckgradient, som driver vind. För att bestämma tryckgradienten går man ett steg i x-riktningen
och noterar hur mycket trycket ändrats. då dividerar man med steglängden och har därmed fått
tryckgradientens x-komposant. Och så gör man likadant i y-riktningen.
Den vinddrivande tryckgradienten är alltså en vektor med en x-komposant och en y-komposant
som har sorten Pa/m. Om tryckgradientens x-komposant är 6 Pa/m och y-komposant 4 Pa/m i
verkligheten är x-komposanten på kartan (1/0,001)*6 = 6000 Pa/m = 6 Pa/mm och y-komposant
(1/0,001)*4 = 4000 Pa/m = 4 Pa/mm.
För tryckgradienten gäller alltså att den transformeras från från verkligheten till kartan genom
division med skalan (= multiplikation med inverterade värdet av skalan, det vill säga med 1000).
En vektor som transformeras på detta sätt kallas för en kovariant vektor eller kovariant tensor.
En kontravariant tensor är alltså proportionell mot skalan när det transformeras från verkligheten
till kartan. En kovariant tensor är omvänt proportionell mot skalan när den transformeras från
verkligheten till kartan.
( Stavelserna ko och kontra kommer av att man tänker sig enhetsvektorer. I verkligheten är en
enhetsvektor en meter lång så att verklighetens längdenhet gånger enhetsvektorn blir en meter.
I skala 1/1000 är enhetsvektorn 1000 meter så att kartans millimeterlånga längdenhet gånger
enhetsvektorn blir en meter. Ko kommer av att den transformerade vektorns längd ökar när
enhetsvektorn ökar, kontra av att den transformerade vektorns längd minskar när enhetsvektorn
ökar.)
För att hålla isär verklighetens och kartans koordinatsystem kallar jag verklighetens för (x, y) och
kartans för (x', y'). Om jag betecknar vindhastighetsvektorn med A kan jag dela upp den i
x-komposant (Ax) och y-komposant (Ay) och skriva
A = Ax x + Ay y
där x och y är enhetsvektorer i x-riktningen och y-riktningen. På kartan får jag då
A' = A'x x' + A'y y'
Om kartans axlar är parallella med verklighetens gäller då att
A'x = 0,001* Ax
A'y = 0,001* Ay
Om jag inte vet skalan och inte vet om det är samma skala i y-riktningen som i x-riktningen kan
jag mäta upp en liten sträcka (∂x) i x-riktningen och mäta upp motsvarande sträcka på
kartan (∂x'). Jag får då skalan i x-riktningen som ∂x'/∂x och på motsvarande sätt får jag skalan,
det vill säga skalfaktorn, i y-led som ∂y'/∂y. Det ger för den kontravarianta vektorn A
A'x = Ax ∂x'/∂x
A'y = Ay ∂y'/∂y
Om jag betecknar tryckgradienten med B skall jag inte multiplicera med skalan utan med inverterade
värdet av skalan när jag transformerar B från verkligheten till kartan. Det ger för den kovarianta
vektorn B
B'x = Bx ∂x/∂x'
B'y = By ∂x/∂y'
Tensoranalys utvecklades som ett sätt att hålla reda på alla komponenterna vid mångdimensionella
koordinattransformationer. Att benämna koordinataxlarna x, y, z, t och så vidare fungerar vid ett
fåtal dimensioner men för att hantera obegränsat antal dimensioner behöver man ett annat
benämningssätt.
Inom tensoranalys hanterar man enbart linjära transformationer och har därför sällan behov av
exponenter. Man kan därför använda index i form av superscript eller subscript. I ett
N-dimensionellt system kan man då benämna axlarna x1, x2,... xN där 1, 2, .... N inte är
exponenter utan superscript.
I stället för att kalla axlarna på mitt koordinatsystem för x och y kallar jag dem då x1
och x2. Och jag kan döpa om Bx till B1 och By till B2. Det här benämningsättet ger också ett sätt
att hålla reda på kontravarianta och kovarianta tensorer. För att visa att vindhastighet är en
kontravariant tensor döper jag om Ax till A1 och Ay till A2. Jag använder alltså superscript för
kontravariant tensor och jag använder subscript för kovariant tensor. Och jag döper A:s
komposanter till Ap och B:s komposanter till Bp. Och jag använder ordet index som en sammanfattande
benämning på superscript och subscript.
Hur blir det om jag vrider kartans koordinatsystem? Om jag använder en karta som inte har norr
uppåt utan till exempel nordväst.
Om kartans och verklighetens koordinataxlar är parallella motsvarar en förflyttning i
x2-riktningen i verkligheten enbart en förflyttning i x'2-riktningen på kartan. Förflyttningen
i x'1-riktningen blir noll. Det vill säga att
∂x'1
---- = 0
∂x2
När jag vrider kartans koordinatsystem minskar beloppet av ∂x'1/∂x1 och ∂x'1/∂x2 får ett värde
som inte längre är noll. Det ger för en kontravariant tensor
∂x'1 ∂x'1
A'1 = ---- A1 + ---- A2 = a11A1 + a12A2
∂x1 ∂x2
∂x'2 ∂x'2
A'2 = ---- A1 + ---- A2 = a21A1 + a22A2
∂x1 ∂x2
Och för en kovariant tensor
∂x1 ∂x2
B'1 = ---- B1 + ---- B2 = b11B1 + b21B2
∂x'1 ∂x'1
∂x1 ∂x2
B'2 = ---- B1 + ---- B2 = b21B1 + b22B2
∂x'2 ∂x'2
Fär ett godtyckligt antal (N) dimensioner kan detta generaliseras till att den kontravarianta
utgångstensorn Aq transformeras till måltensorn Ap enligt
N
Ap = Σ apq Aq
q=1
och att den kovarianta utgångstensorn Bq transformeras till måltensorn Bp enligt
N
Bp = Σ bpq Bq
q=1
För en person som ägnar dagarna åt att skriva denna typ av summor ligger det nära till hands
att fråga sig om det inte finns enklare skrivsätt som inte riskerar att misstolkas. Detta ledde
till summakonventionen som säger att om ett index upprepas i en term skall man summera över
detta index. Det gör att ovanstående summor kan skrivas
Ap = apq Aq
och
Bp = bpq Bq
En skalar, till exempel en potential som temperatur, är invariant under koordinattranformationer.
En sådan storhet kallas för tensor av nollte ordningen eller en tensor av rank = 0.
En vektor, till exempel vindhastighet eller tryckgradient, kallas för en tensor av första ordningen
eller för en tensor av rank = 1. Vindhastighet Aq kallas för en kontravariant tensor och
tryckgradient Bq kallas för en kovariant tensor.
Skalfaktorerna apq för transformation av en kontravariant tensor kallas för en tensor av andra
ordningen eller en tensor av rank = 2. Den är kontravariant med avseende på p och kovariant
med avseende på q och kallas därför för en blandad (mixed) tensor.
Tensoranalys utvecklades för att man behövde ett sätt att hantera transformationer mellan
mångdimensionella system med olika slags axlar. Bland annat behövde man för relativitetsteorin
ett sätt att hantera fyrdimensionella system med icke-vinkelräta, krokiga axlar. Men i många
fall behöver man transformera mellan rätvinkliga, ortogonala system i skala 1:1. Det handlar
då om att transformera mellan system med vridning och eller flyttat origo. Tensorer för denna
typ av transformationer kallas kartesiska tensorer.
En viktig förenkling som gäller för kartesiska tensorer är att det inte är någon skillnad mellan
kontravarianta och kovarianta tensorer. Om man markerar målsystemet med ' skall man vid
kontravariant tensor bestämma skalfaktorn för x'1 till ∂x'1/∂x1. Man tar alltså ett steg ∂x1
i x1-riktningen i utgångstystemet, ser vad set motsvarar i målsystemet ∂x'1 och dividerar med
∂x1. Men för en kovariant tensor bestämmer man skalfaktorn för ∂x'1 till ∂x1/∂x'1. Man tar alltså
ett steg ∂x'1 i målsystemet, ser vad det motsvarar i utgångsystemet ∂x1 och dividerar med ∂x'1.
Om skalan är 1:1 gäller att
∂x'1 ∂x1
----- = ----- = cos α
∂x1 ∂x'1
där α är vinkeln mellan x1-axeln och x'1-axeln. Kontravariant transformation ger då samma resultat
som kovariant.
Tensorer skrivs ibland i matrisform. Transformationen av den fyrdimensionella kontravarianta
kolumnvektorn Aq till målvektorn A'p det vill säga
A'p = apq Aq
blir i matrisform
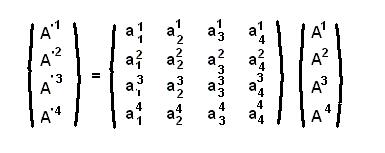 En blandad tensor av andra ordningen där elementen i huvuddiagonalen är 1 och alla övriga
element är noll kallas kroneckers delta δpq. Denna tensor definieras alltså som
1 för p=q
δpq =
0 för p≠q
Även den kontravarianta tensorn δpq och den kovarianta tensorn δpq brukar kallas kroneckers
delta och definieras på samma sätt.
För att kunna beskriva min omgivning kan jag lägga upp ett rätlinjigt,ortogonalt och
fyrdimensionellt koordinatsystem med mig i origo. Jag kan välja axlarna så att det får tre
rumsaxlar och en koordinattidsaxel. Det gör jag genom att lägga det så att när parametertiden
ökar så ökar koordinattiden medan de flesta rumskoordinater förblir oförändrade. Jag kan kalla
x2-axeln för koordinattidsaxel.
Antag att ett rymdskepp passerar mig med en rumshastighet i x1-riktningen. Besättningen
på rymdskeppet ser på världen med sitt koordinatsystem med rymdskeppet i origo och med
koordinattidsaxeln riktad så att de flesta föremål ombord på skeppet står stilla i rummet.
Hur ser min värld ut i besättningens koordinatsystem? Hur transformeras mitt rätvinkliga
ortogonala koordinatsystem till besättningens rätvinkliga ortogonala koordinatsystem?
För transformation mellan koordinatsystem i skala 1:1 med rätlinjiga ortogonala axlar gäller
att skalfaktorerna skall uppfylla ortogonalitetsvillkoret
a pr a rq = δ pq
där a pr är skalfaktorerna för transformation från utgångsystemet till målsystemet och a rq
är skalfaktorerna för transformation från målsystemet till utgångsystemet.
När parametertiden ökar flyttar jag mig i min koordinattidsriktning x2 och besättningen
flyttar sig i sin koordinattidsriktning x'2 där vinkeln mellan x2 och x'2 är α och
sin α = v där v är rymdskeppets rumshastighet. Transformationsmatrisen för kontravariant
transformation blir då
En blandad tensor av andra ordningen där elementen i huvuddiagonalen är 1 och alla övriga
element är noll kallas kroneckers delta δpq. Denna tensor definieras alltså som
1 för p=q
δpq =
0 för p≠q
Även den kontravarianta tensorn δpq och den kovarianta tensorn δpq brukar kallas kroneckers
delta och definieras på samma sätt.
För att kunna beskriva min omgivning kan jag lägga upp ett rätlinjigt,ortogonalt och
fyrdimensionellt koordinatsystem med mig i origo. Jag kan välja axlarna så att det får tre
rumsaxlar och en koordinattidsaxel. Det gör jag genom att lägga det så att när parametertiden
ökar så ökar koordinattiden medan de flesta rumskoordinater förblir oförändrade. Jag kan kalla
x2-axeln för koordinattidsaxel.
Antag att ett rymdskepp passerar mig med en rumshastighet i x1-riktningen. Besättningen
på rymdskeppet ser på världen med sitt koordinatsystem med rymdskeppet i origo och med
koordinattidsaxeln riktad så att de flesta föremål ombord på skeppet står stilla i rummet.
Hur ser min värld ut i besättningens koordinatsystem? Hur transformeras mitt rätvinkliga
ortogonala koordinatsystem till besättningens rätvinkliga ortogonala koordinatsystem?
För transformation mellan koordinatsystem i skala 1:1 med rätlinjiga ortogonala axlar gäller
att skalfaktorerna skall uppfylla ortogonalitetsvillkoret
a pr a rq = δ pq
där a pr är skalfaktorerna för transformation från utgångsystemet till målsystemet och a rq
är skalfaktorerna för transformation från målsystemet till utgångsystemet.
När parametertiden ökar flyttar jag mig i min koordinattidsriktning x2 och besättningen
flyttar sig i sin koordinattidsriktning x'2 där vinkeln mellan x2 och x'2 är α och
sin α = v där v är rymdskeppets rumshastighet. Transformationsmatrisen för kontravariant
transformation blir då
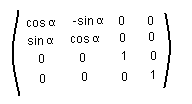 När man inte insåg skillnaden mellan parametertid och koordinattid trodde man att
transformationen måste ge oförändrad ljushastighet. En transform som uppfyller det kravet
är Lorentztransformen med transformationsmatrisen
När man inte insåg skillnaden mellan parametertid och koordinattid trodde man att
transformationen måste ge oförändrad ljushastighet. En transform som uppfyller det kravet
är Lorentztransformen med transformationsmatrisen
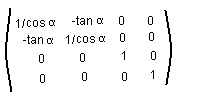 Men denna uppfyller inte ortogonalitetsvillkoret. Den transformerar alltså inte från mitt
till besättningens koordinatsystem.
Lorentztransformationen transformerar alltså inte till besättningens koordinatsystem utan
till en bild som jag gör. Det påminner om att jag ritar en perspektivbild som bara liknar
verkligheten sedd från min utgångspunkt.
När det gäller transform mellan mitt och besättningens koordinatsystem finns det två viktiga
aspekter att tänka på.
Den första är att mitt koordinatsystem beskriver en qvaolym där bara en liten del har någon
koppling till mitt medvetande. För mig finns vid en viss parametertid bara det som finns i min
egoqvaolym, i mitt påverkansnu, i mitt samtidsnu och i mitt observationsnu. Resten av världen
kan jag varken se eller påverka. Och i besättningens koordinatsystem har inte bara koordinaterna
ändrats, även påverkansnu, samtidsnu och observationsnu har ändrats. Besättningen kan alltså
se och påverka en del av världen som är oåtkomlig för mig.
Den andra aspekten är att jag måste accelerera om jag vill komma ombord på rymdskeppet.
För att komma från mitt till besättningens koordinatsystem måste jag alltså gå mot ett
gravitationsfält. Det innebär att min gravitationshöjd ökar. Ökad gravitationshöjd innebär att
ljushastigheten ökar vilket innebär ändrad skala. Man får alltså en skaländring på liknande
sätt som när man på en karta enligt Mercators projektion flyttar sig mot polen.
Men denna uppfyller inte ortogonalitetsvillkoret. Den transformerar alltså inte från mitt
till besättningens koordinatsystem.
Lorentztransformationen transformerar alltså inte till besättningens koordinatsystem utan
till en bild som jag gör. Det påminner om att jag ritar en perspektivbild som bara liknar
verkligheten sedd från min utgångspunkt.
När det gäller transform mellan mitt och besättningens koordinatsystem finns det två viktiga
aspekter att tänka på.
Den första är att mitt koordinatsystem beskriver en qvaolym där bara en liten del har någon
koppling till mitt medvetande. För mig finns vid en viss parametertid bara det som finns i min
egoqvaolym, i mitt påverkansnu, i mitt samtidsnu och i mitt observationsnu. Resten av världen
kan jag varken se eller påverka. Och i besättningens koordinatsystem har inte bara koordinaterna
ändrats, även påverkansnu, samtidsnu och observationsnu har ändrats. Besättningen kan alltså
se och påverka en del av världen som är oåtkomlig för mig.
Den andra aspekten är att jag måste accelerera om jag vill komma ombord på rymdskeppet.
För att komma från mitt till besättningens koordinatsystem måste jag alltså gå mot ett
gravitationsfält. Det innebär att min gravitationshöjd ökar. Ökad gravitationshöjd innebär att
ljushastigheten ökar vilket innebär ändrad skala. Man får alltså en skaländring på liknande
sätt som när man på en karta enligt Mercators projektion flyttar sig mot polen.
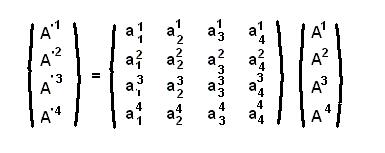 En blandad tensor av andra ordningen där elementen i huvuddiagonalen är 1 och alla övriga
element är noll kallas kroneckers delta δpq. Denna tensor definieras alltså som
1 för p=q
δpq =
0 för p≠q
Även den kontravarianta tensorn δpq och den kovarianta tensorn δpq brukar kallas kroneckers
delta och definieras på samma sätt.
För att kunna beskriva min omgivning kan jag lägga upp ett rätlinjigt,ortogonalt och
fyrdimensionellt koordinatsystem med mig i origo. Jag kan välja axlarna så att det får tre
rumsaxlar och en koordinattidsaxel. Det gör jag genom att lägga det så att när parametertiden
ökar så ökar koordinattiden medan de flesta rumskoordinater förblir oförändrade. Jag kan kalla
x2-axeln för koordinattidsaxel.
Antag att ett rymdskepp passerar mig med en rumshastighet i x1-riktningen. Besättningen
på rymdskeppet ser på världen med sitt koordinatsystem med rymdskeppet i origo och med
koordinattidsaxeln riktad så att de flesta föremål ombord på skeppet står stilla i rummet.
Hur ser min värld ut i besättningens koordinatsystem? Hur transformeras mitt rätvinkliga
ortogonala koordinatsystem till besättningens rätvinkliga ortogonala koordinatsystem?
För transformation mellan koordinatsystem i skala 1:1 med rätlinjiga ortogonala axlar gäller
att skalfaktorerna skall uppfylla ortogonalitetsvillkoret
a pr a rq = δ pq
där a pr är skalfaktorerna för transformation från utgångsystemet till målsystemet och a rq
är skalfaktorerna för transformation från målsystemet till utgångsystemet.
När parametertiden ökar flyttar jag mig i min koordinattidsriktning x2 och besättningen
flyttar sig i sin koordinattidsriktning x'2 där vinkeln mellan x2 och x'2 är α och
sin α = v där v är rymdskeppets rumshastighet. Transformationsmatrisen för kontravariant
transformation blir då
En blandad tensor av andra ordningen där elementen i huvuddiagonalen är 1 och alla övriga
element är noll kallas kroneckers delta δpq. Denna tensor definieras alltså som
1 för p=q
δpq =
0 för p≠q
Även den kontravarianta tensorn δpq och den kovarianta tensorn δpq brukar kallas kroneckers
delta och definieras på samma sätt.
För att kunna beskriva min omgivning kan jag lägga upp ett rätlinjigt,ortogonalt och
fyrdimensionellt koordinatsystem med mig i origo. Jag kan välja axlarna så att det får tre
rumsaxlar och en koordinattidsaxel. Det gör jag genom att lägga det så att när parametertiden
ökar så ökar koordinattiden medan de flesta rumskoordinater förblir oförändrade. Jag kan kalla
x2-axeln för koordinattidsaxel.
Antag att ett rymdskepp passerar mig med en rumshastighet i x1-riktningen. Besättningen
på rymdskeppet ser på världen med sitt koordinatsystem med rymdskeppet i origo och med
koordinattidsaxeln riktad så att de flesta föremål ombord på skeppet står stilla i rummet.
Hur ser min värld ut i besättningens koordinatsystem? Hur transformeras mitt rätvinkliga
ortogonala koordinatsystem till besättningens rätvinkliga ortogonala koordinatsystem?
För transformation mellan koordinatsystem i skala 1:1 med rätlinjiga ortogonala axlar gäller
att skalfaktorerna skall uppfylla ortogonalitetsvillkoret
a pr a rq = δ pq
där a pr är skalfaktorerna för transformation från utgångsystemet till målsystemet och a rq
är skalfaktorerna för transformation från målsystemet till utgångsystemet.
När parametertiden ökar flyttar jag mig i min koordinattidsriktning x2 och besättningen
flyttar sig i sin koordinattidsriktning x'2 där vinkeln mellan x2 och x'2 är α och
sin α = v där v är rymdskeppets rumshastighet. Transformationsmatrisen för kontravariant
transformation blir då
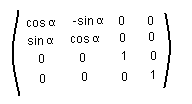 När man inte insåg skillnaden mellan parametertid och koordinattid trodde man att
transformationen måste ge oförändrad ljushastighet. En transform som uppfyller det kravet
är Lorentztransformen med transformationsmatrisen
När man inte insåg skillnaden mellan parametertid och koordinattid trodde man att
transformationen måste ge oförändrad ljushastighet. En transform som uppfyller det kravet
är Lorentztransformen med transformationsmatrisen
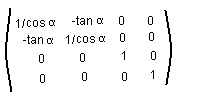 Men denna uppfyller inte ortogonalitetsvillkoret. Den transformerar alltså inte från mitt
till besättningens koordinatsystem.
Lorentztransformationen transformerar alltså inte till besättningens koordinatsystem utan
till en bild som jag gör. Det påminner om att jag ritar en perspektivbild som bara liknar
verkligheten sedd från min utgångspunkt.
När det gäller transform mellan mitt och besättningens koordinatsystem finns det två viktiga
aspekter att tänka på.
Den första är att mitt koordinatsystem beskriver en qvaolym där bara en liten del har någon
koppling till mitt medvetande. För mig finns vid en viss parametertid bara det som finns i min
egoqvaolym, i mitt påverkansnu, i mitt samtidsnu och i mitt observationsnu. Resten av världen
kan jag varken se eller påverka. Och i besättningens koordinatsystem har inte bara koordinaterna
ändrats, även påverkansnu, samtidsnu och observationsnu har ändrats. Besättningen kan alltså
se och påverka en del av världen som är oåtkomlig för mig.
Den andra aspekten är att jag måste accelerera om jag vill komma ombord på rymdskeppet.
För att komma från mitt till besättningens koordinatsystem måste jag alltså gå mot ett
gravitationsfält. Det innebär att min gravitationshöjd ökar. Ökad gravitationshöjd innebär att
ljushastigheten ökar vilket innebär ändrad skala. Man får alltså en skaländring på liknande
sätt som när man på en karta enligt Mercators projektion flyttar sig mot polen.
Men denna uppfyller inte ortogonalitetsvillkoret. Den transformerar alltså inte från mitt
till besättningens koordinatsystem.
Lorentztransformationen transformerar alltså inte till besättningens koordinatsystem utan
till en bild som jag gör. Det påminner om att jag ritar en perspektivbild som bara liknar
verkligheten sedd från min utgångspunkt.
När det gäller transform mellan mitt och besättningens koordinatsystem finns det två viktiga
aspekter att tänka på.
Den första är att mitt koordinatsystem beskriver en qvaolym där bara en liten del har någon
koppling till mitt medvetande. För mig finns vid en viss parametertid bara det som finns i min
egoqvaolym, i mitt påverkansnu, i mitt samtidsnu och i mitt observationsnu. Resten av världen
kan jag varken se eller påverka. Och i besättningens koordinatsystem har inte bara koordinaterna
ändrats, även påverkansnu, samtidsnu och observationsnu har ändrats. Besättningen kan alltså
se och påverka en del av världen som är oåtkomlig för mig.
Den andra aspekten är att jag måste accelerera om jag vill komma ombord på rymdskeppet.
För att komma från mitt till besättningens koordinatsystem måste jag alltså gå mot ett
gravitationsfält. Det innebär att min gravitationshöjd ökar. Ökad gravitationshöjd innebär att
ljushastigheten ökar vilket innebär ändrad skala. Man får alltså en skaländring på liknande
sätt som när man på en karta enligt Mercators projektion flyttar sig mot polen.