1999-12-20 - 2000-01-
Leif Andersson
Henriksbergsvägen 104
136 67 HANINGE
Tel 08/777 45 33
e-post lean@lexsup.se
Hemsida http://www.lexsup.se
FYSIK - ENLIGT MIN VÄRLDSBILD
Inledning
=========
När jag en gång i tiden började läsa fysik på gymnasiet tyckte jag att
presentationen var enkel och lättfattlig.Och jag tyckte att den gav en
god beskrivning av hur världen fungerade.Men allteftersom åren har gått
har jag stött på sådant som fått mig att ändra min världsbild och som
fått mig att undra "Varför berättade ingen det här?".
Jag tänkte därför försöka skriva om en del av gymnasiets fysik och ta med
det som jag tycker borde ha ingått.
Samma synsätt återkommer under "Vad är teknik?" men jag tror att ämnet är
tillräckligt betydelsefullt för att inte bara vara värt en mässa utan
åtminstone två.Jag har försökt att använda något olika utgångspunkter för
att kunna beskriva samma saker på något olika sätt.
Avsnitt med grön färg kräver lite mer förkunskaper.Dessa
avsnitt kan man hoppa över utan att förlora sammanhanget.
Bortom tid och rum
==================
När vi som barn blir medvetna om vår omgivning börjar vi fråga "Vad
finns bortom?" , "Vad fanns före?" och "Vad kommer efter?".Och varje
gång vi får ett svar förskjuter vi gränserna för den värld vi upplever
som känd och ställer på nytt samma frågor.
Till slut brukar vi bli avspisade med att frågorna är meningslösa och
att ingen kan svara på dem.Men så är det faktiskt inte.Vi kan faktiskt
ibland hitta absoluta gränser.Det kanske mest iögonfallande exemplet är
absoluta nollpunkten för temperatur.
När man upptäckte att gaser ökade tryck och/eller volym när man värmde
dem fick man ett sätt att mäta temperatur.Vår instinkt att fråga "Vad
finns bortom?" ledde till att man började fundera kring frågan "Hur
kallt kan det bli?".Och svaret var faktiskt inte "Hur kallt som helst".
Om man kylde en gas vid konstant tryck minskade dess volym.Men till slut
kom man till volymen noll.Och eftersom vi inte kan tänka oss vad negativ
volym skulle kunna vara insåg man att det finns en absolut nollpunkt för
temperatur.
När vi tittar på en avlägsen stjärna tittar vi inte bara långt bort,vi
tittar även bakåt i tid.Vi ser inte stjärnan sådan den ser ut nu utan sådan
den såg ut när ljuset lämnade den.Om solen plötsligt slocknade skulle vi
inte märka något förrän det gått 8 minuter.Fram till dess skulle ljus som
var på väg mot oss när den slocknade fortsätta att komma fram.Vi ser alltså
inte solen sådan den är utan solen för 8 minuter sedan.Och avlägsna stjärnor
kan vi se för miljarder år sedan.
Liksom man en gång i tiden undrade hur kallt det kunde bli kan vi fråga oss
hur långt och hur långt tillbaka vi kan se.Och även här är faktiskt inte svaret
"Hur långt som helst".
Ljus kan uppfattas som en vågrörelse och färger som frekvensen hos denna
vågrörelse.Blått ljus har hög frekvens och rött ljus har lägre frekvens.Vitt
ljus är en blandning av olika färger d v s av olika frekvenser men blandningen
är inte jämn.Frekvenserna är koncentrerade till s k spektrallinjer som motsvarar
egenskaper hos de ämnen som avgivit ljuset.Spiller man lite saltvatten i lågan
på en gasspis lyser lågan med en gul färg som motsvarar en kraftig spektral-
linje hos det natrium som ingår i saltet.
När vi tittar på ljus från fjärran stjärnor finner vi att färgen har förskjutits
mot rött.Och det är inte fråga om en omfördelning av färgintensiteter för alla
spektrallinjer har fått lägre frekvens.Det är alltså så att ljusets frekvens
blir lägre ju längre bort vi tittar.
Det innebär att om vi tittar tillräckligt långt bort blir ljusets frekvens noll.
Och liksom vi inte kan tänka oss en negativ volym kan vi inte tänka oss en
negativ frekvens.Vi kan alltså inte ha större avstånd än att ljuset som når oss
från det avståndet får frekvensen noll.Och vi kan inte ha längre tid tillbaka än
gångtiden för ljus som når oss från detta avstånd.
Hur ser då världen ut när vi kommer till största möjliga avstånd?Vi "ser" där en
värld som avger ljus med frekvensen noll d v s totalt mörker.En värld där vi inte
kan urskilja någonting.Där vi inte kan skilja två punkter från varandra och alltså
inte tala om deras läge och avstånd.En värld där vi inte kan urskilja punkter så
att vi kan säga att en händelse har inträffat genom att deras läge har förändrats.
En värld utan avstånd och utan händelser d v s en värld utan rum och tid.
Man brukar uppskatta det största möjliga avståndet till mellan 10 och 20 miljarder
ljusår och motsvarande tid blir alltså mellan 10 och 20 miljarder år.
Rum och tid är alltså ändliga begrepp som endast har mening lokalt i den värld där
vi råkar befinna oss.Utanför denna världs rum och tid råder en jämn fördelning,d v s
ett totalt mörker där allt överallt är lika.Vi kommer ur ett totalt mörker,vi går
mot ett totalt mörker och vi omges av ett totalt mörker.Men den störning av detta
perfekta tillstånd som vi kallar världen är tillräckligt stor för att vi skall
kunna ha en hel del skoj på vägen.
Tid
===
En stillastående värld är ointressant.
Det finns en gammal film,jag tror den hette "A kind of stopwatch" om en man med
ett stoppur som har den egenskapen att när han startar det stannar allt i hela
världen utom han själv.Han använder det för att plundra en bank där han i lugn
och ro kan gå omkring bland stillastående kunder och tjänstemän.Men när han skall
trycka igång världen igen tappar han uret i golvet så att det går sönder och han
blir fast i en meningslös stillastående värld.
Lyckligtvis står vår värld inte stilla.Den är stadd i ständig förändring.
För att få ett mått på världens förändring kan vi dela in den och se den som
summan av en massa små händelser.
Den minsta händelse vi kan observera innebär att någon urskiljbar punkt förändrar
sitt läge i förhållande till övriga urskiljbara punkter med den minsta detekterbara
lägesförändringen.Vi kan kalla en sådan händelse för en enhetshändelse.Så kan vi
dela in världens förändring i enhetshändelser (det blir ett stort och
ohanterligt tal men det blir ett ändligt tal).
Enligt föregående avsnitt kan vi finna en gräns för hur långt tillbaka vi kan gå
och vi kan alltså finna en siffra som anger totala antalet enhetshändelser som
inträffat i vår värld.Siffran blir stor och vi har inte mätmetoder som gör att
vi kan bestämma den särskilt noggrant men vi kan konstatera att denna siffra finns
och vi kan kalla den för "absolut tid".
Vi kan uppskatta den absoluta tiden till att nu vara c:a 15 10120 enhetshändelser.
Det finns en mängd olika uppskattningar av Hubble-konstanten men låt oss anta att
universums ålder är 15 miljarder år och radien 15 miljarder ljusår.Medeltätheten
kan uppskattas till 4 10-26 kg/m3.Vilket innebär att totala innehållet
är 2 1053 kg eller 2 1070 J.Om vi dividerar med Plancks konstant får
vi motsvarande frekvens som alltså blir 3 10103 Hz.Inverterar vi det värdet får vi
periodtiden som vi kan använda som mått på kortast möjliga tid d v s som mått på
den tid som åtgår för en enhetshändelse.Vi får alltså fram att det går 3 10103
enhetshändelser på en sekund och att en enhetshändelse tar 3 10-104 s.Då 15 miljarder
år är 5 1017 s innebär det att den absoluta tiden nu är c:a
15 10120 enhetshändelser
Men även om vi inte kan bestämma den absoluta tiden särskilt noggrant och även om
den absoluta tiden blir ohanterligt stor kan vi,med stor noggrannhet,mäta tiden
mellan två händelser som inträffar inom vårt observationsområde.
Av alla händelser som inträffar i universum är de allra flesta helt slumpmässiga.
Det är bara en mycket liten del som vi kan påverka.Men enhetshändelser har en
tendens att bilda mönster och samordnas till större händelser som vi kan
observera.Eftersom sådana inträffar helt slumpmässigt kan vi utgå från att om
vi nöjer oss med att observera en viss typ av händelse inom ett litet område så
får vi ett mått på totala antalet händelser.Vi kan t ex bygga ett pendelur och
räkna med att varje gång händelsen att pendeln fullbordat ett slag har inträffat
har det gått en sekund d v s har det inträffat 3 10103 enhetshändelser i hela
universum.Att den andel av det totala antalet händelser som vi mäter på detta sätt
är konstant kan vi övertyga oss om genom att göra två likadana klockor och se
om de går likadant.Vi finner då att om vi kan isolera dem från störande
inverkan utifrån går de nästan exakt lika.Mer om tekniken att mäta tid hittar
du under "Vad är teknik" på denna sida.
Rum
===
På liknande sätt som vi kan definiera en enhetshändelse kan vi definiera en
enhetslängd.En enhetslängd är helt enkelt den sträcka ljuset hinner gå under en
enhetshändelse.
Vårt universum blir då ett rum i form av ett klot med radien 15 10120 enhetslängder.
Detta klot kan vi dela in i enhetsceller med en enhetslängd som sidlängd.Detta
klot rymmer alltså c:a 1 10364 enhetsceller.
Om vi även vill räkna in alla enhetsceller som någonsin funnits får vi betrakta
tid som en fjärde dimension.Vi får då ett fyrdimensionellt halvklot med c:a
1 10485 enhetsceller.
En enhetscell ligger på gränsen till att vara observerbar.Det går alltså inte att
urskilja några detaljer i den.Vi kan bara skilja mellan om den innehåller något eller
om den är tom.Vi kan alltså fullständigt beskriva den med en etta eller en nolla.
Världen är alltså ett "datorminne" som rymmer 1 10364 bits och som totalt
har hanterat 1 10485 bits.
Med "avstånd" mellan A och B menar vi det antal enhetsceller vi måste passera för att
komma från A till B.
Vi kan alltså se på världen som en dator med ett enormt minne.Men en dator är
praktiskt taget oanvändbar om den inte har ett operativsystem som gör att innehållet
i minnet ändras enligt vissa regler.Och även världen har sitt "operativsystem".Hur
detta fungerar är vad fysik egentligen handlar om.
Orsak och verkan
================
För att bli användbar behöver en dator något operativsystem med någon form av BIOS
(Basic In/Out System).Ännu mer fundamentalt är att man redan i processorns hårdvara
brukar lägga in vissa begränsningar av hur minnet kan förändras.Man brukar t ex
dela in minnet i grupper om 8 , 16 eller 32 bits som hanteras samtidigt.
För att kunna använda datorn måste vi komma fram till en förenklad uppfattning av
den,en uppfattning som är användbar och som kan rymmas inom vår tankeförmåga.Vi
börjar då med att bortse från ettor och nollor för att i stället se grupper av
bits som vi kallar bytes.
På liknande sätt finner vi att världen har ett "BIOS" som grupperar enhetsceller.
Sammanhängande grupper av enhetsceller kallar vi partiklar och vi finner att det
finns förvånansvärt stabila sådana.Av någon,för oss okänd,anledning förblir
mönstret av ettor och nollor inom en partikel ofta konstant även om partikeln
ändrar läge i förhållande till andra partiklar.
Även i tidsled grupperar världens "BIOS" enhetshändelser till händelsekedjor som
bildar urskiljbara mönster.Om vi vet vad som har hänt kan vi,i vissa fall,förutse
vad som kommer att hända.Om vi vet att en partikel har förflyttat sig i ett område
med enbart nollor kan vi förutse att den kommer att fortsätta förflyttningen.
Vi kallar den förflyttning som redan skett för orsak och den som vi förutser för
verkan.
Vi har funnit ett antal orsak-verkan-samband som vi kan använda som ett sorts
högnivåspråk för programering av världen.Om vi önskar en viss verkan men finner
att den är svår att uppnå kan vi leta bland dessa samband för att se om vi i
stället kan finna en orsak som är lätt att åstadkomma och som ger önskad verkan.
Eller en orsak som har en verkan som kan vara orsak till den önskade verkan.Eller
en orsak till en orsak till en orsak till verkan.
Människor har naturligtvis alltid använt sig av orsakskedjor för att nå sina mål.
Men till en början skedde detta huvudsakligen intuitivt.Att orsaka en spräckning
av ett flintstycke så att man får en användbar flintkniv är en konst som våra
förfäder utvecklade och förfinade.Man lärde sig orsakskedjorna men man
verbaliserade dem inte.Lärlingen lärde sig huvudsakligen genom att se och höra
mästarens slag och genom att själv slå med slagsten på flinta.
Kring mitten av det gångna årtusendet började en målmetveten strävan att
verbalisera orsak-verkan-samband.Detta lyckades över förväntan och så sent som
under adertonhundratalets slut trodde man på fullt allvar att varje verkan
kunde knytas till orsaker som i sin tur kunde knytas till orsaker.
Kvantfysiken och speciellt Heisenbergs osäkerhetsrelation bröt med denna
föreställning genom att hävda att ett orsak-verkan-samband säger att en orsak
innebär en viss sannolikhet för en viss verkan.Denna sannolikhet kan vara nära
ett men den är alltid mindre än ett.
Om man släpper en sten är sannolikheten stor att den faller nedåt.Men det finns
en liten,beräkningsbar,sannolikhet att den faller uppåt.Denna sannolikhet är
naturligtvis så liten att vi,för praktiskt bruk,kan strunta i den.Men att den
finns är principiellt viktigt för det innebär att världen kan komma med
överraskningar.
Heisenbergs osäkerhetsrelation bygger på insikten att världen både har partikel-
karaktär och vågkaraktär samtidigt.Men en våg måste observeras under åtminstone
större delen av periodtiden innan man kan veta att det verkligen rör sig om en
våg.En ansamling fyllda enhetsceller,d v s en ansamling ettor,kan bilda en
partikel.Ju fler ettor den innehåller ju högre säger vi att dess energi är.
Och när vi använder vågbeskrivning blir dess frekvens energin dividerad med
Plancks konstant.Ju högre energi den har ju högre frekvens och därmed kortare
periodtid har den.
Något förenklat kan man säga att Heisenberg påpekade att man måste observera
en energimängd under dess periodtid innan man säkert vet om den finns.
Om man vill veta hur stor en energimängd är och när den har denna storlek måste
man göra en nogrann mätning under kort tid.Men ju noggrannare man vill veta
hur stor den är ju längre tid tar mätningen.Och ju mer exakt man vill veta
mättidpunkten ju sämre hinner man mäta energiinnehållet.
Heisenberg konstaterade att om man samtidigt försöker mäta två storheter A och B
som har egenskapen att deras produkt har sorten Js så blir minsta möjliga fel
dA dB = h
där h = Plancks konstant.
Energi
======
Enhetshändelser inträffar och bildar mönster i form av händelsekedjor.Sådana
händelsekedjor kallar vi händelser.Händelser inträffar hela tiden.Dessa
händelser är helt enkelt tiden.
Av alla händelser som inträffar är det en mycket liten del som vi kan
förutse och påverka.Men hur liten den delen än är är den viktig för oss.Så
viktig att vi behöver ett särskilt begrepp för den.Vi kallar förutsebara,
påverkbara händelser för energi.
Det förefaller som om vi inte kan tömma eller fylla en enstaka enhetscell.
Vi kan alltså inte göra om en etta till en nolla eller tvärtom.Däremot kan
ettor byta plats med nollor.Så vitt vi vet består alla händelser vi observerar
i att ettor och nollor byter plats.Världens BIOS tycks se till att minnet hela
tiden har lika många ettor.
Nollor är mycket vanligare än ettor i vår värld.Om vi påträffar en fylld
enhetscell,d v s en etta,kan vi alltså förutse att den kommer att bytas ut mot
en nolla.De ettor vi observerar är alltså förutsägbara förändringar d v s
förutsägbara och därmed påverkbara händelser,d v s energi.
Den tätaste materia vi känner är den som finns i kollapsade stjärnor.Om vi
antar att denna materia består av enbart ettor kan vi uppskatta andelen ettor
i vår del av världen.Jag har inte kunnat finna någon bra uppgift om tätheten
för denna typ av materia men om man räknar om "populära" uppgifter som vad en
apelsin skulle väga o dyl kommer man till c:a 3 1010 kg/m3.
Medeltätheten i vår del av världen rör sig om 4 10-26 kg/m3.
Förhållandet mellan dessa tätheter utgör ett mått på andelen ettor i vår värld.
Det går alltså c:a 1036 nollor på varje etta.
Även i den tätaste materia vi känner här på jorden går det mer än en miljon
nollor på varje etta.
En enhetshändelse innebär alltså att en etta och en nolla byter plats.Eftersom
antalet ettor är så mycket mindre än antalet nollor är det antalet ettor som
anger hur ofta detta sker.Antalet ettor inom en viss volym anger alltså hur
många förutsebara händelser som kommer att inträffa i volymen d v s hur stor
energi som finns i volymen.
Om man kan avgränsa en viss volym så att den inte kan utbyta ettor mot nollor
eller tvärsom över volymgränsen blir antalet ettor d v s energin konstant inom
volymen.
Detta brukar kallas för termodynamikens första huvudsats och formuleras som att
energin hos ett slutet system är alltid konstant.
Men en enhetshändelse är mycket liten,så liten att vi inte känner något sätt att
utnyttja en enstaka enhetshändelse.Att försöka finna en enstaka etta för att
kunna utnyttja att vi kan förutse att den kommer att bytas ut mot en nolla är
som att försöka manipulera gener med grävskopa.Våra sinnen,instrument och verktyg
är trubbiga och vi behöver enhetshändelser som sker samordnat till användbara
händelser.Om vi avgränsar en viss volym så att den bildar ett slutet system
kan det hända att fördelningen av ettor inom systemet är ojämn.Vi kan t ex
ha många fler ettor i ett hörn än i resten av volymen.Vi kan då,inte bara förutse
att varje etta kommer att bytas mot en nolla,vi kan förutse att sådana byten
kommer att ske oftare i detta hörn än i resten av volymen.Och detta kan ske i
en skala som vi kan använda.En sned fördelning av ettor inom ett slutet
system kan vi alltså använda.Men det är användbart därför att vi kan förutse
att fördelningen kommer att utjämnas och när vi använder det utjämnas för-
delningen och blir oanvändbar.
Detta brukar kallas för termodynamikens andra huvudsats.Den formulerades i en
tid när man främst var intresserad av att omvandla värme till arbete och när man
fann att man måste ha en sned temperaturfördelning för att omvandla värme till
arbete.Den brukar därför formuleras:Entropin (värmelärans motsvarighet till
ellärans laddning eller mekanikens tyngd) hos ett slutet system kan inte
minska.
(Lite mer om entropibegreppet finns i en gammal artikel som jag tyvärr bara
har kvar på engelska.Klicka på Entropy så kommer du till den
artikeln.)
En konsekvens av andra huvudsatsen är att tiden bara går åt ett håll.I stället
för att säga "Entropin hos ett slutet system kan inte minska" skulle vi kunna
säga "Tiden kan inte minska".
När vi var små spelade min bror och jag ibland schack.Det hände att vi hamnade
i lägen där vi inte kunde komma på vad vi skulle göra härnäst.Jag kunde då
flytta tornet ett steg för att i nästa drag återgå till utgångsläget och han
kunde göra likadant.Så kunde vi "spela" hur länge som helst utan att ställningen
förändrades.Spelet gick bara framåt av irreversibla drag t ex flyttning av en
bonde,att någon slog en pjäs eller att någon gjorde ett drag som öppnade nya
möjligheter.
Om en etta byter plats med en nolla går tiden fram en enhet.Men om nästa
enhetshändelse är att ettan återgår till utgångsläget går tiden bakåt en
enhet.Ingen kan veta att något har hänt.Alla minnen består av enhetsceller
och för att någon skall kunna minnas en händelse måste den orsaka en
händelsekedja som ställer om något minne.
Liksom schackspelet går tiden bara framåt av händelser som är eller som på
grund av andra händelser blir irreversibla.
När man började studera möjligheter att omvandla värme till arbete fann man
att man vanligen utgick från värme med hög temperatur och liten entropi för
att sluta med en rest av värme vid omgivningstemperatur med högre entropi
än utgångsvärmet.Entropiökningen innebar att man inte,genom att omvandla det
utvunna arbetet tillbaka till värme,kunde komma tillbaka till utgångsläget.
Man började därför betrakta entropi som ett mått på irreversibilitet.Och
begreppet används idag i vidgad betydelse så att man t ex vid kemiska
reaktioner talar om en entropiterm som anger reaktionens grad av
irreversibilitet även om det inte direkt är fråga om en omvandling till
värme.
Med denna vidgning av begreppet blir alltså entropiökning en synonym till
tidökning.Och andra huvudsatsen utsäger det vi alla av erfarenhet vet,
nämligen att tiden bara går åt ett håll.
Termodynamikens första och andra huvudsatser är viktiga regler som vi kan
använda när vi försöker utnyttjas världens BIOS.Men utöver dem finns det andra
hinder för utjämning mellan ettor och nollor.Möjligheten att avgränsa slutna
system innebär att det finns möjligheter att "låsa in" ettor i avgränsade
volymer där utjämning med omgivningen inte sker trots att den borde göra det
enligt första och andra huvudsatsen.Vi har t ex inte funnit något sätt
att få materia att restlöst omvandla sig till andra energiformer trots
att första och andra huvudsatsen säger att det borde vara möjligt.
Arbete
======
Antag att jag skall lyfta en säck mjöl.
Jag skall då genomföra den procedur som inom datatekniken kallas för shift.
Via världens BIOS anropar jag shift-proceduren för alla de bits som utgör
säcken.Detta anrop omfattar en lång och komplicerad händelsekedja men på
samma sätt som en dators operativsystem gömmer programelement för operatören
är denna kedja okänd för mig.Jag vet bara att jag anropar shift-proceduren
genom att ta tag i säcken och lyfta.
När alla de bits som utgör säcken skiftats mot ovanförliggande bits har säcken
lyfts en enhetslängd och det är bara att anropa shift-proceduren på nytt och
på nytt tills jag fått upp den tillräckligt.
Jag finner nu att det krävs en viss viljeansträngning för att jag,på detta
sätt,skall anropa shift-proceduren.Utförande av något som kräver viljeansträng-
ning kallar vi arbete.Här på jorden är det tydligen så att det krävs arbete
för att lyfta föremål.Att lyfta är en typ av förflyttning och jag finner att
även andra typer av föremålsförflyttning kan kräva arbete.Inom fysik gör man
den förenklingen att man enbart talar om sådant arbete som är knutet till
förflyttning av föremål.
Om jag provar att lyfta olika säckar till olika höjd finner jag att det krävs
mer arbete att lyfta en säck ju högre jag lyfter den och det krävs mer arbete
ju mer det är i den.Åker jag till månen finner jag också att det krävs mer
arbete att lyfta en viss säck till en viss höjd på jorden än på månen.
Shift-proceduren innebär ju en förutsägbar och avsiktlig förändring.Den är
alltså energi.Arbete i fysikalisk mening är alltså en form av energi.Men även
om det krävs lika mycket energi,d v s arbete,för att lyfta en lätt säck till
hög höjd som att lyfta en tung säck till låg höjd är dessa procedurer olika
och vi behöver metoder att beskriva dem som visar hur de skiljer sig från
varandra.
Vi gör då en uppdelning i
Antal ettor som skall skiftas
En faktor som anger hur svårt det är att skifta på den plats man är
Antal shift-procedurer som krävs
Vi säger att
W = mg h
där
W = det arbete,d v s den energi,som krävs för lyftet (Work)
m = säckens massa d v s antalet ettor som ingår i säcken
g = gravitationskonstanten som är olika på jorden och på månen
h = lyfthöjden,d v s antal erforderliga shift-procedurer
Produkten mg kallar vi säckens tyngd.
Vi delar alltså upp energin i två faktorer där den ena (tyngden) anger hur stor
mängd vi arbetar med.Vi kallar denna faktor för extensiv faktor eller mängdfaktor.
Den andra faktorn anger hur stor förändring varje del av mängden utsätts för.Vi
kallar den faktorn för intensiv faktor.
För min mjölsäck är alltså tyngden (mg) extensiv faktor och lyfthöjden (h)
intensiv faktor.
Kraft
=====
Vi säger att mjölsäckens tyngd är en kraft.För att åstadkomma denna anropar
jag shift-proceduren via världens BIOS.Men jag finner att jag behöver göra
likadana anrop i en rad andra fall.Om jag skall dra ett föremål över ett
strävt underlag,om jag skall sätta fart på en sten för att kasta den,om
jag skall dra en båt i vatten måste jag göra likadana proceduranrop.Vi
kallar alla sådana anrop för kraft oavsett om vi åstadkommer dem själva
eller om vi utnyttjar någon maskin för att göra dem.
Att anbringa en kraft på ett föremål är en uppmaning till föremålet att
förflytta sig.Om det förflyttar sig sker en förändring d v s energi omsätts.
Kraften gånger förflyttningslängden är den omsatta energin.
För att kunna räkna med krafter behöver vi något hanterligt mått på dem.
Vi använder oss då av den regel i världens BIOS som säger att om ingenting
bromsar rörelsen kommer en kraft som verkar på en massa att öka dess hastighet.
Vi kallar den kraft som varje sekund ökar hastigheten hos en massa på 1 kg med
1 m/s för 1 N (Newton).Vi har alltså att
1 N = 1 kg m/s2
Vi använder oss av krafter för att åstadkomma önskade förändringar där och när
vi vill ha dem.Men förändringar inträffar också hela tiden spontant.Om vi vill
åka med ett luftskepp från Stockholm till Göteborg startar vi en drivmotor som
ger en kraft som förflyttar skeppet mot Göteborg.Denna kraft gånger den väg vi
färdas är det arbete,d v s den energi,som vi måste tillföra.Men det är viktigt
att observera att denna energitillförsel inte är nödvändig för att vi skall
komma till Göteborg i och för sig.Den är nödvändig för att vi skall kunna
förutsäga när vi kommer till Göteborg.Om vi lät skeppet driva omkring i luft-
havet i oändlig tid skulle vi naturligtvis,förr eller senare,hamna över
Göteborg och då skulle vi alltså ha fullbordat resan.Men det är ett mycket
opraktiskt sätt att resa.Vi behöver åtminstone någon typ av kraft som gör att
vi kan förutsäga färdvägen lite bättre.
Den fyrdimensionella världen
============================
Med avståndet mellan punkterna A och B menar vi det minsta antal enhetsceller
man måste passera för att komma från A till B.På liknande sätt kan man
definiera tidsavståndet mellan händelserna a och b som det antal enhetshändelser
som inträffar mellan a och b.
Ett sätt att hantera avstånd mellan ett stort antal punkter är att lägga in dem
i ett treaxligt koordinatsystem.I stället för att ange alla möjliga avstånd kan
vi då ange alla punkters koordinater och ur dessa beräkna de avstånd vi vill
veta.
Det ligger nära till hands att lägga till en koordinataxel och använda den för
att ange tidskoordinat.Med avstånd i ett sådant fyraxligt koordinatsystem menar
vi då,inte bara antal enhetsceller mellan A och B utan också antal enhetshändelser
mellan att vi utgår från A och kommer fram till B.
Om vi använder ett sådant fyraxligt koordinatsystem kan vi ge tid två olika
betydelser.Vi kan dels tala om tid som en förändringsparameter.Vi kan kalla
detta för parametertid.Och vi kan tala om tid som en lägeskoordinat i vår
fyrdimensionella värld.
Så kan vi naturligtvis göra men normalt växer parametertiden och koordinattiden
likadant.Finns det då någon anledning att skilja på begreppen?Finns det något
i världens BIOS som går att beskriva genom att vi skiljer på begreppen?
Världens BIOS uppför sig faktiskt som om det fanns något som strömmade med viss
hastighet åt något håll i den fyrdimensionella rymden.Vi har inget bra namn på
detta något.Det har kallats världseter eller Brahma men låt oss för enkelhets
skull kalla det för eter.
Om allt står stilla i rummet strömmar etern i tidsriktning.Och hastigheten blir
c = t/tp
där
c = eterns strömningshastighet d v s ljushastigheten
t = koordinattid
tp = parametertid
Allt står då stilla i rummet och följer med en eter som strömmar i tidsled.
Om något rör sig i rummet kan vi uppfatta detta som att hastigheten där ändrar
riktning.Om något föremål flyttar sig sträckan s på parametertiden tp säger vi
att det rör sig med hastigheten v enligt
v = s/tp = c sin(a)
där
a = vridningsvinkeln för föremålets hastighetsvektor
Man kan uppfatta ljus som en ström av partiklar,fotoner,som rör sig med ljus-
hastighet i rummet.Fotonernas hastighetsvektor har alltså vridits 90 grader så
att de rör sig i rummet men står stilla i tiden.
Om man,likt Munchhausen,kunde hoppa ombord på en foton och titta bakåt skulle
man se startplatsen sådan den såg ut när man startade.Alla klockor på startplatsen
skulle då stå stilla.Man skulle inte röra sig i startplatsens tidsled.Men man
skulle röra sig med ljushastighet i någon annan riktning som man själv skulle
uppfatta som tidsriktningen och de som var kvar på startplatsen skulle kalla en
rumsriktning.
Gravitation
===========
Betrakta två partiklar A och B på avståndet ab.
I fig 1 anger den blå ytan alla punkter som ligger närmare A än vad B gör.Och
den gula ytan anger punkter som ligger längre ifrån A än vad B gör.Om nu B
rör sig helt slumpmässigt i förhållande till A finns det uppenbarligen många
fler punkter dit B kan gå för att öka avståndet till A än punkter dit B kan
gå för att minska avståndet.
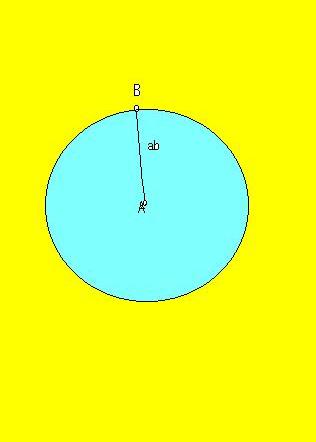Fig 1
Sannolikheten att avståndet ökar är alltså större än sannolikheten att det
minskar.Partiklarna kommer alltså att uppföra sig som om de stötte bort varandra.
Vi kan uppfatta detta som en utåtriktad gravitation.
Vi har alla sett att ljuset bryts vid en vattenyta eller vid en glasyta i t ex
en lins.Detta kan förklaras med att ljushastigheten är lägre i vatten och glas
än den är i luft.Det förefaller alltså som om ljushastigheten c är lägre i
områden med större antal ettor.Om vi använder bilden av en eter som strömmar i
tidsled i en fyrdimensionell rymd skulle detta innebära att etern släpar efter
i områden med förhållandevis många ettor.En stor massa innebär alltså en
etereftersläpning som medför att runt massan kröks eterns strömningsriktning
inåt mot massan.Eterns strömningsriktning får alltså här en komposant i
rumsriktning.En partikel som svävar fritt i etern kommer alltså att dras in
mot massan.
Michelson-Morleys spegelförsök visade att jorden inte rör sig i förhållande
till en omgivande eter.
Eftersom föremål kan röra sig i förhållande till varandra ansåg man att de
inte alla kunde vara i vila i förhållande till omgivande eter.Man tolkade
därför försöket som att det inte kan finnas någon eter.
I ett medium som i det närmaste är inkompressibelt,som vatten,gäller att mediets
strömningsriktning blir praktiskt taget densamma i närliggande punkter.Men redan
med den kompressibilitet som luft har kan man ha närliggande vindbyar med
olika riktning.
Ombord på en ballong blåser det aldrig trots att man kan ha betydande hastighet
i förhållande till andra ballonger inom synhåll.Luftens kompressibilitet gör att
ballonger som alla befinner sig i vila i förhållande till omgivande luft ändå
kan röra sig i förhållande till varandra.
Och varför skulle etern vara inkompressibel?
Är inte föreställningen att jorden faktiskt befinner sig i vila i förhållande till
omgivande eter på samma sätt som en ballong är i vila i förhållande till omgivande
luft en mer näraliggande tolkning av Michelson-Morleys spegelförsök?
Runt massor får vi alltså en "etervind" in mot dem.Om man befinner sig tillräckligt
nära en tillräckligt stor massa kommer denna etervind att dominera över den
utåtriktade gravitationen och vi får en inåtriktad gravitation.
Gravitation är alltså utåtriktad men lokalt kring en massa inåtriktad.
Liv
===
Till en dator skaffar vi ett antal program som,med hjälp av datorns operativsystem,
åstadkommer spektakulära effekter.Till världsdatorn har bl a uppstått ett program
som vi kallar "Liv".
Liksom vi till datorn använder disketter och CD-rom för att lagra program använder
liv DNA för lagring av programet.
Vi har nyligen upptäckt hur denna lagring går till och vi är nu i full gång med
att skapa en debugger som fått namnet HUGO.
Med HUGO öppnar vi programet liv för läsning i assemblerspråk.Vi får allt i form
av anrop till världens BIOS men fortfarande har vi långt kvar innan vi kan tolka
vad vi får fram.Alla som försökt dekompilera ett program vet hur svårt det är att
hålla reda på vad instruktionerna innebär.Eftersom en dator blandar instruktioner
och data i samma minne brukar man snart blanda ihop data med instruktioner
och gå vilse i programet.Och när det gäller världens BIOS vet vi inte ens hur
data och instruktioner hålls isär.Och redan nu visar HUGO en mängd programtext
som vi inte vet om den har någon funktion.Är det bara rester av gammal fel-
programering?Är det element som haft en funktion men som senare ersatts av andra
element?Eller är det livsviktiga instruktioner?
Olika energiformer
==================
Enhetshändelser inträffar ständigt men med våra trubbiga sinnen och instrument kan
vi inte utnyttja enstaka enhetshändelser.Vi är hänvisade till att arbeta med
händelsekedjor som ger så stora förändringar att vi kan uppfatta dem.I stället
för att arbeta med enstaka enhetsceller och enhetshändelser arbetar vi med
medelvärde,varians och rumshastighet.
Våra sinnen är programerade för att anropa världens BIOS via några olika typer
av anrop och vi tolkar detta som att vi har tillgång till olika energiformer.
Men även om vi upplever att det är skillnad mellan t ex elektrisk energi och
värme behandlar vi alla energiformer enligt samma regler.
Oavsett vilken energiform det är fråga om betraktar vi energi som en produkt
av en mängd (extensiv faktor) och en intensitet (intensiv faktor).
Mängden kan bero på hur vi avgränsar det system vi betraktar.Om vi har en hink
med varmt vatten så har vi värme i den.Om vi häller upp halva hinken i en skål
får vi halva värmeenergin i skålen men det betyder inte att värme omvandlats
till någon annan energiform bara att vi avgränsat mängden på ett nytt sätt.
Om däremot den intensiva faktorn ändras kan,men behöver inte,energi omvandlas
till annan energiform.Om vi låter vattnet i hinken driva en värmemaskin omvandlas
en del värme till arbete och intensiteten,d v s temperaturen hos vattnet,sjunker.
Om den intensiva faktorn ändras från T1 till T2 kan alltså energi
omvandlas till annan energiform t ex till utvinnbart arbete.Det arbete som går att
få ut från en sådan omvandling för mängden S är
W = S (T1 - T2)
Läran om energiomvandling har utvecklats vid olika tidpunkt för olika energiformer.
Resultatet har blivit att man valt begrepp,sorter och mätmetoder på något olika
sätt så att det inte alltid är uppenbart att det grundläggandet resonemanget är
identiskt.Det krävs alltså lite tankearbete för att se vad som motsvarar vad men
det lönar sig att inse att t ex elektrisk intensitet är arbete per laddningsenhet
(V = J/As),potentiell intensitet är arbete per tyngdenhet (höjd i m är J/tyngd i N),
värmeintensitet (=temperatur) är arbete per entropienhet (K = J/(J/K)),intensitet för
pneumatisk energi (=volym) är arbete per tryckenhet (m3 = J/Pa),intensitet för
rörelseenergi (=hastighet) är arbete per rörelsemängd (=impuls) o s v.
Genom att på detta sätt se hur man organiserat tänkandet slipper man läsa statik,
dynamik,ellära,värmelära,pneumatik,fysikalisk kemi mm som av varandra oberoende
läror.Man kan identifiera det som är gemensamt och bara slå i sig det lilla som
blir kvar som unikt för varje energiform t ex vad begreppen har för namn.
Mängdändring
============
Man kan,som sagt,inte omvandla energi bara genom att ändra gränserna för den
energimängd man betraktar.Men det förekommer att mängd faktiskt skapas eller
förintas vilket medför energiomvandling.
Uppdelningen i extensiv mängdfaktor som inte ger energiomvandling vid förändring
och intensiv faktor som är lika för alla delar av mängden och som ger energi-
omvandling vid förändring är alltså inte så självklar som det kan förefalla vid
första påseendet.
För pneumatisk energi är tryck extensiv och volym intensiv faktor.Man kan se det
som att trycket åstadkoms genom att man tillför luftmängd och varje delmängd som
man tillför fyller ut hela volymen så att alla delmängderna har samma volym d v s
samma intensitet.Men det känns ändå lite besynnerligt att inte betrakta volym som
en mängdstorhet.Och om man minskar volymen på en sluten behållare så ökar trycket,
extensiv och intensiv faktor är då kopplade till varandra så att båda ändras.
Hur hanterar man fall där mängden inte är konstant?
Betrakta en vattenfylld bassäng med vertikala väggar.Den energi som vi kan ta ut
om vi tömmer bassängen är vattnets tyngd gånger dess fallhöjd.
Om vattenytan är A och bassängens höjd h blir vattnets tyngd
På liknande sätt gäller för rörelseenergi att rörelsemängden d v s impulsen mv
varierar med intesiteten d v s med hastigheten v.Och även här får vi ett liknande
uttryck för uttagbar energi.Den blir
W = m v2/2
Om sorter
=========
Påståendet att 15 äpplen är 1 glas mjölk och 3 ostbitar är uppenbart nonsens.
Man kan inte lägga ihop mjölk och ost och än mindre få äpplen som resultat.
I exemplet ovan kan vi kalla 15 , 1 och 3 för mätetal och "äpplen" , "glas
mjölk" och "ostbitar" för sorter.Vanligtvis behöver vi hantera storheter av
varje sort för sig.Vi kan t ex säga att 10 äpplen plus 5 äpplen är 15 äpplen.
Alla termer skall alltså ha samma sort.
När man börjar läsa fysik är denna regel ett mycket användbart hjälpmedel för
att kontrollera beräkningar.När man ställer upp olika samband lär man sig att
alltid göra en sortkontroll d v s att se efter vilken sort de ingående termerna
har.Skulle någon term ha en annan sort än de övriga tyder det på att man gjort
något fel.Om man försöker lägga ihop längd mätt i meter med tid mätt i sekunder
har man troligen gjort något fel.
Våra måttsystem har utvecklats ur ungefärliga begrepp som volymen "tunna råg",
tiden "en halvdag",temperaturen "byxljummen" o s v.Men ökad köpenskap och ökad
rörlighet ställde krav på exaktare mätningar.Handlaren som köpte råg i tunnor
och sålde i påsar behövde veta hur många påsar det gick på en tunna.Och den
som skulle köra och hämta någon från tåget behövde veta när tåget skulle
komma.
Man började fundera på hur och vad vi kunde mäta.Till en början var det t ex
inte alls självklart att en fast mängd kunde mätas upp med samma typ av
volymmätning som användes för vätskor.Gjorde man en flätad måttkorg för att
mäta upp råg kunde den inte användas för vatten.Och om man sög upp vatten i
en mätkammare kunde man inte använda samma utrustning för att mäta upp råg.
Men så småningom enades vi om att sådana problem är av praktisk natur och
att de inte motsäger det principiella påståendet att det går att åstadkomma
volymmått som är användbara för såväl råg som vatten.Vi kunde göra oss av
med ett antal gamla mått och i stället mäta alla volymer i samma mått.
Så började man fundera på hur många olika sorter man behövde utgå ifrån för
att få fram alla sorter som man behövde i det dagliga livet.Om man hade bestämt
sig för en längd som fick utgöra längdenhet kunde man göra en kvadrat med denna
längdenhet som sida.Därigenom fick man en ytenhet utan att man behövde bestämma
sig för någon ny grundstorhet.Och man kunde åstadkomma en volymenhet genom att
göra en kub med längdenheten som sida.
Man kom till att man behövde enheter för längd,massa och tid för att kunna
härleda praktiskt taget alla de sorter man behövde.Vi fick cgs-systemet med
centimeter för längd,gram för massa och sekund för tid.
Om man skall kasta en sten gäller att kraften som man kastar med blir massan
gånger accelerationen.Hastighet är förflyttning per sekund och har alltså sorten
cm/s.Accelerationen är hastighetsändring per sekund och får alltså sorten cm/s2.
Massan mäts i gram och sorten för kraft blir alltså g cm/s2.Denna sort kan man
använda för alla krafter oavsett om de sätter fart på en kaststen eller lyfter
mjölsäckar.
En nackdel med cgs-systemet var att det inte gav en enhetlig behandling av
elektriska storheter.Man kunde dels utgå från elektrostatisk kraftverkan mellan
laddade partiklar dels från magnetisk kraftverkan mellan elektriskt laddade
partiklar i rörelse.Resultatet blev två måttsystem ese (elektrostatiska enheter)
och eme (elektromagnetiska enheter).Dessutom fick man ofta räkna med obekvämt
många nollor för storheter av alldaglig storhet.
Resultatet blev att man övergick till MKSA-systemet baserat på meter,kilogram,
sekund och ampere.Genom att lägga till ampere fick man en enhetlig behandling
av elektriska storheter.
Under en tid användes även det s k tekniska systemet som inte hade massa utan
kraft som en grundenhet.I stället för kilogram använde man tyngden av ett
kilogram som grundenhet.Men resultatet blev att många fick svårt att skilja
mellan massa och kraft.Fortfarande ser man manometrar graderade i kg/cm2 när
man naturligtvis menar kp/cm2 där kp (kilopond) är tyngden (=den kraft
som jordens dragningskraft ger) av ett kg.
Efter vissa justeringar blev MKSA-systemet internationell standard och döptes
om till SI-systemet.
Multiplicera en tid som har sorten s med en hastighet som har sorten m/s så får
resultatet sorten s m/s. Förkorta med s så ser man att resultatet får sorten m
vilket innebär att det är en längd.Tid gånger hastighet ger alltså längd.Vet man
hur lång tid en bil kör och med vilken hastighet den går kan man alltså räkna ut
hur långt den kommer.
Multiplicerar man en tid (s) med en kraft (kg m/s2) och dividerar med en massa
(kg) får resultatet sorten m/s.Resultatet blir alltså en hastighet.Om man vet hur
stor massa den sten man kastar har,hur lång tid kastet tar och vilken kraft man
kastar med kan man alltså räkna ut stenens utgångshastighet.
Ett sätt att lösa gymnasietidens övningsuppgifter och skrivningar var,åtminstone på
min gymnasietid,att se efter
Vilka storheter är givna och vad har de för sorter
Vilka storheter efterfrågas och vad har de för sorter
Hur kan man kombinera givna storheter så att resultatet får efterfrågad sort
Det är naturligtvis inte alltid självklart vilken hastighet som hör ihop med vilken
tid och vilken massa som påverkas av vilken kraft men metoden brukade räcka för att
ge godkänt även om man inte hade någon aning om vad man gjorde.
Metoden gav god utdelning för minimalt arbete och efteråt har jag förstått att jag
faktiskt lärde mig mer än de som mödosamt pluggade in alla formler och regler.
Måttsystem
==========
Om man vill mäta längden på en sträcka kan man lägga ena tummen vid ändpunkten.Så
lägger man den andra tummen intill,"vandrar" med tummarna bort till andra ändpunkten
och räknar antalet tumbredder.Är det fråga om en lite längre sträcka kan man sätta
hälen vid ena ändpunkten,"vandra" tå mot häl till andra ändpunkten och räkna antalet
fotlängder.
Detta är ett praktiskt sätt som vi nog har medfött.Och för sortomvandlingen mellan
tum och fot använde man sig av att det går 12 tum på en fot.Tolv är ett utmärkt
sortomvandlingstal som är jämnt delbart med 2,3,4 och 6.
För volym och vikt utgick man från vad man kunde lyfta,hur mycket man kunde dricka
o dyl.Tid angav man ofta i den tid som åtgick för någon vardaglig händelse o s v.
Detta var praktiskt men inexakt.Människor hade olika breda tummar och olika långa
fötter.Med franska revolutionen kom en ny syn på mått och vikt.Man släppte kravet
på anknytning till dagligt bruk och satte sig vid skrivbordet för att konstruera
"rationella" mått.
Vid skrivbordet föreföll tio vara bättre än tolv för omräkning mellan olika mått
av samma slag.Man skapade därför ett system med tiopotens-multiplar för att
åstadkomma hanterliga mått.Vårt talsystem har tio som bas därför att vi räknat
på våra tio fingrar (utom danskarna som även räknat på tårna).Men tio är bara
jämnt delbart med 2 och 5 vilket bl a ger problem med den,i praktiken ofta
förekommande,divisionen med 3.
Så skulle man överge tum som längdmått och i stället välja en längdenhet som alla
hade tillgång till och som var exakt lika lång för alla.Vid skrivbordet kan man
se jorden som tillgänglig för alla.Man utgick därför från jordens omkrets.Men det
blev en så opraktiskt stor enhet att man t o m vid skrivbordet insåg att man
måste välja en mindre del.Man delade därför in omkretsen i fyra kvadranter och
definierade längdenheten meter som en tiomiljontedel av en sådan kvadrant d v s
som en fyrtiomiljontedel av jordens omkrets.
Det låg också något av en tanke i att använda jordrotationen för att definiera en
tidsenhet d v s att låta sekund vara en viss del av dygnet och att använda jordens
omkrets för att fastställa en längdenhet.På det viset knöt man både längd och
tid till jordklotet.
Nu hade man fått en exakt och för alla lika längdenhet.Nu var det bara att sätta
igång och tillverka meterstavar för praktiska mätningar.Man skickade ut lantmätare
för att mäta upp jordens omkrets och fastställa meterns längd.De mätte men
det där med exakthet var inte så enkelt i verkligheten.När man hade prånglat ut
alltför många meterstavar för att kunna ta tillbaks dem började man förstå att
mätningarna var så felgjorda att man inte kunde behålla den ursprungliga
definitionen.
Det stolta meterprojektet,skrivbordsförnuftets triumf över vardagen,flaggskeppet i
krämarnas uppror mot adeln,hade havererat.
Nu gällde det att rädda ansiktet.Man gjorde en arkivmeter (antagligen tog man
helt enkelt någon prototyp till meterstav) som stämde väl med de meterstavar
man prånglat ut och förkunnade att en meter var arkivmeterns längd.Och man
vände sig till Napoleon.Han förfogade över argument av annat slag och kunde
sprida metersystemet utan några besvärande frågor om varför arkivmetern hade
just den längden.England och USA,som inte kom under Napoleons välde,behöll
tumsystemet långt in på 1900-talet.
Som enhet för massa tänkte man sig att använda gram definierat som massan hos
en kubikcentimeter vatten.Men även här övergick man till att knyta definitionen
till en arkivenhet.
Det här med arkivmeter och arkivkilogram fungerade hjälpligt men det smakade lite
nederlag om det.Krämarna hade inte lyckats lyfta sig över sin praktiska användning
av mätstickor och vikter för att skapa ett måttsystem som förankrats i något högre
än vardagens triviala utminutering av handelsbodens produkter.
Men om vi kunde finna någon universell,överallt och för alla lika hastighet skulle
vi kunna koppla längd och tid till varandra.Vi skulle kunna multiplicera tidsenheten
med denna hastighet och få en längd som vi kunde använda för att definiera en
längdenhet.
Ljushastigheten är en sådan universell hastighet och idag knyter vi tidsenheten till
periodtiden och längdenheten till våglängden för en viss spektrallinje hos cesium.
På liknande sätt kan vi,med hjälp av Plancks konstant,knyta enheten för massa till
enheterna för längd och tid.
Och som framgår ovan är det möjligt att definiera en absolut tid i en,av våra
måttsystem oberoende,absolut enhet.För närvarande är våra möjligheter att mäta
denna enhet så dåliga att vi inte utnyttjar denna möjlighet.Vi vill inte göra
om fadäsen med mätningen av jordens omkrets.Men vi vet idag att det är möjligt
att skapa ett måttsystem som är helt fritt från godtyckliga arkivmått.
__________________________________
-------------------------
Till http://www.lexsup.se