2000-01-12
Leif Andersson
Henriksbergsvägen 104
136 67 HANINGE
Tel 08/777 45 33
e-post leif.andersson@haninge.mail.telia.com
Hemsidor http://go.to/lean1
http://come.to/lean
Etervind
========
Antag att en observatör står på jorden och betraktar en förbiflygande raket.
Ombord på raketen finns också en observatör.Såväl jordobservatören (J) som
raketobservatören (R) finner att de rör sig med hastigheten c i tidens
riktning.Deras koordinattid (t) växer alltså när parametertiden (τ) ökar.
Om de mäter såväl koordinattid som parametertid i sekunder blir hastigheten
c = t/τ = 1 s/s
och om de mäter koordinattid i meter och parametertid i sekunder blir
hastigheten
c = t/τ = 3 108 m/s
Såväl J som R upplever också att de,förutom tidsriktningen,även omges av ett
rum med tre ortogonala riktningar.De befinner sig alltså i en fyrdimensionell
rymd.Det är emellertid svårt att rita upp ett fyrdimensionellt koordinatsystem
så man kan göra den förenklingen att man antar att allt av intresse som händer
i rummet sker i x-led.Man behöver då enbart en rumsaxel för att beskriva rummet.
J och R befinner sig då i var sitt koordinatsystem med axlarna t och x där
t-axeln är koordinattid och x-axeln är rumsaxel.
J och R upplever att de befinner sig i likadana koordinatsystem men eftersom
raketen rör sig i förhållande till jorden är deras koordinatsystem vridna i
förhållande till varandra.Kalla vridningsvinkeln för α.
Vi har alltså den situation som framgår av fig 1.
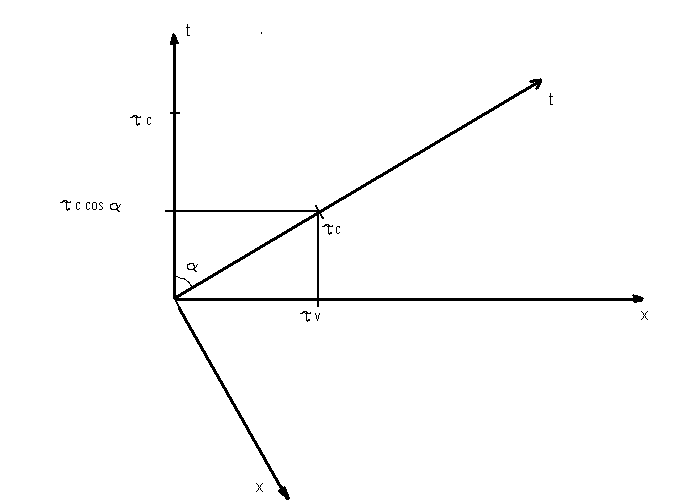fig 1
På parametertiden τ rör sig J τc i tidsled d v s längs sin tidsaxel.
På samma sätt gäller för R att han ökar sin koordinattid med τc på
parametertiden τ.Båda står stilla i sina koordinatsystem vilket innebär
att x förblir noll för båda.
Men när J ser på R för att få reda på hur hans tid och rumsläge förändras
projicerar J R:s koordinattidsförändring på sina egna koordinataxlar.J säger
då att R har förflyttat sig τc cos α i tidsled och τc sin α i x-led.
Med raketens hastighet menar J raketens förflyttning i x-led på en tidsenhet av
parametertiden.Hastigheten v blir alltså
v = τc sin α /τ = c sin α
Och raketens hastighet i J:s koordinattid blir inte c som den är för J utan i
stället c cos α.Genom att raketen har en hastighet i J:s rum följer den inte
riktigt med i J:s tid.Tidseftersläpningen blir
c - c cos α = c (1 - cos α)
Vi kan kalla
(1 - cos α)
för tidens eftersläpningsfaktor.
För små värden på α kan vi sätta
sin α = α
och
cos α = 1 - α2/2
Vi får då
v = c α
som ger
α = v/c
och
cos α = 1 - (v/c)2/2
Tidens eftersläpningsfaktor blir alltså
(1 - cos α ) = ( 1 - (1 - (v/c)2/2)) = (v/c)2/2
Om vi väljer att mäta t och τ i samma enhet blir c = 1 och tidens
eftersläpningsfaktor blir
v2/2
d v s rörelseenergin per massenhet.
J säger alltså att raketens hastighet är sinus för koordinatsystemens vridnings-
vinkel och att raketens rörelseenergi är raketmassan gånger tidens eftersläpnings-
faktor d v s raketmassan gånger ett minus cosinus för koordinatsystemens vridnings-
vinkel.
Vi kan se det som att J och R båda flyter med,som ballonger,i en eter som strömmar
med hastigheten c i koordinattidens riktning.Eller också kan vi vända på det och
säga att både J och R väljer att göra sina koordinatsystem så att koordinattidsaxeln
sammanfaller med eterns strömningsriktning.Därigenom ser de det som att de ligger
stilla i rummet och att det enbart är tiden som ändras.
Men eterns strömningsriktning är olika för J och R.Deras koordinatsystem blir vridna
i förhållande till varandra.När de ser på varandras c-vektor finner J att R:s
hastighet inte är en ren tidshastighet utan att den har en komposant även i rummet.
Denna komposant kallar han för R:s hastighet.På motsvarande sätt ser R att J:s
c-vektor har en rumskomposant som han kallar J:s hastighet.
Vi kan alltså betrakta etern som ett strömningsfält där etern strömmar med
hastigheten c.
Vid behandlig av strömningsfält,t ex vätskeströmning,vind,värmeutbredning och
elektronflöden brukar man definiera en hastighetspotential u sådan att grad u
blir strömningshastigheten.För etern har vi då
c = grad u
där c är en vektor.
"Etervinden" blåser åt olika håll för J och R.När de lägger sina tidsaxlar i
vindriktningen finner de att de bildar vinkel med varandra.
Om eterflödet är källfritt och om etern är inkompressibel kan man inte ha olika
vindriktning.Om etervinden från alla håll blåser in mot en punkt måste etern ha
någon sänka att gå till eller kunna komprimeras i punkten.
Det är naturligtvis ingenting som hindrar att eterflödet har källor och sänkor
och att etern är kompressibel men det finns en möjlighet som nog borde undersökas
närmare.
Det kan vara så att eterflödet är källfritt i rum-tid d v s i fyra dimensioner
men har källor och sänkor i rummet d v s i tre dimensioner.
Vi skulle då ha
div4 c = 0
men kunna ha
div3 c ≠ 0
vilket innebär att
div3 = - δct/δt
I ett strömmande medium kan det förekomma virvlar.Man definierar då en virvelvektor
ω = ½ rot c
Områden där ω ≠ 0 kan uppdelas i virveltrådar eller,som det också kallas,
virvelrör.
I en uppåtströmmande värmd luftmassa kan det bildas en rak virveltråd som kallas
tromb.När man blåser ut rök kan det i den strömmande luften bildas en sluten
virveltråd där röken roterar och bildar en rökring.
För inkompressibla medier och tredimensionell strömning kan man visa att virvel-
trådar är mycket stabila företeelser.
Det är tänkbart att man kan uppfatta det vi vanligen kallar partiklar som virvel-
trådar med virvelvektorn i koordinattidens riktning.Jag vet inte om detta leder
till någon motsägelse men det kan vara intressant att undersöka detta.
___________________________________
-----------------------
Åter till hemsidan