DISKUSSIONSUTKAST
2000-01-25
Leif Andersson
Henriksbergsvägen 104
136 67 HANINGE
Tel 08/777 45 33
e-post leif.andersson@haninge.mail.telia.com
Hemsidor http://go.to/lean1
http://come.to/lean
För att de specialtecken som förekommer i artikeln skall visas korrekt krävs
Alleuropeiskt textvisningsstöd och Uniscribe. (På IE5 Visa-Kodning-Mer)
Lorentz-tranform och Minkowski-rum eller koordinatsystemvridning?
=================================================================
Tid i rummet
------------
För en varelse som endast kan se världen projicerad på en tvådimensionell yta
måste en planskiljd korsning framstå som något mycket egendomligt.Han ser bilar
köra in och komma ut utan att de påverkar varandra trots att de samtidigt
befinner sig på samma plats. Och ibland försvinner bilar när de passerar
korsningen för att strax därpå dyka upp utan att de har påverkats under passagen.
Vi har mycket gemensamt med en sådan varelse.Vi tittar på tvådimensionella bilder
i TV och tycker att de ger en god bild av verkligheten.Men vi är ändå medvetna om
att det finns en dimension till och,i viss mån,kan vi hantera tre dimensioner i
rummet.
För drygt hundra år sedan började man se att tre rumsdimensioner inte var
tillräckligt.Liksom vår tvådimensionella varelse kan förundras över att bilar
kan köra igenom den planskiljda korsningen utan att krocka borde vi förundras
över att bilar kan köra igenom en plankorsning utan att krocka.Om de kör vid
olika tidpunkt händer ingenting.Skillnad i tid fungerar här tydligen på samma
sätt som skillnad i höjd.Tydligen har tiden egenskaper som vi brukar förknippa
med rummet.
Man började fundera på vad som händer om två observatörer rör sig i förhållande
till varandra och observerar varandra.Om A rör sig i förhållande till B vad ser
då A när han tittar på B?Ser han samma bild som B ser av föremål kring B?
Man fann att man nog borde betrakta tid som en sorts fjärde rumsdimension.Tiden
hade en del egenskaper som stämde med andra rumsdimensioner men den hade också
egenskaper som inte övriga rumsdimensioner hade.
I rummet kunde man lägga in ett koordinatsystem med tre vinkelräta räta linjer
som axlar.Ett sådant system kallas cartesianskt.Att axlarna är vinkelräta innebär
att förflyttning parallellt med en axel bara påverkar en koordinat.Kallar man
axlarna x , y och z och flyttar en punkt parallellt med z-axeln förändras enbart
z-koordinaten.x- och y-koordinaterna förblir oförändrade.Vi säger att systemet är
ortogonalt.
Men hur skulle man lägga in en fjärde axel?Och hur skulle man kunna markera att
tiden som skulle ligga efter fjärde axeln var lite förmer än de andra koordinaterna?
Hermann Minkowski kom med ett förslag som var så elegant att det accepterades även
när man måste ta till skohorn för att få ner verkligheten i det.Men vad gör man
inte för att få gå i snygga skor.
Innan vi går närmare in på Minkowski-rummet lite om imaginära tal.
Imaginära tal
-------------
Man kan ordna alla tal i en följd längs en tallinje.Om man går med jämna steg längs
linjen ökar talen för varje steg med steglängden. Men om man vänder och går bakåt
minskar talen för varje steg med steglängden.Att vända är tydligen detsamma som att
multiplicera steglängden med -1.
Multiplikation med -1 betyder alltså vridning av gångriktningen med ett halvt varv
d v s 180 grader.Multiplicerar man en gång till med -1 vrider man ytterligare ett
halvt varv.Man har då vridit ett helt varv och kommit tillbaka till ursprungsriktningen.
Tydligen betyder (-1)n en vridning med n halva varv.
Men vad betyder det om vi sätter n = 1/2?
Om n anger antalet halva varv borde ju n = 1/2 betyda ett halvt halvt varv d v s
vridning 90 grader.Vi borde komma till en axel som är i rät vinkel mot tallinjen.
Efter den kan vi ordna tal på samma sätt som efter vår första tallinje och eftersom
den är vinkelrät har den ingen projektion på den första tallinjen.Om vi går
parallellt med denna nya axel ändras alltså inte läget efter första tallinjen.
Men (-1)1/2 = √-1 och något sådant tal finns inte. Enbart vid 0 har axlarna en
gemensam punkt.Vi har alltså skapat en axel som vi kan definiera matematiskt och
vi kallar den för den imaginära axeln.Men den har ingen självklar fysikalisk
innebörd.Vad vi väljer att låta den representera är helt upp till vårt godtycke.
Så varför inte använda den som en tidsaxel?
Minkowski-rum
-------------
Minkowski föreslog att man skulle sluta arbeta med rum och tid som skiljda begrepp
och i stället använda en rum-tid med fyra dimensioner där man lade in tid som en
imaginär axel.
När man inom ellära sysslar med växelström har man stor nytta av en uppdelning på
två vinkelräta axlar när man skall hålla reda på fasläge.För detta fungerar en
uppdelning i reella och imaginära tal alldeles utmärkt.En imaginär axel blir ett
hjälpmedel för att hantera tidsberoende förlopp.
Det fanns alltså en del funderingar kring användning av komplexa tal (tal med både
reell och imaginär del) för att representera tidsförlopp när Minkowski lade fram
sitt förslag om rum-tiden.
Inom matematik brukar man beteckna √-1 med i.Inom ellära är detta opraktiskt
eftersom man där använder i som strömsymbol och man brukar därför använda
beteckningen j för √-1.Jag kommer här att använda i.
För att beräkna avståndet mellan två punkter i ett rätlinjigt ortogonalt
koordinatsystem kan man lägga ihop kvadraterna på avståndets projektion på
axlarna och dra roten ur summan.Om axelprojektionerna av avståndet ds är
dx , dy , dz blir
ds2 = dx2 + dy2 + dz2
Om vi nu skall betrakta även tiden som en rumskoordinat får vi lägga till
tidsprojektionen också.Detta ger
ds2 = dx2 + dy2 + dz2 + dt2
Punkter i Minkowski-rummet kallas för händelser.
I Minkowski-rummet avsätts inte tid som en lägeskoordinat vilken som helst utan
en sorts "den tid man har på sig".Om vi avsätter ct efter tidsaxeln för att få den
graderad i samma enheter som rumsaxlarna d v s i m betyder alltså punkt A i fig 3
en händelse som ligger ctA m i tidsled från startpunkten.
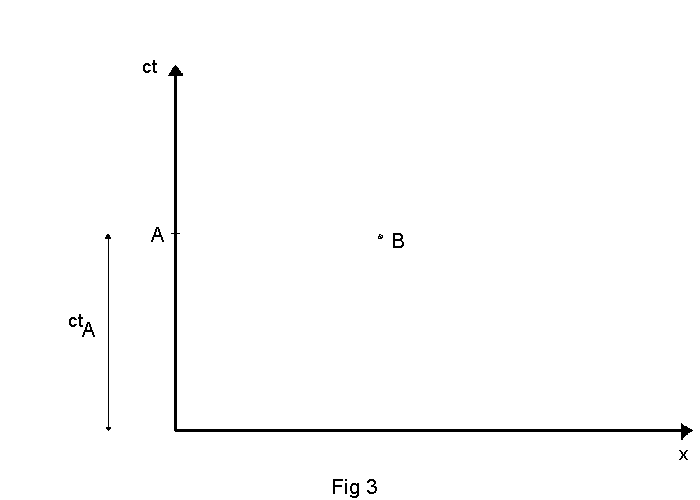 B är en händelse som ligger vid
xB + i ctB
Beloppet av detta komplexa tal är B:s avstånd från origo men om vi tar realdelen
i kvadrat och imaginärdelen,inklusive i,i kvadrat får vi en sorts avstånd s enligt
sB2 = xB2 - (ctB)2
Enligt vårt vanliga vardagsspråk inträffar B vid starttiden d v s vid ct = 0.Men
eftersom den inträffar på avståndet xB når inte någon information om den
fram till tidsaxeln förrän ct = xB.
Om vi tar med i i dt i uttrycket för ds ovan blir alltså inte ds ett avstånd i vanlig
mening utan ett sorts "samtidighetsmått".
Om
xB = ctB = ctA
når informationen från B fram till tidsaxeln just när A inträffar.En observatör i
punkten A säger alltså att händelserna A och B är "samtidiga".
När Ptolemaios skulle beskriva stjärnors rörelser utgick han från sfäriska skal
som roterade runt jorden.Det var en elegant modell.Så elegant att hans världsbild
stod sig i många århundraden trots att den var mycket svårhanterlig.
Minkowski-rummet är elegant men för att tillämpa det på verkligheten får vi ta
till skohorn för att tolka begrepp som avstånd,samtidighet och tidsökning.Lite
sakadar det de fina skorna men liksom Ptolemaios fick sin stjärnkarta att
stämma fick Minkowski sin rum-tid att stämma.
Lorentz-transformen
-------------------
Om en skytt står på marken och avlossar ett gevär får kulan en utgångshastighet
som vi kan kalla vg.Oavsett vilken riktning han skjuter i får kulan
samma hastighet i förhållande till jorden.
Så sätter vi honom på ett lastbilsflak och sätter fart på bilen.Om bilen har
hastigheten vb gäller att om han skjuter framåt får kulan
utgångshastigheten i förhållande till jorden vg + vb och om han skjuter
bakåt blir utgångshastigheten i förhållande till jorden vg - vb.
Skjuter han åt sidan blir hastigheten i sidled vg.Han får då också en
hastighetskomposant i bilens körriktning.
Om ljus beter sig som gevärskulan skulle en observatör på marken som mäter
ljushastighet finna att om man ställer en strålkastare på bilflaket och mäter
hastigheten hos det ljus som kommer från den får man c + vb om
man mäter framför bilen i en framåtriktad stråle, c - vb om man
mäter bakom bilen i en bakåtriktad stråle och c om man mäter hastighet i
sidled.Strålen i sidled skulle emellertid inte gå rakt ut utan snett framåt.
Men så är det inte!Alla mätningar av ljushastigheten ger värdet c.
Det skulle kunna bero på att hastigheten alltid är konstant i förhållande
till ett ljusbärande medium på samma sätt som ljudhastigheten alltid är
konstant i förhållande till luften oberoende av hur ljudkällorna rör sig.
Om det är så kan vi göra en anordning enl fig 1 och prova att vrida den i
olika riktningar för att se om det blir någon skillnad på gångtiderna.
B är en händelse som ligger vid
xB + i ctB
Beloppet av detta komplexa tal är B:s avstånd från origo men om vi tar realdelen
i kvadrat och imaginärdelen,inklusive i,i kvadrat får vi en sorts avstånd s enligt
sB2 = xB2 - (ctB)2
Enligt vårt vanliga vardagsspråk inträffar B vid starttiden d v s vid ct = 0.Men
eftersom den inträffar på avståndet xB når inte någon information om den
fram till tidsaxeln förrän ct = xB.
Om vi tar med i i dt i uttrycket för ds ovan blir alltså inte ds ett avstånd i vanlig
mening utan ett sorts "samtidighetsmått".
Om
xB = ctB = ctA
når informationen från B fram till tidsaxeln just när A inträffar.En observatör i
punkten A säger alltså att händelserna A och B är "samtidiga".
När Ptolemaios skulle beskriva stjärnors rörelser utgick han från sfäriska skal
som roterade runt jorden.Det var en elegant modell.Så elegant att hans världsbild
stod sig i många århundraden trots att den var mycket svårhanterlig.
Minkowski-rummet är elegant men för att tillämpa det på verkligheten får vi ta
till skohorn för att tolka begrepp som avstånd,samtidighet och tidsökning.Lite
sakadar det de fina skorna men liksom Ptolemaios fick sin stjärnkarta att
stämma fick Minkowski sin rum-tid att stämma.
Lorentz-transformen
-------------------
Om en skytt står på marken och avlossar ett gevär får kulan en utgångshastighet
som vi kan kalla vg.Oavsett vilken riktning han skjuter i får kulan
samma hastighet i förhållande till jorden.
Så sätter vi honom på ett lastbilsflak och sätter fart på bilen.Om bilen har
hastigheten vb gäller att om han skjuter framåt får kulan
utgångshastigheten i förhållande till jorden vg + vb och om han skjuter
bakåt blir utgångshastigheten i förhållande till jorden vg - vb.
Skjuter han åt sidan blir hastigheten i sidled vg.Han får då också en
hastighetskomposant i bilens körriktning.
Om ljus beter sig som gevärskulan skulle en observatör på marken som mäter
ljushastighet finna att om man ställer en strålkastare på bilflaket och mäter
hastigheten hos det ljus som kommer från den får man c + vb om
man mäter framför bilen i en framåtriktad stråle, c - vb om man
mäter bakom bilen i en bakåtriktad stråle och c om man mäter hastighet i
sidled.Strålen i sidled skulle emellertid inte gå rakt ut utan snett framåt.
Men så är det inte!Alla mätningar av ljushastigheten ger värdet c.
Det skulle kunna bero på att hastigheten alltid är konstant i förhållande
till ett ljusbärande medium på samma sätt som ljudhastigheten alltid är
konstant i förhållande till luften oberoende av hur ljudkällorna rör sig.
Om det är så kan vi göra en anordning enl fig 1 och prova att vrida den i
olika riktningar för att se om det blir någon skillnad på gångtiderna.
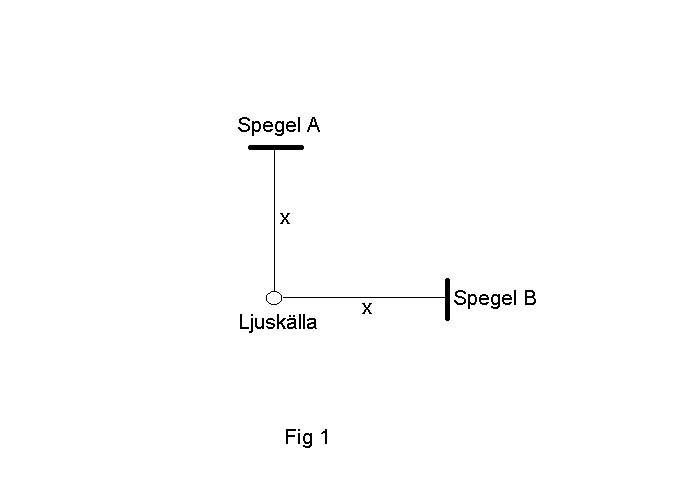 Om vi rör oss med hastigheten v så att spegel A ligger rakt framåt följer vi
med ljuset när det går fram i den ljusbärande etern. Ljushastigheten i
förhållande till vår anordning blir då c - v och gångtiden fram till
spegel A blir x/(c - v).Så vänder ljuset och går mot anordningens
färdriktning.Ljushastigheten i förhållande till anordningen blir
då c + v och gångtiden tillbaka från spegel A blir x/(c + v).
Om vi rör oss med hastigheten v så att spegel A ligger rakt framåt följer vi
med ljuset när det går fram i den ljusbärande etern. Ljushastigheten i
förhållande till vår anordning blir då c - v och gångtiden fram till
spegel A blir x/(c - v).Så vänder ljuset och går mot anordningens
färdriktning.Ljushastigheten i förhållande till anordningen blir
då c + v och gångtiden tillbaka från spegel A blir x/(c + v).
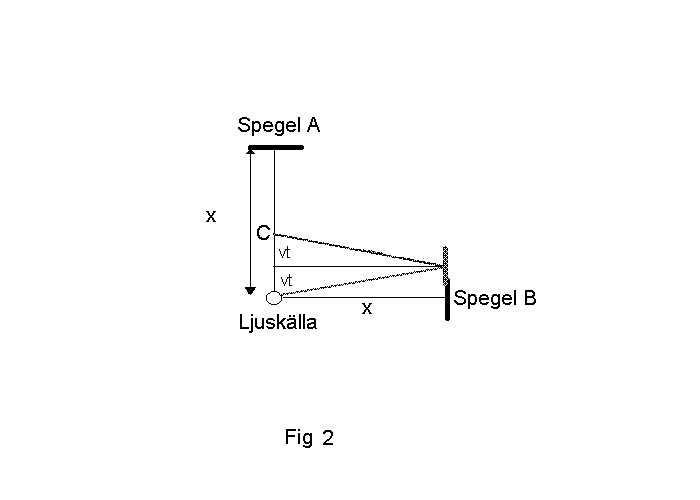 I sidled går strålen snett framåt.Den går till spegel B och reflekteras så att den
återkommer när ljukällan är vid C.Om vi kallar gångtiden fram till spegel B för
t hinner spegeln gå sträckan vt innan ljuset kommer fram till den.Gångvägen blir då
sB = √(x2 + (vt)2)
och gångtiden blir
sB
t = --
c
Detta ger
(tc)2 = x2 + (vt)2
t2 (c2 - v2) = x2
x
t = ---------
c √(1 - (v/c)2)
Ljuset kommer alltså tillbaka från spegel A efter tiden
x x 2 c x 2 x 1
tA = ----- + ------ = ------- = ---- -------
c-v c+v c2 - v2 c 1 - v2/c2
och ljuset kommer tillbaka från spegel B efter tiden
2 x 2 x 1
tB = 2 t = --------------- = --- ------------- = tA √(1 - (v/c)2)
c √(1 - (v/c)2) c √(1 - (v/c)2)
tA är alltså större än tB.Hastigheten c-v ger ökad gångtid som inte helt
kompenseras av att c+v ger minskad gångtid.Och den förlusten blir större än den
förlust som den ökade gångvägen i sidled ger.
Man förlorar mer på en hastighetsminskning än man vinner på en lika stor
hastighetsökning.Antag att en person har 3 mil till jobbet och brukar köra med 90
km/tim.Det tar då 20 min d v s 40 minuter restid per dag.Om han en dag kör
80 km/tim på ditvägen tar det 22,5 minuter.Om han försöker kompensera det
genom att köra 100 km/tim på hemresan tar den 18 minuter.Hans sammanlagda
restid blir då 40,5 minuter d v s en halv minut längre än normalt.Tydligast
kan man se detta om man tänker sig att han minskar hastigheten på ditvägen
med 90 km/tim d v s går ner till hastigheten noll.Då kommer han fram först
efter oändlig tid och det kan han inte kompensera genom att köra 180 km/tim
på hemresan.
Men när Michelson och Morley försökte mäta skillnaden på gångtid i olika riktningar
fann de att den alltid var noll.Ljus beter sig tydligen varken som gevärskulor eller
ljud.
Låt oss då se lite närmare på situationen att vi har en observatör med mätanordningen
på ett bilflak och en observatör på marken.Observatören på bilflaket säger: "Jag är
världens medelpunkt.Jag står stilla.Det är klart att jag mäter samma gångtid för
ljus i alla riktningar.Att marken under bilen rör sig har ingenting med mina
mätningar att göra."
Observatören på marken säger:"Gångtiden i sidled måste ha blivit längre eftersom
ljuset nu får gå längre väg och gångtiden fram och tillbaka till spegel A måste ha
blivit ännu längre.Hur kan flakobservatören,t ex via en mobiltelefon,påstå att
gångtiderna är lika?"
När markobservatören och flakobservatören skall beskriva världen omkring sig
kan de göra upp var sitt koordinatsystem.Dessa gör de naturligtvis så att de
själva är stilla i dem.Bådas system ser likadana ut men båda ser att den andres
system rör sig med hastigheten v.Frågan är då:"Hur överför vi koordinater från
det ena systemet till det andra?"
Vi kan kalla markobservatörens koordinatsystem xj där j inte är en exponent
utan ett superscript som anger nummer på koordinataxeln.Om han gör ett fyraxligt
system med tre rumsaxlar och en tidsaxel går alltså j från 1 till 4.På samma
sätt kallar vi flakobservatörens koordinatsystem xj.
Om de lägger origo i samma punkt och vrider axlarna lika gäller att systemen
sammanfaller när bilen står stilla.Om en vektor har axelprojektionerna
Aj j = 1 till 4
i markobservatörens system gäller då för axelprojektionerna i flakobservatörens
system att
Aj = Aj j = 1 till 4
vi kan skriva
4
Aj = ∑ Ajk Ak = Ajk Ak
k=1
(Om tensorkalkyl se min tekniksida Tekniksida (http://w1.877.telia.com/~u87701228))
Vi kan skriva Ajk som en transformationsmatris
1 0 0 0
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Denna överför axelprojektionerna av vektorn A oförändrade till axelprojektionerna
av vektorn A.
Om axel nr 1 är x-axeln och axel nr 4 är tidsaxel så borde det förhållandet att bilen
sätter fart och kör med hastigheten v i x-riktningen bara betyda att flakobservatörens
avstånd från punkter i x-led minskar med v gånger tid.Det innebär att Ajk blir
1 0 0 -v
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Detta var den typ av koordinattransformation som Gallilei och Newton använde.Men
den gav olika resultat när markobservatören och flakobservatören skulle tala om
vad som hände när flakobservatören använde instrumentet enl fig 1.Den stämde inte
heller med Maxwells ekvationer.
1903 föreslog Hendrik Antoon Lorentz att man skulle använda en transformationsmatris
enligt
γ 0 0 -γv/c
0 1 0 0
Ajk =
0 0 1 0
-γv/c 0 0 γ
där
γ = 1/√(1 - (v/c)2)
Och ser man på.Nu stämde det.Einstein fortsatte med att popularisera resultatet.
Vad som händer är att när markobservatören försöker se på flakobservatörens klocka
så finner han att den går för sakta.Och när flakobservatören håller upp en meterstav
i färdriktningen så finner markobservatören att den är kortare än en meter.
När markobservatören ser på strålen till spegel B säger han att gångtiden har ökat
för att strålen går längre väg.Men flakobservatören ser ingen förlängning av vägen
och ingen förlängning av gångtiden men nu kan markobservatören förklara det med att
flakobservatörens klocka går saktare.
Det samma gäller strålen till spegel A men här har dessutom avståndet till spegeln
minskat.När markobservatören ser på anordningen finner han att spegel A har kommit
närmare ljuskällan.Att flakobservatören mäter oförändrad gångtid till spegel A
beror alltså,enligt markobservatören,dels på att hans klocka går saktare dels på att
spegel A kommit närmare.
(Hoppas jag har vänt allt rätt och fått allt på rätt plats.Det är mycket att
hålla reda på och sånt är inte min starka sida.Tala om om du hittar något fel.)
Koordinattid
------------
Hittills har jag bara beskrivit det synsätt som idag är vedertaget.
När Gallilei,Kopernicus och Kepler flyttade världens centrum till solen blev
stjärnkartan mycket enklare.Det betydde inte att den heliocentriska världsbilden
i någon absolut mening var mer rätt än Ptolemaios.Och fortfarande är Ptolemaios
karta,på sätt och vis,elegantare eftersom den arbetar med cirklar som bl a Platon
ansåg vara fulländade figurer.Men den heliocentriska världsbilden blev så enkel
att vi idag kan lära ut den redan till barn på lågstadiet.
Trots att det gått c:a 100 år sedan Minkowski-rummet och Lorentz-transformen
presenterades lär vi inte ut detta på lågstadiet.Minkowskis rum-tid kräver en
viss vana vid att hantera komplexa tal och,även om några tillämpningar av
Lorentz-kontraktionen blivit allmängods,kräver Lorentz-transformatinen en viss
vana vid tensorkalkyl.
Kan vi,som Gallilei gjorde,flytta observationspunkten och få en enklare bild?
En rymdresenär som färdas bort från jorden i en riktning som vi kan kalla
x-riktningen ser hela tiden ett växande avstånd till jorden.För honom blir
x-riktningen en tidsaxel.I stället för att mäta tid med klocka kan han mäta
tid med avståndet till jorden.
Tiden har egenskaper som sammanfaller med rumskoordinater och rumskoordinater
har egenskaper som sammanfaller med tid.
Vad händer om vi säger att det förutom de vanliga tre rumsaxlarna finns en
fjärde axel som är vinkelrät mot de övriga?Vi kan inte rita ett sådant system
och vi kan inte få in alla fyra axlarna i det tredimensionella rummet men det
behöver ju inte betyda att det inte finns en sådan axel.
Om det finns en sådan axel kan vi avsätta tid efter den och kalla den för
koordinattid.De egenskaper hos tiden som inte är av koordinatkaraktär kan vi
samla i ett nytt tidsbegrepp som vi kan kalla parametertid.
Så kan vi säga att alla dessa fyra axlar har identiska egenskaper.Vi kan vrida
systemet hur vi vill och låta koordinattidsaxeln bli en rumsaxel eller låta
en rumsaxel byta plats med koordinattiden.Hur vi än flyttar och vrider
koordinatsystemet skall alla fysikaliska lagar fortsätta att gälla.Världen
kan inte veta hur vi lägger in koordinatsystem.Den beter sig likadant oavsett
hur vi ändrar koordinatsystemet.
Så antar vi att vi alla färdas med ljushastighet c i någon riktning i detta
fyraxliga koordinatsystem.
Om vi ligger stilla i rummet d v s om x- , y- och z-koordinaterna är oförändrade
betyder det att vi har lagt koordinattidsaxeln i vår färdriktning.Vi rör oss
då med ljushastighet i tidsriktningen och ligger stilla i rummet.
Det som händer när vi rör oss med hastigheten v i rummet är inte,som i Minkowski-
rummet,att vi lägger till en hastighet utan att vi vrider vår hastighetsriktning.
Vi rör oss fortfarande med ljushastighet men inte längre rakt i tidsriktningen.
Vi har vridit hastigheten så att vi fått en hastighetskomposant i rummet.
I sidled går strålen snett framåt.Den går till spegel B och reflekteras så att den
återkommer när ljukällan är vid C.Om vi kallar gångtiden fram till spegel B för
t hinner spegeln gå sträckan vt innan ljuset kommer fram till den.Gångvägen blir då
sB = √(x2 + (vt)2)
och gångtiden blir
sB
t = --
c
Detta ger
(tc)2 = x2 + (vt)2
t2 (c2 - v2) = x2
x
t = ---------
c √(1 - (v/c)2)
Ljuset kommer alltså tillbaka från spegel A efter tiden
x x 2 c x 2 x 1
tA = ----- + ------ = ------- = ---- -------
c-v c+v c2 - v2 c 1 - v2/c2
och ljuset kommer tillbaka från spegel B efter tiden
2 x 2 x 1
tB = 2 t = --------------- = --- ------------- = tA √(1 - (v/c)2)
c √(1 - (v/c)2) c √(1 - (v/c)2)
tA är alltså större än tB.Hastigheten c-v ger ökad gångtid som inte helt
kompenseras av att c+v ger minskad gångtid.Och den förlusten blir större än den
förlust som den ökade gångvägen i sidled ger.
Man förlorar mer på en hastighetsminskning än man vinner på en lika stor
hastighetsökning.Antag att en person har 3 mil till jobbet och brukar köra med 90
km/tim.Det tar då 20 min d v s 40 minuter restid per dag.Om han en dag kör
80 km/tim på ditvägen tar det 22,5 minuter.Om han försöker kompensera det
genom att köra 100 km/tim på hemresan tar den 18 minuter.Hans sammanlagda
restid blir då 40,5 minuter d v s en halv minut längre än normalt.Tydligast
kan man se detta om man tänker sig att han minskar hastigheten på ditvägen
med 90 km/tim d v s går ner till hastigheten noll.Då kommer han fram först
efter oändlig tid och det kan han inte kompensera genom att köra 180 km/tim
på hemresan.
Men när Michelson och Morley försökte mäta skillnaden på gångtid i olika riktningar
fann de att den alltid var noll.Ljus beter sig tydligen varken som gevärskulor eller
ljud.
Låt oss då se lite närmare på situationen att vi har en observatör med mätanordningen
på ett bilflak och en observatör på marken.Observatören på bilflaket säger: "Jag är
världens medelpunkt.Jag står stilla.Det är klart att jag mäter samma gångtid för
ljus i alla riktningar.Att marken under bilen rör sig har ingenting med mina
mätningar att göra."
Observatören på marken säger:"Gångtiden i sidled måste ha blivit längre eftersom
ljuset nu får gå längre väg och gångtiden fram och tillbaka till spegel A måste ha
blivit ännu längre.Hur kan flakobservatören,t ex via en mobiltelefon,påstå att
gångtiderna är lika?"
När markobservatören och flakobservatören skall beskriva världen omkring sig
kan de göra upp var sitt koordinatsystem.Dessa gör de naturligtvis så att de
själva är stilla i dem.Bådas system ser likadana ut men båda ser att den andres
system rör sig med hastigheten v.Frågan är då:"Hur överför vi koordinater från
det ena systemet till det andra?"
Vi kan kalla markobservatörens koordinatsystem xj där j inte är en exponent
utan ett superscript som anger nummer på koordinataxeln.Om han gör ett fyraxligt
system med tre rumsaxlar och en tidsaxel går alltså j från 1 till 4.På samma
sätt kallar vi flakobservatörens koordinatsystem xj.
Om de lägger origo i samma punkt och vrider axlarna lika gäller att systemen
sammanfaller när bilen står stilla.Om en vektor har axelprojektionerna
Aj j = 1 till 4
i markobservatörens system gäller då för axelprojektionerna i flakobservatörens
system att
Aj = Aj j = 1 till 4
vi kan skriva
4
Aj = ∑ Ajk Ak = Ajk Ak
k=1
(Om tensorkalkyl se min tekniksida Tekniksida (http://w1.877.telia.com/~u87701228))
Vi kan skriva Ajk som en transformationsmatris
1 0 0 0
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Denna överför axelprojektionerna av vektorn A oförändrade till axelprojektionerna
av vektorn A.
Om axel nr 1 är x-axeln och axel nr 4 är tidsaxel så borde det förhållandet att bilen
sätter fart och kör med hastigheten v i x-riktningen bara betyda att flakobservatörens
avstånd från punkter i x-led minskar med v gånger tid.Det innebär att Ajk blir
1 0 0 -v
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Detta var den typ av koordinattransformation som Gallilei och Newton använde.Men
den gav olika resultat när markobservatören och flakobservatören skulle tala om
vad som hände när flakobservatören använde instrumentet enl fig 1.Den stämde inte
heller med Maxwells ekvationer.
1903 föreslog Hendrik Antoon Lorentz att man skulle använda en transformationsmatris
enligt
γ 0 0 -γv/c
0 1 0 0
Ajk =
0 0 1 0
-γv/c 0 0 γ
där
γ = 1/√(1 - (v/c)2)
Och ser man på.Nu stämde det.Einstein fortsatte med att popularisera resultatet.
Vad som händer är att när markobservatören försöker se på flakobservatörens klocka
så finner han att den går för sakta.Och när flakobservatören håller upp en meterstav
i färdriktningen så finner markobservatören att den är kortare än en meter.
När markobservatören ser på strålen till spegel B säger han att gångtiden har ökat
för att strålen går längre väg.Men flakobservatören ser ingen förlängning av vägen
och ingen förlängning av gångtiden men nu kan markobservatören förklara det med att
flakobservatörens klocka går saktare.
Det samma gäller strålen till spegel A men här har dessutom avståndet till spegeln
minskat.När markobservatören ser på anordningen finner han att spegel A har kommit
närmare ljuskällan.Att flakobservatören mäter oförändrad gångtid till spegel A
beror alltså,enligt markobservatören,dels på att hans klocka går saktare dels på att
spegel A kommit närmare.
(Hoppas jag har vänt allt rätt och fått allt på rätt plats.Det är mycket att
hålla reda på och sånt är inte min starka sida.Tala om om du hittar något fel.)
Koordinattid
------------
Hittills har jag bara beskrivit det synsätt som idag är vedertaget.
När Gallilei,Kopernicus och Kepler flyttade världens centrum till solen blev
stjärnkartan mycket enklare.Det betydde inte att den heliocentriska världsbilden
i någon absolut mening var mer rätt än Ptolemaios.Och fortfarande är Ptolemaios
karta,på sätt och vis,elegantare eftersom den arbetar med cirklar som bl a Platon
ansåg vara fulländade figurer.Men den heliocentriska världsbilden blev så enkel
att vi idag kan lära ut den redan till barn på lågstadiet.
Trots att det gått c:a 100 år sedan Minkowski-rummet och Lorentz-transformen
presenterades lär vi inte ut detta på lågstadiet.Minkowskis rum-tid kräver en
viss vana vid att hantera komplexa tal och,även om några tillämpningar av
Lorentz-kontraktionen blivit allmängods,kräver Lorentz-transformatinen en viss
vana vid tensorkalkyl.
Kan vi,som Gallilei gjorde,flytta observationspunkten och få en enklare bild?
En rymdresenär som färdas bort från jorden i en riktning som vi kan kalla
x-riktningen ser hela tiden ett växande avstånd till jorden.För honom blir
x-riktningen en tidsaxel.I stället för att mäta tid med klocka kan han mäta
tid med avståndet till jorden.
Tiden har egenskaper som sammanfaller med rumskoordinater och rumskoordinater
har egenskaper som sammanfaller med tid.
Vad händer om vi säger att det förutom de vanliga tre rumsaxlarna finns en
fjärde axel som är vinkelrät mot de övriga?Vi kan inte rita ett sådant system
och vi kan inte få in alla fyra axlarna i det tredimensionella rummet men det
behöver ju inte betyda att det inte finns en sådan axel.
Om det finns en sådan axel kan vi avsätta tid efter den och kalla den för
koordinattid.De egenskaper hos tiden som inte är av koordinatkaraktär kan vi
samla i ett nytt tidsbegrepp som vi kan kalla parametertid.
Så kan vi säga att alla dessa fyra axlar har identiska egenskaper.Vi kan vrida
systemet hur vi vill och låta koordinattidsaxeln bli en rumsaxel eller låta
en rumsaxel byta plats med koordinattiden.Hur vi än flyttar och vrider
koordinatsystemet skall alla fysikaliska lagar fortsätta att gälla.Världen
kan inte veta hur vi lägger in koordinatsystem.Den beter sig likadant oavsett
hur vi ändrar koordinatsystemet.
Så antar vi att vi alla färdas med ljushastighet c i någon riktning i detta
fyraxliga koordinatsystem.
Om vi ligger stilla i rummet d v s om x- , y- och z-koordinaterna är oförändrade
betyder det att vi har lagt koordinattidsaxeln i vår färdriktning.Vi rör oss
då med ljushastighet i tidsriktningen och ligger stilla i rummet.
Det som händer när vi rör oss med hastigheten v i rummet är inte,som i Minkowski-
rummet,att vi lägger till en hastighet utan att vi vrider vår hastighetsriktning.
Vi rör oss fortfarande med ljushastighet men inte längre rakt i tidsriktningen.
Vi har vridit hastigheten så att vi fått en hastighetskomposant i rummet.
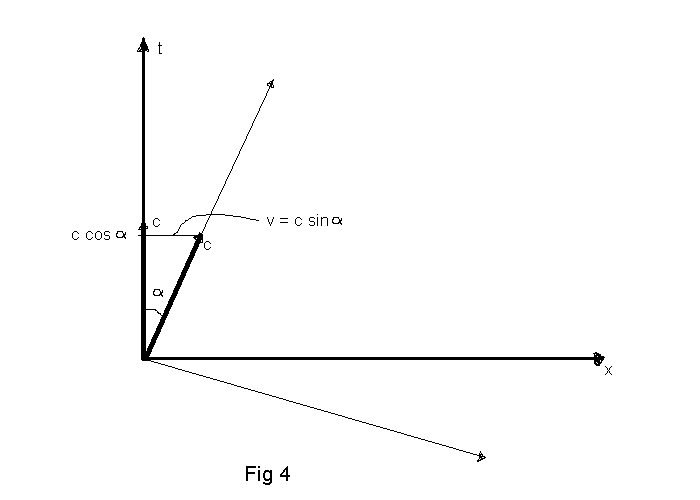 När hastigheten vrids vinkeln α får den en komposant v = c sin α i rummet
d v s i x-led och samtidigt minskar hastigheten i t-led till c cos α.Observera
att detta skiljer sig från Minkowski-rummet där komposanten i t-led inte minskar och
där vi därför får v = c tan α.
Vi har
sin α = v/c
och
cos α = √(1 - sin2 α ) = √(1 - (v/c)2) = 1/γ
vilket ju verkar lovande när det gäller att koordinattransformationer skall kunna
förklara ljushastighetsmätningar mellan system med olika hastighet.
___________________________________
-----------------------
Åter till hemsidan
När hastigheten vrids vinkeln α får den en komposant v = c sin α i rummet
d v s i x-led och samtidigt minskar hastigheten i t-led till c cos α.Observera
att detta skiljer sig från Minkowski-rummet där komposanten i t-led inte minskar och
där vi därför får v = c tan α.
Vi har
sin α = v/c
och
cos α = √(1 - sin2 α ) = √(1 - (v/c)2) = 1/γ
vilket ju verkar lovande när det gäller att koordinattransformationer skall kunna
förklara ljushastighetsmätningar mellan system med olika hastighet.
___________________________________
-----------------------
Åter till hemsidan
 B är en händelse som ligger vid
xB + i ctB
Beloppet av detta komplexa tal är B:s avstånd från origo men om vi tar realdelen
i kvadrat och imaginärdelen,inklusive i,i kvadrat får vi en sorts avstånd s enligt
sB2 = xB2 - (ctB)2
Enligt vårt vanliga vardagsspråk inträffar B vid starttiden d v s vid ct = 0.Men
eftersom den inträffar på avståndet xB når inte någon information om den
fram till tidsaxeln förrän ct = xB.
Om vi tar med i i dt i uttrycket för ds ovan blir alltså inte ds ett avstånd i vanlig
mening utan ett sorts "samtidighetsmått".
Om
xB = ctB = ctA
når informationen från B fram till tidsaxeln just när A inträffar.En observatör i
punkten A säger alltså att händelserna A och B är "samtidiga".
När Ptolemaios skulle beskriva stjärnors rörelser utgick han från sfäriska skal
som roterade runt jorden.Det var en elegant modell.Så elegant att hans världsbild
stod sig i många århundraden trots att den var mycket svårhanterlig.
Minkowski-rummet är elegant men för att tillämpa det på verkligheten får vi ta
till skohorn för att tolka begrepp som avstånd,samtidighet och tidsökning.Lite
sakadar det de fina skorna men liksom Ptolemaios fick sin stjärnkarta att
stämma fick Minkowski sin rum-tid att stämma.
Lorentz-transformen
-------------------
Om en skytt står på marken och avlossar ett gevär får kulan en utgångshastighet
som vi kan kalla vg.Oavsett vilken riktning han skjuter i får kulan
samma hastighet i förhållande till jorden.
Så sätter vi honom på ett lastbilsflak och sätter fart på bilen.Om bilen har
hastigheten vb gäller att om han skjuter framåt får kulan
utgångshastigheten i förhållande till jorden vg + vb och om han skjuter
bakåt blir utgångshastigheten i förhållande till jorden vg - vb.
Skjuter han åt sidan blir hastigheten i sidled vg.Han får då också en
hastighetskomposant i bilens körriktning.
Om ljus beter sig som gevärskulan skulle en observatör på marken som mäter
ljushastighet finna att om man ställer en strålkastare på bilflaket och mäter
hastigheten hos det ljus som kommer från den får man c + vb om
man mäter framför bilen i en framåtriktad stråle, c - vb om man
mäter bakom bilen i en bakåtriktad stråle och c om man mäter hastighet i
sidled.Strålen i sidled skulle emellertid inte gå rakt ut utan snett framåt.
Men så är det inte!Alla mätningar av ljushastigheten ger värdet c.
Det skulle kunna bero på att hastigheten alltid är konstant i förhållande
till ett ljusbärande medium på samma sätt som ljudhastigheten alltid är
konstant i förhållande till luften oberoende av hur ljudkällorna rör sig.
Om det är så kan vi göra en anordning enl fig 1 och prova att vrida den i
olika riktningar för att se om det blir någon skillnad på gångtiderna.
B är en händelse som ligger vid
xB + i ctB
Beloppet av detta komplexa tal är B:s avstånd från origo men om vi tar realdelen
i kvadrat och imaginärdelen,inklusive i,i kvadrat får vi en sorts avstånd s enligt
sB2 = xB2 - (ctB)2
Enligt vårt vanliga vardagsspråk inträffar B vid starttiden d v s vid ct = 0.Men
eftersom den inträffar på avståndet xB når inte någon information om den
fram till tidsaxeln förrän ct = xB.
Om vi tar med i i dt i uttrycket för ds ovan blir alltså inte ds ett avstånd i vanlig
mening utan ett sorts "samtidighetsmått".
Om
xB = ctB = ctA
når informationen från B fram till tidsaxeln just när A inträffar.En observatör i
punkten A säger alltså att händelserna A och B är "samtidiga".
När Ptolemaios skulle beskriva stjärnors rörelser utgick han från sfäriska skal
som roterade runt jorden.Det var en elegant modell.Så elegant att hans världsbild
stod sig i många århundraden trots att den var mycket svårhanterlig.
Minkowski-rummet är elegant men för att tillämpa det på verkligheten får vi ta
till skohorn för att tolka begrepp som avstånd,samtidighet och tidsökning.Lite
sakadar det de fina skorna men liksom Ptolemaios fick sin stjärnkarta att
stämma fick Minkowski sin rum-tid att stämma.
Lorentz-transformen
-------------------
Om en skytt står på marken och avlossar ett gevär får kulan en utgångshastighet
som vi kan kalla vg.Oavsett vilken riktning han skjuter i får kulan
samma hastighet i förhållande till jorden.
Så sätter vi honom på ett lastbilsflak och sätter fart på bilen.Om bilen har
hastigheten vb gäller att om han skjuter framåt får kulan
utgångshastigheten i förhållande till jorden vg + vb och om han skjuter
bakåt blir utgångshastigheten i förhållande till jorden vg - vb.
Skjuter han åt sidan blir hastigheten i sidled vg.Han får då också en
hastighetskomposant i bilens körriktning.
Om ljus beter sig som gevärskulan skulle en observatör på marken som mäter
ljushastighet finna att om man ställer en strålkastare på bilflaket och mäter
hastigheten hos det ljus som kommer från den får man c + vb om
man mäter framför bilen i en framåtriktad stråle, c - vb om man
mäter bakom bilen i en bakåtriktad stråle och c om man mäter hastighet i
sidled.Strålen i sidled skulle emellertid inte gå rakt ut utan snett framåt.
Men så är det inte!Alla mätningar av ljushastigheten ger värdet c.
Det skulle kunna bero på att hastigheten alltid är konstant i förhållande
till ett ljusbärande medium på samma sätt som ljudhastigheten alltid är
konstant i förhållande till luften oberoende av hur ljudkällorna rör sig.
Om det är så kan vi göra en anordning enl fig 1 och prova att vrida den i
olika riktningar för att se om det blir någon skillnad på gångtiderna.
 Om vi rör oss med hastigheten v så att spegel A ligger rakt framåt följer vi
med ljuset när det går fram i den ljusbärande etern. Ljushastigheten i
förhållande till vår anordning blir då c - v och gångtiden fram till
spegel A blir x/(c - v).Så vänder ljuset och går mot anordningens
färdriktning.Ljushastigheten i förhållande till anordningen blir
då c + v och gångtiden tillbaka från spegel A blir x/(c + v).
Om vi rör oss med hastigheten v så att spegel A ligger rakt framåt följer vi
med ljuset när det går fram i den ljusbärande etern. Ljushastigheten i
förhållande till vår anordning blir då c - v och gångtiden fram till
spegel A blir x/(c - v).Så vänder ljuset och går mot anordningens
färdriktning.Ljushastigheten i förhållande till anordningen blir
då c + v och gångtiden tillbaka från spegel A blir x/(c + v).
 I sidled går strålen snett framåt.Den går till spegel B och reflekteras så att den
återkommer när ljukällan är vid C.Om vi kallar gångtiden fram till spegel B för
t hinner spegeln gå sträckan vt innan ljuset kommer fram till den.Gångvägen blir då
sB = √(x2 + (vt)2)
och gångtiden blir
sB
t = --
c
Detta ger
(tc)2 = x2 + (vt)2
t2 (c2 - v2) = x2
x
t = ---------
c √(1 - (v/c)2)
Ljuset kommer alltså tillbaka från spegel A efter tiden
x x 2 c x 2 x 1
tA = ----- + ------ = ------- = ---- -------
c-v c+v c2 - v2 c 1 - v2/c2
och ljuset kommer tillbaka från spegel B efter tiden
2 x 2 x 1
tB = 2 t = --------------- = --- ------------- = tA √(1 - (v/c)2)
c √(1 - (v/c)2) c √(1 - (v/c)2)
tA är alltså större än tB.Hastigheten c-v ger ökad gångtid som inte helt
kompenseras av att c+v ger minskad gångtid.Och den förlusten blir större än den
förlust som den ökade gångvägen i sidled ger.
Man förlorar mer på en hastighetsminskning än man vinner på en lika stor
hastighetsökning.Antag att en person har 3 mil till jobbet och brukar köra med 90
km/tim.Det tar då 20 min d v s 40 minuter restid per dag.Om han en dag kör
80 km/tim på ditvägen tar det 22,5 minuter.Om han försöker kompensera det
genom att köra 100 km/tim på hemresan tar den 18 minuter.Hans sammanlagda
restid blir då 40,5 minuter d v s en halv minut längre än normalt.Tydligast
kan man se detta om man tänker sig att han minskar hastigheten på ditvägen
med 90 km/tim d v s går ner till hastigheten noll.Då kommer han fram först
efter oändlig tid och det kan han inte kompensera genom att köra 180 km/tim
på hemresan.
Men när Michelson och Morley försökte mäta skillnaden på gångtid i olika riktningar
fann de att den alltid var noll.Ljus beter sig tydligen varken som gevärskulor eller
ljud.
Låt oss då se lite närmare på situationen att vi har en observatör med mätanordningen
på ett bilflak och en observatör på marken.Observatören på bilflaket säger: "Jag är
världens medelpunkt.Jag står stilla.Det är klart att jag mäter samma gångtid för
ljus i alla riktningar.Att marken under bilen rör sig har ingenting med mina
mätningar att göra."
Observatören på marken säger:"Gångtiden i sidled måste ha blivit längre eftersom
ljuset nu får gå längre väg och gångtiden fram och tillbaka till spegel A måste ha
blivit ännu längre.Hur kan flakobservatören,t ex via en mobiltelefon,påstå att
gångtiderna är lika?"
När markobservatören och flakobservatören skall beskriva världen omkring sig
kan de göra upp var sitt koordinatsystem.Dessa gör de naturligtvis så att de
själva är stilla i dem.Bådas system ser likadana ut men båda ser att den andres
system rör sig med hastigheten v.Frågan är då:"Hur överför vi koordinater från
det ena systemet till det andra?"
Vi kan kalla markobservatörens koordinatsystem xj där j inte är en exponent
utan ett superscript som anger nummer på koordinataxeln.Om han gör ett fyraxligt
system med tre rumsaxlar och en tidsaxel går alltså j från 1 till 4.På samma
sätt kallar vi flakobservatörens koordinatsystem xj.
Om de lägger origo i samma punkt och vrider axlarna lika gäller att systemen
sammanfaller när bilen står stilla.Om en vektor har axelprojektionerna
Aj j = 1 till 4
i markobservatörens system gäller då för axelprojektionerna i flakobservatörens
system att
Aj = Aj j = 1 till 4
vi kan skriva
4
Aj = ∑ Ajk Ak = Ajk Ak
k=1
(Om tensorkalkyl se min tekniksida Tekniksida (http://w1.877.telia.com/~u87701228))
Vi kan skriva Ajk som en transformationsmatris
1 0 0 0
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Denna överför axelprojektionerna av vektorn A oförändrade till axelprojektionerna
av vektorn A.
Om axel nr 1 är x-axeln och axel nr 4 är tidsaxel så borde det förhållandet att bilen
sätter fart och kör med hastigheten v i x-riktningen bara betyda att flakobservatörens
avstånd från punkter i x-led minskar med v gånger tid.Det innebär att Ajk blir
1 0 0 -v
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Detta var den typ av koordinattransformation som Gallilei och Newton använde.Men
den gav olika resultat när markobservatören och flakobservatören skulle tala om
vad som hände när flakobservatören använde instrumentet enl fig 1.Den stämde inte
heller med Maxwells ekvationer.
1903 föreslog Hendrik Antoon Lorentz att man skulle använda en transformationsmatris
enligt
γ 0 0 -γv/c
0 1 0 0
Ajk =
0 0 1 0
-γv/c 0 0 γ
där
γ = 1/√(1 - (v/c)2)
Och ser man på.Nu stämde det.Einstein fortsatte med att popularisera resultatet.
Vad som händer är att när markobservatören försöker se på flakobservatörens klocka
så finner han att den går för sakta.Och när flakobservatören håller upp en meterstav
i färdriktningen så finner markobservatören att den är kortare än en meter.
När markobservatören ser på strålen till spegel B säger han att gångtiden har ökat
för att strålen går längre väg.Men flakobservatören ser ingen förlängning av vägen
och ingen förlängning av gångtiden men nu kan markobservatören förklara det med att
flakobservatörens klocka går saktare.
Det samma gäller strålen till spegel A men här har dessutom avståndet till spegeln
minskat.När markobservatören ser på anordningen finner han att spegel A har kommit
närmare ljuskällan.Att flakobservatören mäter oförändrad gångtid till spegel A
beror alltså,enligt markobservatören,dels på att hans klocka går saktare dels på att
spegel A kommit närmare.
(Hoppas jag har vänt allt rätt och fått allt på rätt plats.Det är mycket att
hålla reda på och sånt är inte min starka sida.Tala om om du hittar något fel.)
Koordinattid
------------
Hittills har jag bara beskrivit det synsätt som idag är vedertaget.
När Gallilei,Kopernicus och Kepler flyttade världens centrum till solen blev
stjärnkartan mycket enklare.Det betydde inte att den heliocentriska världsbilden
i någon absolut mening var mer rätt än Ptolemaios.Och fortfarande är Ptolemaios
karta,på sätt och vis,elegantare eftersom den arbetar med cirklar som bl a Platon
ansåg vara fulländade figurer.Men den heliocentriska världsbilden blev så enkel
att vi idag kan lära ut den redan till barn på lågstadiet.
Trots att det gått c:a 100 år sedan Minkowski-rummet och Lorentz-transformen
presenterades lär vi inte ut detta på lågstadiet.Minkowskis rum-tid kräver en
viss vana vid att hantera komplexa tal och,även om några tillämpningar av
Lorentz-kontraktionen blivit allmängods,kräver Lorentz-transformatinen en viss
vana vid tensorkalkyl.
Kan vi,som Gallilei gjorde,flytta observationspunkten och få en enklare bild?
En rymdresenär som färdas bort från jorden i en riktning som vi kan kalla
x-riktningen ser hela tiden ett växande avstånd till jorden.För honom blir
x-riktningen en tidsaxel.I stället för att mäta tid med klocka kan han mäta
tid med avståndet till jorden.
Tiden har egenskaper som sammanfaller med rumskoordinater och rumskoordinater
har egenskaper som sammanfaller med tid.
Vad händer om vi säger att det förutom de vanliga tre rumsaxlarna finns en
fjärde axel som är vinkelrät mot de övriga?Vi kan inte rita ett sådant system
och vi kan inte få in alla fyra axlarna i det tredimensionella rummet men det
behöver ju inte betyda att det inte finns en sådan axel.
Om det finns en sådan axel kan vi avsätta tid efter den och kalla den för
koordinattid.De egenskaper hos tiden som inte är av koordinatkaraktär kan vi
samla i ett nytt tidsbegrepp som vi kan kalla parametertid.
Så kan vi säga att alla dessa fyra axlar har identiska egenskaper.Vi kan vrida
systemet hur vi vill och låta koordinattidsaxeln bli en rumsaxel eller låta
en rumsaxel byta plats med koordinattiden.Hur vi än flyttar och vrider
koordinatsystemet skall alla fysikaliska lagar fortsätta att gälla.Världen
kan inte veta hur vi lägger in koordinatsystem.Den beter sig likadant oavsett
hur vi ändrar koordinatsystemet.
Så antar vi att vi alla färdas med ljushastighet c i någon riktning i detta
fyraxliga koordinatsystem.
Om vi ligger stilla i rummet d v s om x- , y- och z-koordinaterna är oförändrade
betyder det att vi har lagt koordinattidsaxeln i vår färdriktning.Vi rör oss
då med ljushastighet i tidsriktningen och ligger stilla i rummet.
Det som händer när vi rör oss med hastigheten v i rummet är inte,som i Minkowski-
rummet,att vi lägger till en hastighet utan att vi vrider vår hastighetsriktning.
Vi rör oss fortfarande med ljushastighet men inte längre rakt i tidsriktningen.
Vi har vridit hastigheten så att vi fått en hastighetskomposant i rummet.
I sidled går strålen snett framåt.Den går till spegel B och reflekteras så att den
återkommer när ljukällan är vid C.Om vi kallar gångtiden fram till spegel B för
t hinner spegeln gå sträckan vt innan ljuset kommer fram till den.Gångvägen blir då
sB = √(x2 + (vt)2)
och gångtiden blir
sB
t = --
c
Detta ger
(tc)2 = x2 + (vt)2
t2 (c2 - v2) = x2
x
t = ---------
c √(1 - (v/c)2)
Ljuset kommer alltså tillbaka från spegel A efter tiden
x x 2 c x 2 x 1
tA = ----- + ------ = ------- = ---- -------
c-v c+v c2 - v2 c 1 - v2/c2
och ljuset kommer tillbaka från spegel B efter tiden
2 x 2 x 1
tB = 2 t = --------------- = --- ------------- = tA √(1 - (v/c)2)
c √(1 - (v/c)2) c √(1 - (v/c)2)
tA är alltså större än tB.Hastigheten c-v ger ökad gångtid som inte helt
kompenseras av att c+v ger minskad gångtid.Och den förlusten blir större än den
förlust som den ökade gångvägen i sidled ger.
Man förlorar mer på en hastighetsminskning än man vinner på en lika stor
hastighetsökning.Antag att en person har 3 mil till jobbet och brukar köra med 90
km/tim.Det tar då 20 min d v s 40 minuter restid per dag.Om han en dag kör
80 km/tim på ditvägen tar det 22,5 minuter.Om han försöker kompensera det
genom att köra 100 km/tim på hemresan tar den 18 minuter.Hans sammanlagda
restid blir då 40,5 minuter d v s en halv minut längre än normalt.Tydligast
kan man se detta om man tänker sig att han minskar hastigheten på ditvägen
med 90 km/tim d v s går ner till hastigheten noll.Då kommer han fram först
efter oändlig tid och det kan han inte kompensera genom att köra 180 km/tim
på hemresan.
Men när Michelson och Morley försökte mäta skillnaden på gångtid i olika riktningar
fann de att den alltid var noll.Ljus beter sig tydligen varken som gevärskulor eller
ljud.
Låt oss då se lite närmare på situationen att vi har en observatör med mätanordningen
på ett bilflak och en observatör på marken.Observatören på bilflaket säger: "Jag är
världens medelpunkt.Jag står stilla.Det är klart att jag mäter samma gångtid för
ljus i alla riktningar.Att marken under bilen rör sig har ingenting med mina
mätningar att göra."
Observatören på marken säger:"Gångtiden i sidled måste ha blivit längre eftersom
ljuset nu får gå längre väg och gångtiden fram och tillbaka till spegel A måste ha
blivit ännu längre.Hur kan flakobservatören,t ex via en mobiltelefon,påstå att
gångtiderna är lika?"
När markobservatören och flakobservatören skall beskriva världen omkring sig
kan de göra upp var sitt koordinatsystem.Dessa gör de naturligtvis så att de
själva är stilla i dem.Bådas system ser likadana ut men båda ser att den andres
system rör sig med hastigheten v.Frågan är då:"Hur överför vi koordinater från
det ena systemet till det andra?"
Vi kan kalla markobservatörens koordinatsystem xj där j inte är en exponent
utan ett superscript som anger nummer på koordinataxeln.Om han gör ett fyraxligt
system med tre rumsaxlar och en tidsaxel går alltså j från 1 till 4.På samma
sätt kallar vi flakobservatörens koordinatsystem xj.
Om de lägger origo i samma punkt och vrider axlarna lika gäller att systemen
sammanfaller när bilen står stilla.Om en vektor har axelprojektionerna
Aj j = 1 till 4
i markobservatörens system gäller då för axelprojektionerna i flakobservatörens
system att
Aj = Aj j = 1 till 4
vi kan skriva
4
Aj = ∑ Ajk Ak = Ajk Ak
k=1
(Om tensorkalkyl se min tekniksida Tekniksida (http://w1.877.telia.com/~u87701228))
Vi kan skriva Ajk som en transformationsmatris
1 0 0 0
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Denna överför axelprojektionerna av vektorn A oförändrade till axelprojektionerna
av vektorn A.
Om axel nr 1 är x-axeln och axel nr 4 är tidsaxel så borde det förhållandet att bilen
sätter fart och kör med hastigheten v i x-riktningen bara betyda att flakobservatörens
avstånd från punkter i x-led minskar med v gånger tid.Det innebär att Ajk blir
1 0 0 -v
0 1 0 0
Ajk =
0 0 1 0
0 0 0 1
Detta var den typ av koordinattransformation som Gallilei och Newton använde.Men
den gav olika resultat när markobservatören och flakobservatören skulle tala om
vad som hände när flakobservatören använde instrumentet enl fig 1.Den stämde inte
heller med Maxwells ekvationer.
1903 föreslog Hendrik Antoon Lorentz att man skulle använda en transformationsmatris
enligt
γ 0 0 -γv/c
0 1 0 0
Ajk =
0 0 1 0
-γv/c 0 0 γ
där
γ = 1/√(1 - (v/c)2)
Och ser man på.Nu stämde det.Einstein fortsatte med att popularisera resultatet.
Vad som händer är att när markobservatören försöker se på flakobservatörens klocka
så finner han att den går för sakta.Och när flakobservatören håller upp en meterstav
i färdriktningen så finner markobservatören att den är kortare än en meter.
När markobservatören ser på strålen till spegel B säger han att gångtiden har ökat
för att strålen går längre väg.Men flakobservatören ser ingen förlängning av vägen
och ingen förlängning av gångtiden men nu kan markobservatören förklara det med att
flakobservatörens klocka går saktare.
Det samma gäller strålen till spegel A men här har dessutom avståndet till spegeln
minskat.När markobservatören ser på anordningen finner han att spegel A har kommit
närmare ljuskällan.Att flakobservatören mäter oförändrad gångtid till spegel A
beror alltså,enligt markobservatören,dels på att hans klocka går saktare dels på att
spegel A kommit närmare.
(Hoppas jag har vänt allt rätt och fått allt på rätt plats.Det är mycket att
hålla reda på och sånt är inte min starka sida.Tala om om du hittar något fel.)
Koordinattid
------------
Hittills har jag bara beskrivit det synsätt som idag är vedertaget.
När Gallilei,Kopernicus och Kepler flyttade världens centrum till solen blev
stjärnkartan mycket enklare.Det betydde inte att den heliocentriska världsbilden
i någon absolut mening var mer rätt än Ptolemaios.Och fortfarande är Ptolemaios
karta,på sätt och vis,elegantare eftersom den arbetar med cirklar som bl a Platon
ansåg vara fulländade figurer.Men den heliocentriska världsbilden blev så enkel
att vi idag kan lära ut den redan till barn på lågstadiet.
Trots att det gått c:a 100 år sedan Minkowski-rummet och Lorentz-transformen
presenterades lär vi inte ut detta på lågstadiet.Minkowskis rum-tid kräver en
viss vana vid att hantera komplexa tal och,även om några tillämpningar av
Lorentz-kontraktionen blivit allmängods,kräver Lorentz-transformatinen en viss
vana vid tensorkalkyl.
Kan vi,som Gallilei gjorde,flytta observationspunkten och få en enklare bild?
En rymdresenär som färdas bort från jorden i en riktning som vi kan kalla
x-riktningen ser hela tiden ett växande avstånd till jorden.För honom blir
x-riktningen en tidsaxel.I stället för att mäta tid med klocka kan han mäta
tid med avståndet till jorden.
Tiden har egenskaper som sammanfaller med rumskoordinater och rumskoordinater
har egenskaper som sammanfaller med tid.
Vad händer om vi säger att det förutom de vanliga tre rumsaxlarna finns en
fjärde axel som är vinkelrät mot de övriga?Vi kan inte rita ett sådant system
och vi kan inte få in alla fyra axlarna i det tredimensionella rummet men det
behöver ju inte betyda att det inte finns en sådan axel.
Om det finns en sådan axel kan vi avsätta tid efter den och kalla den för
koordinattid.De egenskaper hos tiden som inte är av koordinatkaraktär kan vi
samla i ett nytt tidsbegrepp som vi kan kalla parametertid.
Så kan vi säga att alla dessa fyra axlar har identiska egenskaper.Vi kan vrida
systemet hur vi vill och låta koordinattidsaxeln bli en rumsaxel eller låta
en rumsaxel byta plats med koordinattiden.Hur vi än flyttar och vrider
koordinatsystemet skall alla fysikaliska lagar fortsätta att gälla.Världen
kan inte veta hur vi lägger in koordinatsystem.Den beter sig likadant oavsett
hur vi ändrar koordinatsystemet.
Så antar vi att vi alla färdas med ljushastighet c i någon riktning i detta
fyraxliga koordinatsystem.
Om vi ligger stilla i rummet d v s om x- , y- och z-koordinaterna är oförändrade
betyder det att vi har lagt koordinattidsaxeln i vår färdriktning.Vi rör oss
då med ljushastighet i tidsriktningen och ligger stilla i rummet.
Det som händer när vi rör oss med hastigheten v i rummet är inte,som i Minkowski-
rummet,att vi lägger till en hastighet utan att vi vrider vår hastighetsriktning.
Vi rör oss fortfarande med ljushastighet men inte längre rakt i tidsriktningen.
Vi har vridit hastigheten så att vi fått en hastighetskomposant i rummet.
 När hastigheten vrids vinkeln α får den en komposant v = c sin α i rummet
d v s i x-led och samtidigt minskar hastigheten i t-led till c cos α.Observera
att detta skiljer sig från Minkowski-rummet där komposanten i t-led inte minskar och
där vi därför får v = c tan α.
Vi har
sin α = v/c
och
cos α = √(1 - sin2 α ) = √(1 - (v/c)2) = 1/γ
vilket ju verkar lovande när det gäller att koordinattransformationer skall kunna
förklara ljushastighetsmätningar mellan system med olika hastighet.
___________________________________
-----------------------
Åter till hemsidan
När hastigheten vrids vinkeln α får den en komposant v = c sin α i rummet
d v s i x-led och samtidigt minskar hastigheten i t-led till c cos α.Observera
att detta skiljer sig från Minkowski-rummet där komposanten i t-led inte minskar och
där vi därför får v = c tan α.
Vi har
sin α = v/c
och
cos α = √(1 - sin2 α ) = √(1 - (v/c)2) = 1/γ
vilket ju verkar lovande när det gäller att koordinattransformationer skall kunna
förklara ljushastighetsmätningar mellan system med olika hastighet.
___________________________________
-----------------------
Åter till hemsidan