Leif Andersson Henriksbergsvägen 104 136 67 Vendelsö 2013-03-25
2012-11-16 startade jag en tråd på Flashback med rubruken "Krökt rum" i forumet för
"Fysik,matematik och teknologi". Det blev 300 svar och 16000 visningar. Jag har här plockat ut några
av mina inlägg. En del är svar på andra inlägg och de kan bli lite ofullständiga som fristående inlägg
men jag tror att de är begripliga.
2012-11-16
Under en solförmörkelse kan man se att ljuset från en stjärna kröks när det passerar nära solen
genom solens gravitationsfält.
På ett töjbart papper kan jag rita upp den krökta ljusstrålen och lägga in den i ett rätvinkligt och
rätlinjigt koordinatsystem. När jag så tittar på bilden kan jag säga mig: "En ljusstråle måste vara
rak". Så tar jag tag i papperet och töjer det så att ljusstrålen blir rak men då blir mina
koordinataxlar krokiga.
Jag har då fått två bilder av ljusstrålen, en med krokig ljusstråle och raka koordinataxlar och en med
rak ljusstråle och krokiga koordinataxlar. Att jag ändrar bilden av ljusstrålen påverkar naturligtvis
inte den verkliga ljusstrålen den kröks i solens gravitationsfält oavsett hur jag avbildar krökningen.
Om jag vore van vid att hantera kroklinjiga koordinatsystem skulle det kanske vara lämpligt att
använda krokiga koordinataxlar och raka ljusstrålar. Men det är jag inte. Jag har svårt att hantera
begrepp som avstånd, riktningsvinkel och projektion i kroklinjiga koordinatsystem. Även om jag
naturligtvis kan använda en del matematiska verktyg saknar jag den intuitiva känsla som gör att jag
kan se nya samband och möjligheter.
En bild med rätlinjigt koordinatsystem och krokiga ljusstrålar är konstig eftersom ljusstrålarna inte är
raka. Den konstigheten kan jag avhjälpa genom att kröka koordinataxlarna men det ger en ny bild
som är minst lika konstig. Det är inte uppenbart någon fördel med att använda ett kroklinjigt
koordinatsystem. Frågan är om det på något sätt ger en förenklad beskrivning av något annat. Så
vitt jag kan se gör det inte det.
Som jag ser det kan man välja mellan att beskriva ljusstrålar som krokiga i rakt rum eller som raka i
krökt rum. Jag har inte funnit någon fördel med att använda beskrivningen med krökt rum.
Jag KAN men MÅSTE INTE se en bild av världen där mina koordinataxlar är krökta men ljusstrålar är
raka. Jag kan se världen via en bucklig skrattspegel som gör ljusstrålar raka. Om jag vet hur spegeln
är bucklig är det inget fel på den bilden. Den är lika rätt som en bild i en plan spegel där ljusstrålar
är krökta. Frågan är bara vilken bild jag tycker är lättast att hantera.
__________________
2012-11-17
Om jag avbildar världen på ett rätlinjigt koordinatsystem blir ljusstrålar krokiga, bland annat när de
passerar ett gravitationsfält. Det innebär att ljushastigheten varierar. Den är lägre längs innerkurvan
än längs ytterkurvan.
Hastighet anges i meter per sekund. I stället för att säga att hastigheten varierar kan jag naturligtvis
säga att hastigheten är konstant men metern och/eller sekunden varierar så att kvoten mellan dem
alltid blir konstant. I mitt fyrdimensionella koordinatsystem låter jag någon längdkoordinat vara
beroende av (alltså icke-ortogonal mot) tiden. Jag kröker alltså till exempel x-axeln i tidsled.
Eftersom hastigheten då blir lika i alla delar av ljusstrålen blir den rak.
__________________
2012-11-18
Jag kan se på min värld på flera olika sätt som alla är korrekta och användbara. Följande exempel
kanske visar vad jag menar.
När jag kör med min bil kan jag se det som att jordytan ligger stilla och drivhjulen förflyttar bilen dit
jag vill komma (geocentrisk världsbild). Men jag kan också se det som att bilen står stilla och
drivhjulen snurrar jordkloten så att jag kommer dit jag vill (egocentrisk världsbild). Båda synsätten
är helt korrekta och användbara. Den geocentriska världsbilden är vanligare och ofta är den lättare
att använda men ibland använder jag den egocentriska för att den stämmer bra med vad jag ser
genom vindrutan.
Att jag kan välja mellan att avbilda världen på ett plant eller krökt rum är inte konstigare än att jag
kan välja geocentrisk eller egocentrisk världsbild.
Möjligheten att välja en annan världsbild ger oss ibland möjlighet att se nya möjligheter. Det är inte
något fel utan tvärtom önskvärt att vi ser på vår värld på lite olika sätt. Den tid är över (hoppas jag)
när man riskerade att bli bränd på bål om man använde en heliocentrisk världsbild.
__________________
2012-11-20
Frågan är: "Har verkligheten en egen metrik?" En metrik som är den enda rätta.
Kanske. Men efter att ha använt Minkowskis metrik i ett halvt sekel har jag blivit allt mer övertygad
om att den ligger inte närmare verklighetens än min vardagsmetrik (även om den naturligtvis ibland
är användbar). I stället har jag alltmer blivit övertygad om att verkligheten har ingen egen metrik.
Mitt enda sätt att få någon uppfattning om min omgivning är att använda mina sinnen för att avbilda
världen på en världsbild som kan ingå i mitt sätt att tänka. Det kan jag göra på många olika sätt som
jag kan prova genom att jämföra med nya bilder av verkligheten. Så vitt jag kan se finns det inte
något sätt som är unikt genom att det alltid stämmer bättre än andra avbildningar. Vi kan inte
komma fram till den enda rätta bilden som påven kan stadfästa och ge oss den sanna bilden av
verkligheten.
__________________
2012-11-21
Att det inte finns kängurur i Sverige innebär inte att man kan dra slutsatsen att det inte finns
kängurur. Men man kan inte heller dra slutsatsen att det finns kängurur. Men om du har en känguru
tittar jag gärna på den för att kunna ta ställning till frågan.
Jag föreslår att du tar fram ett exempel på användning av minkowskimetrik. Kanske något i stil med
sambandet mellan elektrisk och magnetisk kraftverkan, fjärrstyrning av rymdfarkoster eller hantering
av GPS-signaler. Så kan vi diskutera frågan om man inte bara kan utan måste använda
minkowskimetrik.
Fram med kängurun!
__________________
2012-11-22
Jag kan avbilda H punkter i verkligheten på H bildpunkter i en världsbild oavsett hur bildpunkterna är
ordnade. När verkligheten förändras avspeglas det i världsbilden. När vi finner sätt att ordna
världsbilden så att sådana förändringar blir lätthanterliga och igenkännbara anser vi att världsbilden
beskriver verkligheten. Men egentligen vet vi då ingenting annat om verkligheten än att där
förekommer fenomen som kan beskrivas på lätthanterligt sätt i en viss världsbild. Det utesluter inte
att de kan vara ännu lättare att hantera i någon annan världsbild.
På Ptolemaios tid trodde man att planetbanor måste beskrivas med cirklar och med Jorden i
centrum. Han gjorde en stjärnkarta med detta som utgångspunkt och fick den att stämma med
observationer. Detta sågs som bevis för att världen var geocentrisk och cirkelbaserad. Så visade det
sig att elliptiska banor runt Solen gav en enklare världsbild. Men världen är varken egocentrisk,
geocentrisk, heliocentrisk eller fixstjärneförankrad. Det är inte världen utan bilden av världen som vi
kan förankra.
Om jag väljer metrik kan jag ju göra det så att det blir mycket krångligt (men inte omöjligt) att
beskriva de fenomen jag observerar. Jag har då gjort ett olämpligt men inte otillåtet val av metrik.
Jag tror att det är viktigt att vi kommer ifrån tvärsäkra påståenden om hur världen ÄR. Det vi kan
använda i våra tankar är våra världsbilder där vi kan beskriva de fenomen som vi möter. Och att vi
kan använda olika världsbilder är inte konstigare än att vi ibland kan avbilda vår omvärld med en
karta och ibland med ett fotografi. Två olika bilder av samma verklighet. Och en förändring i
verkligheten kan beskrivas som en förändring på kartan eller som en förändring i fotografit. Båda
metoderna kan vara användbara.
__________________
2012-11-24
För 150 år sedan var det självklart att alla mätte med samma meter och samma sekund. Så släppte
man kravet att metern och sekunden alltid skulle vara oförändrad och sa i stället att det skulle finnas
en hastighet (ljushastigheten) som alltid var oförändrad. Så kan man göra. Det visade sig också att
det fungerade och det gav en del nya användbara synsätt.
Men om inte metern och sekunden alltid är oförändrad är det viktigt att man talar om vilken meter
och vilken sekund man mäter med.
Om en ljusstråle böjs kan jag säga att metern blir kortare längs innerkurvan så att den blir lika
många meter som ytterkurvan. Då går ljuset lika många meter längs innerkurvan som det gör längs
ytterkurvan och ljushastigheten blir lika längs innerkurvan och ytterkurvan.
Men hur mäter jag längs innerkurvan? Jag kan inte åka till solen med en meterstav för att den skall
krympa till den lokala metern.
Genom att mäta ljusstrålens bredd och krökning kan jag beräkna innerkurvans och ytterkurvans
längd. Detta är en helt korrekt längdmätning som ger mig innerkurvans och ytterkurvans längd mätt i
min meter. Dessa längder blir olika och om jag dividerar dem med gångtiden för att få fram
ljushastigheten får jag olika värden på ljushastigheten. Jag har alltså gjort en helt korrekt mätning
som visar att ljushastigheten uttryckt som kvoten mellan längden mätt med min meter och tiden
mätt med min sekund blir olika vid innerkurvan och ytterkurvan. Om jag vill kan jag ju sedan räkna
om metern längs innerkurvan så att ljushastigheten blir konstant men det ändrar inte det faktumatt
jag fått olika ljushastigheter när jag använde min meter.
Det är också tänkbart att gångtiden blir olika. Att fotoner som går längs innerkanten kommer fram
fortare. Om det är så borde man kunna få interferensfenomen mellan strålens inre och yttre kant.
Jag tror (men vet inte) att man kan utesluta den möjligheten.
__________________
2012-11-25
Vi är tydligen inne på samma tankebana. Att gravitation är en uppbromsning av rumtiden. Men
frågan blir då vad som menas med bromsning av rumtiden. Som jag ser det behöver vi dela upp
tidsbegreppet i två delar, parametertid och koordinattid. Och vi behöver tala om ett flöde som kan
bromsas. Det är det jag, trots alla tabun, försöker kalla eter och etervind.
__________________
2012-11-26
Jag är långt ifrån färdig med spinn-teorier men jag har en inledande fråga. Talar du om att det
magnetiska fältet kan ses som en relativistisk korrektion av det elektriska?
När den lokala metern krymper med Lorentzkontraktionen ändras laddningsfördelningen så att det
elektriska fältet förändras. Denna förändring är det som vi kallar det magnetiska fältet.
Som jag ser det färdas jag med ljushastighet genom en fyrdimensionell värld. Färdriktningen kallar
jag koordinattidsriktning. Om två system rör sig i förhållande till varandra kommer deras
koordinattidsaxlar att bilda en vinkel. Sinus för denna vinkel är det ena systemets hastighet i
förhållande till det andra och cosinus är Lorentzkontraktionen. Tillämpar jag detta synsätt på det
elektriska fältet får jag samma resultat, alltså det magnetiska fältet, som vid en relativistisk
korrektion.
__________________
2012-11-26
Ljudhastighet bestäms av luftens elasticitet och täthet. Maxwells ekvationer visar att ljushastigheten
på liknande sätt bestäms av det ljusbärande mediets kapacitans och induktans. Vi har nu i hundra år
lyckats med konststycket att påstå att det är ingenting som har kapacitans och induktans. I normalt
språkbruk betyder "ingenting" avsaknad av alla egenskaper utom egenskapen att inte finnas. Men
trots att vi kan mäta ljushastighet och kapacitans och induktans var för sig och se att allt stämmer
har vi tabubelagt allt tal om att ljushastighet skulle vara knuten till egenskaper hos ett bärande
medium.
Hela optiken bygger på att vi kan påverka ljus genom att ändra kapacitans och/eller induktans hos
det ljusbärande mediet och därigenom ändra ljushastigheten.
Du har väl rätt i att det inte är något som vi kommer att lösa men jag tror att ett stort steg på vägen
är om vi kunde bryta ett par meningslösa tabun.
Jag tror att en diskussion kring egenskaper hos ett ljusbärande medium skulle kunna ge oss en rad
nya infallsvinklar.
__________________
2012-11-28
Begreppet "spinn" är nära kopplat till begreppet "magnetiskt dipolmoment". När vi mäter spinn
mäter vi magnetiskt dipolmoment.
Det elektriska och magnetiska fältet är knutna till varandra via div och curl som i Maxwells ekvationer
(som ju är en generalisering av Kirchhoffs lagar).
I två dimensioner ger curl en skalar. I tre dimensioner en vektor och i fyra dimensioner en andra
ordningens tensor, det vill säga en 4x4-matris.
Ett skäl till att jag vill använda eterbegreppet är att jag då kan knyta div och curl till något som
divergerar och roterar. Detta passar utmärkt för mitt bondförstånd. Tredimensionell curl blir ju
åskådlig men jag har svårt att se något bra sätt att uppfatta fyrdimensionell curl. Nästan allt jag
hittat om curl handlar om tre dimensioner. Har du (eller någon annan) något tips om något bra om
fyrdimensionell curl?
När det gäller kvantisering av spinn har jag en svag aning om att man brukar använda två sätt, med
och utan relativitetsteori. Men nu hittar jag inte något om det. Jag skall läsa ditt nya inlägg närmare.
Du kanske har svarat på den frågan.
Ännu har jag inte hittat kängurun men jag kan inte heller utesluta att den finns. Jag fortsätter att
leta.
__________________
2012-12-01
Ditt förslag att åskådliggöra curl genom att multiplicera med en vektor är briljant. Ofta är man ju
intresserad av en viss riktning. Man kan till exempel se en rotation kring koordinattidsaxeln, det vill
säga en rotation utan någon rumslig rotationsaxel.En sådan rotation får ett värde och en
rotationsriktning (högervarv eller vänstervarv). Det påminner om elektrostatisk kraftverkan. Om vi
kunde knyta gravitation till div och elektrostatisk kraftverkan till curl skulle vi kunna få en riktigt snygg
världsbild. En världsbild som blir så åskådlig att man kan presentera den redan på gymnasienivå och
därmed få den allmänt spridd.
Dit är det förstås långt. Men även en läng resa börjar med ett litet steg. Och en resa bör ha ett
avlägset mål.
__________________
2012-12-05
Du behöver naturligtvis inte använda eterbegreppet om du inte vill. Jag kan bara berätta om min
världsbild som, så vitt jag kunnat finna, inte strider mot vad vi vet om världen. Den som vill kan ta till
sig den helt eller delvis och den som inte vill kan strunta i den eller som du ibland gör, beskriva
alternativa synsätt.
Jag ser en fyrdimensionell värld där koordinattiden är den fjärde riktningen. Koordinattiden skiljer sig
inte från rummet på annat sätt än att det är min färdriktning. Jag och min omgivning svävar i en eter
som blåser med ljushastighet i koordinattidsriktningen. Etern har egenskapen att den, med ändlig
hastighet kan bära information. Jag kallar den information om en händelse som etern bär för
händelsens bild. För avlägsna händelser är händelsens bild den enda information om händelsen som
når mig. Jag kan alltså inte veta något om en avlägsen händelse förrän dess bild når mig. Det
inträffar när koordinattidsavståndet är lika med rumsavståndet, det vill säga då Minkowskiavståndet
blir noll. Eftersom händelsens bild är den enda information om händelsen som når mig kan jag i
många fall ersätta händelsen med händelsens bild. För händelsens bild gäller Minkowski-metriken
men det blir en detalj i ett större sammanhang.
Ett problem med att ersätta en händelse med händelsens bild är att när Minkowskiavståndet blir noll
är det för sent att påverka händelsen. När vi nu ger oss ut i rymden med fjärrstyrda farkoster
behöver vi en betydligt bättre kunskap om den eter där vi skickar och tar emot signaler.
Redan när man på 1950-talet läste om Heaviside-skikt och lyssnade på avlägsna radiostationer med
fading insåg man att man inte kunde förneka en eter. Signalen från sändarantennen var stabil men
den svajade vid mottagarantennen. Mellan antennerna måste alltså finnas något som bar signalen
och omvandlade en stabil signal till en svajig. Detta något hade man redan döpt till eter och det var
meningslöst att försöka döpa om det.
__________________
2012-12-09
Ännu ett försök att tala om hur jag ser på min värld.
Med dt, dx, dy och dz menar jag avstånd i t-led, x-led, y-led och z-led.
Avslutande siffra är en exponent. dt2 betyder alltså dt i kvadrat.
När jag kommer till en vägkorsning kan jag se att en bil blockerar korsningen. Att jag ser bilen
betyder att dess bild har nått mig, alltså att Minkowskiavståndet är noll. Det innebär att dt2-dx2-dy2-
dz2 = 0. Men det behöver inte betyda att jag krockar med bilen. Jag väntar tills bilen lämnat
korsningen och kör igenom så att jag får samma rumskoordinater som bilen hade. Jag kan alltså ha
samma rumskoordinater utan att krocka. Jag kan alltså varken använda Minkowskiavståndet eller
rumsavståndet för att avgöra om jag håller på att krocka.
Om jag krockar blir dt2+dx2+dy2+dz2 = 0. Det är detta villkor jag kan använda för att avgöra om
jag håller på att krocka. Jag kallar dt2+dx2+dy2+dz2 för kvadraten på det reella avståndet.
Minkowskimetriken använder dt2-dx2-dy2-dz2 som invariant. Jag kallar metriken med dt2+dx2+dy2
+dz2 som invariant för reell metrik.
För att avgöra om jag håller på att krocka måste jag använda reell metrik. Den reella metriken är så
självklar att vi alla använder den utan att försöka formulera den för att använda den för beräkningar.
Det naturliga urvalet sållar snabbt bort dem som försöker basera sitt handlande i korsningen på
Minkowskimetrik. Därmed inte sagt att Minkowskimetriken inte är användbar i andra sammanhang.
Vad jag försöker säga är alltså:
Använd reell metrik för händelser.
Använd Minkowskimetrik för händelsers bild.
Den reella metriken och Minkowskimetriken kompletterar varandra. Den ena kan inte ersätta den
andra.
__________________
2012-12-10
Vi har tydligen olika definitioner på begreppet "medium". För mig är ett medium något där något kan
utbreda sig. Till det lägger du tydligen krav på att man skall kunna förankra läge i ett medium på
något annat sätt än i ett fält.
En vattenyta är ett utbredningsmedium för vattenvågor. När jag jobbade på Flygförvaltningen
pratade piloterna ibland om problemet att landa på sjön vid bleke. Vattenytan syns inte och erbjuder
inga referenspunkter. Man kan alltså inte förankra något läge i den. Jag har vid några tillfällen
påpekat att bleke i universum kallas för Nirvana. Eftersom vattenytan inte syns vid bleke kan man
naturligtvis hävda att den inte finns. Att vattenvågor inte utbreder sig i vattenytan utan i ett
massgravitationsfält. Men när pontonerna träffar vattenytan blir resultatet mycket påtagligt.
Du har naturligtvis rätt i att vi kan säga fält i stället för eter men jag ser inte varför det skulle vara
bättre. Alternativet är ju att tilldela etern de egenskaper som enligt ditt sätt att se skiljer den från
fältet.
__________________
2012-12-13
ag skall försöka ge min syn på eterbegreppet.
Ljud utbreder sig i luft. Men jag kan också säga att ljud utbreder sig i ett
tryck-impuls-fält. I tryck-impuls-fältet kan jag formulera motsvarigheten till
Maxwells ekvationer. Med dem kan jag ange en ljudhastighet i förhållande till
fältet. Det är uppenbart att tryck-impuls-fältet är knutet till luften. Jag hör
när man spikar på andra sidan sundet och jag märker att ljudet ändras när det
blåser. Ljud följer alltså med luften när den rör sig. Men om jag befinner mig
i en ballongkorg blir det svårare att se om tryck-impuls-fältet är knutet till
luften. Jag svävar ju i luften så att jag alltid ligger stilla i förhållande
till omgivande luft.
För att avgöra om jag rör mig i förhållande till luften en bit ifrån ballongen
kan jag släppa ut en liten provballong som får sväva i luften. Om jag rör mig
i förhållande till provballongen tyder det på att jag rör mig i förhållande
till luften kring provballongen. Om ljud passerar provballongen kan jag då
studera hur detta ljud påverkas av luftrörelsen vid provballongen.
Hur blir det då med ljus?
Som jag ser det svävar jag i en eter som blåser i koordinattidsriktningen. Jag
ligger alltså alltid stilla i förhållande till den eter som omger mig. Hur skall
jag då kunna avgöra om ljus följer med en eter som rör sig i förhållande till mig?
Jag måste ju hitta en eter som blåser i någon annan riktning än min
koordinattidsriktning.
För att se hur etern blåser kan jag låta ett provföremål sväva i rymden. När det
kommer i närheten av solen tar det fart in mot solen vilket tyder på att etervinden
där har en rumskomposant in mot solen. Om ljus följer med etern när den rör sig
borde ljuset ändra riktning när det passerar solen. Det gör det också.
Visst finns det skillnader mellan luft och eter. Etern tycks till exempel inte ha
någon friktion. Och det är inte helt självklart hur samband mellan eterrörelser
och fotonrörelser ser ut. När vi nu utvidgar vår intressesfär till att omfatta en
allt större rymd blir frågor kring eterns egenskaper allt viktigare. Den diskussionen
underlättas inte av att vi undviker att använda eterbegreppet.
__________________
2012-12-14
Jag kan växelverka med händelse A på två sätt. Antingen direkt eller indirekt på avstånd. Indirekt
växelverkan förmedlas via bild. Det innebär att bilden av mig påverkar A eller att bilden av A
påverkar mig.
Lorentz, Einstein och Minkowski beskrev ett sätt att hantera indirekt växelverkan. Minkowskimetriken
fungerar utmärkt för att hantera indirekt växelverkan. Den indirekta växelverkan är ett fenomen som
jag upplever och minkowskimetriken beskriver alltså något som jag upplever och har behov av att
beskriva. Och så länge jag använder den för att beskriva indirekt växelverkan uppfyller den alla krav
på verklighetsankytning och logik.
Men indirekt växelverkan är bara en del av min värld. För den mest basala handlingen av alla, att
jag stoppar mat i munnen och tuggar den, handlar det inte om indirekt växelverkan. Det är bara
genom direkt växelverkan som jag kan tillgodogöra mig maten.
När jag försöker använda minkowskimetrik för direkt växelverkan finner jag att den fungerar dåligt.
Att minkowskiavståndet till A blir noll betyder att bilden av A har nått mig men det säger ingenting
om hur nära direkt växelverkan jag är. Jag behöver komplettera minkowskimetrikens beskrivning av
indirekt växelverkan med en beskrivning av direkt växelverkan.
Jag behöver ett linjeelement, alltså ett avstånd ds som anger hur långt jag är från växelverkan. För
indirekt växelverkan blir då ds2 = dt2-dx2-dy2-dz2 och för direkt växelverkan blir det ds2 = dt2+dx2
+dy2+dz2.
För att hantera minkowskimetriken har vi utvecklat en rad matematiska verktyg. Visserligen lär
Einstein ha sagt: "Sen matematikerna fick tag på relativitetsteorin förstår jag den inte själv". Men
det är ingen tvekan om att vi lärt oss en hel del på vägen.
När det gäller en metrik för direkt växelverkan brukar vi se den som så självklar att vi inte bryr oss
om att formulera den på ett matematiskt språk. Jag tror att det skulle vara givande att försöka göra
det.
__________________
2012-12-16
För att klara min vardag behöver jag någon uppfattning av vad som är tid och vad som är längd.
Och jag behöver ett avståndsbegrepp som hjälper mig att prioritera de händelser som kräver
åtgärd. För mig är en avlägsen och alltså lågprioriterad händelse en händelse som inträffat långt
borta och/eller för länge sedan. Jag behöver alltså ett avståndsbegrepp som växer både med tid och
längd. Detta är inte något onödigt synsätt. Det är själva grunden för mitt sätt att hantera min
omvärld.
I många fall är tidförlopp och längdförflyttningar oberoende av varandra. Jag kan ange
tidsförflyttningar längs en tidsaxel (t) och längdförflyttningar längs en längdaxel (x). Om
de är oberoende av varandra lägger jag dem i rät vinkel så att projektionen av x-axeln på tidsaxeln
blir noll. Men om två system rör sig i förhållande till varandra blir inte tidsförlopp och
längdförflyttningar oberoende av varandra. När jag åker tåg kan jag ange avstånd till nästa station i
km eller i minuter.
Galileii transformation mellan två system som rör sig i förhållande till varandra var en
parallellförskjutning. Den innebar att båda systemen behöll samma riktning på t-axeln och samma
riktning på x-axeln. Men det kräver att information kan gå oändligt snabbt mellan systemen. Om det
finns en högsta möjliga hastighet för information blir inte t-axeln och x-axeln längre vinkelräta.
Lorentztransformen ger inte en ortogonal transformation. Den vrider x-axeln så att vinkeln mellan t-
axel och x-axel blir a i stället för 90 grader. Och cos(90-a) blir Lorentzkontraktionen.
Ett annat sätt att hantera detta är att se på två system A och B där B erhålls genom att man vrider
A. Att B rör sig i förhållande till A innebär alltså att B:s tidsaxel (Bt) vridits i förhållande till A:s (At).
Man kan då ha Ax vinkelrät mot At och Bx vinkelrät mot Bt men Bx blir inte vinkelrät mot At.
En observatör i A lägger in världen i ett koordinatsystem där Ax är vinkelrät mot At. En observatör i
B lägger in världen i ett koordinatsystem där Bx är vinkelrät mot Bt. Lorentztransformen
transformerar alltså inte A till B-observatörens koordinatsystem utan till A-obsrevatörens bild av B-
observatörens koordinatsystem.
Som jag ser det har en transformation direkt från A till B en stor fördel eftersom såväl A-
observatören som B-observatören kan använda den reella metrik som jag använder till vardags.
Frågan är om den på något sätt strider mot vad vi har observerat. Så vitt jag kunnat finna gör den
inte det men jag har naturligtvis inte räknat igenom alla tänkbara fall. Det kanske finns någon
känguru?
En annan fördel med detta synsätt är att det antyder en öppning i tidsled mot en mycket större värld
än den som vi idag upplever. Ungefär som när man på 1500-talet började förstå att vi omgavs av en
åtkomlig rymd. Men man ser förstås bara det man försöker se.
Det är inget fel på Minkowskimetriken. Vi har använt den i mer än hundra år och den fungerar för
sitt ändamål. Men det är sällan den används. Orsaken är att den är oanvändbar när det gäller att
prioritera bland vardagens händelser. För det behöver jag ett avstånd som är varken tidsavståndet
eller rumsavståndet (som du föreslår) eller Minkowskiavståndet. Jag behöver ett avstånd som växer
med rumsavståndet OCH tidsavståndet. Varför inte diskutera hur man kan använda ett sådant
avstånd?
Din definition av kovariant är ny för mig. För mig betyder kovariant "som transformeras som
enhetsvektorerna" men ett ord kan ju ha flera betydelser och nu vet jag vad du menar.
__________________
2012-12-16
Några synpunkter på dimensioner:
Tänk dig en helt tom rymd. Där finns inga punkter som kan urskiljas från omgivningen och därmed
inga riktningar och inga avstånd. Lägg in en störning i form av en urskiljbar punkt. Fortfarande får
du inga avstånd och inga riktningar. Du har en nolldimensionell värld. Lägg till en andra punkt. Du får
nu en endimensionell värld med en linje genom punkterna som definierar en riktning och avståndet
mellan punkterna kan användas som avståndsenhet. Lägg till en tredje punkt. Den kan ligga på linjen
och alltså ingå i den endimensionella världen men om den inte ligger på linjen definierar den en
tvådimensionell yta. Lägg till en fjärde punkt. Om den inte ligger i den tvådimensionella världen
definierar den en tredimensionell värld. På det viset kan du fortsätta. n+1 punkter kan alltså skapa
en n-dimensionell värld. Och i vårt universum finns det en hel del urskiljbara punkter. Men hur
många av dessa skapar egentligen en ny dimension?
I en endimensionell värld kan jag ange läge med en koordinat. I en tvådimensionell med två
koordinater och så vidare. Om jag har angett alla koordinater för två punkter befinner de sig på
samma plats om alla koordinater är lika och på olika platser om någon koordinat är olik. Om de
befinner sig på samma plats bör jag kunna upptäcka det genom att de växelverkar.
I min vardag upplever jag att om två föremål har samma latitud, samma longitud, samma höjd och
samma klockslag så växelverkar de alltid. Om någon av dessa koordinater är olik växelverkar de
aldrig. Min värld är alltså fyrdimensionell.
Min kunskap om strängteori är rudimentär. Det lilla jag har läst har inte gett någon mersmak. En
fyrdimensionell värld är tillräcklig för att jag skall kunna stoppa mat i munnen och undvika att
springa på hinder. Men visst kan det finnas behov att beskriva något annat men då vill jag ha en
begriplig motivering.
__________________
2012-12-18
Som jag ser det kan vi få längkontraktion och tidsdilation även i euklidisk metrik. Så frågan är
egentligen vad man utgår från. Om man ser vardagsmetriken som det enkla självklara är det
naturligt att utgå från den. Men visst kan man utgå från minkowskimetriken om man ser den som
det enkla och självklara.
Betrakta två system som rör sig i förhållande till varandra. Hur ser det ena systemet ut sett från det
andra?
Om det finns en högsta möjliga universell hastighet för information kommer denna att påverka
bilden. Bilden påverkas alltså inte bara av systemens hastighet i förhållande till varandra utan också
av den universella hastigheten.
Om man lägger tid som en koordinat vinkelrät mot rummet blir tidskoordinaten knuten till rummet
via den universella hastigheten.
Hastighet är tidsderivata. Om man deriverar med avseende på tidskoordinaten deriverar man alltså
med avseende på en koordinat som är knuten till rummet via den universella hastigheten. Lorentz
visade att man kan hantera detta med hjälp av Lorentztransformen.
Ett annat sätt är att dela upp tidsbegreppet i koordinattid och en universell parametertid. Man kan då
definiera hastighet som derivatan med avseende på parametertid, alltså på en
koordinatsystemoberoende förändringsparameter. Eftersom parametertiden inte har någon koppling
till den universella hastigheten blir detta enkelt och väldefinierat.
Genom att lägga in koordinattiden som en reell koordinataxel får begreppet "hastighet i
koordinattidsled" en innebörd. Det blir derivatan av koordinattiden med avseende på parametertiden.
Den universella hastigheten blir då min hastighet i koordinattidsled.
Jag kan då använda euklidisk metrik och ortogonala transformationer. Så vitt jag hittills funnit
fungerar detta. Men jag kan naturligtvis inte garantera att det alltid blir rätt.
En värld med reell koordinattid blir större än den gamla på samma sätt som en rymd är större än en
yta. Stora delar av den blir visserligen lika oåtkomliga som månen var på 1500-talet när man
började förstå var den fanns. Men om vi skall nå dit måste vi börja fundera på hur det skall gå till.
__________________
Inlägg av dbshw
*********************
Jag har en lada som är 50 meter lång, med öppningar i båda ändar. Pelle löptränar, och
bestämmer sig en dag för att springa genom denna lada så snabbt det går. Han springer i 0,99c.
Han har också ett stoppur, som han startar när han kommer in i ladan, och stoppar när han
kommer ut ur andra änden. Hur lång tid tar denna färd enligt stoppuret?
*********************
2012-12-20
Utmärkt. Det är med den här typen av exempel som man kan jämföra olika synsätt. Men det är inte
helt enkelt. Frågan är: "Om jag och Pelle har varsitt stoppur kommer de att visa olika värden när vi
jämför dem efteråt?". Men ett problem är att vi kan inte jämföra dem före och efter loppet utan att
Pelle och hans ur accelererar till och från 0.99c. Jag skall försöka bena ut det men jag behöver lite
betänketid.
Einstein försökte förklara vad tid var genom att säga att tid är det som en klocka mäter. Man kanske
kan anknyta till denna definition och säga att parametertiden är vad en klocka mäter och
koordinattiden är vad bilden av en klocka mäter.
Om jag står vid ladans ingångsdörr ser jag inte att Pelle har kommit fram vid den parametertid som
han trycker sitt stoppur vid. Jag måste vänta tills bilden av honom kommer fram till mig innan jag
trycker på mitt stoppur. Vid den parametertid när han är framme visar den bild av hans stoppur som
då når mig en kortare tid än mitt stoppur. Om jag kan se hans stoppur ser jag på det hur han rör sig
i min koordinattid. Mitt stoppur tickar på tills jag ser att han trycker på sitt. Då trycker jag på mitt
men på bilden där han trycker på sitt visar hans ur en kortare tid än mitt.
__________________
2012-12-21
Här kommer ett försök till beskrivning:
PELLES LADA
c är omräkningsfaktor mellan tidsenhet och längdenhet. Mäter jag tider i nanosekunder och längder i
fot blir c nära 1 fot/ns. Mäter jag tider i sekunder och längder i meter blir c = 3x10^8.
Att passera en 50 m lång lada med hastigheten 0,99c tar parametertiden 50/0,99c = 50,5/c. Men
hur ser det ut för mig och för Pelle?
Jag färdas genom en fyrdimensionell värld med fyra vinkelräta koordinataxlar. Jag har med mig ett
ur. Även om allt annat omkring mig ser ut att stå stilla kan jag på uret se att jag rör mig på något
sätt eftersom visarna rör sig. Jag väljer då en av världens koordinataxlar som min rörelseriktning
och kallar den axeln för koordinattidsaxel och de tre övriga axlarna för rumsaxlar. Det är alltså min
färdriktning genom världen som avgör vilken axel som blir koordinattid. I övrigt skiljer sig inte
koordinattiden från rummet.
Mitt ur visar att min värld förändras. Det mäter parametertiden och på urtavlan ser jag en bild som
visar att jag färdas framåt i koordinattidsriktningen.
När jag står vid ladans ingång ser jag en lada som skjuter ut 50 m i x-riktningen. Den ser ut att stå
stilla vilket innebär att den följer mig på min färd i koordinattidsriktningen.
Pelle har också ett ur. Det mäter också parametertiden och visar för honom att han färdas i sin
koordinattidsriktning. Men om jag tittar på hans ur ser jag att det inte visar samma som mitt.
Tydligen är hans koordinattidsrktning inte samma som min koordinattidsriktning. Hans
koordinatsystem är vridet vinkeln (a) så att sin(a) = 0,99. Det ger (a) = 82 grader.
När Pelle passerar ingången sammanfaller hans och mitt origo. Pelle ser då ladan men den ligger till
stor del i hans koordinattidsriktning. När han färdas i sin koordinattidsriktning kommer han alltså att
passera genom ladan. Och den skjuter inte ut 50 m i Pelles x-riktning utan bara 50 cos(a) = 7 m.
När jag tittar på Pelles klocka ser jag att den går saktare än min. När min klocka går 1 sekund går
Pelles klocka bara 0,14 sekunder. Hans färdriktning ligger ju till stor del i mitt rum. Han färdas bara
långsamt i min koordinattidsriktning.
Ladans längd i Pelles koordinattidsriktning alltså den parametertid som Pelle mäter när han passerar
ladan får jag genom att projicera ladan på Pelles koordinattidsaxel. Den blir 50/csin(a) = 50,5/c
sekunder. Och den parametertid som jag avläser och klockar på mitt stoppur blir 50,5/c0,14 = 360/c
sekunder.
360/c sekunder efter att Pelle sprang in i ladan ser jag alltså en bild där han kommer ut och trycker
på ett stoppur som visar 50,5/c sekunder.
Jag ser alltså en lång lada , en långsam Pelleklocka och en Pelle som springer med hastigheten
0,99c. Pelle ser en kort lada , en snabb Pelleklocka som visar parametertid och han upplever att han
springer 7 m med hastigheten 0,99cx0,14 vilket tar honom parametertiden 50,5/c sekunder.
__________________
2012-12-22
Kanske kan vi så småningom förstå varandra.
Vi använder olika definition av begreppet "hastighet". För mig är hastighet kvoten mellan
rumsförflyttning och parametertid medan du ser hastighet som kvoten mellan rumsförflyttning och
koordinattid. Det betyder att vi uppfattar begreppet "Pelles hastighet" på olika sätt.
Begreppen parametertid och koordinattid kommer från mitt sätt att se världen som en ändlig mängd
kvanta ordnade i fyra dimensioner. En händelse innebär en förändring och en kvantaförflyttning,
alltså en förändring och en rörelse. Jag har försökt beskriva detta i olika sammanhang men jag
klarar inte av att göra det här. Men ett sätt kanske är följande.
Om jag håller en klocka i handen mäter den parametertid och visar en koordinattid som direkt följer
parametertiden. När Pelle håller en klocka i handen mäter den parametertid och visar honom en
koordinattid som direkt följer parametertiden. Men när jag ser på Pelles klocka går den saktare än
min. Den visar alltså inte den parametertid som min klocka visar. Den visar hur Pelle färdas i min
koordinattid.
Jag försöker säga att om man ser parametertid och koordinattid som olika begrepp kan man
använda reell metrik. Men det förutsätter att man använder parametertid och koordinattid som
skilda begrepp.
Om du projicerar Pelles koordinatsystem på mitt koordinatsystem multiplicerar (eller dividerar) du
såväl längd som koordinattid med cosinus för vridningsvinkeln. Då blir kvoten mellan längd och
koordinattid oförändrad. Det du kallar hastighet blir alltså oförändrat. Men om man som jag gör ser
hastighet som kvoten mellan längd och parametertid multipliceras längd med cosinus för
vridningsvinkeln medan parametertiden blir densamma. Detta hastighetsbegrepp transformeras
alltså på samma sätt som längd. Det innebär att man inte bara kan säga att Pelle sprang med
hastigheten 0,99c, man måste tala om i vilket system han hade hastigheten 0,99c.
Man kan naturligtvis definiera hastighet som längd dividerad med koordinattid och säga att Pelle
sprang genom 7 m lada med 0,99c vilket alltså ger 7,1/c sekunder. Som jag ser det sprang han då i
mitt system genom 7/0,14 = 50 m lada på 7,1/0,14c sekunder vilket ger hastigheten 0,99c.
Jag föredrar definitionen längd per parametertid men visst kan man använda definitionen längd per
koordinattid bara man vet vad man gör. Att jag föredrar längd per parametertid beror bland annat
på att jag då får sin i stället för tan men jag vet inte om jag kan beskriva det utan att kunna rita.
__________________
2012-12-23
Jag färdas i min koordinattidsriktning genom min värld. Pelle färdas i sin koordinattidsriktning genom
min värld. Hans koordinattidsriktning bildar vinkel (a) med min. Vi startar båda i origo.
När parametertiden T gått har jag färdats sträckan T i min koordinattidsriktning och Pelle har färdats
sträckan T i sin koordinattidsriktning. Det innebär att Pelle har färdats Tsin(a) i min x-riktning (alltså
rumsriktning) och Tcos(a) i min koordinattidsriktning.
Om jag definierar hastighet som väg per parametertid blir Pelles hastighet Tsin(a)/T = sin(a). Om
jag definierar hastighet som väg per koordinattid blir Pelles hastighet Tsin(a)/Tcos(a) = tan(a). Vid
små vinklar är vinkeln, sin och tan ungefär lika och vid de hastigheter vi normalt rör oss med är det
svårt att skilja mellan dem. Men det kan finnas en känguru i sättet att definiera hastighet.
Detta synsätt har enorma konsekvenser när det gäller synen på tidsresor för om (a) överstiger 90
grader börjar Pelle springa bakåt i min koordinattid när parametertiden ökar. Koordinattiden går ju
liksom övriga riktningar både framåt och bakåt.
__________________
2012-12-25
PELLES LADA (forts)
Pelle mäter i lugn och ro ladan och finner att den är 50 m. Så sover han en stärkande sömn inför
morgondagens lopp. Han springer genom ladan med ett stoppur i handen. När han kommer ut och
trycker på stoppuret visar det 50,5/c. När han har bromsat in och lugnat ner sig säger han:
"Jag fixade det! Jag sprang 50 m på 50,5/c alltså med hastigheten 0,99c. Du såg också att stoppuret
visade 50,5c när jag kom ut och tryckte på det."
"Ja" säger jag "jag såg att ditt stoppur visade 50,5/c men jag såg också att det gick saktare än mitt.
Så jag klockade också loppet och när du kom ut visade mitt stoppur 362/c. Du sprang alltså bara
0,14c. Om du vill se det i ditt koordinatsystem sprang du 7 m på 50,5/c vilket också blir 0,14c. Jag
godkänner inte 0,99c."
"Jamen" säger Pelle "att ladan i mitt koordinatsystem bara är 7 m beror ju på att den är uppdelad i
en komposant i x´-led som är 7 m och en komposant i t'-led som är 0,99x50 = 49,5 m. Lägger jag
ihop dessa komposanter på rätt sätt blir ladan även i mitt system 50 m."
"Nej" säger jag "med ladans längd menas ladans längd i rummet, alltså för din del i x´-led det vill
säga 7 m. Du har långt kvar till 0,99c."
"Men" säger Pelle "om jag vrider mitt koordinatsystem ännu mer kommer min klocka att gå ännu
långsammare. Det här var på gränsen till vad jag klarade av så det är ingen ide att jag försöker.
Som jag ser det klarade jag uppgiften."
Pelle färdas med hastigheten 1c i sin koordinattidsriktning. Han projicerar ladan på sin
koordinattidsriktning genom att multiplicera med sinus för vridningsvinkeln. det blir 49,5 m. Han
springer 50,5 m i sin koordinattidsriktning vilket innebär att han håller på så länge att han färdas
50,5 m i sin koordinattidsriktning. Han projicerar sin färd i koordinattidsriktningen på ladan genom
att multiplicera med sinus för vridningsvinkeln. Det blir 50 m.
För att projicera ladan på sin koordinattid multiplicerar Pelle ladlängden (50 m) med sinus för
vridningsvinkeln. För att hitta en koordinattid som har projektionen 50 m på ladan dividerar Pelle
ladlängden (50 m) med sinus för vridningsvinkeln.
__________________
2012-12-27
Jag skall försöka ge en kort beskrivning av mitt sätt att se på min värld. Som jag ser det finns det
en del fördelar med det som gör att jag funnit det mödan värt att tillägna mig det. Därför berättar
jag gärna om det men det är inte det enda möjliga sättet att se och det står naturligtvis var och en
fritt att välja sitt synsätt. Men för att ett synsätt skall vara användbart måste det uppfylla kravet att
de fenomen som vi upplever beskrivs på ett sätt som överensstämmer med den bild som våra
sinnen ger oss.
Min världsbild bygger på följande antaganden:
Världen kan ses som en ändlig mängd kvanta inplacerade i en ändlig mängd kvantapositioner
ordnade i fyra dimensioner.
Ett kvanta kan bara byta plats med närliggande kvantaposition. En sådan kvantaförflyttning är
"minsta detekterbara händelse".
Jag ser en fyrdimansionell värld. För att ange läge för en punkt krävs fyra koordinater. Min bild av
världen förändras. För att ange förändring behöver jag en förändringsparameter. Jag kallar denna
för parametertid. Parametertiden är en skalar som inkrementeras varje gång en minsta detekterbar
händelse inträffar någon stans i världen.
Att min värld förändras innebär att jag färdas genom den. När parametertiden går ändras alltså mitt
läge i min värld. Jag kan lägga in ett fyraxligt ortogonalt koordinatsystem och vrida det så att en av
axlarna ligger i min färdriktning. Jag kallar den axeln för koordinattidsaxel. Den skiljer sig från mina
tre rumsaxler enbart genom att jag färdas längs den. Pelle kan färdas i en annan riktning och får då
en koordinattidsaxel som bildar vinkel med min och går genom det som jag kallar rum.
Min världsbild är alltså inte egocentrisk. Jag står inte stilla i origo. Jag färdas i
koordinattidsriktningen genom min värld.
Med "hastighet" menar jag förflyttning i koordinatsystemet i förhållande till förändringstakten alltså
lägesförändring dividerad med parametertid. Med "rumshastighet" menar jag förflyttning i rummet
dividerad med parametertid. Med "koordinattidshastighet" menar jag förflyttning i koordinattid
dividerad med parametertid. Jag färdas med hastigheten c i min koordinattidsriktning och Pelle
färdas med hastigheten c i sin koordinattidsriktning men om våra koordinattidsaxlar inte är parallella
kommer Pelle inte att färdas med hastigheten c i min koordinattidsriktning.
Jag ser "tid" som ett sammanfattningsbegrepp för parametertid OCH koordinattid.
För transformation mellan olika koordinatsystem, till exempel koordinatsystem med olika riktning på
koordinattidsaxeln, gäller vanliga transformationsregler för euklidiska system.
På denna världsbild projicerar jag den bild som mina sinnen ger mig av min värld. Jag kan alltid
projicera till en bild. Jag kan till exempel projicera Jordens klotyta till ett plant fotografi eller en plan
karta men projektionen blir inte bijektiv. Den blir ofullständig så att jag inte kan återskapa förlagan
från bilden. Frågan är då: Blir min bild fullständig? Beskriver den verkligheten så att jag kan
återskapa verkligheten från bilden?
Jag använder gängse projektionsregler, alltså att om jag vill ha projektionen C av vektorn A på
vektorn B multiplicerar jag beloppet för A med cos för vinkeln mellan A och B och får då C i B:s
riktning. Och om jag vet C och vinkeln mellan A och B dividerar jag beloppet av C med cos för
vinkeln för att få beloppet av A.
Överensstämmer detta med den värld vi observerar? Transformation mellan två system med olika
riktning på koordinattidsaxeln ger den vanliga längdkontraktionen och tidsdilationen. Men ger inte
definitionen av hastighet som sin i stället för tan för vridningsvinkeln olika resultat? En känguru??
Om jag definierar hastighet som sin blir lorentzkontraktionen cos som alltså blir noll vid 90 grader.
Men om jag definierar hastighet som tan blir lorentzkontraktionen noll redan vid 45 grader
(hyperbelns assymptot). En klar skillnad eller???
Frågan är hur jag bestämmer vridningsvinkeln. Om jag definierar hastighet som sin får jag
vridningsvinkeln som arcsin för hastigheten. Om jag definierar hastighet som tan får jag
vridningsvinkeln som arctan, alltså en mindre vinkel. Och båda synsätten ger lorentzkontraktionen
noll vid samma hastighet.
__________________
2012-12-27
Einstein definierade tid som "det som en klocka mäter".
Men vad är det som en klocka mäter? Klockan räknar förändringar hos det tidgivande elementet i
klockan. Om klockans tidsgivande element är en n:tedel av hela världen och det inträffar a
förändringar i klockans tidgivande element kan jag dra slutsatsen att det i hela världen har inträffat
axn förändringar. Klockan mäter alltså antalet förändringar i min värld, det vill säga parametertiden.
Om jag mäter hastighet genom att mäta förflyttning i mitt koordinatsystem och dividera med
klockans uppmätta tid har jag alltså mätt hastighet som förflyttning dividerat med parametertid.
__________________
2012-12-30
Det är säkert så att jag ibland uttrycker mig otydligt och slarvigt. Men jag försöker vara tydlig och
jag uppskattar påpekanden om otydligheter.
Så till frågan om sin eller tan.
Rita en t-axel och en vinkelrät x-axel. Det är mitt system. Rita in Pelles färdväg som en rät linje
genom tredje kvadranten, origo och första kvadranten. Pelles färdväg bildar vinkeln (a) med min t-
axel. I punkten (0,t) är beloppet av t parametertiden. Jag brukar beteckna parametertiden med tao
men här använder jag, något oegentligt, t både för parametertiden och för koordinaten i (0,t).
Rita en cirkel med t som radie. Rita en med x-axeln parallell linje från den punkt där cirkeln skär
Pelles färdväg och till t-axeln. Längden av denna linje blir t sin(a) och det är Pelles förflyttning i mitt
system. Linjen träffar t-axeln i (0,t cos(a)). t cos(a) är vad bilden av Pelles klocka visar när den når
mig.
Situationen när Pelle kommer ut ur ladan är alltså att han färdats t sin(a) i min x-riktning, att min
klocka visar t, att Pelles klocka för Pelle visar t och att den bild av Pelles klocka som når mig visar t
cos(a).
Frågan är nu: Vad menas med hastighet? Är det t sin(a) / t = sin(a) eller t sin(a) / t cos(a) = tan
(a)?
För små värden på (a) är (a), sin(a) och tan(a) ungefär lika. Vid de hastigheter vi normalt rör oss
med går det inte att se någon skillnad mellan sin(a) och tan(a).
Sätter jag hastigheten till sin(a) blir Lorentzkontraktionen cos(a). Sätter jag hastigheten till tan(a)
blir Lorentzkontraktionen (SQR(cos^2(a) - sin^2(a))) / cos(a). Här dyker alltså hyperbelns
minustecken upp. Det beror på att jag ersatt Pelles klocka med bilden av Pelles klocka. Det är därför
jag försöker påpeka att minkowskiavståndet inte är avstånd till en händelse utan avståndet till
händelsens bild.
__________________
2013-01-06
För femtio år sedan jobbade jag med radar och siktesberäkninger. Då måste man se världen från
åtminstone tre utgångspunkter: anfallarens, målets och markkontrollens. Det blir tre bilder som ser
olika ut men eftersom de alla avbildar samma verklighet kan de transformeras i varandra. I
anfallarens bild ser det ut att vara självklart att man styr rakt mot målet. I markkontrollens bild ser
man att det blir en hundkurva alltså den väg en hund springer mot bytet utan att förstå att det går
att genskjuta bytet. I ett direktanfallssikte styr man i stället så att man håller konstant syftvinkel till
målet.
När man skall beräkna avfyringstidpunkt kan man använda en sorts minkowkimetrik där man sätter c
lika med projektilhastigheten. Projektilen är ju en sorts "bild" av skytten.
Vackert eller fult? Som jag ser det är minkowskimetriken elegant. Till och med bländande elegant
och i vissa sammanhang är det lämpligt att använda den. Men den är så bländande att den fått
överglänsa och dölja de möjligheter som man kan se med andra synsätt. Jag håller helt med om att
man skall se det vackra men det kan finnas vackra möjligheter även i mindre vackra omgivningar.
Det kan vara mödan värt att leta även där.
När det gäller tidsbegreppet ser jag det som ett sammanfattande begrepp för begreppen
parametertid och koordinattid. Det gör att definitionen av hastighet som väg genom tid inte blir
entydig. Man måste bestämma sig för om hastighet är väg genom parametertid eller väg genom
koordinattid. Vid de hastigheter vi normalt hanterar blir skillnaden inte märkbar men när man
närmar sig ljushastighet blir den tydlig.
Jag har försökt påpeka att tidsdilationen och längdkontraktionen inte enbart hänger samman med
minkowskimetriken. Även en vridning av ett fyrdimensionellt reellt koordinatsystem ger tidsdilation
och längdkontraktion.
__________________
2013-01-08
Då får vi se om jag kan uttrycka mig begripligt.
Pelle, Kalle och jag färdas i våra koordinattidsriktningar. När parametertiden går en tidsenhet
förflyttar vi oss 1 tidsenhet = c längdenheter i vår koordinattidsriktning. Kalle och jag har samma
riktning på vår koordinattid. När parametertiden går T tidsenheter förflyttar kalle och jag oss T
tidsenheter = Tc längdenheter i vår koordinattid. Men Pelles koordinattid bildar vinkeln (a) med min
koordinattid. När parametertiden går T tidsenheter förflyttar Pelle sig T tidsenheter i sin
koordinattidsriktning. Men det innebär att han förflyttar sig T sin(a) tidsenheter = Tc sin(a)
längdenheter i min x-riktning och T cos(a) tidsenheter = Tc cos(a) längdenheter i min
koordinattidsriktning. Pelle färdas alltså saktare i min koordinattidsriktning än vad Kalle och jag gör.
Pelle har fått uppgiften att springa genom ladan med hastigheten 0,99c. Han tolkar det som att han
skall springa genom den 50 m långa ladan på tiden 50/0,99c = 50,5/c. Dagen innan har han mätt
upp ladan och konstaterat att den är 50 m. Han tar med sig ett stoppur och en meterstav. Med
meterstaven kontrollerar han att ladan fortfarande är 50 m och han springer så att stoppuret visar
50,5/c när han kommer ut ur ladan.
Eftersom bortändan på ladan befinner sig på avstånd i mitt rum kan jag inte säkert avgöra när Pelle
kommer ut ur ladan. Och eftersom ingången befinner sig på rumsavstånd från Kalle kan Kalle inte
säkert avgöra när Pelle springer in i ladan.
I mitt koordinatsystem sprang Pelle (50,5/c)c sin(a) = 50 längdenheter i x-riktningen och han
flyttade sig då (50,5/c) cos(a) tidsenheter i min koordinattidsriktning. Det ger att sin(a) = 0,99 och
cos(a) = 0,14. Han flyttade sig alltså 7,07/c tidsenheter i min koordinattidsriktning.
Jag projicerar ladans längd på Pelles x-axel och finner att den blir 7 m.
När Pelle kommer ut ur ladan skickar Kalle en signal. När Kalles signal når mig drar jag bort
rumsavståndet och finner att Pelle hade bara flyttat sig (50,5/c) 0,14 = 7,07/c tidsenheter i min
koordinattidsriktning när han kom ut ur ladan.
Vid morgonfikat nästa dag träffas vi och diskuterar resultatet.
"Jag klarade uppgiften" säger Pelle "Jag sprang 50 m på 50,5/c tidsenheter. Det innebär att jag
sprang med hastigheten 50/(50,5/c) = 0,99c".
"Nja" säger Kalle "Du sprang på tok för fort. Du sprang 50 m på 7,07/c tidsenheter. Du sparng med
hastigheten 50/(7,07/c) = 7,07c ".
"Nej" säger jag "Du sprang bara 7 m på 50,5/c tidsenheter. Att du mätte längden till 50 m när du
sprang beror på att du mätte med en meterstav som hade krympt.Du sprang med hastigheten 7/
(50,5/c) = 0,14c".
"I så fall" säger Pelle " sprang jag 7 m på 7.07/c tidsenheter vilket blir hastigheten 0,99c. Så jag
klarade uppgiften".
Vem har rätt? Svaret är att det beror på vad man skall ha resultatet till.
När byborna som rodde klockan över sjön får frågan: "Var tappade ni klockan?" kan de visa på
märket i båtkanten. Om det är rätt eller fel svar beror på vem som frågade. Är det en båtbyggare
som skall bygga en ny båt där det är mindre risk att tappa klockan är svaret rätt. Är det en dykare
som skall leta efter klockan är det fel.
Så en liten invändning mot uttrycket "din teori". Jag försöker bara påpeka att man naturligtvis kan
avbilda världen på många olika sätt och antyda ett sätt som jag brukar använda.
__________________
2013-01-11
Ett problem med beskrivningen av Pelles lada är vad som menas med "...drar jag bort
rumsavståndet...". Det är långt ifrån självklart vad detta innebär. Jag skall, mycket kort, försöka
antyda ett problem med minkowskimetrikens sätt att hantera detta.
Einstein och Minkowski sa i princip: "Jag kan inte veta något om en händelse förrän dess bild når
mig. För mig inträffar händelsen när bilden når mig. Jag kan då ersätta händelsen med händelsens
bild och sätta avståndet till noll när bilden når mig. Det innebär att jag kan använda ett
avståndsbegrepp som blir noll när tidsavståndet är lika med rumsavståndet."
I ett växelströmsnät kan man ansluta synkronur som följer nätets fasläge. Jag vet inte var vårt näts
tidgivare ligger idag men jag har för mig att den en gång i tiden låg vid Harsprånget. Följer man
kraftledningen därifrån förskjuts fasläget så att alla synkronur som är inkopplade på nätet får
minkowskiavståndet noll. Man kan säga att klockorna går minkowskisynkront. En klocka i Smygehuk
går då dt sekunder efter klockan i Harsprånget.
I många fall fungerar detta problemfritt. Innevånarna i Smygehuk märker inte att deras klocka går
efter Harsprångetklockan. Och ett lokalt litet kraftverk i Smygehuk kan fasa in sig på nätet och
leverera el till den närmaste omgivningen utan att det blir några problem.
Men vad händer om jag tar med mig ett atomur till Harsprånget, ställer det efter
Harsprångetklockan och tar med det till Smygehuk? Visar atomuret och den synkrona klockan olika
tid när jag kommer till Smygehuk? Om de visar olika är det då atomuret eller den synkrona klockan
som visar rätt tid i Smygehuk?
Om jag bygger en kraftledning från Harsprånget till Moskva och sedan fortsätter till Tyskland och
Danmark och därifrån till Smygehuk kan jag ha två synkrona klockor i Smygehuk en som visar
fasläöget för direktledningen och en som visar fasläget på Moskavledningen. Två klockor med
minkowskiavståndet noll som vid samma tid och plats visar olika tid. Och kopplar man ihop
direktledningen med Moskvaledningen kan man få en intressant demonstration av problemet med att
lita på minkowskimetriken.
__________________
2013-01-12
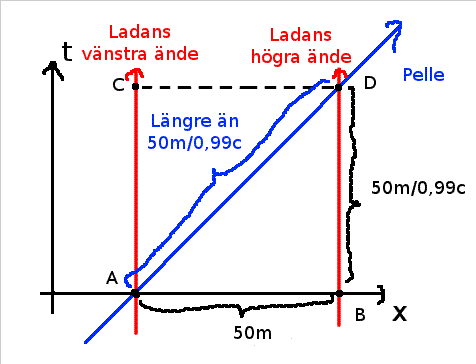 Vi försöker igen.
Jag använder din figur. Som jag ser det är den blå linjen Pelles t-axel. Längden i den blå riktningen
är alltså vad Pelles stoppur visar för Pelle. Han springer nu så att den blå sträckan som du angett
som "längre än 50 m/0,99c" blir 50/0,99c. Den röda sträckan som du angett som "50 m/0,99c" är
min tolkning av Kalles signal vilken alltså är mindre än 50/0,99c. Genom att Pelle delvis springer i
mitt rum rör han sig långsammare i min koordinattidsriktning (t-riktning).
Minkowskimetriken bygger på tanken att det finns ett tidsavstånd som kan uppväga ett rumsavstånd
så att resultatet blir noll. Om tidsavståndet är lika med rumsavståndet blir Minkowskiavståndet noll.
Detta fungerar i många fall eftersom vi upplever bilden av en händelse som om den var händelsen.
Vi är tydligen överens om att två punkter med Minkowskiavståndet noll kan ha ett reellt avstånd.
Som jag ser det betyder det att man även måste hålla reda på det reella avståndet vilket
Minkowskimetriken inte gör. Som jag ser det kan Minkowskimetriken komplettera den reella
metriken men inte ersätta den.
__________________
2013-01-14
Om jag ser en stjärna explodera säger jag: "Nu exploderade stjärnan."
Så tänker jag efter och ändrar det till: "Nu blev minkowskiavståndet till stjärnexplosionen noll. Hur
skall jag lägga in det i mitt koordinatsystem?"
Om stjärnan ligger en miljon ljusår bort och om det hade funnits en enorm klocka på stjärnan som
jag kunde se skulle jag se att klockan visade en tidpunkt för en miljon år sedan. Jag ritar då ett
koordinatsystem med en t-axel och en x-axel och med mig i origo. Så lägger jag in
stjärnexplosionen vid t lika med minus en miljon år och x lika med en miljon ljusår.
Stjärnexplosionens koordinattid i mitt system blir alltså minus en miljon år. Sedan dess har
parametertiden gått och jag ha färdats längs min t-axel så att jag nu kommit till origo. Och bilden av
stjärnexplosionen har färdats längs min x-axel så att den nu nått origo där jag kan se den. Från
origo är avståndet i t-riktningen lika stort som avståndet i x-riktningen vilket innebär att
minkowskiavståndet är noll.
Jag tror att detta är ett mycket vanligt sätt att se situationen.
__________________
2013-01-15
Det är mycket möjligt att man inte behöver något annat avståndsbegrepp i relativitetsteori. Men
relativitetsteori är inte hela världen. Den har funnits i cirka hundra år men den reella metriken har vi
använt i många tusen år. Jag tar inte ett steg utan en mängd avståndsbedömningar till väggar. golv.
möbler med mera.
Du har sagt någon gång att man kan bortse från relativitetsteori i vardagen. Att man alltså kan se
relativitetsteori som en spekulation fristående från vardagens verklighet. Så var det kanske för
hundra år sedan men det har hänt en del sedan dess. Vi möter idag en hel del fenomen där
ljushastigheten spelar en viktig roll.
Hela radartekniken bygger på att rumsavståndet är lika med tidsavståndet när minkowskiavståndet
är noll. I GPS använder vi skillnader i koordinattid mellan reellt synkrona klockor placerade i sateliter
med kända lägen. Vi bygger allt större växelströmsnät med mimkowskisynkronism. När jag bygger
ett kretskort för att hantera datorpulser måste jag tänka på att en nanosekundpuls inte är längre än
en fot. När jag ringer till Australien får jag ibland en fördröjning som kräver en viss samtalsdisiplin.
Vi är på väg mot rymdfärder över avstånd där skillnaden mellan parametertid och koordinattid
spelar stor roll.
Allt oftare dyker de samband som ursprungligen härleddes via relativitetsteori upp i andra
sammanhang och med annan härledning. Som jag ser det är det viktigt att ha någon uppfattning om
hur olika synsätt hänger samman.
Minkowskimetriken är inte en egenskap hos verkligheten. Den är en transform som skapats via en
transformationsregel. När jag fotograferade med negativ färgfilm fick jag en en bild där färgerna
transformerats via en transformationsregel. Men eftersom denna regel var bijektiv kunde man vända
på regeln och kopiera bilderna tillbaka till förlagans färger. På samma sätt transformerar man till
minkowskimetriken via en transformationsregel. Men genom att man låser ett samband mellan
tidsavstånd och rumsavstånd blir denna transform inte bijektiv. Det går alltså inte att från
minkowskimetrikens bild bestämma reella avstånd. Minkowskimetriken kan därför bara komplettera
den reella metriken, inte ersätta den.
Det är inte något fel i att använda transformer. Laplace-transformer är mycket användbara inom
reglerteknik, Fourier-transformer är utmärkta när man bygger förstärkare och minkowskimetriken
har ett klart tillämpningsområde. Men en transform är aldrig det enda möjliga synsättet.
Det finns en egendomlig inställning att alla måste se allt på samma sätt. Så är det inte. Det är
genom att vi ser saker på olika sätt som vi kan hitta nya möjligheter. Men då behöver vi tala om för
varandra vad vi ser och naturligtvis måste vi vara öppna för att anpassa vårt synsätt så att det
stämmer med de fenomen som vi observerar.
__________________
2013-01-17
Det reella avståndet till en händelse är roten ur (x^2+y^2+z^2+tc^2).
En händelse kan orsaka en bild som med hastigheten c utbreder sig i alla riktningar. Avståndet till
händelsens bild ärroten ur ( x^2+y^2+z^2-tc^2). Minkowskiavståndet till en händelse är alltså
avståndet till händelsens bild. Eftersom mottagandet av händelsens bild är mitt enda sätt att få veta
något om händelsen kan jag i många fall ersätta händelsen med händelsens bild.
Världen påverkas inte av mitt sätt att avbilda den. Jag kan välja om jag vill avbilda på ett
koordinatsystem med raka eller krokiga, reella eller imaginära axlar. En bild av världen avbildar även
alla fenomen som vi observerat. Det kan vara lämpligt att välja en avbildning som ger en lättanvänd
beskrivning av världen inklusive dess fenomen. Även om jag inte lyckats beskriva det tillräckligt
tydligt har jag försökt tala om att jag använder ett fyrdimensionellt koordinatsystem med raka
ortogonala reella axlar. Om jag i detta beskriver rumshastighet som en vridning av
koordinattidsaxeln så att rumshastigheten blir lika med c gånger sinus för vridningsvinkeln får jag
enkla uttryck för längdkontraktionen och tidsdilationen.
Varje gång en detekterbar händelse inträffar någon stans i universum förändras det och
parametertiden inkrementeras. Parametertid är alltså antalet minsta detekterbara händelser i
universum. Ett antal är en skalär storhet. Varje förändring av universum innebär att mitt läge i
förhållande till mitt omgivande universum förändras. Det lägger jag in i mitt koordinatsystem som att
jag flyttar mig en tidsenhet lika med c längdenheter längs min koordinattidsaxel när parametertiden
ökar med en tidsenhet.
En klocka räknar antalet händelser i ett tidsgivande element. Eftersom det tidsgivande elementet är
en viss andel av hela universum blir detta ett mått på antalet händelser i hela universum. En klocka
mäter alltså parametertid.
Om det vid en händelse finns en klocka kommer bilden av klockan att följa med händelsens bild.
Denna bild av klockan visar då händelsens koordinattid i mitt koordinatsystem.
__________________
2013-01-21
Som jag ser det visar MM:s försök ingenting annat än att Jorden (och mätanordningen) ligger stilla i
förhållande till den eter som den svävar i. Av detta kan man varken dra slutsatsen att
ljushastigheten alltid är konstant eller att ljusstrålar alltid är raka. Det finns mycket att säga om
detta och jag funderar på om jag kan åstadkomma en begriplig sammanfattning.
När jag läste om relativitetsteori gjorde man ett stort nummer av att man kan inte veta något om en
händelse förrän man nås av händelsens bild. Man hävdade att det innebär att man kan ersätta
händelsen med händelsens bild. Avståndet till händelsens bild kan man skriva som roten ur (x^2+y^
2+z^2-tc^2). Men argumentet håller inte. Bilden av en händelse är något annat än händelsen.
Om jag kör in i en blockerad vägkorsning växelverkar jag med händelsen "blockerad korsning".
Resultatet blir en händelse som kallas "krock". Om jag bromsar in när jag nås av bilden av
"blockerad korsning" växelverkar jag med bilden av "blockerad korsning". När korsningen blir fri kan
jag köra igenom rumskoordinaterna för "blockerad korsning" men eftersom tidskoordinaten då blir
en annan får jag ingen växelverkan med "blockerad korsning".
Som jag ser det kan man använda Minkowskimetrik för händelsers bilder. Det är inget fel i det. Det
kan i många fall vara ett användbart sätt att hantera problem. Men det ersätter inte behovet av att
hantera händelser.
__________________
2013-01-22
Som ett plankton svävar i en havsström svävar jag i en eter som blåser med ljushatighet i en
riktning som jag kallar koordinattidsriktningen. Föremål i min omgivning svävar i samma eter och ser
ut att stå stilla. Men etervindens riktning är inte alltid exakt densamma. Om den avviker vid ett
föremål ser jag det som att föremålet rör sig i förhållande till mig.
När jag kör med min bil vrider jag min koordinattidsaxel så att den bildar en vinkel med markens
koordinattidsruktning. Jag ändrar alltså etervindens riktning kring bilen. På samma sätt som luften i
kupen följer med bilen följer etern kring bilen med bilen. En MM-mätare i bilen kommer alltså att
visa att bilen ligger stilla i förhållande till etern i bilen liksom en MM-mätare på marken visar att
marken ligger stilla i förhållande till etern vid marken.
Jag kan inte komma från marken till bilen utan att accelerera. Mellan bilen och marken finns alltså
ett accelerationsskikt det vill säga ett gravitationsfält. Ljusstrålar kröks i ett gravitationsfält. När jag
tittar ut genom vindrutan på bilen ser jag alltså ljusstrålar som krökts i ett gravitationsfält.
När jag tittar ner i vattnet händer det att jag ser en fisk. Om jag med ett spjut hugger mot bilden av
fisken bommar jag. Ljusstrålarna kröks vid vattenytan så att bilden av fisken inte sammanfaller med
fisken. SR är ett sätt att hantera detta genom att flytta fisken till bilden så att man kan använda raka
ljusstrålar. En annan möjlighet är att räkna med krökta ljusstrålar som flyttar bilden till fisken.
När jag tittar ut genom vindrutan blir ljuskrökningen så liten att den inte spelar någon roll. Och för
hundra år sedan var det knappast något annat än en vetenskaplig spekulation. Men om jag till
exempel jobbar med tröghetsnavigering använder jag gravitationsfältspassagerna för att bestämma
hastighet så att jag med hjälp av hastighet och en klocka kan bestämma läge. Här spelar även
obetydliga gravitationsfält vid färdens början en stor roll.
Jag har aldrig funderat på om begreppet "händelsens bild" är vanligt. Bara på om det är begripligt
och det tror jag att det är.
__________________
2013-01-26
För att hantera min värld behöver jag en bild där jag kan lägga in ett koordinatsystem så att jag får
koordinater som jag kan räkna med. Om jag gör en bijektiv avbildning innehåller bilden all
information om världen. Det går då att från bilden återskapa världen och alla bildens egenskaper
kommer från världen. Om jag förenklar bilden genom att avbilda flera punkter på samma bildpunkt
blir min avbildning inte bijektiv. Min bild kommer då att innehålla dels egenskaper som kommer från
världen, dels egenskaper som kommer från avbildningsfel.
1872 lade Felix Klein fram det så kallade Erlangenprogrammet där avbildningar indelas i klasser
efter vad som är invariant vid transformationer. Minkowskiavbildning och reell avblidning har olika
invarianter och tillhör alltså olika klasser. Men om avbildningen är bijektiv ger den, oberoende av
klass, en fullständig bild som enbart innehåller verklighetens egenskaper. En beskrivning av ett
fenomen i den ena avbildningen har då sin motsvarighet i en beskrivning i den andra avbildningen.
Vår reella avbildning är ett självklart inslag i vårt medfödda och vårt inlärda beteende.
Relativitetsteorin medförde att man såg en del samband som man inte tidigare hade sett. Men det
innebär naturligtvis inte att man bara kan avbilda världen på ett enda sätt. En bijektiv avbildning
enligt Minkowski och en bijektiv reell avbildning måste beskriva fenomen på sätt som ger samma
försöksresultat. Världen bryr sig naturligtvis inte om vilken avbildningsklass jag valt att använda.
En tredimensionell reell avbildning är inte bijektiv. När jag projicerar en fyrdimensionell värld på en
tredimensionell bild får jag samma typ av projektionsfel som när jag projicerar en klotyta på ett plan
(jag tycker trots allt att liknelsen ger en uppfattning av problemet). Minkowskiavbildningen är
fyrdimensionell och om den är bijektiv måste det gå att göra en bijektiv reell avbildning. Allt som kan
beskrivas i den ena avbildningen har då sin motsvarighet i den andra.
Som jag ser det blir det då intressant att ställa frågan: "Hur gör jag en reell avbildning som visar
motsvarigheten till de samband som relativitetsteorin påvisade?".
Man kan naturligtvis invända att de samband som man påvisade inom relativitetsteorin nu är
välkända och inte behöver någon annan beskrivning men jag tror att en bra reell beskrivning kan
visa oss nya oväntade samband. Och det skulle ha fördelen att vi kan betrakta världen utan att
behöva fundera på vilken avbildningsklass vi skall välja. Och jag tror att det är intressant oberoende
av om man kallar det fysik eller vardagshantering eller något annat.
__________________
2013-01-27
Visst ger olika avbildningar olika bilder där samband ser olika ut. Det är ju det som är poängen med
att använda olika avbildningar. Och du har rätt i att det kan hända att några samband som blir enkla
i Minkowskis avbildning bli svårhanterliga i andra avbildningar. Har du något bra exempel på de
symmetrier du pratar om? Något som är baserat på odiskutabla mätningar.
I många tusen år har vi använt reell avbildning. Vi har sett samband som vi betraktar som så
självklara att vi inte längre ser dem. Det är inte så att vi bara projicerar på ett tredimensionellt rum
genom att sätta dt=0. Vi är mycket medvetna om tidskoordinaten även om vi inte alltid formulerar
detta. Vi stoppar mat i munnen utan att med formler beskriva hur det går till.
För drygt hundra år sedan provade vi att använda Minkowskis avbildning och upptäckte att den
visade några samband som vi inte sett tidigare. Det var ju intressant men det betydde naturligtvis
inte att vi funnit den enda rätta avbildningen. Fortfarande lever många människor hela sitt liv med
daglig användning av reell avbildning men utan att ägna en tanke åt Minkowskis avbildning.
Jag vet inte varför du återkommer till att ljushastigheten skall vara konstant. I den värld jag ser är
den inte det. Jag ser c som min hastighet i koordinattidsriktningen, alltså som omräkningsfaktor
mellan längdenheter och tidsenheter.
Och en liten detalj. Om jag projicerar ett klot på ett plan blir väl projektionen RÄTT i en punkt. Och
om jag avbildar ett tredimensionellt klot på ett tvådimensionell plan tar jag väl bort en dimension.
Det spelar ingen roll eftersom det bara handlar om en liknelse men jag undrade vad du menar.
__________________
2013-01-28
Längdkontraktionen och tidsdilationen är ju väldokumenterade fenomen så låt oss börja med det.
Då är vi tillbaka i Pelles lada. Förra gången tyckte du att jag uttryckte mig otydligt så jag tänker ta
det bitvis så får vi se om det blir begripligt.
Först en viktig skillnad mellan SO(3,1) och SO(4).
I SO(3,1) är en koordinataxel speciell. Tid är något annat än längd och man kan direkt på
koordinatsystemet se vilken axel som är tidsaxel. Men om det finns en ändlig hastighet för
informationsöverföring blir längd och tid beroende av varandra. Detta beroende lägger du i
invarianten. Genom att använda en icke-ortogonal transform får du en koppling mellan
tidskoordinater och längdkoordinater. Det är ju det som är tricket med lorentztransformen.
I SO(4) är alla koordinater av samma typ. Jag kan inte, bara genom att se på koordinatsystemet,
avgöra vilken axel som är tidsaxel. Jag måste skilja mellan rum och tid på något annat sätt. När jag
ser på en klocka ser jag att den visar allt högre värden. Om jag avsätter klockslag och årtal på en
koordinataxel får jag alltså värden som ständigt ökar. Jag färdas alltså längs denna koordinataxel. I
SO(4) kan jag vrida mitt koordinatsystem så att bara en av mina fyra koordinater ökar. Jag kan
alltså lägga en koordinataxel i min färdriktning. Jag kallar den koordinataxeln för koordinattidsaxel.
Pelle gör likadant men det är inte säkert att han färdas i samma riktning som jag och det är alltså
inte säkert att hans koordinattidsaxel blir parallell med min. Det som för mig är rum kan vara tid för
Pelle och tvärtom. Den koppling mellan tid och rum som du i SO(3,1) beskriver med hjälp av en icke-
ortogonal transform beskriver jag i SO(4) som en vridning av koordinattiden.
Under min livstid kommer jag bara att passera de punkter som ligger på min koordinattidsaxel. Om
jag inte går in i ladan ligger den i mitt rum och sträcker sig i koordinattid utefter min
koordinattidsaxel utan att min koordinattidsaxel går in i ladan. Jag kommer alltså inte att passera
genom ladan. För att Pelle skall kunna ta sig igenom ladan måste han vrida sin koordinattidsaxel så
att den går genom ladan. Pelle och jag får alltså icke-parallella tidsaxlar.
Är vi överens om att man kan göra så? Om att detta sätt att se på världen inte strider mot några
kända regler?
_________________
2013-01-29
Om det finns en högsta möjliga hastighet c kan jag använda denna för att omvandla mellan
tidsenheter och längdenheter. c har egentligen inte med ljushastighet att göra annat än att
ljushastigheten i en viss situation är den högsta hastighet vi funnit. Jag jobbade en gång i tiden med
hjälpmedel för blinda bland annat frågan om hur man skapar en avståndsuppfattning utan hjälp av
synen. Här kan man använda ljudhastigheten som c. Men det viktiga är att c är en ändlig konstant.
När jag graderar min koordinattidsaxel tar jag en klocka. När klockan (parametertiden) går en
tidsenhet avsätter jag en tidsenhet, det vill säga c längdenheter, på min koordinattidsaxel
(koordinattid). Jag färdas alltså en tidsenhet, det vill säga c längdenheter, i koordinattidsriktningen
när paramertiden går en tidsenhet.
Jag kan dividera rumshastigheten v med c. Eftersom c är största möjliga hastighet kommer v/c att
ligga mellan -1 och 1. En storhet som ligger mellan -1 och 1 kan jag skriva som sin(a). Detta är ett
ganska vanligt sätt att hantera sådana storheter. Om jag sätter v/c = sin(a) blir lorentzkontraktionen
cos(a).
Jag återkommer till användningen av (a) men först är frågan: "Kan jag göra så här?" Har jag gjort
något som strider mot kända regler?
__________________
2013-01-30
Om jag anger en punkts läge med fyra av varandra oberoende (ortogonala) koordinater blir
lägesangivelsen fullständig. Om jag kastar en sten mot ett byte och alla stenens fyra koordinater
överensstämmer med bytets motsvarande koordinater träffar jag alltid. Så länge någon av stenens
koordinater avviker från bytets motsvarande koordinat träffar jag aldrig. En avbildning på ett
fyrdimensionellt ortogonalt koordinatsystem är alltså bijektiv.
Såväl en avbildning på SO(3,1) som en avbildning på SO(4) är bijektiv. Båda ger alltså en fullständig
beskrivning av verkligheten som innebär att verkligheten kan återskapas från beskrivningen. Världen
bryr sig inte om om jag använder ett koordinatsystem med fyra likadana axlar eller ett
koordinatsystem där jag särbehandlar en axel. Men avbildningarna blir olika och jag kan inte
använda samband från SO(3,1) i SO(4). Däremot måste naturligtvis utfallet av försök bli samma
oavsett om jag använt en beskrivning i SO(3,1) eller SO(4).
Om ljushastigheten är densamma i alla riktningar blir ljusstrålar raka. För att en ljusstråle skall
krökas måste ljushastigheten vara lägre längs innerkurvan än längs ytterkurvan. MM:s försök visade
att ljushastigheten INOM ett referenssystem är lika i alla riktningar. Av det kan man inte dra några
slutsatser som handlar om övergångar mellan referenssystem.
Jag kan inte komma från ett referenssystem till ett annat utan acceleration. Mellan två
referenssystem finns alltså ett accelerationsfält alltså ett gravitationsfält. Stjärnan vid
solförmörkelsen visar att ljuset böjs i solens gravitationsfält. Eftersom den enda kunskap vi har om
vad som finns på avstånd kommer från ljus och liknande fenomen som når oss ser vi inte om
ljusstrålar är raka eller krokiga. I en prismakikare är en ljusstråle långt ifrån rak men när vi tittar i
kikaren märker vi ingenting av dessa krokar.
Med raka ljusstrålar kan man bara se rakt. En ljusstråle längs x-axeln visar enbart vad som händer
på x-axeln. Man kan inte set runt ett hörn. Men en krokig ljusstråle kan ha varit inne i en annan
dimension. Om ljusstrålar kan vara krokiga kan det längs x-axeln komma en stråle som visar vad
som hänt på t-axeln. x-koordinaterna blir då inte helt oberoende av t-koordinaterna.
Hur skall man hantera att ljusstrålar böjs vid övergången mellan två referenssystem?
En möjlighet är att med en icke-ortogonal transform vrida rummet så att tidsaxeln får en
rumsprojektion. Man kan då använda koordinatsystem som särbehandlar tidskoordinaten SO(3,1).
En annan är att vrida hela koordinatsystemet. Då ändras vad som är tid och vad som är rum vilket
kräver att alla axlar betraktas som likvärda och utbytbara SO(4).
Relativitetsteorin beskriver ett sätt att transformera mellan SO(3,1)-system på sådant sätt att
ljusstrålar beskrivs som raka. Det betyder naturligtvis inte att de ÄR raka. Begreppen rak och krokig
hör till vår beskrivning av världen. Det är först när vi beskriver en ljusstråle som vi kan tala om rak
eller krokig.
Världen kan beskrivas i SO(3,1) eller SO(4) (och på andra sätt). Men beskrivningen blir olika och
man kan inte utan vidare ta samband från en beskrivning i SO(3,1) och använda dem i SO(4). Varje
beskrivning måste bygga på sina egna regler och övergång mellan beskrivningarna måste göras
med hjälp av regelövergångar.
__________________
2013-01-31
Då var det dags för längdkontraktion och tidsdilation i SO(4).
När Pelle springer genom ladan skall han se en kortare lada och jag skall se en Pelle som färdas
långsammare än jag i min koordinattidsriktning. Blir det så?
Sätt v/c till sin(a) och tolka (a) som vinkeln mellan min och Pelles koordinattidsaxlar. Då blir
lorentzkontraktionen cos(a). Och vinkeln mellan min och Pelles x-axel blir också (a). I Pelles system
får ladan en komposant i x-led och en komposant i t-led. x-komposanten blir ladans längd gånger
cos(a) (längdkontraktion) och t-komposanten blir ladans längd gånger sin(a).
När jag färdas T enheter längs min koordinattidsaxel färdas Pelle T enheter längs sin
koordinattidsaxel. Men eftersom Pelle delvis färdas i mitt rum, alltså i min x-riktning, kommer han att
färdas långsammare i min koordinattidsriktning. Han färdas bara Tcos(a) i min koordinattidsriktning
(tidsdilation) och i min x-riktning färdas han Tsin(a).
__________________
2013-02-01
Jag är naturligtvis medveten om att du kan ha rätt. Men om jag skall felförklara den avbildning som
människor använt i tusentals år och funnit användbar och pålitlig vill jag ha mycket påtagliga bevis.
Att man kan använda en annan avbildning är inte något bevis på att den gamla är fel Men - visst.
Jag tänker ibland på vilka konsekvenser det skulle ha men först vill jag veta hur jag kan använda den
gamla vanliga avbildningen.
Det är uppenbart att vi använder begreppet tid på sätt som vi inte kan använda rumskoordinater.
Som jag ser det beror det på att vi använder tid som ett sammanfattningsbegrepp för två olika
begrepp, parametertid och koordinattid. Parametertid är en skalär förändringsparameter,
koordinattiden är en koordinat av samma typ som rumskoordinaterna.
Om c är högsta möjliga hatighet och jag färdas med hastigheten c i koordinattidsled kan jag ju inte
röra mig fritt i koordinattidsled. Men det finns mycket att säga om detta. Jag skall försöka
återkomma.
Så vitt jag kunnat finna handlar alla MM-mätningar om mätningar inom ett referenssystem. Inga
delar av mätanordningarna rör sig i förhållande till varandra med hastigheter som närmar sig
ljushastighet. Då säger inte mätningarna något om övergångar mellan referenssystem.
Maxwells ekvationer säger inte alls att ljushastigheten är densamma i alla referenssystem. De säger
att ljushastigheten är ett genom roten ur produkten av det ljusbärande mediets
dielektricitetskonstant och magnetiska permeabilitet. Det är till exempel väl känt att ljushastigheten i
glas är lägre än i luft. Det är grunden för hela optiken. Och det handlar inte om att ljuset "studsar"
sig genom glaset. Vi kan mäta dielektricitetskonstant och magnetisk permeabilitet med metoder som
inte använder ljus och se att resultatet stämmer.
__________________
2013-02-01
Om avståndet mellan två punkter i euklidisk metrik är noll sammanfaller punkterna. Det är i så fall
en dubbelräkning av samma punkt. Det är ju detta som är innebörden i att avbildningen är bijektiv.
Man lägger aldrig två olika punkter med avståndet noll. Men detta gäller bara om man anger läget
med fyra koordinater. Det visste redan neandertalaren som kastade sten mot ett byte. Men vi
använder också tid som en förändringsparameter. Som jag ser det är det uppenbart att detta är två
olika sätt att använda tidsbegreppet. För mig är detta så självklart att jag har svårt att uttrycka det
tydligare.
Jag färdas med hastigheten c i min koordinattidsriktning. Jag kan varken röra mig fortare eller
långsammare. Men det intressanta är att Pelle kan färdas i en annan riktning. Och under vissa
förutsättningar kan han tala om vad han ser.
__________________
2013-20-02
Om världen är fyrdimensionell kan den avbildas bijektivt på en fyrdimensionell bild. Det betyder att
man till varje bildpunkt knyter en och endast en verklighetspunkt.
Både R^4 och R^(1,3) är fyrdimensionella och det går alltså att lägga en bijektiv bild på dem.
I stället för att lägga bijektiva bilder kan jag lägga en euklidisk bild på R^4 och en minkowskibild på
R^(1,3). Med euklidisk bild menar jag en bild där jag på varje bildpunkt lägger alla
verklighetspunkter med det euklidiska avståndet noll mellan sig. Och med minkowskibild menar jag
en bild där jag lägger alla verklighetspunkter med minkowskiavståndet noll mellan sig på samma
bildpunkt.
Om jag tar en verklighetspunkt så finns det inga andra verklighetspunkter på det euklidiska
avståndet noll. Den euklidiska bilden blir alltså bijektiv. Däremot finns det en grupp
verklighetspunkter som har minkowskiavståndet noll mellan sig. Minkowskibilden blir alltså inte
bijektiv. Jag kan inte återskapa verkligheten från minkowskibilden.
En regel som i den euklidiska bilden pekar ut en bildpunkt pekar entydigt ut en verklighetspunkt. En
regel som i minkowskibilden pekar ut en bildpunkt pekar ut en grupp verklighetspunkter. Detta är en
fundamental skillnad mellan regler i den euklidiska bilden och regler i minkowskibilden. Man kan
med matematiska metoder visa att bildernas regler är fundamentalt olika men det viktiga är att man
vet vari olikheten består.
När man i praktiken försöker använda minkowskibilden upptäcker man snart att den inte räcker. Man
behöver bara försöka följa fasläget i ett växelströmsnät eller räkna på fading mellan signaler med
olika gångväg eller bestämma position med hjälp av satelitklockor för att upptäcka att man måste
komplettera minkowskiavståndet med det euklidiska avståndet.
Jag kan naturligtvis komplettera minkowskibilden med den euklidiska bilden så att jag får en bijektiv
bild men då använder jag ju den euklidiska bilden.
Effekter på ljusstrålar och effekter av en påstådd eter är väl helt enkelt samma sak. Och jag ser
inget konstigt i att ett medium påverkas av acceleration.
Kausalitet är en stor fråga. Det behövs mer än några rader om det.
__________________
2013-02-03
Om jag gör en bijektiv avbildning (A) av verkligheten använder jag en regel som knyter varje
verklighetspunkt till en och endast en bildpunkt. Omvändningen av denna regel lägger tillbaka
bildpunkten på verklighetspunkten och återskapar alltså förlagan från bilden. Om jag så gör en
annan bijektiv bild (B) med en annan regel får jag två olika bilder. Om jag då tillämpar B:s regel på
omvändningen av A:s regel får jag en regel som avbildar A på B. Om två bilder är bijektiva
avbildningar av samma förlaga finns det alltså en regel som avbildar den ena på den andra.
Om världen är symmetrisk kan man dela in den i undergrupper där varje undergrupp har någon
gemensam egenskap. Om man inte är intresserad av förhållandena inom varje undergrupp kan man
använda en icke-bijektiv avbildning där varje bildpunkt inte svarar mot en verklighetspunkt utan mot
en sådan undergrupp.
Om världen har andra icke-materiella egenskaper kommer de inte med i någon form av avbildning.
De ligger alltså helt utanför den här diskussionen.
Jag färdas mot min framtid. Om jag inte gör något är min framtid Vendelsös framtid. Men om jag
tar bilen och kör mot Karlstad där min far bodde ändras min färdriktning så att min framtid blir
Karlstads framtid. Min färdriktning bildar alltså en vinkel med markens färdriktning. När jag ser på
min hastighetsmätare visar den sinus för denna vinkel. Jag brukar se det som att hastighetsmätaren
visar nanosinus som ju är ungefär samma som km/h. När hastighetsmätaren visar 90 färdas jag
alltså med 90 nanosinus mot Karlstads framtid. När jag kommer fram till Karlstads börjar jag lägga
Karlstads dåtid till min dåtid.
När min far levde ringde han ibland och berättade vad som hänt i Karlstad. Utan att min
koordinattidsaxel gått genom Karlstad kunde jag då lägga in en del av Karlstads dåtid i min dåtid.
Jag tror att de flesta människor ser detta som så självklart att det inte behöver formuleras. Men jag
tror att det är viktigt att göra det så att jag kan se mer i detalj på vad det innebär.
__________________
2013-02-03
Ja. Det är ju som du säger inledningsvis så att man kan se världen på olika sätt (olika metriker). En
fördel med att vrida koordinatsystemet med arcsin(v/c) är att när du kommer till 90 grader byter
tidsaxeln plats med en rumsaxel och om du fortsätter vridningen kommer tiden att gå bakåt sett från
en utomstående betraktare. För den som faller in i hålet blir däremot allt oförändrat. Frågan om hur
man beskriver ett fall in i ett svart hål var en anledning till att jag tyckte den beskrivningen var
intressant.
__________________
2013-02-04
PuffTheDragon har på https://www.flashback.org/sp37376762 en beskrivning av situationen vid ett
svart hål.
Om vi hittar ett svart hål inom räckhåll kommer vi att kunna skicka ett rymdskepp genom det. Vad
händer när skeppet passerar genom hålet?
Antag att det finns två instrument på skeppets instrumentbräda. Det ena är en radiostyrd klocka som
visar tid enligt ett atomur på Jorden och det andra är en avståndsmätare som visar avståndet från
Jorden. Före start är det lätt att se vilket som är avståndsmätare och vilket som är klocka. Klockan
går och avståndsmätaren står stilla. När skeppet tar fart börjar avståndsmätaren att gå och klockan
saktar in.
Skeppet får falla i fritt fall mot hålet. När det når händelsehorisonten har det kommit upp i
ljushastighet. Klockan har stannat men avståndsmätaren går på samma sätt som klockan gjorde
före start. Klocka och avståndsmätare ser alltså ut att ha bytt plats. En av mina rumsaxlar har blivit
skeppets koordinattidsaxel och min koordinattidsaxel har blivit en av skeppets rumsaxlar. Men
frånsett att instrumenten bytt plats märker besättningen ingenting av händelsehorisontpassagen.
Ombord på skeppet fungerar alla naturlagar som vanligt. Skeppets koordinatsystem har vridits i
förhållande till mitt koordinatsystem men det har inte genomgått några inre förändringar. En vanlig
klocka ombord på skeppet går som avståndsmätaren.
När skeppet kommit innanför händelsehorisonten börjar klockan på instrumentbrädan att gå
baklänges och avståndsmätaren saktar in. Skeppet kan nu inte längre kommunicera med Jorden
men för besättningen är allt annat som vanligt. Man fortsätter att skriva i loggboken. Man daterar
loggboken både efter instrumentbrädesklockan, avståndsmätaren och den vanliga klockan.
När skeppet passerat hålets centrum har det rörelseenergi nog att fortsätta ut ur hålet. När det på
nytt passerar händelsehorisonten kan det åter börja rapportera till Jorden. Vi kan då få veta något
om hur det ser ut inne i hålet.
__________________
2013-02-04
Världen i sig har inga koordinater. För att få koordinater som jag kan använda måste jag avbilda
världen på ett koordinatsystem. Vilken typ av koordinater jag då får beror på vilken typ av
koordinatsystem jag valt och vilken typ av avbildning jag använt.
Som jag ser det har jag fyra koordinataxlar varav en pekar mot min framtid. Om vi har en väg som
går mellan gården och handelsboden kan jag och min kompis gå mot handelsboden medan du går
mot gården. Min koordinattidsaxel pekar då mot handelsbodens framtid och din pekar mot gårdens
framtid. Mitt på vägen möts vi och konstaterar att våra framtider ligger mycket nära varandra men
att det finns en liten skillnad som gör att vi kommer att ha ett rumsavstånd när vi kommer fram.
Jag och allt i min närmaste omgivning färdas mot nästan samma framtid. Det innebär att det
vanligtvis är självklart vad som skall vara koordinattidsriktning. Men vad som är koordinattidsriktning
är inte en egenskap hos världen. För ett rymdskepp som passerar mig med en hastighet som ligger
nära ljushastighet kan det som för mig är rum vara koordinattid.
__________________
2013-02-06
Du har helt rätt i att R^4 , R^(3,1) och R^(2,2) alla är fyrdimensionella och alltså kan ta emot en
bijektiv bild av verkligheten. Om information kunde överföras med oändlig hastighet skulle det inte
spela någon roll om man separerade axlarna eller inte. Då kunde man hantera varje koordinat som
oberoende av de övriga. Men om det finns en maximal hastighet blir inte tid och rum alltid
oberoende av varandra. Om jag sänder en signal för att påverka en stjärna som ligger på
rumsavståndet en miljon ljusår tar det två miljoner år innan jag får veta resultatet. Stjärnan är
alltså avlägsen både i tid och rum. Och när man transformerar mellan system som rör sig i
förhållande till varandra får rumskoordinater tidsprojektioner och tvärtom. Frågan är då hur man
hanterar detta.
Om man har separerat en axel som tidsaxel kan man inte direkt vrida in den i rummet för att kunna
projicera rums- och tidskoordinater på varandra. Man behöver använda en icke-ortogonal transform
för att projicera rum och tid på varandra. Den fråga jag en gång i tiden ställde mig var: "Kan jag
inte i stället vrida det ortogonala systemet i R^4?" Det kan jag naturligtvis göra. Världen bryr sig inte
om hur jag avbildar den eller hur jag hanterar dess bild. Frågan är om jag kan tolka en sådan bild
på ett vettigt sätt. Jag har nu använt det här synsättet i några årtionden och inte funnit något som
talar mot det. Men det betyder naturligtvis inte att det är det enda rätta, bara att det ibland är
användbart.
När det gäller kausaliteten så menar jag att vi ibland använder tid som en förändringsparameter
alltså som ett sätt att ordna händelser i löpande följd. Som jag ser det har detta inte direkt med
läge att göra. Det är därför jag ser parametertiden som något annat än koordinattiden. Kausalitet
avgörs alltså av parametertid. Om det finns ett orsaksamband mellan två händelser är den med
lägst parametertid orsak.
När parametertiden går färdas jag längs min koordinattidsaxel. De punkter jag lämnar kallar jag
dåtid, den punkt där jag befinner mig kallar jag nu och de punkter som ligger framför mig kallar jag
framtid. Pelle som far förbi i ett rymdskepp gör likadant med sin koordinattidsaxel. Att det råkar vara
en av mina rumsaxlar är inget som han märker något av.
Om jag vill påverka en händelse på rumsavstånd måste jag skicka en påverkanssignal. Den punkt på
min koordinattidsaxel där jag gör det kallar jag händelsens påverkansnu. Den punkt på min
koordinattidsaxel där jag befinner mig vid den parametertid som händelsen inträffar vid kallar jag
händelsens samtidsnu. Den punkt på min koordinattidsaxel där jag befinner mig där
bekräftelsebilden av händelsen når mig kallar jag händelsens observationsnu. Vid händelsens
påverkansnu och observationsnu är minkowskiavståndet till händelsen noll.
Jag sätter v/c = sin(a) där (a) är min vridningsvinkel. Eftersom sin inte kan bli större än ett behöver
jag då ingen begränsning av vridningsvinkeln. Även vridning mer än 90 grader kan ges en tolkning
vilket kommer att bli aktuellt när vi någon gång i framtiden börjar färdas genom svarta hål.
Lika lite som koordinatsystemet finns i verkligheten finns vridningsvinkeln i verkligheten. Den är en
egenskap hos det koordinatsystem jag valt. Men skall man leta efter en känguru är det kanske där
man skall leta. Men det är inte lätt att hitta genomförbara experiment som kan visa vad som gäller.
För de hastigheter vi normalt hanterar är skillnaden mellan sin och tan inte mätbara.
__________________
2013-02-07
Jag vet inte hur man hanterar bilder men vi kanske återigen kan använda dbshw:s bild
Vi försöker igen.
Jag använder din figur. Som jag ser det är den blå linjen Pelles t-axel. Längden i den blå riktningen
är alltså vad Pelles stoppur visar för Pelle. Han springer nu så att den blå sträckan som du angett
som "längre än 50 m/0,99c" blir 50/0,99c. Den röda sträckan som du angett som "50 m/0,99c" är
min tolkning av Kalles signal vilken alltså är mindre än 50/0,99c. Genom att Pelle delvis springer i
mitt rum rör han sig långsammare i min koordinattidsriktning (t-riktning).
Minkowskimetriken bygger på tanken att det finns ett tidsavstånd som kan uppväga ett rumsavstånd
så att resultatet blir noll. Om tidsavståndet är lika med rumsavståndet blir Minkowskiavståndet noll.
Detta fungerar i många fall eftersom vi upplever bilden av en händelse som om den var händelsen.
Vi är tydligen överens om att två punkter med Minkowskiavståndet noll kan ha ett reellt avstånd.
Som jag ser det betyder det att man även måste hålla reda på det reella avståndet vilket
Minkowskimetriken inte gör. Som jag ser det kan Minkowskimetriken komplettera den reella
metriken men inte ersätta den.
__________________
2013-01-14
Om jag ser en stjärna explodera säger jag: "Nu exploderade stjärnan."
Så tänker jag efter och ändrar det till: "Nu blev minkowskiavståndet till stjärnexplosionen noll. Hur
skall jag lägga in det i mitt koordinatsystem?"
Om stjärnan ligger en miljon ljusår bort och om det hade funnits en enorm klocka på stjärnan som
jag kunde se skulle jag se att klockan visade en tidpunkt för en miljon år sedan. Jag ritar då ett
koordinatsystem med en t-axel och en x-axel och med mig i origo. Så lägger jag in
stjärnexplosionen vid t lika med minus en miljon år och x lika med en miljon ljusår.
Stjärnexplosionens koordinattid i mitt system blir alltså minus en miljon år. Sedan dess har
parametertiden gått och jag ha färdats längs min t-axel så att jag nu kommit till origo. Och bilden av
stjärnexplosionen har färdats längs min x-axel så att den nu nått origo där jag kan se den. Från
origo är avståndet i t-riktningen lika stort som avståndet i x-riktningen vilket innebär att
minkowskiavståndet är noll.
Jag tror att detta är ett mycket vanligt sätt att se situationen.
__________________
2013-01-15
Det är mycket möjligt att man inte behöver något annat avståndsbegrepp i relativitetsteori. Men
relativitetsteori är inte hela världen. Den har funnits i cirka hundra år men den reella metriken har vi
använt i många tusen år. Jag tar inte ett steg utan en mängd avståndsbedömningar till väggar. golv.
möbler med mera.
Du har sagt någon gång att man kan bortse från relativitetsteori i vardagen. Att man alltså kan se
relativitetsteori som en spekulation fristående från vardagens verklighet. Så var det kanske för
hundra år sedan men det har hänt en del sedan dess. Vi möter idag en hel del fenomen där
ljushastigheten spelar en viktig roll.
Hela radartekniken bygger på att rumsavståndet är lika med tidsavståndet när minkowskiavståndet
är noll. I GPS använder vi skillnader i koordinattid mellan reellt synkrona klockor placerade i sateliter
med kända lägen. Vi bygger allt större växelströmsnät med mimkowskisynkronism. När jag bygger
ett kretskort för att hantera datorpulser måste jag tänka på att en nanosekundpuls inte är längre än
en fot. När jag ringer till Australien får jag ibland en fördröjning som kräver en viss samtalsdisiplin.
Vi är på väg mot rymdfärder över avstånd där skillnaden mellan parametertid och koordinattid
spelar stor roll.
Allt oftare dyker de samband som ursprungligen härleddes via relativitetsteori upp i andra
sammanhang och med annan härledning. Som jag ser det är det viktigt att ha någon uppfattning om
hur olika synsätt hänger samman.
Minkowskimetriken är inte en egenskap hos verkligheten. Den är en transform som skapats via en
transformationsregel. När jag fotograferade med negativ färgfilm fick jag en en bild där färgerna
transformerats via en transformationsregel. Men eftersom denna regel var bijektiv kunde man vända
på regeln och kopiera bilderna tillbaka till förlagans färger. På samma sätt transformerar man till
minkowskimetriken via en transformationsregel. Men genom att man låser ett samband mellan
tidsavstånd och rumsavstånd blir denna transform inte bijektiv. Det går alltså inte att från
minkowskimetrikens bild bestämma reella avstånd. Minkowskimetriken kan därför bara komplettera
den reella metriken, inte ersätta den.
Det är inte något fel i att använda transformer. Laplace-transformer är mycket användbara inom
reglerteknik, Fourier-transformer är utmärkta när man bygger förstärkare och minkowskimetriken
har ett klart tillämpningsområde. Men en transform är aldrig det enda möjliga synsättet.
Det finns en egendomlig inställning att alla måste se allt på samma sätt. Så är det inte. Det är
genom att vi ser saker på olika sätt som vi kan hitta nya möjligheter. Men då behöver vi tala om för
varandra vad vi ser och naturligtvis måste vi vara öppna för att anpassa vårt synsätt så att det
stämmer med de fenomen som vi observerar.
__________________
2013-01-17
Det reella avståndet till en händelse är roten ur (x^2+y^2+z^2+tc^2).
En händelse kan orsaka en bild som med hastigheten c utbreder sig i alla riktningar. Avståndet till
händelsens bild ärroten ur ( x^2+y^2+z^2-tc^2). Minkowskiavståndet till en händelse är alltså
avståndet till händelsens bild. Eftersom mottagandet av händelsens bild är mitt enda sätt att få veta
något om händelsen kan jag i många fall ersätta händelsen med händelsens bild.
Världen påverkas inte av mitt sätt att avbilda den. Jag kan välja om jag vill avbilda på ett
koordinatsystem med raka eller krokiga, reella eller imaginära axlar. En bild av världen avbildar även
alla fenomen som vi observerat. Det kan vara lämpligt att välja en avbildning som ger en lättanvänd
beskrivning av världen inklusive dess fenomen. Även om jag inte lyckats beskriva det tillräckligt
tydligt har jag försökt tala om att jag använder ett fyrdimensionellt koordinatsystem med raka
ortogonala reella axlar. Om jag i detta beskriver rumshastighet som en vridning av
koordinattidsaxeln så att rumshastigheten blir lika med c gånger sinus för vridningsvinkeln får jag
enkla uttryck för längdkontraktionen och tidsdilationen.
Varje gång en detekterbar händelse inträffar någon stans i universum förändras det och
parametertiden inkrementeras. Parametertid är alltså antalet minsta detekterbara händelser i
universum. Ett antal är en skalär storhet. Varje förändring av universum innebär att mitt läge i
förhållande till mitt omgivande universum förändras. Det lägger jag in i mitt koordinatsystem som att
jag flyttar mig en tidsenhet lika med c längdenheter längs min koordinattidsaxel när parametertiden
ökar med en tidsenhet.
En klocka räknar antalet händelser i ett tidsgivande element. Eftersom det tidsgivande elementet är
en viss andel av hela universum blir detta ett mått på antalet händelser i hela universum. En klocka
mäter alltså parametertid.
Om det vid en händelse finns en klocka kommer bilden av klockan att följa med händelsens bild.
Denna bild av klockan visar då händelsens koordinattid i mitt koordinatsystem.
__________________
2013-01-21
Som jag ser det visar MM:s försök ingenting annat än att Jorden (och mätanordningen) ligger stilla i
förhållande till den eter som den svävar i. Av detta kan man varken dra slutsatsen att
ljushastigheten alltid är konstant eller att ljusstrålar alltid är raka. Det finns mycket att säga om
detta och jag funderar på om jag kan åstadkomma en begriplig sammanfattning.
När jag läste om relativitetsteori gjorde man ett stort nummer av att man kan inte veta något om en
händelse förrän man nås av händelsens bild. Man hävdade att det innebär att man kan ersätta
händelsen med händelsens bild. Avståndet till händelsens bild kan man skriva som roten ur (x^2+y^
2+z^2-tc^2). Men argumentet håller inte. Bilden av en händelse är något annat än händelsen.
Om jag kör in i en blockerad vägkorsning växelverkar jag med händelsen "blockerad korsning".
Resultatet blir en händelse som kallas "krock". Om jag bromsar in när jag nås av bilden av
"blockerad korsning" växelverkar jag med bilden av "blockerad korsning". När korsningen blir fri kan
jag köra igenom rumskoordinaterna för "blockerad korsning" men eftersom tidskoordinaten då blir
en annan får jag ingen växelverkan med "blockerad korsning".
Som jag ser det kan man använda Minkowskimetrik för händelsers bilder. Det är inget fel i det. Det
kan i många fall vara ett användbart sätt att hantera problem. Men det ersätter inte behovet av att
hantera händelser.
__________________
2013-01-22
Som ett plankton svävar i en havsström svävar jag i en eter som blåser med ljushatighet i en
riktning som jag kallar koordinattidsriktningen. Föremål i min omgivning svävar i samma eter och ser
ut att stå stilla. Men etervindens riktning är inte alltid exakt densamma. Om den avviker vid ett
föremål ser jag det som att föremålet rör sig i förhållande till mig.
När jag kör med min bil vrider jag min koordinattidsaxel så att den bildar en vinkel med markens
koordinattidsruktning. Jag ändrar alltså etervindens riktning kring bilen. På samma sätt som luften i
kupen följer med bilen följer etern kring bilen med bilen. En MM-mätare i bilen kommer alltså att
visa att bilen ligger stilla i förhållande till etern i bilen liksom en MM-mätare på marken visar att
marken ligger stilla i förhållande till etern vid marken.
Jag kan inte komma från marken till bilen utan att accelerera. Mellan bilen och marken finns alltså
ett accelerationsskikt det vill säga ett gravitationsfält. Ljusstrålar kröks i ett gravitationsfält. När jag
tittar ut genom vindrutan på bilen ser jag alltså ljusstrålar som krökts i ett gravitationsfält.
När jag tittar ner i vattnet händer det att jag ser en fisk. Om jag med ett spjut hugger mot bilden av
fisken bommar jag. Ljusstrålarna kröks vid vattenytan så att bilden av fisken inte sammanfaller med
fisken. SR är ett sätt att hantera detta genom att flytta fisken till bilden så att man kan använda raka
ljusstrålar. En annan möjlighet är att räkna med krökta ljusstrålar som flyttar bilden till fisken.
När jag tittar ut genom vindrutan blir ljuskrökningen så liten att den inte spelar någon roll. Och för
hundra år sedan var det knappast något annat än en vetenskaplig spekulation. Men om jag till
exempel jobbar med tröghetsnavigering använder jag gravitationsfältspassagerna för att bestämma
hastighet så att jag med hjälp av hastighet och en klocka kan bestämma läge. Här spelar även
obetydliga gravitationsfält vid färdens början en stor roll.
Jag har aldrig funderat på om begreppet "händelsens bild" är vanligt. Bara på om det är begripligt
och det tror jag att det är.
__________________
2013-01-26
För att hantera min värld behöver jag en bild där jag kan lägga in ett koordinatsystem så att jag får
koordinater som jag kan räkna med. Om jag gör en bijektiv avbildning innehåller bilden all
information om världen. Det går då att från bilden återskapa världen och alla bildens egenskaper
kommer från världen. Om jag förenklar bilden genom att avbilda flera punkter på samma bildpunkt
blir min avbildning inte bijektiv. Min bild kommer då att innehålla dels egenskaper som kommer från
världen, dels egenskaper som kommer från avbildningsfel.
1872 lade Felix Klein fram det så kallade Erlangenprogrammet där avbildningar indelas i klasser
efter vad som är invariant vid transformationer. Minkowskiavbildning och reell avblidning har olika
invarianter och tillhör alltså olika klasser. Men om avbildningen är bijektiv ger den, oberoende av
klass, en fullständig bild som enbart innehåller verklighetens egenskaper. En beskrivning av ett
fenomen i den ena avbildningen har då sin motsvarighet i en beskrivning i den andra avbildningen.
Vår reella avbildning är ett självklart inslag i vårt medfödda och vårt inlärda beteende.
Relativitetsteorin medförde att man såg en del samband som man inte tidigare hade sett. Men det
innebär naturligtvis inte att man bara kan avbilda världen på ett enda sätt. En bijektiv avbildning
enligt Minkowski och en bijektiv reell avbildning måste beskriva fenomen på sätt som ger samma
försöksresultat. Världen bryr sig naturligtvis inte om vilken avbildningsklass jag valt att använda.
En tredimensionell reell avbildning är inte bijektiv. När jag projicerar en fyrdimensionell värld på en
tredimensionell bild får jag samma typ av projektionsfel som när jag projicerar en klotyta på ett plan
(jag tycker trots allt att liknelsen ger en uppfattning av problemet). Minkowskiavbildningen är
fyrdimensionell och om den är bijektiv måste det gå att göra en bijektiv reell avbildning. Allt som kan
beskrivas i den ena avbildningen har då sin motsvarighet i den andra.
Som jag ser det blir det då intressant att ställa frågan: "Hur gör jag en reell avbildning som visar
motsvarigheten till de samband som relativitetsteorin påvisade?".
Man kan naturligtvis invända att de samband som man påvisade inom relativitetsteorin nu är
välkända och inte behöver någon annan beskrivning men jag tror att en bra reell beskrivning kan
visa oss nya oväntade samband. Och det skulle ha fördelen att vi kan betrakta världen utan att
behöva fundera på vilken avbildningsklass vi skall välja. Och jag tror att det är intressant oberoende
av om man kallar det fysik eller vardagshantering eller något annat.
__________________
2013-01-27
Visst ger olika avbildningar olika bilder där samband ser olika ut. Det är ju det som är poängen med
att använda olika avbildningar. Och du har rätt i att det kan hända att några samband som blir enkla
i Minkowskis avbildning bli svårhanterliga i andra avbildningar. Har du något bra exempel på de
symmetrier du pratar om? Något som är baserat på odiskutabla mätningar.
I många tusen år har vi använt reell avbildning. Vi har sett samband som vi betraktar som så
självklara att vi inte längre ser dem. Det är inte så att vi bara projicerar på ett tredimensionellt rum
genom att sätta dt=0. Vi är mycket medvetna om tidskoordinaten även om vi inte alltid formulerar
detta. Vi stoppar mat i munnen utan att med formler beskriva hur det går till.
För drygt hundra år sedan provade vi att använda Minkowskis avbildning och upptäckte att den
visade några samband som vi inte sett tidigare. Det var ju intressant men det betydde naturligtvis
inte att vi funnit den enda rätta avbildningen. Fortfarande lever många människor hela sitt liv med
daglig användning av reell avbildning men utan att ägna en tanke åt Minkowskis avbildning.
Jag vet inte varför du återkommer till att ljushastigheten skall vara konstant. I den värld jag ser är
den inte det. Jag ser c som min hastighet i koordinattidsriktningen, alltså som omräkningsfaktor
mellan längdenheter och tidsenheter.
Och en liten detalj. Om jag projicerar ett klot på ett plan blir väl projektionen RÄTT i en punkt. Och
om jag avbildar ett tredimensionellt klot på ett tvådimensionell plan tar jag väl bort en dimension.
Det spelar ingen roll eftersom det bara handlar om en liknelse men jag undrade vad du menar.
__________________
2013-01-28
Längdkontraktionen och tidsdilationen är ju väldokumenterade fenomen så låt oss börja med det.
Då är vi tillbaka i Pelles lada. Förra gången tyckte du att jag uttryckte mig otydligt så jag tänker ta
det bitvis så får vi se om det blir begripligt.
Först en viktig skillnad mellan SO(3,1) och SO(4).
I SO(3,1) är en koordinataxel speciell. Tid är något annat än längd och man kan direkt på
koordinatsystemet se vilken axel som är tidsaxel. Men om det finns en ändlig hastighet för
informationsöverföring blir längd och tid beroende av varandra. Detta beroende lägger du i
invarianten. Genom att använda en icke-ortogonal transform får du en koppling mellan
tidskoordinater och längdkoordinater. Det är ju det som är tricket med lorentztransformen.
I SO(4) är alla koordinater av samma typ. Jag kan inte, bara genom att se på koordinatsystemet,
avgöra vilken axel som är tidsaxel. Jag måste skilja mellan rum och tid på något annat sätt. När jag
ser på en klocka ser jag att den visar allt högre värden. Om jag avsätter klockslag och årtal på en
koordinataxel får jag alltså värden som ständigt ökar. Jag färdas alltså längs denna koordinataxel. I
SO(4) kan jag vrida mitt koordinatsystem så att bara en av mina fyra koordinater ökar. Jag kan
alltså lägga en koordinataxel i min färdriktning. Jag kallar den koordinataxeln för koordinattidsaxel.
Pelle gör likadant men det är inte säkert att han färdas i samma riktning som jag och det är alltså
inte säkert att hans koordinattidsaxel blir parallell med min. Det som för mig är rum kan vara tid för
Pelle och tvärtom. Den koppling mellan tid och rum som du i SO(3,1) beskriver med hjälp av en icke-
ortogonal transform beskriver jag i SO(4) som en vridning av koordinattiden.
Under min livstid kommer jag bara att passera de punkter som ligger på min koordinattidsaxel. Om
jag inte går in i ladan ligger den i mitt rum och sträcker sig i koordinattid utefter min
koordinattidsaxel utan att min koordinattidsaxel går in i ladan. Jag kommer alltså inte att passera
genom ladan. För att Pelle skall kunna ta sig igenom ladan måste han vrida sin koordinattidsaxel så
att den går genom ladan. Pelle och jag får alltså icke-parallella tidsaxlar.
Är vi överens om att man kan göra så? Om att detta sätt att se på världen inte strider mot några
kända regler?
_________________
2013-01-29
Om det finns en högsta möjliga hastighet c kan jag använda denna för att omvandla mellan
tidsenheter och längdenheter. c har egentligen inte med ljushastighet att göra annat än att
ljushastigheten i en viss situation är den högsta hastighet vi funnit. Jag jobbade en gång i tiden med
hjälpmedel för blinda bland annat frågan om hur man skapar en avståndsuppfattning utan hjälp av
synen. Här kan man använda ljudhastigheten som c. Men det viktiga är att c är en ändlig konstant.
När jag graderar min koordinattidsaxel tar jag en klocka. När klockan (parametertiden) går en
tidsenhet avsätter jag en tidsenhet, det vill säga c längdenheter, på min koordinattidsaxel
(koordinattid). Jag färdas alltså en tidsenhet, det vill säga c längdenheter, i koordinattidsriktningen
när paramertiden går en tidsenhet.
Jag kan dividera rumshastigheten v med c. Eftersom c är största möjliga hastighet kommer v/c att
ligga mellan -1 och 1. En storhet som ligger mellan -1 och 1 kan jag skriva som sin(a). Detta är ett
ganska vanligt sätt att hantera sådana storheter. Om jag sätter v/c = sin(a) blir lorentzkontraktionen
cos(a).
Jag återkommer till användningen av (a) men först är frågan: "Kan jag göra så här?" Har jag gjort
något som strider mot kända regler?
__________________
2013-01-30
Om jag anger en punkts läge med fyra av varandra oberoende (ortogonala) koordinater blir
lägesangivelsen fullständig. Om jag kastar en sten mot ett byte och alla stenens fyra koordinater
överensstämmer med bytets motsvarande koordinater träffar jag alltid. Så länge någon av stenens
koordinater avviker från bytets motsvarande koordinat träffar jag aldrig. En avbildning på ett
fyrdimensionellt ortogonalt koordinatsystem är alltså bijektiv.
Såväl en avbildning på SO(3,1) som en avbildning på SO(4) är bijektiv. Båda ger alltså en fullständig
beskrivning av verkligheten som innebär att verkligheten kan återskapas från beskrivningen. Världen
bryr sig inte om om jag använder ett koordinatsystem med fyra likadana axlar eller ett
koordinatsystem där jag särbehandlar en axel. Men avbildningarna blir olika och jag kan inte
använda samband från SO(3,1) i SO(4). Däremot måste naturligtvis utfallet av försök bli samma
oavsett om jag använt en beskrivning i SO(3,1) eller SO(4).
Om ljushastigheten är densamma i alla riktningar blir ljusstrålar raka. För att en ljusstråle skall
krökas måste ljushastigheten vara lägre längs innerkurvan än längs ytterkurvan. MM:s försök visade
att ljushastigheten INOM ett referenssystem är lika i alla riktningar. Av det kan man inte dra några
slutsatser som handlar om övergångar mellan referenssystem.
Jag kan inte komma från ett referenssystem till ett annat utan acceleration. Mellan två
referenssystem finns alltså ett accelerationsfält alltså ett gravitationsfält. Stjärnan vid
solförmörkelsen visar att ljuset böjs i solens gravitationsfält. Eftersom den enda kunskap vi har om
vad som finns på avstånd kommer från ljus och liknande fenomen som når oss ser vi inte om
ljusstrålar är raka eller krokiga. I en prismakikare är en ljusstråle långt ifrån rak men när vi tittar i
kikaren märker vi ingenting av dessa krokar.
Med raka ljusstrålar kan man bara se rakt. En ljusstråle längs x-axeln visar enbart vad som händer
på x-axeln. Man kan inte set runt ett hörn. Men en krokig ljusstråle kan ha varit inne i en annan
dimension. Om ljusstrålar kan vara krokiga kan det längs x-axeln komma en stråle som visar vad
som hänt på t-axeln. x-koordinaterna blir då inte helt oberoende av t-koordinaterna.
Hur skall man hantera att ljusstrålar böjs vid övergången mellan två referenssystem?
En möjlighet är att med en icke-ortogonal transform vrida rummet så att tidsaxeln får en
rumsprojektion. Man kan då använda koordinatsystem som särbehandlar tidskoordinaten SO(3,1).
En annan är att vrida hela koordinatsystemet. Då ändras vad som är tid och vad som är rum vilket
kräver att alla axlar betraktas som likvärda och utbytbara SO(4).
Relativitetsteorin beskriver ett sätt att transformera mellan SO(3,1)-system på sådant sätt att
ljusstrålar beskrivs som raka. Det betyder naturligtvis inte att de ÄR raka. Begreppen rak och krokig
hör till vår beskrivning av världen. Det är först när vi beskriver en ljusstråle som vi kan tala om rak
eller krokig.
Världen kan beskrivas i SO(3,1) eller SO(4) (och på andra sätt). Men beskrivningen blir olika och
man kan inte utan vidare ta samband från en beskrivning i SO(3,1) och använda dem i SO(4). Varje
beskrivning måste bygga på sina egna regler och övergång mellan beskrivningarna måste göras
med hjälp av regelövergångar.
__________________
2013-01-31
Då var det dags för längdkontraktion och tidsdilation i SO(4).
När Pelle springer genom ladan skall han se en kortare lada och jag skall se en Pelle som färdas
långsammare än jag i min koordinattidsriktning. Blir det så?
Sätt v/c till sin(a) och tolka (a) som vinkeln mellan min och Pelles koordinattidsaxlar. Då blir
lorentzkontraktionen cos(a). Och vinkeln mellan min och Pelles x-axel blir också (a). I Pelles system
får ladan en komposant i x-led och en komposant i t-led. x-komposanten blir ladans längd gånger
cos(a) (längdkontraktion) och t-komposanten blir ladans längd gånger sin(a).
När jag färdas T enheter längs min koordinattidsaxel färdas Pelle T enheter längs sin
koordinattidsaxel. Men eftersom Pelle delvis färdas i mitt rum, alltså i min x-riktning, kommer han att
färdas långsammare i min koordinattidsriktning. Han färdas bara Tcos(a) i min koordinattidsriktning
(tidsdilation) och i min x-riktning färdas han Tsin(a).
__________________
2013-02-01
Jag är naturligtvis medveten om att du kan ha rätt. Men om jag skall felförklara den avbildning som
människor använt i tusentals år och funnit användbar och pålitlig vill jag ha mycket påtagliga bevis.
Att man kan använda en annan avbildning är inte något bevis på att den gamla är fel Men - visst.
Jag tänker ibland på vilka konsekvenser det skulle ha men först vill jag veta hur jag kan använda den
gamla vanliga avbildningen.
Det är uppenbart att vi använder begreppet tid på sätt som vi inte kan använda rumskoordinater.
Som jag ser det beror det på att vi använder tid som ett sammanfattningsbegrepp för två olika
begrepp, parametertid och koordinattid. Parametertid är en skalär förändringsparameter,
koordinattiden är en koordinat av samma typ som rumskoordinaterna.
Om c är högsta möjliga hatighet och jag färdas med hastigheten c i koordinattidsled kan jag ju inte
röra mig fritt i koordinattidsled. Men det finns mycket att säga om detta. Jag skall försöka
återkomma.
Så vitt jag kunnat finna handlar alla MM-mätningar om mätningar inom ett referenssystem. Inga
delar av mätanordningarna rör sig i förhållande till varandra med hastigheter som närmar sig
ljushastighet. Då säger inte mätningarna något om övergångar mellan referenssystem.
Maxwells ekvationer säger inte alls att ljushastigheten är densamma i alla referenssystem. De säger
att ljushastigheten är ett genom roten ur produkten av det ljusbärande mediets
dielektricitetskonstant och magnetiska permeabilitet. Det är till exempel väl känt att ljushastigheten i
glas är lägre än i luft. Det är grunden för hela optiken. Och det handlar inte om att ljuset "studsar"
sig genom glaset. Vi kan mäta dielektricitetskonstant och magnetisk permeabilitet med metoder som
inte använder ljus och se att resultatet stämmer.
__________________
2013-02-01
Om avståndet mellan två punkter i euklidisk metrik är noll sammanfaller punkterna. Det är i så fall
en dubbelräkning av samma punkt. Det är ju detta som är innebörden i att avbildningen är bijektiv.
Man lägger aldrig två olika punkter med avståndet noll. Men detta gäller bara om man anger läget
med fyra koordinater. Det visste redan neandertalaren som kastade sten mot ett byte. Men vi
använder också tid som en förändringsparameter. Som jag ser det är det uppenbart att detta är två
olika sätt att använda tidsbegreppet. För mig är detta så självklart att jag har svårt att uttrycka det
tydligare.
Jag färdas med hastigheten c i min koordinattidsriktning. Jag kan varken röra mig fortare eller
långsammare. Men det intressanta är att Pelle kan färdas i en annan riktning. Och under vissa
förutsättningar kan han tala om vad han ser.
__________________
2013-20-02
Om världen är fyrdimensionell kan den avbildas bijektivt på en fyrdimensionell bild. Det betyder att
man till varje bildpunkt knyter en och endast en verklighetspunkt.
Både R^4 och R^(1,3) är fyrdimensionella och det går alltså att lägga en bijektiv bild på dem.
I stället för att lägga bijektiva bilder kan jag lägga en euklidisk bild på R^4 och en minkowskibild på
R^(1,3). Med euklidisk bild menar jag en bild där jag på varje bildpunkt lägger alla
verklighetspunkter med det euklidiska avståndet noll mellan sig. Och med minkowskibild menar jag
en bild där jag lägger alla verklighetspunkter med minkowskiavståndet noll mellan sig på samma
bildpunkt.
Om jag tar en verklighetspunkt så finns det inga andra verklighetspunkter på det euklidiska
avståndet noll. Den euklidiska bilden blir alltså bijektiv. Däremot finns det en grupp
verklighetspunkter som har minkowskiavståndet noll mellan sig. Minkowskibilden blir alltså inte
bijektiv. Jag kan inte återskapa verkligheten från minkowskibilden.
En regel som i den euklidiska bilden pekar ut en bildpunkt pekar entydigt ut en verklighetspunkt. En
regel som i minkowskibilden pekar ut en bildpunkt pekar ut en grupp verklighetspunkter. Detta är en
fundamental skillnad mellan regler i den euklidiska bilden och regler i minkowskibilden. Man kan
med matematiska metoder visa att bildernas regler är fundamentalt olika men det viktiga är att man
vet vari olikheten består.
När man i praktiken försöker använda minkowskibilden upptäcker man snart att den inte räcker. Man
behöver bara försöka följa fasläget i ett växelströmsnät eller räkna på fading mellan signaler med
olika gångväg eller bestämma position med hjälp av satelitklockor för att upptäcka att man måste
komplettera minkowskiavståndet med det euklidiska avståndet.
Jag kan naturligtvis komplettera minkowskibilden med den euklidiska bilden så att jag får en bijektiv
bild men då använder jag ju den euklidiska bilden.
Effekter på ljusstrålar och effekter av en påstådd eter är väl helt enkelt samma sak. Och jag ser
inget konstigt i att ett medium påverkas av acceleration.
Kausalitet är en stor fråga. Det behövs mer än några rader om det.
__________________
2013-02-03
Om jag gör en bijektiv avbildning (A) av verkligheten använder jag en regel som knyter varje
verklighetspunkt till en och endast en bildpunkt. Omvändningen av denna regel lägger tillbaka
bildpunkten på verklighetspunkten och återskapar alltså förlagan från bilden. Om jag så gör en
annan bijektiv bild (B) med en annan regel får jag två olika bilder. Om jag då tillämpar B:s regel på
omvändningen av A:s regel får jag en regel som avbildar A på B. Om två bilder är bijektiva
avbildningar av samma förlaga finns det alltså en regel som avbildar den ena på den andra.
Om världen är symmetrisk kan man dela in den i undergrupper där varje undergrupp har någon
gemensam egenskap. Om man inte är intresserad av förhållandena inom varje undergrupp kan man
använda en icke-bijektiv avbildning där varje bildpunkt inte svarar mot en verklighetspunkt utan mot
en sådan undergrupp.
Om världen har andra icke-materiella egenskaper kommer de inte med i någon form av avbildning.
De ligger alltså helt utanför den här diskussionen.
Jag färdas mot min framtid. Om jag inte gör något är min framtid Vendelsös framtid. Men om jag
tar bilen och kör mot Karlstad där min far bodde ändras min färdriktning så att min framtid blir
Karlstads framtid. Min färdriktning bildar alltså en vinkel med markens färdriktning. När jag ser på
min hastighetsmätare visar den sinus för denna vinkel. Jag brukar se det som att hastighetsmätaren
visar nanosinus som ju är ungefär samma som km/h. När hastighetsmätaren visar 90 färdas jag
alltså med 90 nanosinus mot Karlstads framtid. När jag kommer fram till Karlstads börjar jag lägga
Karlstads dåtid till min dåtid.
När min far levde ringde han ibland och berättade vad som hänt i Karlstad. Utan att min
koordinattidsaxel gått genom Karlstad kunde jag då lägga in en del av Karlstads dåtid i min dåtid.
Jag tror att de flesta människor ser detta som så självklart att det inte behöver formuleras. Men jag
tror att det är viktigt att göra det så att jag kan se mer i detalj på vad det innebär.
__________________
2013-02-03
Ja. Det är ju som du säger inledningsvis så att man kan se världen på olika sätt (olika metriker). En
fördel med att vrida koordinatsystemet med arcsin(v/c) är att när du kommer till 90 grader byter
tidsaxeln plats med en rumsaxel och om du fortsätter vridningen kommer tiden att gå bakåt sett från
en utomstående betraktare. För den som faller in i hålet blir däremot allt oförändrat. Frågan om hur
man beskriver ett fall in i ett svart hål var en anledning till att jag tyckte den beskrivningen var
intressant.
__________________
2013-02-04
PuffTheDragon har på https://www.flashback.org/sp37376762 en beskrivning av situationen vid ett
svart hål.
Om vi hittar ett svart hål inom räckhåll kommer vi att kunna skicka ett rymdskepp genom det. Vad
händer när skeppet passerar genom hålet?
Antag att det finns två instrument på skeppets instrumentbräda. Det ena är en radiostyrd klocka som
visar tid enligt ett atomur på Jorden och det andra är en avståndsmätare som visar avståndet från
Jorden. Före start är det lätt att se vilket som är avståndsmätare och vilket som är klocka. Klockan
går och avståndsmätaren står stilla. När skeppet tar fart börjar avståndsmätaren att gå och klockan
saktar in.
Skeppet får falla i fritt fall mot hålet. När det når händelsehorisonten har det kommit upp i
ljushastighet. Klockan har stannat men avståndsmätaren går på samma sätt som klockan gjorde
före start. Klocka och avståndsmätare ser alltså ut att ha bytt plats. En av mina rumsaxlar har blivit
skeppets koordinattidsaxel och min koordinattidsaxel har blivit en av skeppets rumsaxlar. Men
frånsett att instrumenten bytt plats märker besättningen ingenting av händelsehorisontpassagen.
Ombord på skeppet fungerar alla naturlagar som vanligt. Skeppets koordinatsystem har vridits i
förhållande till mitt koordinatsystem men det har inte genomgått några inre förändringar. En vanlig
klocka ombord på skeppet går som avståndsmätaren.
När skeppet kommit innanför händelsehorisonten börjar klockan på instrumentbrädan att gå
baklänges och avståndsmätaren saktar in. Skeppet kan nu inte längre kommunicera med Jorden
men för besättningen är allt annat som vanligt. Man fortsätter att skriva i loggboken. Man daterar
loggboken både efter instrumentbrädesklockan, avståndsmätaren och den vanliga klockan.
När skeppet passerat hålets centrum har det rörelseenergi nog att fortsätta ut ur hålet. När det på
nytt passerar händelsehorisonten kan det åter börja rapportera till Jorden. Vi kan då få veta något
om hur det ser ut inne i hålet.
__________________
2013-02-04
Världen i sig har inga koordinater. För att få koordinater som jag kan använda måste jag avbilda
världen på ett koordinatsystem. Vilken typ av koordinater jag då får beror på vilken typ av
koordinatsystem jag valt och vilken typ av avbildning jag använt.
Som jag ser det har jag fyra koordinataxlar varav en pekar mot min framtid. Om vi har en väg som
går mellan gården och handelsboden kan jag och min kompis gå mot handelsboden medan du går
mot gården. Min koordinattidsaxel pekar då mot handelsbodens framtid och din pekar mot gårdens
framtid. Mitt på vägen möts vi och konstaterar att våra framtider ligger mycket nära varandra men
att det finns en liten skillnad som gör att vi kommer att ha ett rumsavstånd när vi kommer fram.
Jag och allt i min närmaste omgivning färdas mot nästan samma framtid. Det innebär att det
vanligtvis är självklart vad som skall vara koordinattidsriktning. Men vad som är koordinattidsriktning
är inte en egenskap hos världen. För ett rymdskepp som passerar mig med en hastighet som ligger
nära ljushastighet kan det som för mig är rum vara koordinattid.
__________________
2013-02-06
Du har helt rätt i att R^4 , R^(3,1) och R^(2,2) alla är fyrdimensionella och alltså kan ta emot en
bijektiv bild av verkligheten. Om information kunde överföras med oändlig hastighet skulle det inte
spela någon roll om man separerade axlarna eller inte. Då kunde man hantera varje koordinat som
oberoende av de övriga. Men om det finns en maximal hastighet blir inte tid och rum alltid
oberoende av varandra. Om jag sänder en signal för att påverka en stjärna som ligger på
rumsavståndet en miljon ljusår tar det två miljoner år innan jag får veta resultatet. Stjärnan är
alltså avlägsen både i tid och rum. Och när man transformerar mellan system som rör sig i
förhållande till varandra får rumskoordinater tidsprojektioner och tvärtom. Frågan är då hur man
hanterar detta.
Om man har separerat en axel som tidsaxel kan man inte direkt vrida in den i rummet för att kunna
projicera rums- och tidskoordinater på varandra. Man behöver använda en icke-ortogonal transform
för att projicera rum och tid på varandra. Den fråga jag en gång i tiden ställde mig var: "Kan jag
inte i stället vrida det ortogonala systemet i R^4?" Det kan jag naturligtvis göra. Världen bryr sig inte
om hur jag avbildar den eller hur jag hanterar dess bild. Frågan är om jag kan tolka en sådan bild
på ett vettigt sätt. Jag har nu använt det här synsättet i några årtionden och inte funnit något som
talar mot det. Men det betyder naturligtvis inte att det är det enda rätta, bara att det ibland är
användbart.
När det gäller kausaliteten så menar jag att vi ibland använder tid som en förändringsparameter
alltså som ett sätt att ordna händelser i löpande följd. Som jag ser det har detta inte direkt med
läge att göra. Det är därför jag ser parametertiden som något annat än koordinattiden. Kausalitet
avgörs alltså av parametertid. Om det finns ett orsaksamband mellan två händelser är den med
lägst parametertid orsak.
När parametertiden går färdas jag längs min koordinattidsaxel. De punkter jag lämnar kallar jag
dåtid, den punkt där jag befinner mig kallar jag nu och de punkter som ligger framför mig kallar jag
framtid. Pelle som far förbi i ett rymdskepp gör likadant med sin koordinattidsaxel. Att det råkar vara
en av mina rumsaxlar är inget som han märker något av.
Om jag vill påverka en händelse på rumsavstånd måste jag skicka en påverkanssignal. Den punkt på
min koordinattidsaxel där jag gör det kallar jag händelsens påverkansnu. Den punkt på min
koordinattidsaxel där jag befinner mig vid den parametertid som händelsen inträffar vid kallar jag
händelsens samtidsnu. Den punkt på min koordinattidsaxel där jag befinner mig där
bekräftelsebilden av händelsen når mig kallar jag händelsens observationsnu. Vid händelsens
påverkansnu och observationsnu är minkowskiavståndet till händelsen noll.
Jag sätter v/c = sin(a) där (a) är min vridningsvinkel. Eftersom sin inte kan bli större än ett behöver
jag då ingen begränsning av vridningsvinkeln. Även vridning mer än 90 grader kan ges en tolkning
vilket kommer att bli aktuellt när vi någon gång i framtiden börjar färdas genom svarta hål.
Lika lite som koordinatsystemet finns i verkligheten finns vridningsvinkeln i verkligheten. Den är en
egenskap hos det koordinatsystem jag valt. Men skall man leta efter en känguru är det kanske där
man skall leta. Men det är inte lätt att hitta genomförbara experiment som kan visa vad som gäller.
För de hastigheter vi normalt hanterar är skillnaden mellan sin och tan inte mätbara.
__________________
2013-02-07
Jag vet inte hur man hanterar bilder men vi kanske återigen kan använda dbshw:s bild
 Den är bra även om en del av texten är irrelevant i det här fallet. (Som jag ser det borde den blå
texten vara "50m/0,99c" och den svarta "kortare än 50m/0,99c")
Jag sätter c lika med ett. Jag använder alltså samma enhet för tid och längd. Vi skall ju tolka bilden,
inte sortomvandla.
Den röda linjen genom A och C är min koordinattidsaxel och koordinattidsaxeln för ladans vänstra
ände. Den röda linjen genom B och D är koordinattidsaxeln för ladans högra ände. Den blå linjen
genom A och D är Pelles koordinattidsaxel. Vinkeln mellan min och Pelles koordinattidsaxlar, alltså
vikeln CAB, är (a).
När Pelle springer in i ladan finns jag , Pelle och ladans vänstra ände i A. Och ladans högra ände
finns i B. När parametertiden går färdas jag och ladans båda ändar längs våra koordinattidsaxlar så
att när Pelle kommer ut ur ladan befinner jag mig i C och ladan ligger längs den streckade linjen CD.
Pelles koordinattid går genom ladan. När han färdas längs sin koordinattidsaxel kommer han alltså
att färdas från ladans ena ände vid A till den andra änden vid D. Den blå linjen mellan A och D är
alltså Pelles koordinattid för loppet. Vi kan kalla beloppet av denna koordinattid för T. Om Pelle har
med sig ett stoppur som han håller i handen mäter stoppuret parametertiden under loppet. Pelle
sätter av stoppurets parametertid som koordinattid på sin koordinattidsaxel. T är alltså
parametertiden för loppet.
Ladans längd, det vill säga den streckade linjen CD, är Tsin(a). Dagen före loppet har vi mätt ladans
längd och enats om hur lång ladan är. Pelle tar nu Tsin(a) och dividerar med T enligt sitt stoppur
och kommer till att hastigheten var Tsin(a)/T = sin(a).
Projektionen av T på min koordinattidsaxel är Tcos(a). Genom att Pelle delvis sprang i min
rumsriktning rörde han sig långsammare i min koordinattidsriktning.
Mot detta kan man invända att Pelle tar ladans längd i mitt koordinatsystem och dividerar med tiden
i sitt koordinatsystem (det vill säga med parametertiden). Då kan man hävda att han skulle i stället
ta Tsin(a)/Tcos(a) = tan(a) alltså ladans längd i mitt koordinatsystem dividerat med T:s projektion
på min koordinattidsaxel. Men ett problem med detta är att punkten C inte motsvarar någon verklig
händelse. Om jag försöker mäta tiden med ett stoppur finns det ingenting som säger att jag skall
trycka på stopp vid C. Bilden av Pelle i ladans utgångsdörr har ännu inte nått mig. När ljuset som
visar att Pelle kommer ut når fram till mig kan jag trycka på stoppuret. Från den tid som stoppuret
då visar kan jag dra bort gångtiden för ljus från D till min koordinattidsaxel och konstatera att jag
borde ha tryckt vid C. Sträckan AC är alltså inte direkt uppmätbar utan bara något som kan beräknas
enligt vissa regler. Det innebär att tan(a) inte är ett invändningsfritt sätt att definiera hastighet.
Jag tror att de flesta människor som fick uppgiften att springa genom ladan med en viss hastighet
skulle göra som Pelle, det vill säga mäta upp ladans längd före loppet, springa genom ladan med ett
stoppur och beräkna hastigheten som den uppmätta längden dividerad med vad stoppuret visar. Det
vill säga Tsin(a)/T = sin(a).
Jag säger inte att det är något fel på minkowskimetriken. Bara att den ibland är otillräcklig och att
det finns andra sätt att beskriva världen.
__________________
2013-02-08
Frågan är: "Vad är en synkron klocka?".
På 1950-talet jobbade jag på Televerkets radiosektion. På den tiden var det aktuellt att navigera
med hjälp av radiofyrar. Så småningom kom stabilare klockor, satelliter och GPS men det gav en
intressant inblick i användning av synkrona klockor.
Jag ställer mig vi ladans vänstra ände med en klocka. Kalle ställer sig vid ladans högra ände med en
klocka. För att synkronisera våra klockor håller jag upp min så att Kalle ser den och kan ställa sin
klocka. Så springer Pelle. Jag noterar klockslaget när han springer in och Kalle noterar klockslaget
när han springer ut. Kalle rapporterar sitt klockslag till mig. Från Kalles klockslag drar jag mitt
klockslag och får en tid som motsvarar AC. Allt verkar fungera.
"Men," säger jag till Kalle "håll för säkerhets skull upp din klocka så att jag kan kontrollera att den
går rätt".
Kalle håller upp klockan och jag säger: "Den går för sakta. Den går fel med 2(50/c)."
"Nej den går exakt lika som din."
"Så här kan vi inte ha det."
"Jag vet. Vi tar två atomur, synkroniserar dem vid A och flyttar ett av dem till D. Vi kan ju låta Pelle
ta med uret. Han skall ju ändå från A till D."
"Men det är ju vad vi gjorde första gången. Pelles stoppur är av yppersta klass. Det går lika stabilt
som ett atomur."
Klockor mäter parametertid. Om vi använder Einsteins definition av längd och tid blir hastighet det
som vi mäter med en meterstav dividerat med det som vi mäter med en klocka alltså längd genom
parametertid.
__________________
2013-02-09
Det finns många synpunkter på synkronisering av klockor. Den artikel som du hänvisar till tar upp
några. Den synkroniseringsmetod du nämner innebär, som jag ser det, att du anser att klockorna
går synkront när de går i varandras samtidsnu. När Kalle och jag ser lika stora fel när vi tittar på
varandras klockor. Och du hävdar att hastighet är inte kvoten mellan det man mäter med en
meterstav dividerat med det man mäter med en klocka utan kvoten mellan det man mäter med en
meterstav och skillnaden mellan det man mäter med två klockor. Så kan man göra men jag vet inte
om det kan ses som helt självklart.
Innan vi i detalj diskuterar tolkning av bilden borde vi väl enas om att den är gjord på rätt sätt. Jag
tror att vi är överens om att om jag har ett läge angivet som tre rumskoordinater och en
tidskoordinat kan jag entydigt lägga in det i ett koordinatsystem enligt bilden. Det betyder att jag kan
lägga in punkterna A , B, C och D. Och det betyder att jag kommer att färdas genom A och C, Pelle
kommer att färdas genom A och D och Kalle genom B och D.
Jag tror att vi är överens fram till frågan om vad som är Pelles tidsaxel. Enligt dig är det inte den blå
linjen utan en axel som ligger mellan AC och AD med vinkeln (b) mot AC sådan att tan(b) = sin(a).
Du menar att om jag transformerar (a) till mitt referenssystem så får jag (b). Är det så?
Din vanliga invändning är att vi behöver inte alls använda den här bilden men som jag ser det är den
så självklar att vi alla, medvetet eller omedvetet, använder den och då kan man inte bara förneka
den. Fysik handlar om att beskriva och tolka upplevelser inklusive vardagsupplevelser.
__________________
2013-02-10
Först en synpunkt på val av referenssystem.
Vinkeln (a) är vinkeln MELLAN mitt och Pelles system. Den hör lika mycket till Pelles som till mitt
system. Den används för överföring mellan systemen. När jag använder (a) går jag alltså från det
ena systemet till det andra. När jag tar Pelles löptid gånger sin(a) innebär användningen av (a) att
jag tar resultatet till ladans längd i mitt system. Det är därför som det intuitivt känns rätt att göra så.
Så tar du upp den fråga som länge har bekymrat mig också. Hur går ljuset från en händelse fram till
mig? Jag vet fortfarande inte hur jag hanterar bilder men du har tydligen liksom jag konstaterat att
det borde gå i 45 grader mot t-axeln. Men då blir ju gångvägen längre än rumsavståndet. Det är här
jag behöver en eter. Om ljuset går vinkelrätt mot färdriktningen i en eter som följer med mig i t-
riktningen blir ljusets gångväg lika med rumsavståndet. Frågan blir då hur man hanterar övergångar
mellan olika referenssystem som alla har en medföljande eter. Men du kan aldrig gå mellan två
referenssystem som har en hastighet i förhållande till varandra utan att passera en
accelerationszon. Frågan blir då hur ljuset går genom en accelerationszon.
__________________
2013-02-14
Visst har ljus partikelegenskaper men inte när det gäller hastighet. Partiklar kan ha olika hastighet
men enligt Maxwells ekvationer är ljusets hastighet i förhållande till det ljusbärande mediet bestämd
av det ljusbärande mediets kapacitans och induktans.
När jag färdas längs min koordinattidsaxel följer ladan, marken där jag står och luften som omger
mig med mig. Det ligger då nära till hands att anta att även det ljusbärande medium som jag svävar
i följer med mig.
__________________
2013-02-17
Maxwells ekvationer kan ses som en generalisering av Kirchhoffs lagar. Kirchhoffs lagar handlar om
källfrihet och virvelfrihet. Maxwell generaliserade sambanden till att handla om källstyrka och
virvelstyrka. Elegant - särskilt om man tänker på att radiovågor var ett okänt begrepp på Maxwells
tid, men det är enkelt och rakt på sak.
Om jag skickar en signal på en telefonledning går den längs ledningen med en hastighet som
bestäms av ledningens kapacitans och induktans. Samma regler gäller om jag skickar en signal på
en glasfibertråd eller genom en glasbit eller genom vakum. Vakum kan alltså fungera som
referenssystem för signalens hastighet.
Om jag spelar biljard ombord på en båt som går med konstant hastighet fungerar biljardbordet som
mitt "utbredningsmedium". Alla lagar som styr bollarnas rörelse kan uttryckas med bordet som
referenssystem. Om jag vet båtens fart och riktning kan jag omvandla hastigheter i förhållande till
bordet till hastigheter i förhållande till omgivande vatten men det är inte dessa hastigheter jag
använder när jag skall beräkna en stöt mot en boll. Det är hastigheter i förhållande till det bord som
följer med mig som är användbara. Och c är en hastighet i förhållande till det medium som följer
med mig.
För partikelhastighet och vågutbredning kan man sätta partikelhastigheten lika med
grupphastigheten för en våg. Det leder till Schrödingerekvationen som man kan se som
telegrafekvationen för ett medium där kapacitans och induktans bestäms av partikelns
rörelseeneergi. Det innebär att man kan se massa som en egenskap hos mediet men det är värt en
egen mässa.
__________________
2013-02-19
Du har rätt i att man kan härleda ett specialfall från ett generellt samband men för att komma från
ett specialfall till ett generellt samband krävs mer än bara härledning. Jag ville bara påpeka att det
inte är något konstigt med Maxwells ekvationer.
Med hjälp av en universell hastighet kan man omvandla tidsenheter till längdenheter eller tvärtom.
Men vilken hastighet är den universella? Vi kan inte säga ljushastigheten eftersom det är uppenbart
att ljushastigheten är olika i olika material. Så vi försöker säga att det är ljushastigheten i vakuum.
Men därav kan vi inte dra slutsatsen att ljushastigheten i vakuum alltid är konstant. Jag menar att vi
måste gå minst ett steg till och säga att det är ljushastigheten i vakuum där det inte finns någon
gravitation. Du kan naturligtvis skriva Maxwells ekvationer för gravitationsfritt vakuum men då måste
du anpassa dem till det medium som du använder dem i.
När det gäller hastighet i 45 grader så är det som jag ser det inte fråga om en hastighet i
förhållande till ett utbredningsmedium och därmed inte ett problem.
Jag tror inte världen bryr sig om hur "man" härleder Schrödingerekvationen. Frågan är hur den kan
tolkas.
__________________
2013-02-21
Maxwells ekvationer är utmärkta verktyg för att hantera signaler i kraftledningar, telefonledningar,
glasfiberkablar, glaslinser, radiolänkar, radarsystem med mera. Jag har mycket sällan använt dem
för signaler i vakuum.
Frågan om universell hastighet är stor men jag skall försöka säga något om hur jag ser på den.
Det tycks finnas en egenskap hos världen att ett kvanta bara kan byta plats med intilliggande
kvantaposition. Jag antar att det är så. Varje gång ett kvanta byter plats med intilliggande
kvantaposition förändras världen. Jag kallar detta för en enhetshändelse och den inkrementerar
parametertiden. Om världen innehåller h kvanta kommer var h:te enhetshändelse att gälla ett visst
kvanta. Detta kvanta kan alltså förflytta sig en kvantaposition på h parametertidsenheter. Om alla
förflyttniingar sker i samma riktning förflyttar det sig då med hastigheten 1/h kvantapositioner per
parametertidsenhet. Detta är den högsta möjliga hastigheten. Jag definierar då hastighet som
förflyttning i ett utbredningsmedium (kvantapositionerna utgör ju ett utbredningsmedium) dividerat
med den parametertid som förflyttningen tar.
Men vi använder inte bara begreppet hastighet i betydelsen förflyttning per tidsenhet utan även i
betydelsen avståndsändring per tidsenhet. Vid till exempel siktesberäkning måste man använda
minst tre olika hastigheter. Hastighet i förhållande till målet, hastighet i förhållande till omgivande
luft och hastighet i förhållande till markkontrollen. Det är enbart hastigheten i förhållande till
omgivande luft som kan ses som förflyttning i utbredningsmediet (luft) dividerad med
parametertiden.
Som jag ser det är varje observatör en del av det medium som omsluter observatören.
__________________
2013-02-23
Jag utgår inte från fysikens beskrivning av världen. För mig är verkligheten den värld som jag
upplever med mina sinnen. I fysikboken hittar jag en beskrivning, alltså en karta över världen. Om
kartan inte stämmer med verkligheten gäller verkligheten. Men oftast stämmer kartan när man väl
lärt sig hur den skall tolkas.
Avbildningar kan göras på olika sätt. Att en avbildning är korrekt betyder inte att alla andra är fel.
Olika korrekta avbildningar kan framhäva olika egenskaper hos föremålet. Det är därför ofta
motiverat att använda flera avbildningar av samma föremål.
Jag säger inte att det är något fel på en avbildning med raka ljusstrålar. Jag säger bara att ibland
visar den inte det jag vill se och då vill jag ha en annan bild. Jag kan avbilda på vilket
koordinatsystem som helst. Världen påverkas inte av mitt sätt att avbilda den. Men när jag använder
bilden måste jag ta hänsyn till hur den är gjord.
Jag kan naturligtvis rita en bild på rutat papper och använda bilden enligt regler som motsvarar de
regler jag använde när jag ritade den.
För ALLA avbildningar gäller att en egenskap hos bilden kan vara en egenskap hos förlagan eller en
egenskap hos avbildningen. Att parallella linjer får V-form i en perspektivbild är inte en egenskap
hos förlagan utan en egenskap hos avbildningen. Trots det är perspektivbilder användbara.
Hela datatekniken bygger på insikten att man kan avbilda på binära tal. Det är en avbildning som har
visat oss en rad nya möjligheter.
Artikeln som du hänvisar till handlar om eventuella olinjariteter vid höga energinivåer. En intressant
fråga men den har mycket lite med val av koordinatsystem att göra.
__________________
2013-02-24
Två system A och B rör sig i förhållande till varandra. En observatör i A och en observatör i B
uppmäter samma ljushastighet i alla riktningar. Den slutsatsen kan man dra av MM:s försök. Det är
då uppenbart att en ljusstråle kan inte gå rakt mellan observatörerna i A och B. Men om man säger
att man bara kan gå mellan A och B via en icke-ortogonal transformation som vrider t-axeln i
förhållande till x-axeln kan man vrida ljusstrålen så att den blir rak.
Så kan man göra.
Ett annat sätt är att säga att man kan inte gå mellan A och B utan att passera en accelerationszon
som kröker ljusstrålar.
__________________
2013-02-24
Vem har sagt att vi pratar fysik? Gud Fader? Jag gör det inte. Jag försöker berätta lite om hur jag
hanterar den värld som omger mig. Och det handlar om olika sätt i olika sammanhang.
Ett exempel på en egenskap hos världen är färg. Jag hanterar färg antingen som ljusvåglängd eller
som RGB-värde med tre bytes per pixel eller som recept på brytfärger. Att ett av sätten ät rätt
betyder inte att de andra är fel. Jag använder alla tre sätten i olika sammanhang.
När det gäller val av koordinatsystem har vi alla en vana vid att använda ett reellt fyrdimensionellt
system. Det är inte så att vi enbart projicerar på ett tredimensionellt rum. Vi är mycket medvetna
om en fjärde koordinat när vi väntar i kön med vår kölapp. För hundra år sedan kompletterade vi
detta system med relativitetsteorins synsätt. Det gjorde att vi kunde se vissa samband tydligare men
det handlade trots allt bara om en liten del av den lilla del av min värld som kallas fysik. I vår vardag
använder vi, även du, vår gamla uppfattning om avstånd i tid och rum.
Men du har rätt i att det är viktigt att man tar reda på hur olika synsätt fungerar och hur de övergår i
varandra.
Hilbert lär ha ansett att Einstein var korkad eftersom han inte nöjde sig med ekvationer utan skulle
ha beskrivningar på vardagsspråk. Ett vanligt Einstein-citat är " Sen matematikerna fick hand om
relativitetsteorin förstår jag den inte själv.". Även om det var skämtsamt ligger det en insikt i det.
Ett matematiskt uttryck kan vara ett effektivt sätt att säga något men om man inte förstår
innebörden är det värdelöst.
__________________
2013-02-26
Det ligger en del i det du säger men det är inte hela sanningen.
Latin och matematik är ibland effektiva språk men en dumhet förblir en dumhet vilket språk man än
formulerar den på. Den insikt som gör att vi ibland kan se att kejsaren är naken måste bygga på
sunt bondförnuft. Hur mycket prästen än säger "Hoc est corpus" måste vi se att han håller en brödbit
i handen. Och hur mycket man än påstår att en krökt ljusstråle är rak i ett krökt rum måste vi se att
den är krökt i förhållande till rummet.
Jag skall försöka att mycket kortfattat antyda hur jag ser på Lorentztransformen.
När jag ser en stjärna är det ljus från stjärnan som når mig. Detta är den enda information om
stjärnan som når mig. Jag kan inte nå den på något annat sätt för att kolla hur ljuset från den har
gått för att komma fram till mig. Jag kan då anta att ljusstrålar är raka. I mitt närområde kan jag
jämföra bilder av föremål med andra sätt att nå dem och även om jag finner många exempel på
krökta ljusstrålar kan jag konstatera att ljusstrålar ofta är raka. Jag kan då använda raka ljusstrålar
som ett axiom och bygga en modell av världen med detta.
Ljus utbreder sig parallellt med mina rumsaxlar, till exempel x-axeln. Antag att jag befinner mig i
system A och ser på system B som rör sig i förhållande till A. Om jag vrider koordinatsystemet i B så
att B:s t-axel bildar en vinkel med min t-axel kommer även B:s x-axel att bilda en vinkel med min x-
axel. Raka ljusstrålar som utbreder sig i system B, alltså parallellt med B:s x-axel, kan då inte vara
parallella med min x-axel. Hur skall man hantera detta?
Som jag ser det finns det åtminstone två sätt. Antingen använder man en icke-ortogonal transform
(Lorentztransformen) som inte bevarar rät vinkel mellan t-axeln och x-axeln eller också låter man
ljusstrålarna krökas så att de når mig parallellt med min x-axel. Båda metoderna ger resultatet att
ljusstrålar i B är parallella med B:s x-axel och i A parallella med A:s x-axel. Vilket sätt man använder
är en fråga om hur man hanterar bilden. Förlagan påverkas inte av vilken metod man använder.
Om man nu använder metoden att arbeta med krökta ljusstrålar kan man naturligtvis "bevisa" att
det blir "fel" eftersom ljusstrålar blir krokiga. Men om man väljer en viss modell måste man
utvärdera den inom sig. Man får bara jämföra modelloberoende resultat.
Jag antar att din invändning är att vi bara behöver ett sätt att se på världen men jag tror att olika
sätt kan visa oss olika möjligheter. Det kan jag ju inte veta men jag tror att chansen är tillräcklig för
att det skall vara mödan värt.
Det här är ingen ny teori. Jag ser ju bara på min värld på det sätt som vi alltid har gjort.
__________________
2013-02-28
Om man släpper kravet att ljusstrålar skall vara raka kan en ljusstråle gå mellan Pelles och min
koordinattidsaxel via en cirkelbåge. En cirkel med centrum i origo är vinkelrät mot alla
koordinattidsaxlar som går genom origo. Om en foton går från (0,x) till (t=x,0) via en cirkelbåge blir
mitt rumsavstånd till fotonen roten ur (x^2 - t^2). Om man släpper förbudet mot att tala om en eter
kan man tillämpa hela strömningsläran på eterflödet och bland annat se gravitation som eterflödets
divergens.
Men det handlar inte om någon ny matematiskt formulerad teori. Bara om att se innebörden i
välkända samband. Jag försöker påpeka att jag bara berättar hur jag använder den världsbild jag
tror att vi alla känner igen. Att vi ibland använder tid som förändringsparameter och ibland som
koordinat och att jag försöker påpeka att vi borde skilja mellan begreppen parametertid och
koordinattid är inte heller någon ny teori, bara ett sätt att undvika en del missförstånd.
__________________
2013-03-05
Jag skall försöka beskriva hur koordinattid och rum fungerar.
När parametertiden går färdas jag med ljushastighet åt något håll i en fyrdimensionell rymd. Jag
lägger in ett fyraxligt, rätlinjigt, ortogonalt koordinatsystem och vrider det så att en av axlarna pekar
i min färdriktning. Den axeln kallar jag koordinattidsaxel eller t-axel. De övriga tre axlarna kallar jag
rumsaxlar eller x- , y-, z-axel. Jag kan alltså per definition aldrig lämna min koordinattidsaxel bara
färdas framåt längs den.
Via ljus som når mig kan jag se föremål på rumsavstånd. Om de färdas med samma hastighet som
jag gör blir deras rumskoordinater oförändrade och jag upplever att jag ligger stilla i rummet. Jag
kan nå en punkt som befinner sig på rumsavstånd genom att jag kan vrida min koordinattidsaxel så
att den pekar in i det som före vridningen var mitt rum. På det sättet kan jag alltså få min
koordinattidsaxel att gå genom punkten så att jag når den när jag färdas längs axeln.
För mig är koordinattiden speciell eftersom det är min färdriktning men för världen är det ingen
skillnad mellan rum och koordinattid. Om jag kunde vrida min koordinattidsaxel 90 grader skulle jag
kunna vrida den till min gamla x-axel som då skulle bli min nya koordinattidsaxel. Om jag kunde
skicka ett rymdskepp längs x-axeln skulle jag kunna beordra dem att uppnå ljushastighet så att
deras koordinattidsaxel blev min x-axel och be dem att berätta hur min koordinattidsaxel ser ut sedd
från sidan som en rumsaxel. Men dels förlorar jag möjligheten att kommunicera med skeppet när
det når ljushastighet dels kommer min koordinattidsaxel att ligga långt bort i deras dåtid.
Funderar man lite på detta blir det enkelt och självklart. Jag ser, som sagt, min hastighetsmätare
som om den visar nanosinus och när jag tar ett metersteg på en sekund känner jag hur
accelerationen vrider min koordinattidsaxel så att jag färdas en meter in i mitt gamla rum medan
jag färdas 300 000 km i koordinattidsled.
__________________
2013-03-07
Som fristående definitioner har jag svårt att få ut något av dem. Men vi är tydligen överens om att
man kan dela upp världen i smådelar. Även om man skulle kunna fortsätta uppdelningen i oändlighet
kan man ju då stanna vid någon nivå som man anser tillräcklig. Kanske redan på Planck-nivå men
jag tror att man bör utgå från Hubble-konstanten.
En koordinat har ingenting med kausalitet att göra. Att Uppsala ligger norr om Stockholm säger
ingenting om vad som är orsak och vad som är verkan. Det är därför som jag försöker påpeka att tid
är en sammanfattning av två olika begrepp. Dels en förändringsparameter (parametertid) dels en
koordinat (koordinattiden).
Parametertiden ordnar händelser i en följd på sådant sätt att en händelse inte kan vara orsak till
föregående händelser.
Koordinattiden anger läge i en fyrdimensionell värld. När parametertiden går ökar min koordinattid
på samma sätt som avståndet från avgångsstationen ökar när jag åker tåg men det betyder inte att
skillnaden mellan begreppen försvinner.
__________________
2013-03-09
Ett kort försök att sammanfatta grunden för mitt sätt att se på min värld.
Min värld är en värld som är tillräckligt stor och uppdelad i tillräcligt små kvanta. Den består av h
kvanta inordnade i H kvantapositioner. h och H är ändliga tal. H är grupperat i fyra dimensioner.
Ett kvanta kan bara ändra läge genom att byta plats med intilliggande tom kvantaposition. När detta
inträffar inträffar den minsta möjliga förändringen av min värld. Jag kallar detta för en
enhetshändelse. Varje gång (every time) en enhetshändelse inträffar inkrementeras en storhet som
jag kallar absolut tid. Absolut tid tilldelar alltså varje enhetshändelse ett unikt nummer. Just nu
anger absolut tid antalet enhetshändelser sedan tidens början (sedan gränsen för min värld). En
händelse kan inte vara orsak till händelser med lägre nummer, alltså lägre absolut tid. Skillnaden
mellan absolut tid för handelse A och händelse B kallar jag parametertiden mellan A och B.
Om jag betraktar ett visst kvanta gäller att det kommer att ändra läge var h:te gång en
enhetshändelse inträffar. Om kvantat enbart omges av tomma kvantapositioner kommer det varje
gång att förflytta sig i samma riktning. Det färdas alltså med hastigheten 1/h kvantapositioner per
enhetshändelse. Färdriktningen kallar jag kvantats koordinattidsriktning och förflyttningen kallar jag
kvantats koordinattid.
Observera att min värld är fyrdimensionell. Jag kan alltså lägga in fyra vinkelräta koordinataxlar x-,
y-, z- och t-axeln. Lägger jag t-axeln i kvantats koordinattidsriktning kommer det att ligga stilla i x-,
y-, och z-led.
Att parametertiden går innebär att händelser, som kan uppdelas i enhetshändelser, inträffar i min
värld. När mitt kvanta ändrar läge, alltså när koordinattiden för mitt kvanta ändras, vet jag att det
inträffat h enhetshändelser i min värld. Jag kan alltså använda mitt kvantas koordinattid som mått på
parametertiden. Om jag anger parametertiden i en enhet som är h enhetshändelser går mitt kvanta
en kvantaposition per parametertidsenhet så att beloppet av kvantats koordinattidsändring och
ändringen av parametertid blir lika. Detta har medfört en del problem när det gäller att se skillnaden
mellan begreppen men samma siffervärde betyder naturligtvis inte att begreppen är identiska.
Parametertid är en förändringsparameter som bland annat anger kausalitet. Koordinattid är en
koordinat som anger läge i en fyrdimensionell värld.
__________________
2013-03-11
Som jag ser det är det uppenbart att vi ibland använder "tid" som en förändringsparameter ibland
som en koordinat. Ett problem med ett sådant samlingsbegrepp är att om jag transformerar
tidskoordinaten transformerar jag även förändringsparametern. Tidskoordinaten blir då inte en
koordinat på samma sätt som rumskoordinaterna utan en storhet som måste särbehandlas.
Hur skall man kunna se tid som ett speciellt begrepp samtidigt som tidskoordinaten kan ha
rumsprojektioner? Minkowski föreslog en elegant lösning: Använd imaginär tid. Den är speciell men
blir reell när man kvadrerar den. Kvadraten kan alltså hanteras som andra koordinatkvadrater.
Ett annat sätt är att se parametertid och koordinattid som två olika begrepp.
Att se parametertid och koordinattid som olika begrepp kräver inte några nya matematiska
hjälpmedel. Det handlar bara om att hålla isär vad som är förändringsparameter och vad som är
koordinat. Och naturligtvis kan man fortfarande transformera dem som ett sammanfattande begrepp
men det viktiga är att man inte behöver göra det. Man kan transformera koordinattid som en
koordinat och parametertid som en parameter.
Den "matematik" som behövs är bara att man använder olika beteckningar för koordinattid och
parametertid. Jag brukar använda t för koordinattid och den grekiska bokstaven tao för
parametertid.
__________________
2013-03-14
Vi har alla gjort oss någon bild av den värld vi lever i. Jag tror att det kunde vara intressant att
utbyta lite erfarenheter av att använda dessa bilder. Därför berättar jag lite om min bild. Den som så
vill kan ju ibland tänka tanken: "Är detta en förändringsparameter eller en koordinat?". Kanske kan
någon se någon ny möjlighet. Bra eller dåligt? Tja det kan man ju inte säga i förväg.
Jag håller med dig om att man bör ta reda på hur den gängse världsbilden ser ut, om inte annat så
för att kunna ifrågasätta den. Och det kan också vara bra att känna till en del matematik. En vacker
dag kanske man behöver Christoffel¨s symboler eller Laplacetransformen och då kan det vara bra
att veta att de finns genomtänkta och färdiga att använda.
Naturligtvis kan man, som med Lorentztransformen, vrida x-axeln mot t-axeln så att de möts vid 45
grader bara man vet vad man gör och vet vad man skall ha resultatet till. Jag försöker bara påpeka
att det är inte det enda möjliga synsättet.
__________________
Den är bra även om en del av texten är irrelevant i det här fallet. (Som jag ser det borde den blå
texten vara "50m/0,99c" och den svarta "kortare än 50m/0,99c")
Jag sätter c lika med ett. Jag använder alltså samma enhet för tid och längd. Vi skall ju tolka bilden,
inte sortomvandla.
Den röda linjen genom A och C är min koordinattidsaxel och koordinattidsaxeln för ladans vänstra
ände. Den röda linjen genom B och D är koordinattidsaxeln för ladans högra ände. Den blå linjen
genom A och D är Pelles koordinattidsaxel. Vinkeln mellan min och Pelles koordinattidsaxlar, alltså
vikeln CAB, är (a).
När Pelle springer in i ladan finns jag , Pelle och ladans vänstra ände i A. Och ladans högra ände
finns i B. När parametertiden går färdas jag och ladans båda ändar längs våra koordinattidsaxlar så
att när Pelle kommer ut ur ladan befinner jag mig i C och ladan ligger längs den streckade linjen CD.
Pelles koordinattid går genom ladan. När han färdas längs sin koordinattidsaxel kommer han alltså
att färdas från ladans ena ände vid A till den andra änden vid D. Den blå linjen mellan A och D är
alltså Pelles koordinattid för loppet. Vi kan kalla beloppet av denna koordinattid för T. Om Pelle har
med sig ett stoppur som han håller i handen mäter stoppuret parametertiden under loppet. Pelle
sätter av stoppurets parametertid som koordinattid på sin koordinattidsaxel. T är alltså
parametertiden för loppet.
Ladans längd, det vill säga den streckade linjen CD, är Tsin(a). Dagen före loppet har vi mätt ladans
längd och enats om hur lång ladan är. Pelle tar nu Tsin(a) och dividerar med T enligt sitt stoppur
och kommer till att hastigheten var Tsin(a)/T = sin(a).
Projektionen av T på min koordinattidsaxel är Tcos(a). Genom att Pelle delvis sprang i min
rumsriktning rörde han sig långsammare i min koordinattidsriktning.
Mot detta kan man invända att Pelle tar ladans längd i mitt koordinatsystem och dividerar med tiden
i sitt koordinatsystem (det vill säga med parametertiden). Då kan man hävda att han skulle i stället
ta Tsin(a)/Tcos(a) = tan(a) alltså ladans längd i mitt koordinatsystem dividerat med T:s projektion
på min koordinattidsaxel. Men ett problem med detta är att punkten C inte motsvarar någon verklig
händelse. Om jag försöker mäta tiden med ett stoppur finns det ingenting som säger att jag skall
trycka på stopp vid C. Bilden av Pelle i ladans utgångsdörr har ännu inte nått mig. När ljuset som
visar att Pelle kommer ut når fram till mig kan jag trycka på stoppuret. Från den tid som stoppuret
då visar kan jag dra bort gångtiden för ljus från D till min koordinattidsaxel och konstatera att jag
borde ha tryckt vid C. Sträckan AC är alltså inte direkt uppmätbar utan bara något som kan beräknas
enligt vissa regler. Det innebär att tan(a) inte är ett invändningsfritt sätt att definiera hastighet.
Jag tror att de flesta människor som fick uppgiften att springa genom ladan med en viss hastighet
skulle göra som Pelle, det vill säga mäta upp ladans längd före loppet, springa genom ladan med ett
stoppur och beräkna hastigheten som den uppmätta längden dividerad med vad stoppuret visar. Det
vill säga Tsin(a)/T = sin(a).
Jag säger inte att det är något fel på minkowskimetriken. Bara att den ibland är otillräcklig och att
det finns andra sätt att beskriva världen.
__________________
2013-02-08
Frågan är: "Vad är en synkron klocka?".
På 1950-talet jobbade jag på Televerkets radiosektion. På den tiden var det aktuellt att navigera
med hjälp av radiofyrar. Så småningom kom stabilare klockor, satelliter och GPS men det gav en
intressant inblick i användning av synkrona klockor.
Jag ställer mig vi ladans vänstra ände med en klocka. Kalle ställer sig vid ladans högra ände med en
klocka. För att synkronisera våra klockor håller jag upp min så att Kalle ser den och kan ställa sin
klocka. Så springer Pelle. Jag noterar klockslaget när han springer in och Kalle noterar klockslaget
när han springer ut. Kalle rapporterar sitt klockslag till mig. Från Kalles klockslag drar jag mitt
klockslag och får en tid som motsvarar AC. Allt verkar fungera.
"Men," säger jag till Kalle "håll för säkerhets skull upp din klocka så att jag kan kontrollera att den
går rätt".
Kalle håller upp klockan och jag säger: "Den går för sakta. Den går fel med 2(50/c)."
"Nej den går exakt lika som din."
"Så här kan vi inte ha det."
"Jag vet. Vi tar två atomur, synkroniserar dem vid A och flyttar ett av dem till D. Vi kan ju låta Pelle
ta med uret. Han skall ju ändå från A till D."
"Men det är ju vad vi gjorde första gången. Pelles stoppur är av yppersta klass. Det går lika stabilt
som ett atomur."
Klockor mäter parametertid. Om vi använder Einsteins definition av längd och tid blir hastighet det
som vi mäter med en meterstav dividerat med det som vi mäter med en klocka alltså längd genom
parametertid.
__________________
2013-02-09
Det finns många synpunkter på synkronisering av klockor. Den artikel som du hänvisar till tar upp
några. Den synkroniseringsmetod du nämner innebär, som jag ser det, att du anser att klockorna
går synkront när de går i varandras samtidsnu. När Kalle och jag ser lika stora fel när vi tittar på
varandras klockor. Och du hävdar att hastighet är inte kvoten mellan det man mäter med en
meterstav dividerat med det man mäter med en klocka utan kvoten mellan det man mäter med en
meterstav och skillnaden mellan det man mäter med två klockor. Så kan man göra men jag vet inte
om det kan ses som helt självklart.
Innan vi i detalj diskuterar tolkning av bilden borde vi väl enas om att den är gjord på rätt sätt. Jag
tror att vi är överens om att om jag har ett läge angivet som tre rumskoordinater och en
tidskoordinat kan jag entydigt lägga in det i ett koordinatsystem enligt bilden. Det betyder att jag kan
lägga in punkterna A , B, C och D. Och det betyder att jag kommer att färdas genom A och C, Pelle
kommer att färdas genom A och D och Kalle genom B och D.
Jag tror att vi är överens fram till frågan om vad som är Pelles tidsaxel. Enligt dig är det inte den blå
linjen utan en axel som ligger mellan AC och AD med vinkeln (b) mot AC sådan att tan(b) = sin(a).
Du menar att om jag transformerar (a) till mitt referenssystem så får jag (b). Är det så?
Din vanliga invändning är att vi behöver inte alls använda den här bilden men som jag ser det är den
så självklar att vi alla, medvetet eller omedvetet, använder den och då kan man inte bara förneka
den. Fysik handlar om att beskriva och tolka upplevelser inklusive vardagsupplevelser.
__________________
2013-02-10
Först en synpunkt på val av referenssystem.
Vinkeln (a) är vinkeln MELLAN mitt och Pelles system. Den hör lika mycket till Pelles som till mitt
system. Den används för överföring mellan systemen. När jag använder (a) går jag alltså från det
ena systemet till det andra. När jag tar Pelles löptid gånger sin(a) innebär användningen av (a) att
jag tar resultatet till ladans längd i mitt system. Det är därför som det intuitivt känns rätt att göra så.
Så tar du upp den fråga som länge har bekymrat mig också. Hur går ljuset från en händelse fram till
mig? Jag vet fortfarande inte hur jag hanterar bilder men du har tydligen liksom jag konstaterat att
det borde gå i 45 grader mot t-axeln. Men då blir ju gångvägen längre än rumsavståndet. Det är här
jag behöver en eter. Om ljuset går vinkelrätt mot färdriktningen i en eter som följer med mig i t-
riktningen blir ljusets gångväg lika med rumsavståndet. Frågan blir då hur man hanterar övergångar
mellan olika referenssystem som alla har en medföljande eter. Men du kan aldrig gå mellan två
referenssystem som har en hastighet i förhållande till varandra utan att passera en
accelerationszon. Frågan blir då hur ljuset går genom en accelerationszon.
__________________
2013-02-14
Visst har ljus partikelegenskaper men inte när det gäller hastighet. Partiklar kan ha olika hastighet
men enligt Maxwells ekvationer är ljusets hastighet i förhållande till det ljusbärande mediet bestämd
av det ljusbärande mediets kapacitans och induktans.
När jag färdas längs min koordinattidsaxel följer ladan, marken där jag står och luften som omger
mig med mig. Det ligger då nära till hands att anta att även det ljusbärande medium som jag svävar
i följer med mig.
__________________
2013-02-17
Maxwells ekvationer kan ses som en generalisering av Kirchhoffs lagar. Kirchhoffs lagar handlar om
källfrihet och virvelfrihet. Maxwell generaliserade sambanden till att handla om källstyrka och
virvelstyrka. Elegant - särskilt om man tänker på att radiovågor var ett okänt begrepp på Maxwells
tid, men det är enkelt och rakt på sak.
Om jag skickar en signal på en telefonledning går den längs ledningen med en hastighet som
bestäms av ledningens kapacitans och induktans. Samma regler gäller om jag skickar en signal på
en glasfibertråd eller genom en glasbit eller genom vakum. Vakum kan alltså fungera som
referenssystem för signalens hastighet.
Om jag spelar biljard ombord på en båt som går med konstant hastighet fungerar biljardbordet som
mitt "utbredningsmedium". Alla lagar som styr bollarnas rörelse kan uttryckas med bordet som
referenssystem. Om jag vet båtens fart och riktning kan jag omvandla hastigheter i förhållande till
bordet till hastigheter i förhållande till omgivande vatten men det är inte dessa hastigheter jag
använder när jag skall beräkna en stöt mot en boll. Det är hastigheter i förhållande till det bord som
följer med mig som är användbara. Och c är en hastighet i förhållande till det medium som följer
med mig.
För partikelhastighet och vågutbredning kan man sätta partikelhastigheten lika med
grupphastigheten för en våg. Det leder till Schrödingerekvationen som man kan se som
telegrafekvationen för ett medium där kapacitans och induktans bestäms av partikelns
rörelseeneergi. Det innebär att man kan se massa som en egenskap hos mediet men det är värt en
egen mässa.
__________________
2013-02-19
Du har rätt i att man kan härleda ett specialfall från ett generellt samband men för att komma från
ett specialfall till ett generellt samband krävs mer än bara härledning. Jag ville bara påpeka att det
inte är något konstigt med Maxwells ekvationer.
Med hjälp av en universell hastighet kan man omvandla tidsenheter till längdenheter eller tvärtom.
Men vilken hastighet är den universella? Vi kan inte säga ljushastigheten eftersom det är uppenbart
att ljushastigheten är olika i olika material. Så vi försöker säga att det är ljushastigheten i vakuum.
Men därav kan vi inte dra slutsatsen att ljushastigheten i vakuum alltid är konstant. Jag menar att vi
måste gå minst ett steg till och säga att det är ljushastigheten i vakuum där det inte finns någon
gravitation. Du kan naturligtvis skriva Maxwells ekvationer för gravitationsfritt vakuum men då måste
du anpassa dem till det medium som du använder dem i.
När det gäller hastighet i 45 grader så är det som jag ser det inte fråga om en hastighet i
förhållande till ett utbredningsmedium och därmed inte ett problem.
Jag tror inte världen bryr sig om hur "man" härleder Schrödingerekvationen. Frågan är hur den kan
tolkas.
__________________
2013-02-21
Maxwells ekvationer är utmärkta verktyg för att hantera signaler i kraftledningar, telefonledningar,
glasfiberkablar, glaslinser, radiolänkar, radarsystem med mera. Jag har mycket sällan använt dem
för signaler i vakuum.
Frågan om universell hastighet är stor men jag skall försöka säga något om hur jag ser på den.
Det tycks finnas en egenskap hos världen att ett kvanta bara kan byta plats med intilliggande
kvantaposition. Jag antar att det är så. Varje gång ett kvanta byter plats med intilliggande
kvantaposition förändras världen. Jag kallar detta för en enhetshändelse och den inkrementerar
parametertiden. Om världen innehåller h kvanta kommer var h:te enhetshändelse att gälla ett visst
kvanta. Detta kvanta kan alltså förflytta sig en kvantaposition på h parametertidsenheter. Om alla
förflyttniingar sker i samma riktning förflyttar det sig då med hastigheten 1/h kvantapositioner per
parametertidsenhet. Detta är den högsta möjliga hastigheten. Jag definierar då hastighet som
förflyttning i ett utbredningsmedium (kvantapositionerna utgör ju ett utbredningsmedium) dividerat
med den parametertid som förflyttningen tar.
Men vi använder inte bara begreppet hastighet i betydelsen förflyttning per tidsenhet utan även i
betydelsen avståndsändring per tidsenhet. Vid till exempel siktesberäkning måste man använda
minst tre olika hastigheter. Hastighet i förhållande till målet, hastighet i förhållande till omgivande
luft och hastighet i förhållande till markkontrollen. Det är enbart hastigheten i förhållande till
omgivande luft som kan ses som förflyttning i utbredningsmediet (luft) dividerad med
parametertiden.
Som jag ser det är varje observatör en del av det medium som omsluter observatören.
__________________
2013-02-23
Jag utgår inte från fysikens beskrivning av världen. För mig är verkligheten den värld som jag
upplever med mina sinnen. I fysikboken hittar jag en beskrivning, alltså en karta över världen. Om
kartan inte stämmer med verkligheten gäller verkligheten. Men oftast stämmer kartan när man väl
lärt sig hur den skall tolkas.
Avbildningar kan göras på olika sätt. Att en avbildning är korrekt betyder inte att alla andra är fel.
Olika korrekta avbildningar kan framhäva olika egenskaper hos föremålet. Det är därför ofta
motiverat att använda flera avbildningar av samma föremål.
Jag säger inte att det är något fel på en avbildning med raka ljusstrålar. Jag säger bara att ibland
visar den inte det jag vill se och då vill jag ha en annan bild. Jag kan avbilda på vilket
koordinatsystem som helst. Världen påverkas inte av mitt sätt att avbilda den. Men när jag använder
bilden måste jag ta hänsyn till hur den är gjord.
Jag kan naturligtvis rita en bild på rutat papper och använda bilden enligt regler som motsvarar de
regler jag använde när jag ritade den.
För ALLA avbildningar gäller att en egenskap hos bilden kan vara en egenskap hos förlagan eller en
egenskap hos avbildningen. Att parallella linjer får V-form i en perspektivbild är inte en egenskap
hos förlagan utan en egenskap hos avbildningen. Trots det är perspektivbilder användbara.
Hela datatekniken bygger på insikten att man kan avbilda på binära tal. Det är en avbildning som har
visat oss en rad nya möjligheter.
Artikeln som du hänvisar till handlar om eventuella olinjariteter vid höga energinivåer. En intressant
fråga men den har mycket lite med val av koordinatsystem att göra.
__________________
2013-02-24
Två system A och B rör sig i förhållande till varandra. En observatör i A och en observatör i B
uppmäter samma ljushastighet i alla riktningar. Den slutsatsen kan man dra av MM:s försök. Det är
då uppenbart att en ljusstråle kan inte gå rakt mellan observatörerna i A och B. Men om man säger
att man bara kan gå mellan A och B via en icke-ortogonal transformation som vrider t-axeln i
förhållande till x-axeln kan man vrida ljusstrålen så att den blir rak.
Så kan man göra.
Ett annat sätt är att säga att man kan inte gå mellan A och B utan att passera en accelerationszon
som kröker ljusstrålar.
__________________
2013-02-24
Vem har sagt att vi pratar fysik? Gud Fader? Jag gör det inte. Jag försöker berätta lite om hur jag
hanterar den värld som omger mig. Och det handlar om olika sätt i olika sammanhang.
Ett exempel på en egenskap hos världen är färg. Jag hanterar färg antingen som ljusvåglängd eller
som RGB-värde med tre bytes per pixel eller som recept på brytfärger. Att ett av sätten ät rätt
betyder inte att de andra är fel. Jag använder alla tre sätten i olika sammanhang.
När det gäller val av koordinatsystem har vi alla en vana vid att använda ett reellt fyrdimensionellt
system. Det är inte så att vi enbart projicerar på ett tredimensionellt rum. Vi är mycket medvetna
om en fjärde koordinat när vi väntar i kön med vår kölapp. För hundra år sedan kompletterade vi
detta system med relativitetsteorins synsätt. Det gjorde att vi kunde se vissa samband tydligare men
det handlade trots allt bara om en liten del av den lilla del av min värld som kallas fysik. I vår vardag
använder vi, även du, vår gamla uppfattning om avstånd i tid och rum.
Men du har rätt i att det är viktigt att man tar reda på hur olika synsätt fungerar och hur de övergår i
varandra.
Hilbert lär ha ansett att Einstein var korkad eftersom han inte nöjde sig med ekvationer utan skulle
ha beskrivningar på vardagsspråk. Ett vanligt Einstein-citat är " Sen matematikerna fick hand om
relativitetsteorin förstår jag den inte själv.". Även om det var skämtsamt ligger det en insikt i det.
Ett matematiskt uttryck kan vara ett effektivt sätt att säga något men om man inte förstår
innebörden är det värdelöst.
__________________
2013-02-26
Det ligger en del i det du säger men det är inte hela sanningen.
Latin och matematik är ibland effektiva språk men en dumhet förblir en dumhet vilket språk man än
formulerar den på. Den insikt som gör att vi ibland kan se att kejsaren är naken måste bygga på
sunt bondförnuft. Hur mycket prästen än säger "Hoc est corpus" måste vi se att han håller en brödbit
i handen. Och hur mycket man än påstår att en krökt ljusstråle är rak i ett krökt rum måste vi se att
den är krökt i förhållande till rummet.
Jag skall försöka att mycket kortfattat antyda hur jag ser på Lorentztransformen.
När jag ser en stjärna är det ljus från stjärnan som når mig. Detta är den enda information om
stjärnan som når mig. Jag kan inte nå den på något annat sätt för att kolla hur ljuset från den har
gått för att komma fram till mig. Jag kan då anta att ljusstrålar är raka. I mitt närområde kan jag
jämföra bilder av föremål med andra sätt att nå dem och även om jag finner många exempel på
krökta ljusstrålar kan jag konstatera att ljusstrålar ofta är raka. Jag kan då använda raka ljusstrålar
som ett axiom och bygga en modell av världen med detta.
Ljus utbreder sig parallellt med mina rumsaxlar, till exempel x-axeln. Antag att jag befinner mig i
system A och ser på system B som rör sig i förhållande till A. Om jag vrider koordinatsystemet i B så
att B:s t-axel bildar en vinkel med min t-axel kommer även B:s x-axel att bilda en vinkel med min x-
axel. Raka ljusstrålar som utbreder sig i system B, alltså parallellt med B:s x-axel, kan då inte vara
parallella med min x-axel. Hur skall man hantera detta?
Som jag ser det finns det åtminstone två sätt. Antingen använder man en icke-ortogonal transform
(Lorentztransformen) som inte bevarar rät vinkel mellan t-axeln och x-axeln eller också låter man
ljusstrålarna krökas så att de når mig parallellt med min x-axel. Båda metoderna ger resultatet att
ljusstrålar i B är parallella med B:s x-axel och i A parallella med A:s x-axel. Vilket sätt man använder
är en fråga om hur man hanterar bilden. Förlagan påverkas inte av vilken metod man använder.
Om man nu använder metoden att arbeta med krökta ljusstrålar kan man naturligtvis "bevisa" att
det blir "fel" eftersom ljusstrålar blir krokiga. Men om man väljer en viss modell måste man
utvärdera den inom sig. Man får bara jämföra modelloberoende resultat.
Jag antar att din invändning är att vi bara behöver ett sätt att se på världen men jag tror att olika
sätt kan visa oss olika möjligheter. Det kan jag ju inte veta men jag tror att chansen är tillräcklig för
att det skall vara mödan värt.
Det här är ingen ny teori. Jag ser ju bara på min värld på det sätt som vi alltid har gjort.
__________________
2013-02-28
Om man släpper kravet att ljusstrålar skall vara raka kan en ljusstråle gå mellan Pelles och min
koordinattidsaxel via en cirkelbåge. En cirkel med centrum i origo är vinkelrät mot alla
koordinattidsaxlar som går genom origo. Om en foton går från (0,x) till (t=x,0) via en cirkelbåge blir
mitt rumsavstånd till fotonen roten ur (x^2 - t^2). Om man släpper förbudet mot att tala om en eter
kan man tillämpa hela strömningsläran på eterflödet och bland annat se gravitation som eterflödets
divergens.
Men det handlar inte om någon ny matematiskt formulerad teori. Bara om att se innebörden i
välkända samband. Jag försöker påpeka att jag bara berättar hur jag använder den världsbild jag
tror att vi alla känner igen. Att vi ibland använder tid som förändringsparameter och ibland som
koordinat och att jag försöker påpeka att vi borde skilja mellan begreppen parametertid och
koordinattid är inte heller någon ny teori, bara ett sätt att undvika en del missförstånd.
__________________
2013-03-05
Jag skall försöka beskriva hur koordinattid och rum fungerar.
När parametertiden går färdas jag med ljushastighet åt något håll i en fyrdimensionell rymd. Jag
lägger in ett fyraxligt, rätlinjigt, ortogonalt koordinatsystem och vrider det så att en av axlarna pekar
i min färdriktning. Den axeln kallar jag koordinattidsaxel eller t-axel. De övriga tre axlarna kallar jag
rumsaxlar eller x- , y-, z-axel. Jag kan alltså per definition aldrig lämna min koordinattidsaxel bara
färdas framåt längs den.
Via ljus som når mig kan jag se föremål på rumsavstånd. Om de färdas med samma hastighet som
jag gör blir deras rumskoordinater oförändrade och jag upplever att jag ligger stilla i rummet. Jag
kan nå en punkt som befinner sig på rumsavstånd genom att jag kan vrida min koordinattidsaxel så
att den pekar in i det som före vridningen var mitt rum. På det sättet kan jag alltså få min
koordinattidsaxel att gå genom punkten så att jag når den när jag färdas längs axeln.
För mig är koordinattiden speciell eftersom det är min färdriktning men för världen är det ingen
skillnad mellan rum och koordinattid. Om jag kunde vrida min koordinattidsaxel 90 grader skulle jag
kunna vrida den till min gamla x-axel som då skulle bli min nya koordinattidsaxel. Om jag kunde
skicka ett rymdskepp längs x-axeln skulle jag kunna beordra dem att uppnå ljushastighet så att
deras koordinattidsaxel blev min x-axel och be dem att berätta hur min koordinattidsaxel ser ut sedd
från sidan som en rumsaxel. Men dels förlorar jag möjligheten att kommunicera med skeppet när
det når ljushastighet dels kommer min koordinattidsaxel att ligga långt bort i deras dåtid.
Funderar man lite på detta blir det enkelt och självklart. Jag ser, som sagt, min hastighetsmätare
som om den visar nanosinus och när jag tar ett metersteg på en sekund känner jag hur
accelerationen vrider min koordinattidsaxel så att jag färdas en meter in i mitt gamla rum medan
jag färdas 300 000 km i koordinattidsled.
__________________
2013-03-07
Som fristående definitioner har jag svårt att få ut något av dem. Men vi är tydligen överens om att
man kan dela upp världen i smådelar. Även om man skulle kunna fortsätta uppdelningen i oändlighet
kan man ju då stanna vid någon nivå som man anser tillräcklig. Kanske redan på Planck-nivå men
jag tror att man bör utgå från Hubble-konstanten.
En koordinat har ingenting med kausalitet att göra. Att Uppsala ligger norr om Stockholm säger
ingenting om vad som är orsak och vad som är verkan. Det är därför som jag försöker påpeka att tid
är en sammanfattning av två olika begrepp. Dels en förändringsparameter (parametertid) dels en
koordinat (koordinattiden).
Parametertiden ordnar händelser i en följd på sådant sätt att en händelse inte kan vara orsak till
föregående händelser.
Koordinattiden anger läge i en fyrdimensionell värld. När parametertiden går ökar min koordinattid
på samma sätt som avståndet från avgångsstationen ökar när jag åker tåg men det betyder inte att
skillnaden mellan begreppen försvinner.
__________________
2013-03-09
Ett kort försök att sammanfatta grunden för mitt sätt att se på min värld.
Min värld är en värld som är tillräckligt stor och uppdelad i tillräcligt små kvanta. Den består av h
kvanta inordnade i H kvantapositioner. h och H är ändliga tal. H är grupperat i fyra dimensioner.
Ett kvanta kan bara ändra läge genom att byta plats med intilliggande tom kvantaposition. När detta
inträffar inträffar den minsta möjliga förändringen av min värld. Jag kallar detta för en
enhetshändelse. Varje gång (every time) en enhetshändelse inträffar inkrementeras en storhet som
jag kallar absolut tid. Absolut tid tilldelar alltså varje enhetshändelse ett unikt nummer. Just nu
anger absolut tid antalet enhetshändelser sedan tidens början (sedan gränsen för min värld). En
händelse kan inte vara orsak till händelser med lägre nummer, alltså lägre absolut tid. Skillnaden
mellan absolut tid för handelse A och händelse B kallar jag parametertiden mellan A och B.
Om jag betraktar ett visst kvanta gäller att det kommer att ändra läge var h:te gång en
enhetshändelse inträffar. Om kvantat enbart omges av tomma kvantapositioner kommer det varje
gång att förflytta sig i samma riktning. Det färdas alltså med hastigheten 1/h kvantapositioner per
enhetshändelse. Färdriktningen kallar jag kvantats koordinattidsriktning och förflyttningen kallar jag
kvantats koordinattid.
Observera att min värld är fyrdimensionell. Jag kan alltså lägga in fyra vinkelräta koordinataxlar x-,
y-, z- och t-axeln. Lägger jag t-axeln i kvantats koordinattidsriktning kommer det att ligga stilla i x-,
y-, och z-led.
Att parametertiden går innebär att händelser, som kan uppdelas i enhetshändelser, inträffar i min
värld. När mitt kvanta ändrar läge, alltså när koordinattiden för mitt kvanta ändras, vet jag att det
inträffat h enhetshändelser i min värld. Jag kan alltså använda mitt kvantas koordinattid som mått på
parametertiden. Om jag anger parametertiden i en enhet som är h enhetshändelser går mitt kvanta
en kvantaposition per parametertidsenhet så att beloppet av kvantats koordinattidsändring och
ändringen av parametertid blir lika. Detta har medfört en del problem när det gäller att se skillnaden
mellan begreppen men samma siffervärde betyder naturligtvis inte att begreppen är identiska.
Parametertid är en förändringsparameter som bland annat anger kausalitet. Koordinattid är en
koordinat som anger läge i en fyrdimensionell värld.
__________________
2013-03-11
Som jag ser det är det uppenbart att vi ibland använder "tid" som en förändringsparameter ibland
som en koordinat. Ett problem med ett sådant samlingsbegrepp är att om jag transformerar
tidskoordinaten transformerar jag även förändringsparametern. Tidskoordinaten blir då inte en
koordinat på samma sätt som rumskoordinaterna utan en storhet som måste särbehandlas.
Hur skall man kunna se tid som ett speciellt begrepp samtidigt som tidskoordinaten kan ha
rumsprojektioner? Minkowski föreslog en elegant lösning: Använd imaginär tid. Den är speciell men
blir reell när man kvadrerar den. Kvadraten kan alltså hanteras som andra koordinatkvadrater.
Ett annat sätt är att se parametertid och koordinattid som två olika begrepp.
Att se parametertid och koordinattid som olika begrepp kräver inte några nya matematiska
hjälpmedel. Det handlar bara om att hålla isär vad som är förändringsparameter och vad som är
koordinat. Och naturligtvis kan man fortfarande transformera dem som ett sammanfattande begrepp
men det viktiga är att man inte behöver göra det. Man kan transformera koordinattid som en
koordinat och parametertid som en parameter.
Den "matematik" som behövs är bara att man använder olika beteckningar för koordinattid och
parametertid. Jag brukar använda t för koordinattid och den grekiska bokstaven tao för
parametertid.
__________________
2013-03-14
Vi har alla gjort oss någon bild av den värld vi lever i. Jag tror att det kunde vara intressant att
utbyta lite erfarenheter av att använda dessa bilder. Därför berättar jag lite om min bild. Den som så
vill kan ju ibland tänka tanken: "Är detta en förändringsparameter eller en koordinat?". Kanske kan
någon se någon ny möjlighet. Bra eller dåligt? Tja det kan man ju inte säga i förväg.
Jag håller med dig om att man bör ta reda på hur den gängse världsbilden ser ut, om inte annat så
för att kunna ifrågasätta den. Och det kan också vara bra att känna till en del matematik. En vacker
dag kanske man behöver Christoffel¨s symboler eller Laplacetransformen och då kan det vara bra
att veta att de finns genomtänkta och färdiga att använda.
Naturligtvis kan man, som med Lorentztransformen, vrida x-axeln mot t-axeln så att de möts vid 45
grader bara man vet vad man gör och vet vad man skall ha resultatet till. Jag försöker bara påpeka
att det är inte det enda möjliga synsättet.
__________________
 Vi försöker igen.
Jag använder din figur. Som jag ser det är den blå linjen Pelles t-axel. Längden i den blå riktningen
är alltså vad Pelles stoppur visar för Pelle. Han springer nu så att den blå sträckan som du angett
som "längre än 50 m/0,99c" blir 50/0,99c. Den röda sträckan som du angett som "50 m/0,99c" är
min tolkning av Kalles signal vilken alltså är mindre än 50/0,99c. Genom att Pelle delvis springer i
mitt rum rör han sig långsammare i min koordinattidsriktning (t-riktning).
Minkowskimetriken bygger på tanken att det finns ett tidsavstånd som kan uppväga ett rumsavstånd
så att resultatet blir noll. Om tidsavståndet är lika med rumsavståndet blir Minkowskiavståndet noll.
Detta fungerar i många fall eftersom vi upplever bilden av en händelse som om den var händelsen.
Vi är tydligen överens om att två punkter med Minkowskiavståndet noll kan ha ett reellt avstånd.
Som jag ser det betyder det att man även måste hålla reda på det reella avståndet vilket
Minkowskimetriken inte gör. Som jag ser det kan Minkowskimetriken komplettera den reella
metriken men inte ersätta den.
__________________
2013-01-14
Om jag ser en stjärna explodera säger jag: "Nu exploderade stjärnan."
Så tänker jag efter och ändrar det till: "Nu blev minkowskiavståndet till stjärnexplosionen noll. Hur
skall jag lägga in det i mitt koordinatsystem?"
Om stjärnan ligger en miljon ljusår bort och om det hade funnits en enorm klocka på stjärnan som
jag kunde se skulle jag se att klockan visade en tidpunkt för en miljon år sedan. Jag ritar då ett
koordinatsystem med en t-axel och en x-axel och med mig i origo. Så lägger jag in
stjärnexplosionen vid t lika med minus en miljon år och x lika med en miljon ljusår.
Stjärnexplosionens koordinattid i mitt system blir alltså minus en miljon år. Sedan dess har
parametertiden gått och jag ha färdats längs min t-axel så att jag nu kommit till origo. Och bilden av
stjärnexplosionen har färdats längs min x-axel så att den nu nått origo där jag kan se den. Från
origo är avståndet i t-riktningen lika stort som avståndet i x-riktningen vilket innebär att
minkowskiavståndet är noll.
Jag tror att detta är ett mycket vanligt sätt att se situationen.
__________________
2013-01-15
Det är mycket möjligt att man inte behöver något annat avståndsbegrepp i relativitetsteori. Men
relativitetsteori är inte hela världen. Den har funnits i cirka hundra år men den reella metriken har vi
använt i många tusen år. Jag tar inte ett steg utan en mängd avståndsbedömningar till väggar. golv.
möbler med mera.
Du har sagt någon gång att man kan bortse från relativitetsteori i vardagen. Att man alltså kan se
relativitetsteori som en spekulation fristående från vardagens verklighet. Så var det kanske för
hundra år sedan men det har hänt en del sedan dess. Vi möter idag en hel del fenomen där
ljushastigheten spelar en viktig roll.
Hela radartekniken bygger på att rumsavståndet är lika med tidsavståndet när minkowskiavståndet
är noll. I GPS använder vi skillnader i koordinattid mellan reellt synkrona klockor placerade i sateliter
med kända lägen. Vi bygger allt större växelströmsnät med mimkowskisynkronism. När jag bygger
ett kretskort för att hantera datorpulser måste jag tänka på att en nanosekundpuls inte är längre än
en fot. När jag ringer till Australien får jag ibland en fördröjning som kräver en viss samtalsdisiplin.
Vi är på väg mot rymdfärder över avstånd där skillnaden mellan parametertid och koordinattid
spelar stor roll.
Allt oftare dyker de samband som ursprungligen härleddes via relativitetsteori upp i andra
sammanhang och med annan härledning. Som jag ser det är det viktigt att ha någon uppfattning om
hur olika synsätt hänger samman.
Minkowskimetriken är inte en egenskap hos verkligheten. Den är en transform som skapats via en
transformationsregel. När jag fotograferade med negativ färgfilm fick jag en en bild där färgerna
transformerats via en transformationsregel. Men eftersom denna regel var bijektiv kunde man vända
på regeln och kopiera bilderna tillbaka till förlagans färger. På samma sätt transformerar man till
minkowskimetriken via en transformationsregel. Men genom att man låser ett samband mellan
tidsavstånd och rumsavstånd blir denna transform inte bijektiv. Det går alltså inte att från
minkowskimetrikens bild bestämma reella avstånd. Minkowskimetriken kan därför bara komplettera
den reella metriken, inte ersätta den.
Det är inte något fel i att använda transformer. Laplace-transformer är mycket användbara inom
reglerteknik, Fourier-transformer är utmärkta när man bygger förstärkare och minkowskimetriken
har ett klart tillämpningsområde. Men en transform är aldrig det enda möjliga synsättet.
Det finns en egendomlig inställning att alla måste se allt på samma sätt. Så är det inte. Det är
genom att vi ser saker på olika sätt som vi kan hitta nya möjligheter. Men då behöver vi tala om för
varandra vad vi ser och naturligtvis måste vi vara öppna för att anpassa vårt synsätt så att det
stämmer med de fenomen som vi observerar.
__________________
2013-01-17
Det reella avståndet till en händelse är roten ur (x^2+y^2+z^2+tc^2).
En händelse kan orsaka en bild som med hastigheten c utbreder sig i alla riktningar. Avståndet till
händelsens bild ärroten ur ( x^2+y^2+z^2-tc^2). Minkowskiavståndet till en händelse är alltså
avståndet till händelsens bild. Eftersom mottagandet av händelsens bild är mitt enda sätt att få veta
något om händelsen kan jag i många fall ersätta händelsen med händelsens bild.
Världen påverkas inte av mitt sätt att avbilda den. Jag kan välja om jag vill avbilda på ett
koordinatsystem med raka eller krokiga, reella eller imaginära axlar. En bild av världen avbildar även
alla fenomen som vi observerat. Det kan vara lämpligt att välja en avbildning som ger en lättanvänd
beskrivning av världen inklusive dess fenomen. Även om jag inte lyckats beskriva det tillräckligt
tydligt har jag försökt tala om att jag använder ett fyrdimensionellt koordinatsystem med raka
ortogonala reella axlar. Om jag i detta beskriver rumshastighet som en vridning av
koordinattidsaxeln så att rumshastigheten blir lika med c gånger sinus för vridningsvinkeln får jag
enkla uttryck för längdkontraktionen och tidsdilationen.
Varje gång en detekterbar händelse inträffar någon stans i universum förändras det och
parametertiden inkrementeras. Parametertid är alltså antalet minsta detekterbara händelser i
universum. Ett antal är en skalär storhet. Varje förändring av universum innebär att mitt läge i
förhållande till mitt omgivande universum förändras. Det lägger jag in i mitt koordinatsystem som att
jag flyttar mig en tidsenhet lika med c längdenheter längs min koordinattidsaxel när parametertiden
ökar med en tidsenhet.
En klocka räknar antalet händelser i ett tidsgivande element. Eftersom det tidsgivande elementet är
en viss andel av hela universum blir detta ett mått på antalet händelser i hela universum. En klocka
mäter alltså parametertid.
Om det vid en händelse finns en klocka kommer bilden av klockan att följa med händelsens bild.
Denna bild av klockan visar då händelsens koordinattid i mitt koordinatsystem.
__________________
2013-01-21
Som jag ser det visar MM:s försök ingenting annat än att Jorden (och mätanordningen) ligger stilla i
förhållande till den eter som den svävar i. Av detta kan man varken dra slutsatsen att
ljushastigheten alltid är konstant eller att ljusstrålar alltid är raka. Det finns mycket att säga om
detta och jag funderar på om jag kan åstadkomma en begriplig sammanfattning.
När jag läste om relativitetsteori gjorde man ett stort nummer av att man kan inte veta något om en
händelse förrän man nås av händelsens bild. Man hävdade att det innebär att man kan ersätta
händelsen med händelsens bild. Avståndet till händelsens bild kan man skriva som roten ur (x^2+y^
2+z^2-tc^2). Men argumentet håller inte. Bilden av en händelse är något annat än händelsen.
Om jag kör in i en blockerad vägkorsning växelverkar jag med händelsen "blockerad korsning".
Resultatet blir en händelse som kallas "krock". Om jag bromsar in när jag nås av bilden av
"blockerad korsning" växelverkar jag med bilden av "blockerad korsning". När korsningen blir fri kan
jag köra igenom rumskoordinaterna för "blockerad korsning" men eftersom tidskoordinaten då blir
en annan får jag ingen växelverkan med "blockerad korsning".
Som jag ser det kan man använda Minkowskimetrik för händelsers bilder. Det är inget fel i det. Det
kan i många fall vara ett användbart sätt att hantera problem. Men det ersätter inte behovet av att
hantera händelser.
__________________
2013-01-22
Som ett plankton svävar i en havsström svävar jag i en eter som blåser med ljushatighet i en
riktning som jag kallar koordinattidsriktningen. Föremål i min omgivning svävar i samma eter och ser
ut att stå stilla. Men etervindens riktning är inte alltid exakt densamma. Om den avviker vid ett
föremål ser jag det som att föremålet rör sig i förhållande till mig.
När jag kör med min bil vrider jag min koordinattidsaxel så att den bildar en vinkel med markens
koordinattidsruktning. Jag ändrar alltså etervindens riktning kring bilen. På samma sätt som luften i
kupen följer med bilen följer etern kring bilen med bilen. En MM-mätare i bilen kommer alltså att
visa att bilen ligger stilla i förhållande till etern i bilen liksom en MM-mätare på marken visar att
marken ligger stilla i förhållande till etern vid marken.
Jag kan inte komma från marken till bilen utan att accelerera. Mellan bilen och marken finns alltså
ett accelerationsskikt det vill säga ett gravitationsfält. Ljusstrålar kröks i ett gravitationsfält. När jag
tittar ut genom vindrutan på bilen ser jag alltså ljusstrålar som krökts i ett gravitationsfält.
När jag tittar ner i vattnet händer det att jag ser en fisk. Om jag med ett spjut hugger mot bilden av
fisken bommar jag. Ljusstrålarna kröks vid vattenytan så att bilden av fisken inte sammanfaller med
fisken. SR är ett sätt att hantera detta genom att flytta fisken till bilden så att man kan använda raka
ljusstrålar. En annan möjlighet är att räkna med krökta ljusstrålar som flyttar bilden till fisken.
När jag tittar ut genom vindrutan blir ljuskrökningen så liten att den inte spelar någon roll. Och för
hundra år sedan var det knappast något annat än en vetenskaplig spekulation. Men om jag till
exempel jobbar med tröghetsnavigering använder jag gravitationsfältspassagerna för att bestämma
hastighet så att jag med hjälp av hastighet och en klocka kan bestämma läge. Här spelar även
obetydliga gravitationsfält vid färdens början en stor roll.
Jag har aldrig funderat på om begreppet "händelsens bild" är vanligt. Bara på om det är begripligt
och det tror jag att det är.
__________________
2013-01-26
För att hantera min värld behöver jag en bild där jag kan lägga in ett koordinatsystem så att jag får
koordinater som jag kan räkna med. Om jag gör en bijektiv avbildning innehåller bilden all
information om världen. Det går då att från bilden återskapa världen och alla bildens egenskaper
kommer från världen. Om jag förenklar bilden genom att avbilda flera punkter på samma bildpunkt
blir min avbildning inte bijektiv. Min bild kommer då att innehålla dels egenskaper som kommer från
världen, dels egenskaper som kommer från avbildningsfel.
1872 lade Felix Klein fram det så kallade Erlangenprogrammet där avbildningar indelas i klasser
efter vad som är invariant vid transformationer. Minkowskiavbildning och reell avblidning har olika
invarianter och tillhör alltså olika klasser. Men om avbildningen är bijektiv ger den, oberoende av
klass, en fullständig bild som enbart innehåller verklighetens egenskaper. En beskrivning av ett
fenomen i den ena avbildningen har då sin motsvarighet i en beskrivning i den andra avbildningen.
Vår reella avbildning är ett självklart inslag i vårt medfödda och vårt inlärda beteende.
Relativitetsteorin medförde att man såg en del samband som man inte tidigare hade sett. Men det
innebär naturligtvis inte att man bara kan avbilda världen på ett enda sätt. En bijektiv avbildning
enligt Minkowski och en bijektiv reell avbildning måste beskriva fenomen på sätt som ger samma
försöksresultat. Världen bryr sig naturligtvis inte om vilken avbildningsklass jag valt att använda.
En tredimensionell reell avbildning är inte bijektiv. När jag projicerar en fyrdimensionell värld på en
tredimensionell bild får jag samma typ av projektionsfel som när jag projicerar en klotyta på ett plan
(jag tycker trots allt att liknelsen ger en uppfattning av problemet). Minkowskiavbildningen är
fyrdimensionell och om den är bijektiv måste det gå att göra en bijektiv reell avbildning. Allt som kan
beskrivas i den ena avbildningen har då sin motsvarighet i den andra.
Som jag ser det blir det då intressant att ställa frågan: "Hur gör jag en reell avbildning som visar
motsvarigheten till de samband som relativitetsteorin påvisade?".
Man kan naturligtvis invända att de samband som man påvisade inom relativitetsteorin nu är
välkända och inte behöver någon annan beskrivning men jag tror att en bra reell beskrivning kan
visa oss nya oväntade samband. Och det skulle ha fördelen att vi kan betrakta världen utan att
behöva fundera på vilken avbildningsklass vi skall välja. Och jag tror att det är intressant oberoende
av om man kallar det fysik eller vardagshantering eller något annat.
__________________
2013-01-27
Visst ger olika avbildningar olika bilder där samband ser olika ut. Det är ju det som är poängen med
att använda olika avbildningar. Och du har rätt i att det kan hända att några samband som blir enkla
i Minkowskis avbildning bli svårhanterliga i andra avbildningar. Har du något bra exempel på de
symmetrier du pratar om? Något som är baserat på odiskutabla mätningar.
I många tusen år har vi använt reell avbildning. Vi har sett samband som vi betraktar som så
självklara att vi inte längre ser dem. Det är inte så att vi bara projicerar på ett tredimensionellt rum
genom att sätta dt=0. Vi är mycket medvetna om tidskoordinaten även om vi inte alltid formulerar
detta. Vi stoppar mat i munnen utan att med formler beskriva hur det går till.
För drygt hundra år sedan provade vi att använda Minkowskis avbildning och upptäckte att den
visade några samband som vi inte sett tidigare. Det var ju intressant men det betydde naturligtvis
inte att vi funnit den enda rätta avbildningen. Fortfarande lever många människor hela sitt liv med
daglig användning av reell avbildning men utan att ägna en tanke åt Minkowskis avbildning.
Jag vet inte varför du återkommer till att ljushastigheten skall vara konstant. I den värld jag ser är
den inte det. Jag ser c som min hastighet i koordinattidsriktningen, alltså som omräkningsfaktor
mellan längdenheter och tidsenheter.
Och en liten detalj. Om jag projicerar ett klot på ett plan blir väl projektionen RÄTT i en punkt. Och
om jag avbildar ett tredimensionellt klot på ett tvådimensionell plan tar jag väl bort en dimension.
Det spelar ingen roll eftersom det bara handlar om en liknelse men jag undrade vad du menar.
__________________
2013-01-28
Längdkontraktionen och tidsdilationen är ju väldokumenterade fenomen så låt oss börja med det.
Då är vi tillbaka i Pelles lada. Förra gången tyckte du att jag uttryckte mig otydligt så jag tänker ta
det bitvis så får vi se om det blir begripligt.
Först en viktig skillnad mellan SO(3,1) och SO(4).
I SO(3,1) är en koordinataxel speciell. Tid är något annat än längd och man kan direkt på
koordinatsystemet se vilken axel som är tidsaxel. Men om det finns en ändlig hastighet för
informationsöverföring blir längd och tid beroende av varandra. Detta beroende lägger du i
invarianten. Genom att använda en icke-ortogonal transform får du en koppling mellan
tidskoordinater och längdkoordinater. Det är ju det som är tricket med lorentztransformen.
I SO(4) är alla koordinater av samma typ. Jag kan inte, bara genom att se på koordinatsystemet,
avgöra vilken axel som är tidsaxel. Jag måste skilja mellan rum och tid på något annat sätt. När jag
ser på en klocka ser jag att den visar allt högre värden. Om jag avsätter klockslag och årtal på en
koordinataxel får jag alltså värden som ständigt ökar. Jag färdas alltså längs denna koordinataxel. I
SO(4) kan jag vrida mitt koordinatsystem så att bara en av mina fyra koordinater ökar. Jag kan
alltså lägga en koordinataxel i min färdriktning. Jag kallar den koordinataxeln för koordinattidsaxel.
Pelle gör likadant men det är inte säkert att han färdas i samma riktning som jag och det är alltså
inte säkert att hans koordinattidsaxel blir parallell med min. Det som för mig är rum kan vara tid för
Pelle och tvärtom. Den koppling mellan tid och rum som du i SO(3,1) beskriver med hjälp av en icke-
ortogonal transform beskriver jag i SO(4) som en vridning av koordinattiden.
Under min livstid kommer jag bara att passera de punkter som ligger på min koordinattidsaxel. Om
jag inte går in i ladan ligger den i mitt rum och sträcker sig i koordinattid utefter min
koordinattidsaxel utan att min koordinattidsaxel går in i ladan. Jag kommer alltså inte att passera
genom ladan. För att Pelle skall kunna ta sig igenom ladan måste han vrida sin koordinattidsaxel så
att den går genom ladan. Pelle och jag får alltså icke-parallella tidsaxlar.
Är vi överens om att man kan göra så? Om att detta sätt att se på världen inte strider mot några
kända regler?
_________________
2013-01-29
Om det finns en högsta möjliga hastighet c kan jag använda denna för att omvandla mellan
tidsenheter och längdenheter. c har egentligen inte med ljushastighet att göra annat än att
ljushastigheten i en viss situation är den högsta hastighet vi funnit. Jag jobbade en gång i tiden med
hjälpmedel för blinda bland annat frågan om hur man skapar en avståndsuppfattning utan hjälp av
synen. Här kan man använda ljudhastigheten som c. Men det viktiga är att c är en ändlig konstant.
När jag graderar min koordinattidsaxel tar jag en klocka. När klockan (parametertiden) går en
tidsenhet avsätter jag en tidsenhet, det vill säga c längdenheter, på min koordinattidsaxel
(koordinattid). Jag färdas alltså en tidsenhet, det vill säga c längdenheter, i koordinattidsriktningen
när paramertiden går en tidsenhet.
Jag kan dividera rumshastigheten v med c. Eftersom c är största möjliga hastighet kommer v/c att
ligga mellan -1 och 1. En storhet som ligger mellan -1 och 1 kan jag skriva som sin(a). Detta är ett
ganska vanligt sätt att hantera sådana storheter. Om jag sätter v/c = sin(a) blir lorentzkontraktionen
cos(a).
Jag återkommer till användningen av (a) men först är frågan: "Kan jag göra så här?" Har jag gjort
något som strider mot kända regler?
__________________
2013-01-30
Om jag anger en punkts läge med fyra av varandra oberoende (ortogonala) koordinater blir
lägesangivelsen fullständig. Om jag kastar en sten mot ett byte och alla stenens fyra koordinater
överensstämmer med bytets motsvarande koordinater träffar jag alltid. Så länge någon av stenens
koordinater avviker från bytets motsvarande koordinat träffar jag aldrig. En avbildning på ett
fyrdimensionellt ortogonalt koordinatsystem är alltså bijektiv.
Såväl en avbildning på SO(3,1) som en avbildning på SO(4) är bijektiv. Båda ger alltså en fullständig
beskrivning av verkligheten som innebär att verkligheten kan återskapas från beskrivningen. Världen
bryr sig inte om om jag använder ett koordinatsystem med fyra likadana axlar eller ett
koordinatsystem där jag särbehandlar en axel. Men avbildningarna blir olika och jag kan inte
använda samband från SO(3,1) i SO(4). Däremot måste naturligtvis utfallet av försök bli samma
oavsett om jag använt en beskrivning i SO(3,1) eller SO(4).
Om ljushastigheten är densamma i alla riktningar blir ljusstrålar raka. För att en ljusstråle skall
krökas måste ljushastigheten vara lägre längs innerkurvan än längs ytterkurvan. MM:s försök visade
att ljushastigheten INOM ett referenssystem är lika i alla riktningar. Av det kan man inte dra några
slutsatser som handlar om övergångar mellan referenssystem.
Jag kan inte komma från ett referenssystem till ett annat utan acceleration. Mellan två
referenssystem finns alltså ett accelerationsfält alltså ett gravitationsfält. Stjärnan vid
solförmörkelsen visar att ljuset böjs i solens gravitationsfält. Eftersom den enda kunskap vi har om
vad som finns på avstånd kommer från ljus och liknande fenomen som når oss ser vi inte om
ljusstrålar är raka eller krokiga. I en prismakikare är en ljusstråle långt ifrån rak men när vi tittar i
kikaren märker vi ingenting av dessa krokar.
Med raka ljusstrålar kan man bara se rakt. En ljusstråle längs x-axeln visar enbart vad som händer
på x-axeln. Man kan inte set runt ett hörn. Men en krokig ljusstråle kan ha varit inne i en annan
dimension. Om ljusstrålar kan vara krokiga kan det längs x-axeln komma en stråle som visar vad
som hänt på t-axeln. x-koordinaterna blir då inte helt oberoende av t-koordinaterna.
Hur skall man hantera att ljusstrålar böjs vid övergången mellan två referenssystem?
En möjlighet är att med en icke-ortogonal transform vrida rummet så att tidsaxeln får en
rumsprojektion. Man kan då använda koordinatsystem som särbehandlar tidskoordinaten SO(3,1).
En annan är att vrida hela koordinatsystemet. Då ändras vad som är tid och vad som är rum vilket
kräver att alla axlar betraktas som likvärda och utbytbara SO(4).
Relativitetsteorin beskriver ett sätt att transformera mellan SO(3,1)-system på sådant sätt att
ljusstrålar beskrivs som raka. Det betyder naturligtvis inte att de ÄR raka. Begreppen rak och krokig
hör till vår beskrivning av världen. Det är först när vi beskriver en ljusstråle som vi kan tala om rak
eller krokig.
Världen kan beskrivas i SO(3,1) eller SO(4) (och på andra sätt). Men beskrivningen blir olika och
man kan inte utan vidare ta samband från en beskrivning i SO(3,1) och använda dem i SO(4). Varje
beskrivning måste bygga på sina egna regler och övergång mellan beskrivningarna måste göras
med hjälp av regelövergångar.
__________________
2013-01-31
Då var det dags för längdkontraktion och tidsdilation i SO(4).
När Pelle springer genom ladan skall han se en kortare lada och jag skall se en Pelle som färdas
långsammare än jag i min koordinattidsriktning. Blir det så?
Sätt v/c till sin(a) och tolka (a) som vinkeln mellan min och Pelles koordinattidsaxlar. Då blir
lorentzkontraktionen cos(a). Och vinkeln mellan min och Pelles x-axel blir också (a). I Pelles system
får ladan en komposant i x-led och en komposant i t-led. x-komposanten blir ladans längd gånger
cos(a) (längdkontraktion) och t-komposanten blir ladans längd gånger sin(a).
När jag färdas T enheter längs min koordinattidsaxel färdas Pelle T enheter längs sin
koordinattidsaxel. Men eftersom Pelle delvis färdas i mitt rum, alltså i min x-riktning, kommer han att
färdas långsammare i min koordinattidsriktning. Han färdas bara Tcos(a) i min koordinattidsriktning
(tidsdilation) och i min x-riktning färdas han Tsin(a).
__________________
2013-02-01
Jag är naturligtvis medveten om att du kan ha rätt. Men om jag skall felförklara den avbildning som
människor använt i tusentals år och funnit användbar och pålitlig vill jag ha mycket påtagliga bevis.
Att man kan använda en annan avbildning är inte något bevis på att den gamla är fel Men - visst.
Jag tänker ibland på vilka konsekvenser det skulle ha men först vill jag veta hur jag kan använda den
gamla vanliga avbildningen.
Det är uppenbart att vi använder begreppet tid på sätt som vi inte kan använda rumskoordinater.
Som jag ser det beror det på att vi använder tid som ett sammanfattningsbegrepp för två olika
begrepp, parametertid och koordinattid. Parametertid är en skalär förändringsparameter,
koordinattiden är en koordinat av samma typ som rumskoordinaterna.
Om c är högsta möjliga hatighet och jag färdas med hastigheten c i koordinattidsled kan jag ju inte
röra mig fritt i koordinattidsled. Men det finns mycket att säga om detta. Jag skall försöka
återkomma.
Så vitt jag kunnat finna handlar alla MM-mätningar om mätningar inom ett referenssystem. Inga
delar av mätanordningarna rör sig i förhållande till varandra med hastigheter som närmar sig
ljushastighet. Då säger inte mätningarna något om övergångar mellan referenssystem.
Maxwells ekvationer säger inte alls att ljushastigheten är densamma i alla referenssystem. De säger
att ljushastigheten är ett genom roten ur produkten av det ljusbärande mediets
dielektricitetskonstant och magnetiska permeabilitet. Det är till exempel väl känt att ljushastigheten i
glas är lägre än i luft. Det är grunden för hela optiken. Och det handlar inte om att ljuset "studsar"
sig genom glaset. Vi kan mäta dielektricitetskonstant och magnetisk permeabilitet med metoder som
inte använder ljus och se att resultatet stämmer.
__________________
2013-02-01
Om avståndet mellan två punkter i euklidisk metrik är noll sammanfaller punkterna. Det är i så fall
en dubbelräkning av samma punkt. Det är ju detta som är innebörden i att avbildningen är bijektiv.
Man lägger aldrig två olika punkter med avståndet noll. Men detta gäller bara om man anger läget
med fyra koordinater. Det visste redan neandertalaren som kastade sten mot ett byte. Men vi
använder också tid som en förändringsparameter. Som jag ser det är det uppenbart att detta är två
olika sätt att använda tidsbegreppet. För mig är detta så självklart att jag har svårt att uttrycka det
tydligare.
Jag färdas med hastigheten c i min koordinattidsriktning. Jag kan varken röra mig fortare eller
långsammare. Men det intressanta är att Pelle kan färdas i en annan riktning. Och under vissa
förutsättningar kan han tala om vad han ser.
__________________
2013-20-02
Om världen är fyrdimensionell kan den avbildas bijektivt på en fyrdimensionell bild. Det betyder att
man till varje bildpunkt knyter en och endast en verklighetspunkt.
Både R^4 och R^(1,3) är fyrdimensionella och det går alltså att lägga en bijektiv bild på dem.
I stället för att lägga bijektiva bilder kan jag lägga en euklidisk bild på R^4 och en minkowskibild på
R^(1,3). Med euklidisk bild menar jag en bild där jag på varje bildpunkt lägger alla
verklighetspunkter med det euklidiska avståndet noll mellan sig. Och med minkowskibild menar jag
en bild där jag lägger alla verklighetspunkter med minkowskiavståndet noll mellan sig på samma
bildpunkt.
Om jag tar en verklighetspunkt så finns det inga andra verklighetspunkter på det euklidiska
avståndet noll. Den euklidiska bilden blir alltså bijektiv. Däremot finns det en grupp
verklighetspunkter som har minkowskiavståndet noll mellan sig. Minkowskibilden blir alltså inte
bijektiv. Jag kan inte återskapa verkligheten från minkowskibilden.
En regel som i den euklidiska bilden pekar ut en bildpunkt pekar entydigt ut en verklighetspunkt. En
regel som i minkowskibilden pekar ut en bildpunkt pekar ut en grupp verklighetspunkter. Detta är en
fundamental skillnad mellan regler i den euklidiska bilden och regler i minkowskibilden. Man kan
med matematiska metoder visa att bildernas regler är fundamentalt olika men det viktiga är att man
vet vari olikheten består.
När man i praktiken försöker använda minkowskibilden upptäcker man snart att den inte räcker. Man
behöver bara försöka följa fasläget i ett växelströmsnät eller räkna på fading mellan signaler med
olika gångväg eller bestämma position med hjälp av satelitklockor för att upptäcka att man måste
komplettera minkowskiavståndet med det euklidiska avståndet.
Jag kan naturligtvis komplettera minkowskibilden med den euklidiska bilden så att jag får en bijektiv
bild men då använder jag ju den euklidiska bilden.
Effekter på ljusstrålar och effekter av en påstådd eter är väl helt enkelt samma sak. Och jag ser
inget konstigt i att ett medium påverkas av acceleration.
Kausalitet är en stor fråga. Det behövs mer än några rader om det.
__________________
2013-02-03
Om jag gör en bijektiv avbildning (A) av verkligheten använder jag en regel som knyter varje
verklighetspunkt till en och endast en bildpunkt. Omvändningen av denna regel lägger tillbaka
bildpunkten på verklighetspunkten och återskapar alltså förlagan från bilden. Om jag så gör en
annan bijektiv bild (B) med en annan regel får jag två olika bilder. Om jag då tillämpar B:s regel på
omvändningen av A:s regel får jag en regel som avbildar A på B. Om två bilder är bijektiva
avbildningar av samma förlaga finns det alltså en regel som avbildar den ena på den andra.
Om världen är symmetrisk kan man dela in den i undergrupper där varje undergrupp har någon
gemensam egenskap. Om man inte är intresserad av förhållandena inom varje undergrupp kan man
använda en icke-bijektiv avbildning där varje bildpunkt inte svarar mot en verklighetspunkt utan mot
en sådan undergrupp.
Om världen har andra icke-materiella egenskaper kommer de inte med i någon form av avbildning.
De ligger alltså helt utanför den här diskussionen.
Jag färdas mot min framtid. Om jag inte gör något är min framtid Vendelsös framtid. Men om jag
tar bilen och kör mot Karlstad där min far bodde ändras min färdriktning så att min framtid blir
Karlstads framtid. Min färdriktning bildar alltså en vinkel med markens färdriktning. När jag ser på
min hastighetsmätare visar den sinus för denna vinkel. Jag brukar se det som att hastighetsmätaren
visar nanosinus som ju är ungefär samma som km/h. När hastighetsmätaren visar 90 färdas jag
alltså med 90 nanosinus mot Karlstads framtid. När jag kommer fram till Karlstads börjar jag lägga
Karlstads dåtid till min dåtid.
När min far levde ringde han ibland och berättade vad som hänt i Karlstad. Utan att min
koordinattidsaxel gått genom Karlstad kunde jag då lägga in en del av Karlstads dåtid i min dåtid.
Jag tror att de flesta människor ser detta som så självklart att det inte behöver formuleras. Men jag
tror att det är viktigt att göra det så att jag kan se mer i detalj på vad det innebär.
__________________
2013-02-03
Ja. Det är ju som du säger inledningsvis så att man kan se världen på olika sätt (olika metriker). En
fördel med att vrida koordinatsystemet med arcsin(v/c) är att när du kommer till 90 grader byter
tidsaxeln plats med en rumsaxel och om du fortsätter vridningen kommer tiden att gå bakåt sett från
en utomstående betraktare. För den som faller in i hålet blir däremot allt oförändrat. Frågan om hur
man beskriver ett fall in i ett svart hål var en anledning till att jag tyckte den beskrivningen var
intressant.
__________________
2013-02-04
PuffTheDragon har på https://www.flashback.org/sp37376762 en beskrivning av situationen vid ett
svart hål.
Om vi hittar ett svart hål inom räckhåll kommer vi att kunna skicka ett rymdskepp genom det. Vad
händer när skeppet passerar genom hålet?
Antag att det finns två instrument på skeppets instrumentbräda. Det ena är en radiostyrd klocka som
visar tid enligt ett atomur på Jorden och det andra är en avståndsmätare som visar avståndet från
Jorden. Före start är det lätt att se vilket som är avståndsmätare och vilket som är klocka. Klockan
går och avståndsmätaren står stilla. När skeppet tar fart börjar avståndsmätaren att gå och klockan
saktar in.
Skeppet får falla i fritt fall mot hålet. När det når händelsehorisonten har det kommit upp i
ljushastighet. Klockan har stannat men avståndsmätaren går på samma sätt som klockan gjorde
före start. Klocka och avståndsmätare ser alltså ut att ha bytt plats. En av mina rumsaxlar har blivit
skeppets koordinattidsaxel och min koordinattidsaxel har blivit en av skeppets rumsaxlar. Men
frånsett att instrumenten bytt plats märker besättningen ingenting av händelsehorisontpassagen.
Ombord på skeppet fungerar alla naturlagar som vanligt. Skeppets koordinatsystem har vridits i
förhållande till mitt koordinatsystem men det har inte genomgått några inre förändringar. En vanlig
klocka ombord på skeppet går som avståndsmätaren.
När skeppet kommit innanför händelsehorisonten börjar klockan på instrumentbrädan att gå
baklänges och avståndsmätaren saktar in. Skeppet kan nu inte längre kommunicera med Jorden
men för besättningen är allt annat som vanligt. Man fortsätter att skriva i loggboken. Man daterar
loggboken både efter instrumentbrädesklockan, avståndsmätaren och den vanliga klockan.
När skeppet passerat hålets centrum har det rörelseenergi nog att fortsätta ut ur hålet. När det på
nytt passerar händelsehorisonten kan det åter börja rapportera till Jorden. Vi kan då få veta något
om hur det ser ut inne i hålet.
__________________
2013-02-04
Världen i sig har inga koordinater. För att få koordinater som jag kan använda måste jag avbilda
världen på ett koordinatsystem. Vilken typ av koordinater jag då får beror på vilken typ av
koordinatsystem jag valt och vilken typ av avbildning jag använt.
Som jag ser det har jag fyra koordinataxlar varav en pekar mot min framtid. Om vi har en väg som
går mellan gården och handelsboden kan jag och min kompis gå mot handelsboden medan du går
mot gården. Min koordinattidsaxel pekar då mot handelsbodens framtid och din pekar mot gårdens
framtid. Mitt på vägen möts vi och konstaterar att våra framtider ligger mycket nära varandra men
att det finns en liten skillnad som gör att vi kommer att ha ett rumsavstånd när vi kommer fram.
Jag och allt i min närmaste omgivning färdas mot nästan samma framtid. Det innebär att det
vanligtvis är självklart vad som skall vara koordinattidsriktning. Men vad som är koordinattidsriktning
är inte en egenskap hos världen. För ett rymdskepp som passerar mig med en hastighet som ligger
nära ljushastighet kan det som för mig är rum vara koordinattid.
__________________
2013-02-06
Du har helt rätt i att R^4 , R^(3,1) och R^(2,2) alla är fyrdimensionella och alltså kan ta emot en
bijektiv bild av verkligheten. Om information kunde överföras med oändlig hastighet skulle det inte
spela någon roll om man separerade axlarna eller inte. Då kunde man hantera varje koordinat som
oberoende av de övriga. Men om det finns en maximal hastighet blir inte tid och rum alltid
oberoende av varandra. Om jag sänder en signal för att påverka en stjärna som ligger på
rumsavståndet en miljon ljusår tar det två miljoner år innan jag får veta resultatet. Stjärnan är
alltså avlägsen både i tid och rum. Och när man transformerar mellan system som rör sig i
förhållande till varandra får rumskoordinater tidsprojektioner och tvärtom. Frågan är då hur man
hanterar detta.
Om man har separerat en axel som tidsaxel kan man inte direkt vrida in den i rummet för att kunna
projicera rums- och tidskoordinater på varandra. Man behöver använda en icke-ortogonal transform
för att projicera rum och tid på varandra. Den fråga jag en gång i tiden ställde mig var: "Kan jag
inte i stället vrida det ortogonala systemet i R^4?" Det kan jag naturligtvis göra. Världen bryr sig inte
om hur jag avbildar den eller hur jag hanterar dess bild. Frågan är om jag kan tolka en sådan bild
på ett vettigt sätt. Jag har nu använt det här synsättet i några årtionden och inte funnit något som
talar mot det. Men det betyder naturligtvis inte att det är det enda rätta, bara att det ibland är
användbart.
När det gäller kausaliteten så menar jag att vi ibland använder tid som en förändringsparameter
alltså som ett sätt att ordna händelser i löpande följd. Som jag ser det har detta inte direkt med
läge att göra. Det är därför jag ser parametertiden som något annat än koordinattiden. Kausalitet
avgörs alltså av parametertid. Om det finns ett orsaksamband mellan två händelser är den med
lägst parametertid orsak.
När parametertiden går färdas jag längs min koordinattidsaxel. De punkter jag lämnar kallar jag
dåtid, den punkt där jag befinner mig kallar jag nu och de punkter som ligger framför mig kallar jag
framtid. Pelle som far förbi i ett rymdskepp gör likadant med sin koordinattidsaxel. Att det råkar vara
en av mina rumsaxlar är inget som han märker något av.
Om jag vill påverka en händelse på rumsavstånd måste jag skicka en påverkanssignal. Den punkt på
min koordinattidsaxel där jag gör det kallar jag händelsens påverkansnu. Den punkt på min
koordinattidsaxel där jag befinner mig vid den parametertid som händelsen inträffar vid kallar jag
händelsens samtidsnu. Den punkt på min koordinattidsaxel där jag befinner mig där
bekräftelsebilden av händelsen når mig kallar jag händelsens observationsnu. Vid händelsens
påverkansnu och observationsnu är minkowskiavståndet till händelsen noll.
Jag sätter v/c = sin(a) där (a) är min vridningsvinkel. Eftersom sin inte kan bli större än ett behöver
jag då ingen begränsning av vridningsvinkeln. Även vridning mer än 90 grader kan ges en tolkning
vilket kommer att bli aktuellt när vi någon gång i framtiden börjar färdas genom svarta hål.
Lika lite som koordinatsystemet finns i verkligheten finns vridningsvinkeln i verkligheten. Den är en
egenskap hos det koordinatsystem jag valt. Men skall man leta efter en känguru är det kanske där
man skall leta. Men det är inte lätt att hitta genomförbara experiment som kan visa vad som gäller.
För de hastigheter vi normalt hanterar är skillnaden mellan sin och tan inte mätbara.
__________________
2013-02-07
Jag vet inte hur man hanterar bilder men vi kanske återigen kan använda dbshw:s bild
Vi försöker igen.
Jag använder din figur. Som jag ser det är den blå linjen Pelles t-axel. Längden i den blå riktningen
är alltså vad Pelles stoppur visar för Pelle. Han springer nu så att den blå sträckan som du angett
som "längre än 50 m/0,99c" blir 50/0,99c. Den röda sträckan som du angett som "50 m/0,99c" är
min tolkning av Kalles signal vilken alltså är mindre än 50/0,99c. Genom att Pelle delvis springer i
mitt rum rör han sig långsammare i min koordinattidsriktning (t-riktning).
Minkowskimetriken bygger på tanken att det finns ett tidsavstånd som kan uppväga ett rumsavstånd
så att resultatet blir noll. Om tidsavståndet är lika med rumsavståndet blir Minkowskiavståndet noll.
Detta fungerar i många fall eftersom vi upplever bilden av en händelse som om den var händelsen.
Vi är tydligen överens om att två punkter med Minkowskiavståndet noll kan ha ett reellt avstånd.
Som jag ser det betyder det att man även måste hålla reda på det reella avståndet vilket
Minkowskimetriken inte gör. Som jag ser det kan Minkowskimetriken komplettera den reella
metriken men inte ersätta den.
__________________
2013-01-14
Om jag ser en stjärna explodera säger jag: "Nu exploderade stjärnan."
Så tänker jag efter och ändrar det till: "Nu blev minkowskiavståndet till stjärnexplosionen noll. Hur
skall jag lägga in det i mitt koordinatsystem?"
Om stjärnan ligger en miljon ljusår bort och om det hade funnits en enorm klocka på stjärnan som
jag kunde se skulle jag se att klockan visade en tidpunkt för en miljon år sedan. Jag ritar då ett
koordinatsystem med en t-axel och en x-axel och med mig i origo. Så lägger jag in
stjärnexplosionen vid t lika med minus en miljon år och x lika med en miljon ljusår.
Stjärnexplosionens koordinattid i mitt system blir alltså minus en miljon år. Sedan dess har
parametertiden gått och jag ha färdats längs min t-axel så att jag nu kommit till origo. Och bilden av
stjärnexplosionen har färdats längs min x-axel så att den nu nått origo där jag kan se den. Från
origo är avståndet i t-riktningen lika stort som avståndet i x-riktningen vilket innebär att
minkowskiavståndet är noll.
Jag tror att detta är ett mycket vanligt sätt att se situationen.
__________________
2013-01-15
Det är mycket möjligt att man inte behöver något annat avståndsbegrepp i relativitetsteori. Men
relativitetsteori är inte hela världen. Den har funnits i cirka hundra år men den reella metriken har vi
använt i många tusen år. Jag tar inte ett steg utan en mängd avståndsbedömningar till väggar. golv.
möbler med mera.
Du har sagt någon gång att man kan bortse från relativitetsteori i vardagen. Att man alltså kan se
relativitetsteori som en spekulation fristående från vardagens verklighet. Så var det kanske för
hundra år sedan men det har hänt en del sedan dess. Vi möter idag en hel del fenomen där
ljushastigheten spelar en viktig roll.
Hela radartekniken bygger på att rumsavståndet är lika med tidsavståndet när minkowskiavståndet
är noll. I GPS använder vi skillnader i koordinattid mellan reellt synkrona klockor placerade i sateliter
med kända lägen. Vi bygger allt större växelströmsnät med mimkowskisynkronism. När jag bygger
ett kretskort för att hantera datorpulser måste jag tänka på att en nanosekundpuls inte är längre än
en fot. När jag ringer till Australien får jag ibland en fördröjning som kräver en viss samtalsdisiplin.
Vi är på väg mot rymdfärder över avstånd där skillnaden mellan parametertid och koordinattid
spelar stor roll.
Allt oftare dyker de samband som ursprungligen härleddes via relativitetsteori upp i andra
sammanhang och med annan härledning. Som jag ser det är det viktigt att ha någon uppfattning om
hur olika synsätt hänger samman.
Minkowskimetriken är inte en egenskap hos verkligheten. Den är en transform som skapats via en
transformationsregel. När jag fotograferade med negativ färgfilm fick jag en en bild där färgerna
transformerats via en transformationsregel. Men eftersom denna regel var bijektiv kunde man vända
på regeln och kopiera bilderna tillbaka till förlagans färger. På samma sätt transformerar man till
minkowskimetriken via en transformationsregel. Men genom att man låser ett samband mellan
tidsavstånd och rumsavstånd blir denna transform inte bijektiv. Det går alltså inte att från
minkowskimetrikens bild bestämma reella avstånd. Minkowskimetriken kan därför bara komplettera
den reella metriken, inte ersätta den.
Det är inte något fel i att använda transformer. Laplace-transformer är mycket användbara inom
reglerteknik, Fourier-transformer är utmärkta när man bygger förstärkare och minkowskimetriken
har ett klart tillämpningsområde. Men en transform är aldrig det enda möjliga synsättet.
Det finns en egendomlig inställning att alla måste se allt på samma sätt. Så är det inte. Det är
genom att vi ser saker på olika sätt som vi kan hitta nya möjligheter. Men då behöver vi tala om för
varandra vad vi ser och naturligtvis måste vi vara öppna för att anpassa vårt synsätt så att det
stämmer med de fenomen som vi observerar.
__________________
2013-01-17
Det reella avståndet till en händelse är roten ur (x^2+y^2+z^2+tc^2).
En händelse kan orsaka en bild som med hastigheten c utbreder sig i alla riktningar. Avståndet till
händelsens bild ärroten ur ( x^2+y^2+z^2-tc^2). Minkowskiavståndet till en händelse är alltså
avståndet till händelsens bild. Eftersom mottagandet av händelsens bild är mitt enda sätt att få veta
något om händelsen kan jag i många fall ersätta händelsen med händelsens bild.
Världen påverkas inte av mitt sätt att avbilda den. Jag kan välja om jag vill avbilda på ett
koordinatsystem med raka eller krokiga, reella eller imaginära axlar. En bild av världen avbildar även
alla fenomen som vi observerat. Det kan vara lämpligt att välja en avbildning som ger en lättanvänd
beskrivning av världen inklusive dess fenomen. Även om jag inte lyckats beskriva det tillräckligt
tydligt har jag försökt tala om att jag använder ett fyrdimensionellt koordinatsystem med raka
ortogonala reella axlar. Om jag i detta beskriver rumshastighet som en vridning av
koordinattidsaxeln så att rumshastigheten blir lika med c gånger sinus för vridningsvinkeln får jag
enkla uttryck för längdkontraktionen och tidsdilationen.
Varje gång en detekterbar händelse inträffar någon stans i universum förändras det och
parametertiden inkrementeras. Parametertid är alltså antalet minsta detekterbara händelser i
universum. Ett antal är en skalär storhet. Varje förändring av universum innebär att mitt läge i
förhållande till mitt omgivande universum förändras. Det lägger jag in i mitt koordinatsystem som att
jag flyttar mig en tidsenhet lika med c längdenheter längs min koordinattidsaxel när parametertiden
ökar med en tidsenhet.
En klocka räknar antalet händelser i ett tidsgivande element. Eftersom det tidsgivande elementet är
en viss andel av hela universum blir detta ett mått på antalet händelser i hela universum. En klocka
mäter alltså parametertid.
Om det vid en händelse finns en klocka kommer bilden av klockan att följa med händelsens bild.
Denna bild av klockan visar då händelsens koordinattid i mitt koordinatsystem.
__________________
2013-01-21
Som jag ser det visar MM:s försök ingenting annat än att Jorden (och mätanordningen) ligger stilla i
förhållande till den eter som den svävar i. Av detta kan man varken dra slutsatsen att
ljushastigheten alltid är konstant eller att ljusstrålar alltid är raka. Det finns mycket att säga om
detta och jag funderar på om jag kan åstadkomma en begriplig sammanfattning.
När jag läste om relativitetsteori gjorde man ett stort nummer av att man kan inte veta något om en
händelse förrän man nås av händelsens bild. Man hävdade att det innebär att man kan ersätta
händelsen med händelsens bild. Avståndet till händelsens bild kan man skriva som roten ur (x^2+y^
2+z^2-tc^2). Men argumentet håller inte. Bilden av en händelse är något annat än händelsen.
Om jag kör in i en blockerad vägkorsning växelverkar jag med händelsen "blockerad korsning".
Resultatet blir en händelse som kallas "krock". Om jag bromsar in när jag nås av bilden av
"blockerad korsning" växelverkar jag med bilden av "blockerad korsning". När korsningen blir fri kan
jag köra igenom rumskoordinaterna för "blockerad korsning" men eftersom tidskoordinaten då blir
en annan får jag ingen växelverkan med "blockerad korsning".
Som jag ser det kan man använda Minkowskimetrik för händelsers bilder. Det är inget fel i det. Det
kan i många fall vara ett användbart sätt att hantera problem. Men det ersätter inte behovet av att
hantera händelser.
__________________
2013-01-22
Som ett plankton svävar i en havsström svävar jag i en eter som blåser med ljushatighet i en
riktning som jag kallar koordinattidsriktningen. Föremål i min omgivning svävar i samma eter och ser
ut att stå stilla. Men etervindens riktning är inte alltid exakt densamma. Om den avviker vid ett
föremål ser jag det som att föremålet rör sig i förhållande till mig.
När jag kör med min bil vrider jag min koordinattidsaxel så att den bildar en vinkel med markens
koordinattidsruktning. Jag ändrar alltså etervindens riktning kring bilen. På samma sätt som luften i
kupen följer med bilen följer etern kring bilen med bilen. En MM-mätare i bilen kommer alltså att
visa att bilen ligger stilla i förhållande till etern i bilen liksom en MM-mätare på marken visar att
marken ligger stilla i förhållande till etern vid marken.
Jag kan inte komma från marken till bilen utan att accelerera. Mellan bilen och marken finns alltså
ett accelerationsskikt det vill säga ett gravitationsfält. Ljusstrålar kröks i ett gravitationsfält. När jag
tittar ut genom vindrutan på bilen ser jag alltså ljusstrålar som krökts i ett gravitationsfält.
När jag tittar ner i vattnet händer det att jag ser en fisk. Om jag med ett spjut hugger mot bilden av
fisken bommar jag. Ljusstrålarna kröks vid vattenytan så att bilden av fisken inte sammanfaller med
fisken. SR är ett sätt att hantera detta genom att flytta fisken till bilden så att man kan använda raka
ljusstrålar. En annan möjlighet är att räkna med krökta ljusstrålar som flyttar bilden till fisken.
När jag tittar ut genom vindrutan blir ljuskrökningen så liten att den inte spelar någon roll. Och för
hundra år sedan var det knappast något annat än en vetenskaplig spekulation. Men om jag till
exempel jobbar med tröghetsnavigering använder jag gravitationsfältspassagerna för att bestämma
hastighet så att jag med hjälp av hastighet och en klocka kan bestämma läge. Här spelar även
obetydliga gravitationsfält vid färdens början en stor roll.
Jag har aldrig funderat på om begreppet "händelsens bild" är vanligt. Bara på om det är begripligt
och det tror jag att det är.
__________________
2013-01-26
För att hantera min värld behöver jag en bild där jag kan lägga in ett koordinatsystem så att jag får
koordinater som jag kan räkna med. Om jag gör en bijektiv avbildning innehåller bilden all
information om världen. Det går då att från bilden återskapa världen och alla bildens egenskaper
kommer från världen. Om jag förenklar bilden genom att avbilda flera punkter på samma bildpunkt
blir min avbildning inte bijektiv. Min bild kommer då att innehålla dels egenskaper som kommer från
världen, dels egenskaper som kommer från avbildningsfel.
1872 lade Felix Klein fram det så kallade Erlangenprogrammet där avbildningar indelas i klasser
efter vad som är invariant vid transformationer. Minkowskiavbildning och reell avblidning har olika
invarianter och tillhör alltså olika klasser. Men om avbildningen är bijektiv ger den, oberoende av
klass, en fullständig bild som enbart innehåller verklighetens egenskaper. En beskrivning av ett
fenomen i den ena avbildningen har då sin motsvarighet i en beskrivning i den andra avbildningen.
Vår reella avbildning är ett självklart inslag i vårt medfödda och vårt inlärda beteende.
Relativitetsteorin medförde att man såg en del samband som man inte tidigare hade sett. Men det
innebär naturligtvis inte att man bara kan avbilda världen på ett enda sätt. En bijektiv avbildning
enligt Minkowski och en bijektiv reell avbildning måste beskriva fenomen på sätt som ger samma
försöksresultat. Världen bryr sig naturligtvis inte om vilken avbildningsklass jag valt att använda.
En tredimensionell reell avbildning är inte bijektiv. När jag projicerar en fyrdimensionell värld på en
tredimensionell bild får jag samma typ av projektionsfel som när jag projicerar en klotyta på ett plan
(jag tycker trots allt att liknelsen ger en uppfattning av problemet). Minkowskiavbildningen är
fyrdimensionell och om den är bijektiv måste det gå att göra en bijektiv reell avbildning. Allt som kan
beskrivas i den ena avbildningen har då sin motsvarighet i den andra.
Som jag ser det blir det då intressant att ställa frågan: "Hur gör jag en reell avbildning som visar
motsvarigheten till de samband som relativitetsteorin påvisade?".
Man kan naturligtvis invända att de samband som man påvisade inom relativitetsteorin nu är
välkända och inte behöver någon annan beskrivning men jag tror att en bra reell beskrivning kan
visa oss nya oväntade samband. Och det skulle ha fördelen att vi kan betrakta världen utan att
behöva fundera på vilken avbildningsklass vi skall välja. Och jag tror att det är intressant oberoende
av om man kallar det fysik eller vardagshantering eller något annat.
__________________
2013-01-27
Visst ger olika avbildningar olika bilder där samband ser olika ut. Det är ju det som är poängen med
att använda olika avbildningar. Och du har rätt i att det kan hända att några samband som blir enkla
i Minkowskis avbildning bli svårhanterliga i andra avbildningar. Har du något bra exempel på de
symmetrier du pratar om? Något som är baserat på odiskutabla mätningar.
I många tusen år har vi använt reell avbildning. Vi har sett samband som vi betraktar som så
självklara att vi inte längre ser dem. Det är inte så att vi bara projicerar på ett tredimensionellt rum
genom att sätta dt=0. Vi är mycket medvetna om tidskoordinaten även om vi inte alltid formulerar
detta. Vi stoppar mat i munnen utan att med formler beskriva hur det går till.
För drygt hundra år sedan provade vi att använda Minkowskis avbildning och upptäckte att den
visade några samband som vi inte sett tidigare. Det var ju intressant men det betydde naturligtvis
inte att vi funnit den enda rätta avbildningen. Fortfarande lever många människor hela sitt liv med
daglig användning av reell avbildning men utan att ägna en tanke åt Minkowskis avbildning.
Jag vet inte varför du återkommer till att ljushastigheten skall vara konstant. I den värld jag ser är
den inte det. Jag ser c som min hastighet i koordinattidsriktningen, alltså som omräkningsfaktor
mellan längdenheter och tidsenheter.
Och en liten detalj. Om jag projicerar ett klot på ett plan blir väl projektionen RÄTT i en punkt. Och
om jag avbildar ett tredimensionellt klot på ett tvådimensionell plan tar jag väl bort en dimension.
Det spelar ingen roll eftersom det bara handlar om en liknelse men jag undrade vad du menar.
__________________
2013-01-28
Längdkontraktionen och tidsdilationen är ju väldokumenterade fenomen så låt oss börja med det.
Då är vi tillbaka i Pelles lada. Förra gången tyckte du att jag uttryckte mig otydligt så jag tänker ta
det bitvis så får vi se om det blir begripligt.
Först en viktig skillnad mellan SO(3,1) och SO(4).
I SO(3,1) är en koordinataxel speciell. Tid är något annat än längd och man kan direkt på
koordinatsystemet se vilken axel som är tidsaxel. Men om det finns en ändlig hastighet för
informationsöverföring blir längd och tid beroende av varandra. Detta beroende lägger du i
invarianten. Genom att använda en icke-ortogonal transform får du en koppling mellan
tidskoordinater och längdkoordinater. Det är ju det som är tricket med lorentztransformen.
I SO(4) är alla koordinater av samma typ. Jag kan inte, bara genom att se på koordinatsystemet,
avgöra vilken axel som är tidsaxel. Jag måste skilja mellan rum och tid på något annat sätt. När jag
ser på en klocka ser jag att den visar allt högre värden. Om jag avsätter klockslag och årtal på en
koordinataxel får jag alltså värden som ständigt ökar. Jag färdas alltså längs denna koordinataxel. I
SO(4) kan jag vrida mitt koordinatsystem så att bara en av mina fyra koordinater ökar. Jag kan
alltså lägga en koordinataxel i min färdriktning. Jag kallar den koordinataxeln för koordinattidsaxel.
Pelle gör likadant men det är inte säkert att han färdas i samma riktning som jag och det är alltså
inte säkert att hans koordinattidsaxel blir parallell med min. Det som för mig är rum kan vara tid för
Pelle och tvärtom. Den koppling mellan tid och rum som du i SO(3,1) beskriver med hjälp av en icke-
ortogonal transform beskriver jag i SO(4) som en vridning av koordinattiden.
Under min livstid kommer jag bara att passera de punkter som ligger på min koordinattidsaxel. Om
jag inte går in i ladan ligger den i mitt rum och sträcker sig i koordinattid utefter min
koordinattidsaxel utan att min koordinattidsaxel går in i ladan. Jag kommer alltså inte att passera
genom ladan. För att Pelle skall kunna ta sig igenom ladan måste han vrida sin koordinattidsaxel så
att den går genom ladan. Pelle och jag får alltså icke-parallella tidsaxlar.
Är vi överens om att man kan göra så? Om att detta sätt att se på världen inte strider mot några
kända regler?
_________________
2013-01-29
Om det finns en högsta möjliga hastighet c kan jag använda denna för att omvandla mellan
tidsenheter och längdenheter. c har egentligen inte med ljushastighet att göra annat än att
ljushastigheten i en viss situation är den högsta hastighet vi funnit. Jag jobbade en gång i tiden med
hjälpmedel för blinda bland annat frågan om hur man skapar en avståndsuppfattning utan hjälp av
synen. Här kan man använda ljudhastigheten som c. Men det viktiga är att c är en ändlig konstant.
När jag graderar min koordinattidsaxel tar jag en klocka. När klockan (parametertiden) går en
tidsenhet avsätter jag en tidsenhet, det vill säga c längdenheter, på min koordinattidsaxel
(koordinattid). Jag färdas alltså en tidsenhet, det vill säga c längdenheter, i koordinattidsriktningen
när paramertiden går en tidsenhet.
Jag kan dividera rumshastigheten v med c. Eftersom c är största möjliga hastighet kommer v/c att
ligga mellan -1 och 1. En storhet som ligger mellan -1 och 1 kan jag skriva som sin(a). Detta är ett
ganska vanligt sätt att hantera sådana storheter. Om jag sätter v/c = sin(a) blir lorentzkontraktionen
cos(a).
Jag återkommer till användningen av (a) men först är frågan: "Kan jag göra så här?" Har jag gjort
något som strider mot kända regler?
__________________
2013-01-30
Om jag anger en punkts läge med fyra av varandra oberoende (ortogonala) koordinater blir
lägesangivelsen fullständig. Om jag kastar en sten mot ett byte och alla stenens fyra koordinater
överensstämmer med bytets motsvarande koordinater träffar jag alltid. Så länge någon av stenens
koordinater avviker från bytets motsvarande koordinat träffar jag aldrig. En avbildning på ett
fyrdimensionellt ortogonalt koordinatsystem är alltså bijektiv.
Såväl en avbildning på SO(3,1) som en avbildning på SO(4) är bijektiv. Båda ger alltså en fullständig
beskrivning av verkligheten som innebär att verkligheten kan återskapas från beskrivningen. Världen
bryr sig inte om om jag använder ett koordinatsystem med fyra likadana axlar eller ett
koordinatsystem där jag särbehandlar en axel. Men avbildningarna blir olika och jag kan inte
använda samband från SO(3,1) i SO(4). Däremot måste naturligtvis utfallet av försök bli samma
oavsett om jag använt en beskrivning i SO(3,1) eller SO(4).
Om ljushastigheten är densamma i alla riktningar blir ljusstrålar raka. För att en ljusstråle skall
krökas måste ljushastigheten vara lägre längs innerkurvan än längs ytterkurvan. MM:s försök visade
att ljushastigheten INOM ett referenssystem är lika i alla riktningar. Av det kan man inte dra några
slutsatser som handlar om övergångar mellan referenssystem.
Jag kan inte komma från ett referenssystem till ett annat utan acceleration. Mellan två
referenssystem finns alltså ett accelerationsfält alltså ett gravitationsfält. Stjärnan vid
solförmörkelsen visar att ljuset böjs i solens gravitationsfält. Eftersom den enda kunskap vi har om
vad som finns på avstånd kommer från ljus och liknande fenomen som når oss ser vi inte om
ljusstrålar är raka eller krokiga. I en prismakikare är en ljusstråle långt ifrån rak men när vi tittar i
kikaren märker vi ingenting av dessa krokar.
Med raka ljusstrålar kan man bara se rakt. En ljusstråle längs x-axeln visar enbart vad som händer
på x-axeln. Man kan inte set runt ett hörn. Men en krokig ljusstråle kan ha varit inne i en annan
dimension. Om ljusstrålar kan vara krokiga kan det längs x-axeln komma en stråle som visar vad
som hänt på t-axeln. x-koordinaterna blir då inte helt oberoende av t-koordinaterna.
Hur skall man hantera att ljusstrålar böjs vid övergången mellan två referenssystem?
En möjlighet är att med en icke-ortogonal transform vrida rummet så att tidsaxeln får en
rumsprojektion. Man kan då använda koordinatsystem som särbehandlar tidskoordinaten SO(3,1).
En annan är att vrida hela koordinatsystemet. Då ändras vad som är tid och vad som är rum vilket
kräver att alla axlar betraktas som likvärda och utbytbara SO(4).
Relativitetsteorin beskriver ett sätt att transformera mellan SO(3,1)-system på sådant sätt att
ljusstrålar beskrivs som raka. Det betyder naturligtvis inte att de ÄR raka. Begreppen rak och krokig
hör till vår beskrivning av världen. Det är först när vi beskriver en ljusstråle som vi kan tala om rak
eller krokig.
Världen kan beskrivas i SO(3,1) eller SO(4) (och på andra sätt). Men beskrivningen blir olika och
man kan inte utan vidare ta samband från en beskrivning i SO(3,1) och använda dem i SO(4). Varje
beskrivning måste bygga på sina egna regler och övergång mellan beskrivningarna måste göras
med hjälp av regelövergångar.
__________________
2013-01-31
Då var det dags för längdkontraktion och tidsdilation i SO(4).
När Pelle springer genom ladan skall han se en kortare lada och jag skall se en Pelle som färdas
långsammare än jag i min koordinattidsriktning. Blir det så?
Sätt v/c till sin(a) och tolka (a) som vinkeln mellan min och Pelles koordinattidsaxlar. Då blir
lorentzkontraktionen cos(a). Och vinkeln mellan min och Pelles x-axel blir också (a). I Pelles system
får ladan en komposant i x-led och en komposant i t-led. x-komposanten blir ladans längd gånger
cos(a) (längdkontraktion) och t-komposanten blir ladans längd gånger sin(a).
När jag färdas T enheter längs min koordinattidsaxel färdas Pelle T enheter längs sin
koordinattidsaxel. Men eftersom Pelle delvis färdas i mitt rum, alltså i min x-riktning, kommer han att
färdas långsammare i min koordinattidsriktning. Han färdas bara Tcos(a) i min koordinattidsriktning
(tidsdilation) och i min x-riktning färdas han Tsin(a).
__________________
2013-02-01
Jag är naturligtvis medveten om att du kan ha rätt. Men om jag skall felförklara den avbildning som
människor använt i tusentals år och funnit användbar och pålitlig vill jag ha mycket påtagliga bevis.
Att man kan använda en annan avbildning är inte något bevis på att den gamla är fel Men - visst.
Jag tänker ibland på vilka konsekvenser det skulle ha men först vill jag veta hur jag kan använda den
gamla vanliga avbildningen.
Det är uppenbart att vi använder begreppet tid på sätt som vi inte kan använda rumskoordinater.
Som jag ser det beror det på att vi använder tid som ett sammanfattningsbegrepp för två olika
begrepp, parametertid och koordinattid. Parametertid är en skalär förändringsparameter,
koordinattiden är en koordinat av samma typ som rumskoordinaterna.
Om c är högsta möjliga hatighet och jag färdas med hastigheten c i koordinattidsled kan jag ju inte
röra mig fritt i koordinattidsled. Men det finns mycket att säga om detta. Jag skall försöka
återkomma.
Så vitt jag kunnat finna handlar alla MM-mätningar om mätningar inom ett referenssystem. Inga
delar av mätanordningarna rör sig i förhållande till varandra med hastigheter som närmar sig
ljushastighet. Då säger inte mätningarna något om övergångar mellan referenssystem.
Maxwells ekvationer säger inte alls att ljushastigheten är densamma i alla referenssystem. De säger
att ljushastigheten är ett genom roten ur produkten av det ljusbärande mediets
dielektricitetskonstant och magnetiska permeabilitet. Det är till exempel väl känt att ljushastigheten i
glas är lägre än i luft. Det är grunden för hela optiken. Och det handlar inte om att ljuset "studsar"
sig genom glaset. Vi kan mäta dielektricitetskonstant och magnetisk permeabilitet med metoder som
inte använder ljus och se att resultatet stämmer.
__________________
2013-02-01
Om avståndet mellan två punkter i euklidisk metrik är noll sammanfaller punkterna. Det är i så fall
en dubbelräkning av samma punkt. Det är ju detta som är innebörden i att avbildningen är bijektiv.
Man lägger aldrig två olika punkter med avståndet noll. Men detta gäller bara om man anger läget
med fyra koordinater. Det visste redan neandertalaren som kastade sten mot ett byte. Men vi
använder också tid som en förändringsparameter. Som jag ser det är det uppenbart att detta är två
olika sätt att använda tidsbegreppet. För mig är detta så självklart att jag har svårt att uttrycka det
tydligare.
Jag färdas med hastigheten c i min koordinattidsriktning. Jag kan varken röra mig fortare eller
långsammare. Men det intressanta är att Pelle kan färdas i en annan riktning. Och under vissa
förutsättningar kan han tala om vad han ser.
__________________
2013-20-02
Om världen är fyrdimensionell kan den avbildas bijektivt på en fyrdimensionell bild. Det betyder att
man till varje bildpunkt knyter en och endast en verklighetspunkt.
Både R^4 och R^(1,3) är fyrdimensionella och det går alltså att lägga en bijektiv bild på dem.
I stället för att lägga bijektiva bilder kan jag lägga en euklidisk bild på R^4 och en minkowskibild på
R^(1,3). Med euklidisk bild menar jag en bild där jag på varje bildpunkt lägger alla
verklighetspunkter med det euklidiska avståndet noll mellan sig. Och med minkowskibild menar jag
en bild där jag lägger alla verklighetspunkter med minkowskiavståndet noll mellan sig på samma
bildpunkt.
Om jag tar en verklighetspunkt så finns det inga andra verklighetspunkter på det euklidiska
avståndet noll. Den euklidiska bilden blir alltså bijektiv. Däremot finns det en grupp
verklighetspunkter som har minkowskiavståndet noll mellan sig. Minkowskibilden blir alltså inte
bijektiv. Jag kan inte återskapa verkligheten från minkowskibilden.
En regel som i den euklidiska bilden pekar ut en bildpunkt pekar entydigt ut en verklighetspunkt. En
regel som i minkowskibilden pekar ut en bildpunkt pekar ut en grupp verklighetspunkter. Detta är en
fundamental skillnad mellan regler i den euklidiska bilden och regler i minkowskibilden. Man kan
med matematiska metoder visa att bildernas regler är fundamentalt olika men det viktiga är att man
vet vari olikheten består.
När man i praktiken försöker använda minkowskibilden upptäcker man snart att den inte räcker. Man
behöver bara försöka följa fasläget i ett växelströmsnät eller räkna på fading mellan signaler med
olika gångväg eller bestämma position med hjälp av satelitklockor för att upptäcka att man måste
komplettera minkowskiavståndet med det euklidiska avståndet.
Jag kan naturligtvis komplettera minkowskibilden med den euklidiska bilden så att jag får en bijektiv
bild men då använder jag ju den euklidiska bilden.
Effekter på ljusstrålar och effekter av en påstådd eter är väl helt enkelt samma sak. Och jag ser
inget konstigt i att ett medium påverkas av acceleration.
Kausalitet är en stor fråga. Det behövs mer än några rader om det.
__________________
2013-02-03
Om jag gör en bijektiv avbildning (A) av verkligheten använder jag en regel som knyter varje
verklighetspunkt till en och endast en bildpunkt. Omvändningen av denna regel lägger tillbaka
bildpunkten på verklighetspunkten och återskapar alltså förlagan från bilden. Om jag så gör en
annan bijektiv bild (B) med en annan regel får jag två olika bilder. Om jag då tillämpar B:s regel på
omvändningen av A:s regel får jag en regel som avbildar A på B. Om två bilder är bijektiva
avbildningar av samma förlaga finns det alltså en regel som avbildar den ena på den andra.
Om världen är symmetrisk kan man dela in den i undergrupper där varje undergrupp har någon
gemensam egenskap. Om man inte är intresserad av förhållandena inom varje undergrupp kan man
använda en icke-bijektiv avbildning där varje bildpunkt inte svarar mot en verklighetspunkt utan mot
en sådan undergrupp.
Om världen har andra icke-materiella egenskaper kommer de inte med i någon form av avbildning.
De ligger alltså helt utanför den här diskussionen.
Jag färdas mot min framtid. Om jag inte gör något är min framtid Vendelsös framtid. Men om jag
tar bilen och kör mot Karlstad där min far bodde ändras min färdriktning så att min framtid blir
Karlstads framtid. Min färdriktning bildar alltså en vinkel med markens färdriktning. När jag ser på
min hastighetsmätare visar den sinus för denna vinkel. Jag brukar se det som att hastighetsmätaren
visar nanosinus som ju är ungefär samma som km/h. När hastighetsmätaren visar 90 färdas jag
alltså med 90 nanosinus mot Karlstads framtid. När jag kommer fram till Karlstads börjar jag lägga
Karlstads dåtid till min dåtid.
När min far levde ringde han ibland och berättade vad som hänt i Karlstad. Utan att min
koordinattidsaxel gått genom Karlstad kunde jag då lägga in en del av Karlstads dåtid i min dåtid.
Jag tror att de flesta människor ser detta som så självklart att det inte behöver formuleras. Men jag
tror att det är viktigt att göra det så att jag kan se mer i detalj på vad det innebär.
__________________
2013-02-03
Ja. Det är ju som du säger inledningsvis så att man kan se världen på olika sätt (olika metriker). En
fördel med att vrida koordinatsystemet med arcsin(v/c) är att när du kommer till 90 grader byter
tidsaxeln plats med en rumsaxel och om du fortsätter vridningen kommer tiden att gå bakåt sett från
en utomstående betraktare. För den som faller in i hålet blir däremot allt oförändrat. Frågan om hur
man beskriver ett fall in i ett svart hål var en anledning till att jag tyckte den beskrivningen var
intressant.
__________________
2013-02-04
PuffTheDragon har på https://www.flashback.org/sp37376762 en beskrivning av situationen vid ett
svart hål.
Om vi hittar ett svart hål inom räckhåll kommer vi att kunna skicka ett rymdskepp genom det. Vad
händer när skeppet passerar genom hålet?
Antag att det finns två instrument på skeppets instrumentbräda. Det ena är en radiostyrd klocka som
visar tid enligt ett atomur på Jorden och det andra är en avståndsmätare som visar avståndet från
Jorden. Före start är det lätt att se vilket som är avståndsmätare och vilket som är klocka. Klockan
går och avståndsmätaren står stilla. När skeppet tar fart börjar avståndsmätaren att gå och klockan
saktar in.
Skeppet får falla i fritt fall mot hålet. När det når händelsehorisonten har det kommit upp i
ljushastighet. Klockan har stannat men avståndsmätaren går på samma sätt som klockan gjorde
före start. Klocka och avståndsmätare ser alltså ut att ha bytt plats. En av mina rumsaxlar har blivit
skeppets koordinattidsaxel och min koordinattidsaxel har blivit en av skeppets rumsaxlar. Men
frånsett att instrumenten bytt plats märker besättningen ingenting av händelsehorisontpassagen.
Ombord på skeppet fungerar alla naturlagar som vanligt. Skeppets koordinatsystem har vridits i
förhållande till mitt koordinatsystem men det har inte genomgått några inre förändringar. En vanlig
klocka ombord på skeppet går som avståndsmätaren.
När skeppet kommit innanför händelsehorisonten börjar klockan på instrumentbrädan att gå
baklänges och avståndsmätaren saktar in. Skeppet kan nu inte längre kommunicera med Jorden
men för besättningen är allt annat som vanligt. Man fortsätter att skriva i loggboken. Man daterar
loggboken både efter instrumentbrädesklockan, avståndsmätaren och den vanliga klockan.
När skeppet passerat hålets centrum har det rörelseenergi nog att fortsätta ut ur hålet. När det på
nytt passerar händelsehorisonten kan det åter börja rapportera till Jorden. Vi kan då få veta något
om hur det ser ut inne i hålet.
__________________
2013-02-04
Världen i sig har inga koordinater. För att få koordinater som jag kan använda måste jag avbilda
världen på ett koordinatsystem. Vilken typ av koordinater jag då får beror på vilken typ av
koordinatsystem jag valt och vilken typ av avbildning jag använt.
Som jag ser det har jag fyra koordinataxlar varav en pekar mot min framtid. Om vi har en väg som
går mellan gården och handelsboden kan jag och min kompis gå mot handelsboden medan du går
mot gården. Min koordinattidsaxel pekar då mot handelsbodens framtid och din pekar mot gårdens
framtid. Mitt på vägen möts vi och konstaterar att våra framtider ligger mycket nära varandra men
att det finns en liten skillnad som gör att vi kommer att ha ett rumsavstånd när vi kommer fram.
Jag och allt i min närmaste omgivning färdas mot nästan samma framtid. Det innebär att det
vanligtvis är självklart vad som skall vara koordinattidsriktning. Men vad som är koordinattidsriktning
är inte en egenskap hos världen. För ett rymdskepp som passerar mig med en hastighet som ligger
nära ljushastighet kan det som för mig är rum vara koordinattid.
__________________
2013-02-06
Du har helt rätt i att R^4 , R^(3,1) och R^(2,2) alla är fyrdimensionella och alltså kan ta emot en
bijektiv bild av verkligheten. Om information kunde överföras med oändlig hastighet skulle det inte
spela någon roll om man separerade axlarna eller inte. Då kunde man hantera varje koordinat som
oberoende av de övriga. Men om det finns en maximal hastighet blir inte tid och rum alltid
oberoende av varandra. Om jag sänder en signal för att påverka en stjärna som ligger på
rumsavståndet en miljon ljusår tar det två miljoner år innan jag får veta resultatet. Stjärnan är
alltså avlägsen både i tid och rum. Och när man transformerar mellan system som rör sig i
förhållande till varandra får rumskoordinater tidsprojektioner och tvärtom. Frågan är då hur man
hanterar detta.
Om man har separerat en axel som tidsaxel kan man inte direkt vrida in den i rummet för att kunna
projicera rums- och tidskoordinater på varandra. Man behöver använda en icke-ortogonal transform
för att projicera rum och tid på varandra. Den fråga jag en gång i tiden ställde mig var: "Kan jag
inte i stället vrida det ortogonala systemet i R^4?" Det kan jag naturligtvis göra. Världen bryr sig inte
om hur jag avbildar den eller hur jag hanterar dess bild. Frågan är om jag kan tolka en sådan bild
på ett vettigt sätt. Jag har nu använt det här synsättet i några årtionden och inte funnit något som
talar mot det. Men det betyder naturligtvis inte att det är det enda rätta, bara att det ibland är
användbart.
När det gäller kausaliteten så menar jag att vi ibland använder tid som en förändringsparameter
alltså som ett sätt att ordna händelser i löpande följd. Som jag ser det har detta inte direkt med
läge att göra. Det är därför jag ser parametertiden som något annat än koordinattiden. Kausalitet
avgörs alltså av parametertid. Om det finns ett orsaksamband mellan två händelser är den med
lägst parametertid orsak.
När parametertiden går färdas jag längs min koordinattidsaxel. De punkter jag lämnar kallar jag
dåtid, den punkt där jag befinner mig kallar jag nu och de punkter som ligger framför mig kallar jag
framtid. Pelle som far förbi i ett rymdskepp gör likadant med sin koordinattidsaxel. Att det råkar vara
en av mina rumsaxlar är inget som han märker något av.
Om jag vill påverka en händelse på rumsavstånd måste jag skicka en påverkanssignal. Den punkt på
min koordinattidsaxel där jag gör det kallar jag händelsens påverkansnu. Den punkt på min
koordinattidsaxel där jag befinner mig vid den parametertid som händelsen inträffar vid kallar jag
händelsens samtidsnu. Den punkt på min koordinattidsaxel där jag befinner mig där
bekräftelsebilden av händelsen når mig kallar jag händelsens observationsnu. Vid händelsens
påverkansnu och observationsnu är minkowskiavståndet till händelsen noll.
Jag sätter v/c = sin(a) där (a) är min vridningsvinkel. Eftersom sin inte kan bli större än ett behöver
jag då ingen begränsning av vridningsvinkeln. Även vridning mer än 90 grader kan ges en tolkning
vilket kommer att bli aktuellt när vi någon gång i framtiden börjar färdas genom svarta hål.
Lika lite som koordinatsystemet finns i verkligheten finns vridningsvinkeln i verkligheten. Den är en
egenskap hos det koordinatsystem jag valt. Men skall man leta efter en känguru är det kanske där
man skall leta. Men det är inte lätt att hitta genomförbara experiment som kan visa vad som gäller.
För de hastigheter vi normalt hanterar är skillnaden mellan sin och tan inte mätbara.
__________________
2013-02-07
Jag vet inte hur man hanterar bilder men vi kanske återigen kan använda dbshw:s bild
 Den är bra även om en del av texten är irrelevant i det här fallet. (Som jag ser det borde den blå
texten vara "50m/0,99c" och den svarta "kortare än 50m/0,99c")
Jag sätter c lika med ett. Jag använder alltså samma enhet för tid och längd. Vi skall ju tolka bilden,
inte sortomvandla.
Den röda linjen genom A och C är min koordinattidsaxel och koordinattidsaxeln för ladans vänstra
ände. Den röda linjen genom B och D är koordinattidsaxeln för ladans högra ände. Den blå linjen
genom A och D är Pelles koordinattidsaxel. Vinkeln mellan min och Pelles koordinattidsaxlar, alltså
vikeln CAB, är (a).
När Pelle springer in i ladan finns jag , Pelle och ladans vänstra ände i A. Och ladans högra ände
finns i B. När parametertiden går färdas jag och ladans båda ändar längs våra koordinattidsaxlar så
att när Pelle kommer ut ur ladan befinner jag mig i C och ladan ligger längs den streckade linjen CD.
Pelles koordinattid går genom ladan. När han färdas längs sin koordinattidsaxel kommer han alltså
att färdas från ladans ena ände vid A till den andra änden vid D. Den blå linjen mellan A och D är
alltså Pelles koordinattid för loppet. Vi kan kalla beloppet av denna koordinattid för T. Om Pelle har
med sig ett stoppur som han håller i handen mäter stoppuret parametertiden under loppet. Pelle
sätter av stoppurets parametertid som koordinattid på sin koordinattidsaxel. T är alltså
parametertiden för loppet.
Ladans längd, det vill säga den streckade linjen CD, är Tsin(a). Dagen före loppet har vi mätt ladans
längd och enats om hur lång ladan är. Pelle tar nu Tsin(a) och dividerar med T enligt sitt stoppur
och kommer till att hastigheten var Tsin(a)/T = sin(a).
Projektionen av T på min koordinattidsaxel är Tcos(a). Genom att Pelle delvis sprang i min
rumsriktning rörde han sig långsammare i min koordinattidsriktning.
Mot detta kan man invända att Pelle tar ladans längd i mitt koordinatsystem och dividerar med tiden
i sitt koordinatsystem (det vill säga med parametertiden). Då kan man hävda att han skulle i stället
ta Tsin(a)/Tcos(a) = tan(a) alltså ladans längd i mitt koordinatsystem dividerat med T:s projektion
på min koordinattidsaxel. Men ett problem med detta är att punkten C inte motsvarar någon verklig
händelse. Om jag försöker mäta tiden med ett stoppur finns det ingenting som säger att jag skall
trycka på stopp vid C. Bilden av Pelle i ladans utgångsdörr har ännu inte nått mig. När ljuset som
visar att Pelle kommer ut når fram till mig kan jag trycka på stoppuret. Från den tid som stoppuret
då visar kan jag dra bort gångtiden för ljus från D till min koordinattidsaxel och konstatera att jag
borde ha tryckt vid C. Sträckan AC är alltså inte direkt uppmätbar utan bara något som kan beräknas
enligt vissa regler. Det innebär att tan(a) inte är ett invändningsfritt sätt att definiera hastighet.
Jag tror att de flesta människor som fick uppgiften att springa genom ladan med en viss hastighet
skulle göra som Pelle, det vill säga mäta upp ladans längd före loppet, springa genom ladan med ett
stoppur och beräkna hastigheten som den uppmätta längden dividerad med vad stoppuret visar. Det
vill säga Tsin(a)/T = sin(a).
Jag säger inte att det är något fel på minkowskimetriken. Bara att den ibland är otillräcklig och att
det finns andra sätt att beskriva världen.
__________________
2013-02-08
Frågan är: "Vad är en synkron klocka?".
På 1950-talet jobbade jag på Televerkets radiosektion. På den tiden var det aktuellt att navigera
med hjälp av radiofyrar. Så småningom kom stabilare klockor, satelliter och GPS men det gav en
intressant inblick i användning av synkrona klockor.
Jag ställer mig vi ladans vänstra ände med en klocka. Kalle ställer sig vid ladans högra ände med en
klocka. För att synkronisera våra klockor håller jag upp min så att Kalle ser den och kan ställa sin
klocka. Så springer Pelle. Jag noterar klockslaget när han springer in och Kalle noterar klockslaget
när han springer ut. Kalle rapporterar sitt klockslag till mig. Från Kalles klockslag drar jag mitt
klockslag och får en tid som motsvarar AC. Allt verkar fungera.
"Men," säger jag till Kalle "håll för säkerhets skull upp din klocka så att jag kan kontrollera att den
går rätt".
Kalle håller upp klockan och jag säger: "Den går för sakta. Den går fel med 2(50/c)."
"Nej den går exakt lika som din."
"Så här kan vi inte ha det."
"Jag vet. Vi tar två atomur, synkroniserar dem vid A och flyttar ett av dem till D. Vi kan ju låta Pelle
ta med uret. Han skall ju ändå från A till D."
"Men det är ju vad vi gjorde första gången. Pelles stoppur är av yppersta klass. Det går lika stabilt
som ett atomur."
Klockor mäter parametertid. Om vi använder Einsteins definition av längd och tid blir hastighet det
som vi mäter med en meterstav dividerat med det som vi mäter med en klocka alltså längd genom
parametertid.
__________________
2013-02-09
Det finns många synpunkter på synkronisering av klockor. Den artikel som du hänvisar till tar upp
några. Den synkroniseringsmetod du nämner innebär, som jag ser det, att du anser att klockorna
går synkront när de går i varandras samtidsnu. När Kalle och jag ser lika stora fel när vi tittar på
varandras klockor. Och du hävdar att hastighet är inte kvoten mellan det man mäter med en
meterstav dividerat med det man mäter med en klocka utan kvoten mellan det man mäter med en
meterstav och skillnaden mellan det man mäter med två klockor. Så kan man göra men jag vet inte
om det kan ses som helt självklart.
Innan vi i detalj diskuterar tolkning av bilden borde vi väl enas om att den är gjord på rätt sätt. Jag
tror att vi är överens om att om jag har ett läge angivet som tre rumskoordinater och en
tidskoordinat kan jag entydigt lägga in det i ett koordinatsystem enligt bilden. Det betyder att jag kan
lägga in punkterna A , B, C och D. Och det betyder att jag kommer att färdas genom A och C, Pelle
kommer att färdas genom A och D och Kalle genom B och D.
Jag tror att vi är överens fram till frågan om vad som är Pelles tidsaxel. Enligt dig är det inte den blå
linjen utan en axel som ligger mellan AC och AD med vinkeln (b) mot AC sådan att tan(b) = sin(a).
Du menar att om jag transformerar (a) till mitt referenssystem så får jag (b). Är det så?
Din vanliga invändning är att vi behöver inte alls använda den här bilden men som jag ser det är den
så självklar att vi alla, medvetet eller omedvetet, använder den och då kan man inte bara förneka
den. Fysik handlar om att beskriva och tolka upplevelser inklusive vardagsupplevelser.
__________________
2013-02-10
Först en synpunkt på val av referenssystem.
Vinkeln (a) är vinkeln MELLAN mitt och Pelles system. Den hör lika mycket till Pelles som till mitt
system. Den används för överföring mellan systemen. När jag använder (a) går jag alltså från det
ena systemet till det andra. När jag tar Pelles löptid gånger sin(a) innebär användningen av (a) att
jag tar resultatet till ladans längd i mitt system. Det är därför som det intuitivt känns rätt att göra så.
Så tar du upp den fråga som länge har bekymrat mig också. Hur går ljuset från en händelse fram till
mig? Jag vet fortfarande inte hur jag hanterar bilder men du har tydligen liksom jag konstaterat att
det borde gå i 45 grader mot t-axeln. Men då blir ju gångvägen längre än rumsavståndet. Det är här
jag behöver en eter. Om ljuset går vinkelrätt mot färdriktningen i en eter som följer med mig i t-
riktningen blir ljusets gångväg lika med rumsavståndet. Frågan blir då hur man hanterar övergångar
mellan olika referenssystem som alla har en medföljande eter. Men du kan aldrig gå mellan två
referenssystem som har en hastighet i förhållande till varandra utan att passera en
accelerationszon. Frågan blir då hur ljuset går genom en accelerationszon.
__________________
2013-02-14
Visst har ljus partikelegenskaper men inte när det gäller hastighet. Partiklar kan ha olika hastighet
men enligt Maxwells ekvationer är ljusets hastighet i förhållande till det ljusbärande mediet bestämd
av det ljusbärande mediets kapacitans och induktans.
När jag färdas längs min koordinattidsaxel följer ladan, marken där jag står och luften som omger
mig med mig. Det ligger då nära till hands att anta att även det ljusbärande medium som jag svävar
i följer med mig.
__________________
2013-02-17
Maxwells ekvationer kan ses som en generalisering av Kirchhoffs lagar. Kirchhoffs lagar handlar om
källfrihet och virvelfrihet. Maxwell generaliserade sambanden till att handla om källstyrka och
virvelstyrka. Elegant - särskilt om man tänker på att radiovågor var ett okänt begrepp på Maxwells
tid, men det är enkelt och rakt på sak.
Om jag skickar en signal på en telefonledning går den längs ledningen med en hastighet som
bestäms av ledningens kapacitans och induktans. Samma regler gäller om jag skickar en signal på
en glasfibertråd eller genom en glasbit eller genom vakum. Vakum kan alltså fungera som
referenssystem för signalens hastighet.
Om jag spelar biljard ombord på en båt som går med konstant hastighet fungerar biljardbordet som
mitt "utbredningsmedium". Alla lagar som styr bollarnas rörelse kan uttryckas med bordet som
referenssystem. Om jag vet båtens fart och riktning kan jag omvandla hastigheter i förhållande till
bordet till hastigheter i förhållande till omgivande vatten men det är inte dessa hastigheter jag
använder när jag skall beräkna en stöt mot en boll. Det är hastigheter i förhållande till det bord som
följer med mig som är användbara. Och c är en hastighet i förhållande till det medium som följer
med mig.
För partikelhastighet och vågutbredning kan man sätta partikelhastigheten lika med
grupphastigheten för en våg. Det leder till Schrödingerekvationen som man kan se som
telegrafekvationen för ett medium där kapacitans och induktans bestäms av partikelns
rörelseeneergi. Det innebär att man kan se massa som en egenskap hos mediet men det är värt en
egen mässa.
__________________
2013-02-19
Du har rätt i att man kan härleda ett specialfall från ett generellt samband men för att komma från
ett specialfall till ett generellt samband krävs mer än bara härledning. Jag ville bara påpeka att det
inte är något konstigt med Maxwells ekvationer.
Med hjälp av en universell hastighet kan man omvandla tidsenheter till längdenheter eller tvärtom.
Men vilken hastighet är den universella? Vi kan inte säga ljushastigheten eftersom det är uppenbart
att ljushastigheten är olika i olika material. Så vi försöker säga att det är ljushastigheten i vakuum.
Men därav kan vi inte dra slutsatsen att ljushastigheten i vakuum alltid är konstant. Jag menar att vi
måste gå minst ett steg till och säga att det är ljushastigheten i vakuum där det inte finns någon
gravitation. Du kan naturligtvis skriva Maxwells ekvationer för gravitationsfritt vakuum men då måste
du anpassa dem till det medium som du använder dem i.
När det gäller hastighet i 45 grader så är det som jag ser det inte fråga om en hastighet i
förhållande till ett utbredningsmedium och därmed inte ett problem.
Jag tror inte världen bryr sig om hur "man" härleder Schrödingerekvationen. Frågan är hur den kan
tolkas.
__________________
2013-02-21
Maxwells ekvationer är utmärkta verktyg för att hantera signaler i kraftledningar, telefonledningar,
glasfiberkablar, glaslinser, radiolänkar, radarsystem med mera. Jag har mycket sällan använt dem
för signaler i vakuum.
Frågan om universell hastighet är stor men jag skall försöka säga något om hur jag ser på den.
Det tycks finnas en egenskap hos världen att ett kvanta bara kan byta plats med intilliggande
kvantaposition. Jag antar att det är så. Varje gång ett kvanta byter plats med intilliggande
kvantaposition förändras världen. Jag kallar detta för en enhetshändelse och den inkrementerar
parametertiden. Om världen innehåller h kvanta kommer var h:te enhetshändelse att gälla ett visst
kvanta. Detta kvanta kan alltså förflytta sig en kvantaposition på h parametertidsenheter. Om alla
förflyttniingar sker i samma riktning förflyttar det sig då med hastigheten 1/h kvantapositioner per
parametertidsenhet. Detta är den högsta möjliga hastigheten. Jag definierar då hastighet som
förflyttning i ett utbredningsmedium (kvantapositionerna utgör ju ett utbredningsmedium) dividerat
med den parametertid som förflyttningen tar.
Men vi använder inte bara begreppet hastighet i betydelsen förflyttning per tidsenhet utan även i
betydelsen avståndsändring per tidsenhet. Vid till exempel siktesberäkning måste man använda
minst tre olika hastigheter. Hastighet i förhållande till målet, hastighet i förhållande till omgivande
luft och hastighet i förhållande till markkontrollen. Det är enbart hastigheten i förhållande till
omgivande luft som kan ses som förflyttning i utbredningsmediet (luft) dividerad med
parametertiden.
Som jag ser det är varje observatör en del av det medium som omsluter observatören.
__________________
2013-02-23
Jag utgår inte från fysikens beskrivning av världen. För mig är verkligheten den värld som jag
upplever med mina sinnen. I fysikboken hittar jag en beskrivning, alltså en karta över världen. Om
kartan inte stämmer med verkligheten gäller verkligheten. Men oftast stämmer kartan när man väl
lärt sig hur den skall tolkas.
Avbildningar kan göras på olika sätt. Att en avbildning är korrekt betyder inte att alla andra är fel.
Olika korrekta avbildningar kan framhäva olika egenskaper hos föremålet. Det är därför ofta
motiverat att använda flera avbildningar av samma föremål.
Jag säger inte att det är något fel på en avbildning med raka ljusstrålar. Jag säger bara att ibland
visar den inte det jag vill se och då vill jag ha en annan bild. Jag kan avbilda på vilket
koordinatsystem som helst. Världen påverkas inte av mitt sätt att avbilda den. Men när jag använder
bilden måste jag ta hänsyn till hur den är gjord.
Jag kan naturligtvis rita en bild på rutat papper och använda bilden enligt regler som motsvarar de
regler jag använde när jag ritade den.
För ALLA avbildningar gäller att en egenskap hos bilden kan vara en egenskap hos förlagan eller en
egenskap hos avbildningen. Att parallella linjer får V-form i en perspektivbild är inte en egenskap
hos förlagan utan en egenskap hos avbildningen. Trots det är perspektivbilder användbara.
Hela datatekniken bygger på insikten att man kan avbilda på binära tal. Det är en avbildning som har
visat oss en rad nya möjligheter.
Artikeln som du hänvisar till handlar om eventuella olinjariteter vid höga energinivåer. En intressant
fråga men den har mycket lite med val av koordinatsystem att göra.
__________________
2013-02-24
Två system A och B rör sig i förhållande till varandra. En observatör i A och en observatör i B
uppmäter samma ljushastighet i alla riktningar. Den slutsatsen kan man dra av MM:s försök. Det är
då uppenbart att en ljusstråle kan inte gå rakt mellan observatörerna i A och B. Men om man säger
att man bara kan gå mellan A och B via en icke-ortogonal transformation som vrider t-axeln i
förhållande till x-axeln kan man vrida ljusstrålen så att den blir rak.
Så kan man göra.
Ett annat sätt är att säga att man kan inte gå mellan A och B utan att passera en accelerationszon
som kröker ljusstrålar.
__________________
2013-02-24
Vem har sagt att vi pratar fysik? Gud Fader? Jag gör det inte. Jag försöker berätta lite om hur jag
hanterar den värld som omger mig. Och det handlar om olika sätt i olika sammanhang.
Ett exempel på en egenskap hos världen är färg. Jag hanterar färg antingen som ljusvåglängd eller
som RGB-värde med tre bytes per pixel eller som recept på brytfärger. Att ett av sätten ät rätt
betyder inte att de andra är fel. Jag använder alla tre sätten i olika sammanhang.
När det gäller val av koordinatsystem har vi alla en vana vid att använda ett reellt fyrdimensionellt
system. Det är inte så att vi enbart projicerar på ett tredimensionellt rum. Vi är mycket medvetna
om en fjärde koordinat när vi väntar i kön med vår kölapp. För hundra år sedan kompletterade vi
detta system med relativitetsteorins synsätt. Det gjorde att vi kunde se vissa samband tydligare men
det handlade trots allt bara om en liten del av den lilla del av min värld som kallas fysik. I vår vardag
använder vi, även du, vår gamla uppfattning om avstånd i tid och rum.
Men du har rätt i att det är viktigt att man tar reda på hur olika synsätt fungerar och hur de övergår i
varandra.
Hilbert lär ha ansett att Einstein var korkad eftersom han inte nöjde sig med ekvationer utan skulle
ha beskrivningar på vardagsspråk. Ett vanligt Einstein-citat är " Sen matematikerna fick hand om
relativitetsteorin förstår jag den inte själv.". Även om det var skämtsamt ligger det en insikt i det.
Ett matematiskt uttryck kan vara ett effektivt sätt att säga något men om man inte förstår
innebörden är det värdelöst.
__________________
2013-02-26
Det ligger en del i det du säger men det är inte hela sanningen.
Latin och matematik är ibland effektiva språk men en dumhet förblir en dumhet vilket språk man än
formulerar den på. Den insikt som gör att vi ibland kan se att kejsaren är naken måste bygga på
sunt bondförnuft. Hur mycket prästen än säger "Hoc est corpus" måste vi se att han håller en brödbit
i handen. Och hur mycket man än påstår att en krökt ljusstråle är rak i ett krökt rum måste vi se att
den är krökt i förhållande till rummet.
Jag skall försöka att mycket kortfattat antyda hur jag ser på Lorentztransformen.
När jag ser en stjärna är det ljus från stjärnan som når mig. Detta är den enda information om
stjärnan som når mig. Jag kan inte nå den på något annat sätt för att kolla hur ljuset från den har
gått för att komma fram till mig. Jag kan då anta att ljusstrålar är raka. I mitt närområde kan jag
jämföra bilder av föremål med andra sätt att nå dem och även om jag finner många exempel på
krökta ljusstrålar kan jag konstatera att ljusstrålar ofta är raka. Jag kan då använda raka ljusstrålar
som ett axiom och bygga en modell av världen med detta.
Ljus utbreder sig parallellt med mina rumsaxlar, till exempel x-axeln. Antag att jag befinner mig i
system A och ser på system B som rör sig i förhållande till A. Om jag vrider koordinatsystemet i B så
att B:s t-axel bildar en vinkel med min t-axel kommer även B:s x-axel att bilda en vinkel med min x-
axel. Raka ljusstrålar som utbreder sig i system B, alltså parallellt med B:s x-axel, kan då inte vara
parallella med min x-axel. Hur skall man hantera detta?
Som jag ser det finns det åtminstone två sätt. Antingen använder man en icke-ortogonal transform
(Lorentztransformen) som inte bevarar rät vinkel mellan t-axeln och x-axeln eller också låter man
ljusstrålarna krökas så att de når mig parallellt med min x-axel. Båda metoderna ger resultatet att
ljusstrålar i B är parallella med B:s x-axel och i A parallella med A:s x-axel. Vilket sätt man använder
är en fråga om hur man hanterar bilden. Förlagan påverkas inte av vilken metod man använder.
Om man nu använder metoden att arbeta med krökta ljusstrålar kan man naturligtvis "bevisa" att
det blir "fel" eftersom ljusstrålar blir krokiga. Men om man väljer en viss modell måste man
utvärdera den inom sig. Man får bara jämföra modelloberoende resultat.
Jag antar att din invändning är att vi bara behöver ett sätt att se på världen men jag tror att olika
sätt kan visa oss olika möjligheter. Det kan jag ju inte veta men jag tror att chansen är tillräcklig för
att det skall vara mödan värt.
Det här är ingen ny teori. Jag ser ju bara på min värld på det sätt som vi alltid har gjort.
__________________
2013-02-28
Om man släpper kravet att ljusstrålar skall vara raka kan en ljusstråle gå mellan Pelles och min
koordinattidsaxel via en cirkelbåge. En cirkel med centrum i origo är vinkelrät mot alla
koordinattidsaxlar som går genom origo. Om en foton går från (0,x) till (t=x,0) via en cirkelbåge blir
mitt rumsavstånd till fotonen roten ur (x^2 - t^2). Om man släpper förbudet mot att tala om en eter
kan man tillämpa hela strömningsläran på eterflödet och bland annat se gravitation som eterflödets
divergens.
Men det handlar inte om någon ny matematiskt formulerad teori. Bara om att se innebörden i
välkända samband. Jag försöker påpeka att jag bara berättar hur jag använder den världsbild jag
tror att vi alla känner igen. Att vi ibland använder tid som förändringsparameter och ibland som
koordinat och att jag försöker påpeka att vi borde skilja mellan begreppen parametertid och
koordinattid är inte heller någon ny teori, bara ett sätt att undvika en del missförstånd.
__________________
2013-03-05
Jag skall försöka beskriva hur koordinattid och rum fungerar.
När parametertiden går färdas jag med ljushastighet åt något håll i en fyrdimensionell rymd. Jag
lägger in ett fyraxligt, rätlinjigt, ortogonalt koordinatsystem och vrider det så att en av axlarna pekar
i min färdriktning. Den axeln kallar jag koordinattidsaxel eller t-axel. De övriga tre axlarna kallar jag
rumsaxlar eller x- , y-, z-axel. Jag kan alltså per definition aldrig lämna min koordinattidsaxel bara
färdas framåt längs den.
Via ljus som når mig kan jag se föremål på rumsavstånd. Om de färdas med samma hastighet som
jag gör blir deras rumskoordinater oförändrade och jag upplever att jag ligger stilla i rummet. Jag
kan nå en punkt som befinner sig på rumsavstånd genom att jag kan vrida min koordinattidsaxel så
att den pekar in i det som före vridningen var mitt rum. På det sättet kan jag alltså få min
koordinattidsaxel att gå genom punkten så att jag når den när jag färdas längs axeln.
För mig är koordinattiden speciell eftersom det är min färdriktning men för världen är det ingen
skillnad mellan rum och koordinattid. Om jag kunde vrida min koordinattidsaxel 90 grader skulle jag
kunna vrida den till min gamla x-axel som då skulle bli min nya koordinattidsaxel. Om jag kunde
skicka ett rymdskepp längs x-axeln skulle jag kunna beordra dem att uppnå ljushastighet så att
deras koordinattidsaxel blev min x-axel och be dem att berätta hur min koordinattidsaxel ser ut sedd
från sidan som en rumsaxel. Men dels förlorar jag möjligheten att kommunicera med skeppet när
det når ljushastighet dels kommer min koordinattidsaxel att ligga långt bort i deras dåtid.
Funderar man lite på detta blir det enkelt och självklart. Jag ser, som sagt, min hastighetsmätare
som om den visar nanosinus och när jag tar ett metersteg på en sekund känner jag hur
accelerationen vrider min koordinattidsaxel så att jag färdas en meter in i mitt gamla rum medan
jag färdas 300 000 km i koordinattidsled.
__________________
2013-03-07
Som fristående definitioner har jag svårt att få ut något av dem. Men vi är tydligen överens om att
man kan dela upp världen i smådelar. Även om man skulle kunna fortsätta uppdelningen i oändlighet
kan man ju då stanna vid någon nivå som man anser tillräcklig. Kanske redan på Planck-nivå men
jag tror att man bör utgå från Hubble-konstanten.
En koordinat har ingenting med kausalitet att göra. Att Uppsala ligger norr om Stockholm säger
ingenting om vad som är orsak och vad som är verkan. Det är därför som jag försöker påpeka att tid
är en sammanfattning av två olika begrepp. Dels en förändringsparameter (parametertid) dels en
koordinat (koordinattiden).
Parametertiden ordnar händelser i en följd på sådant sätt att en händelse inte kan vara orsak till
föregående händelser.
Koordinattiden anger läge i en fyrdimensionell värld. När parametertiden går ökar min koordinattid
på samma sätt som avståndet från avgångsstationen ökar när jag åker tåg men det betyder inte att
skillnaden mellan begreppen försvinner.
__________________
2013-03-09
Ett kort försök att sammanfatta grunden för mitt sätt att se på min värld.
Min värld är en värld som är tillräckligt stor och uppdelad i tillräcligt små kvanta. Den består av h
kvanta inordnade i H kvantapositioner. h och H är ändliga tal. H är grupperat i fyra dimensioner.
Ett kvanta kan bara ändra läge genom att byta plats med intilliggande tom kvantaposition. När detta
inträffar inträffar den minsta möjliga förändringen av min värld. Jag kallar detta för en
enhetshändelse. Varje gång (every time) en enhetshändelse inträffar inkrementeras en storhet som
jag kallar absolut tid. Absolut tid tilldelar alltså varje enhetshändelse ett unikt nummer. Just nu
anger absolut tid antalet enhetshändelser sedan tidens början (sedan gränsen för min värld). En
händelse kan inte vara orsak till händelser med lägre nummer, alltså lägre absolut tid. Skillnaden
mellan absolut tid för handelse A och händelse B kallar jag parametertiden mellan A och B.
Om jag betraktar ett visst kvanta gäller att det kommer att ändra läge var h:te gång en
enhetshändelse inträffar. Om kvantat enbart omges av tomma kvantapositioner kommer det varje
gång att förflytta sig i samma riktning. Det färdas alltså med hastigheten 1/h kvantapositioner per
enhetshändelse. Färdriktningen kallar jag kvantats koordinattidsriktning och förflyttningen kallar jag
kvantats koordinattid.
Observera att min värld är fyrdimensionell. Jag kan alltså lägga in fyra vinkelräta koordinataxlar x-,
y-, z- och t-axeln. Lägger jag t-axeln i kvantats koordinattidsriktning kommer det att ligga stilla i x-,
y-, och z-led.
Att parametertiden går innebär att händelser, som kan uppdelas i enhetshändelser, inträffar i min
värld. När mitt kvanta ändrar läge, alltså när koordinattiden för mitt kvanta ändras, vet jag att det
inträffat h enhetshändelser i min värld. Jag kan alltså använda mitt kvantas koordinattid som mått på
parametertiden. Om jag anger parametertiden i en enhet som är h enhetshändelser går mitt kvanta
en kvantaposition per parametertidsenhet så att beloppet av kvantats koordinattidsändring och
ändringen av parametertid blir lika. Detta har medfört en del problem när det gäller att se skillnaden
mellan begreppen men samma siffervärde betyder naturligtvis inte att begreppen är identiska.
Parametertid är en förändringsparameter som bland annat anger kausalitet. Koordinattid är en
koordinat som anger läge i en fyrdimensionell värld.
__________________
2013-03-11
Som jag ser det är det uppenbart att vi ibland använder "tid" som en förändringsparameter ibland
som en koordinat. Ett problem med ett sådant samlingsbegrepp är att om jag transformerar
tidskoordinaten transformerar jag även förändringsparametern. Tidskoordinaten blir då inte en
koordinat på samma sätt som rumskoordinaterna utan en storhet som måste särbehandlas.
Hur skall man kunna se tid som ett speciellt begrepp samtidigt som tidskoordinaten kan ha
rumsprojektioner? Minkowski föreslog en elegant lösning: Använd imaginär tid. Den är speciell men
blir reell när man kvadrerar den. Kvadraten kan alltså hanteras som andra koordinatkvadrater.
Ett annat sätt är att se parametertid och koordinattid som två olika begrepp.
Att se parametertid och koordinattid som olika begrepp kräver inte några nya matematiska
hjälpmedel. Det handlar bara om att hålla isär vad som är förändringsparameter och vad som är
koordinat. Och naturligtvis kan man fortfarande transformera dem som ett sammanfattande begrepp
men det viktiga är att man inte behöver göra det. Man kan transformera koordinattid som en
koordinat och parametertid som en parameter.
Den "matematik" som behövs är bara att man använder olika beteckningar för koordinattid och
parametertid. Jag brukar använda t för koordinattid och den grekiska bokstaven tao för
parametertid.
__________________
2013-03-14
Vi har alla gjort oss någon bild av den värld vi lever i. Jag tror att det kunde vara intressant att
utbyta lite erfarenheter av att använda dessa bilder. Därför berättar jag lite om min bild. Den som så
vill kan ju ibland tänka tanken: "Är detta en förändringsparameter eller en koordinat?". Kanske kan
någon se någon ny möjlighet. Bra eller dåligt? Tja det kan man ju inte säga i förväg.
Jag håller med dig om att man bör ta reda på hur den gängse världsbilden ser ut, om inte annat så
för att kunna ifrågasätta den. Och det kan också vara bra att känna till en del matematik. En vacker
dag kanske man behöver Christoffel¨s symboler eller Laplacetransformen och då kan det vara bra
att veta att de finns genomtänkta och färdiga att använda.
Naturligtvis kan man, som med Lorentztransformen, vrida x-axeln mot t-axeln så att de möts vid 45
grader bara man vet vad man gör och vet vad man skall ha resultatet till. Jag försöker bara påpeka
att det är inte det enda möjliga synsättet.
__________________
Den är bra även om en del av texten är irrelevant i det här fallet. (Som jag ser det borde den blå
texten vara "50m/0,99c" och den svarta "kortare än 50m/0,99c")
Jag sätter c lika med ett. Jag använder alltså samma enhet för tid och längd. Vi skall ju tolka bilden,
inte sortomvandla.
Den röda linjen genom A och C är min koordinattidsaxel och koordinattidsaxeln för ladans vänstra
ände. Den röda linjen genom B och D är koordinattidsaxeln för ladans högra ände. Den blå linjen
genom A och D är Pelles koordinattidsaxel. Vinkeln mellan min och Pelles koordinattidsaxlar, alltså
vikeln CAB, är (a).
När Pelle springer in i ladan finns jag , Pelle och ladans vänstra ände i A. Och ladans högra ände
finns i B. När parametertiden går färdas jag och ladans båda ändar längs våra koordinattidsaxlar så
att när Pelle kommer ut ur ladan befinner jag mig i C och ladan ligger längs den streckade linjen CD.
Pelles koordinattid går genom ladan. När han färdas längs sin koordinattidsaxel kommer han alltså
att färdas från ladans ena ände vid A till den andra änden vid D. Den blå linjen mellan A och D är
alltså Pelles koordinattid för loppet. Vi kan kalla beloppet av denna koordinattid för T. Om Pelle har
med sig ett stoppur som han håller i handen mäter stoppuret parametertiden under loppet. Pelle
sätter av stoppurets parametertid som koordinattid på sin koordinattidsaxel. T är alltså
parametertiden för loppet.
Ladans längd, det vill säga den streckade linjen CD, är Tsin(a). Dagen före loppet har vi mätt ladans
längd och enats om hur lång ladan är. Pelle tar nu Tsin(a) och dividerar med T enligt sitt stoppur
och kommer till att hastigheten var Tsin(a)/T = sin(a).
Projektionen av T på min koordinattidsaxel är Tcos(a). Genom att Pelle delvis sprang i min
rumsriktning rörde han sig långsammare i min koordinattidsriktning.
Mot detta kan man invända att Pelle tar ladans längd i mitt koordinatsystem och dividerar med tiden
i sitt koordinatsystem (det vill säga med parametertiden). Då kan man hävda att han skulle i stället
ta Tsin(a)/Tcos(a) = tan(a) alltså ladans längd i mitt koordinatsystem dividerat med T:s projektion
på min koordinattidsaxel. Men ett problem med detta är att punkten C inte motsvarar någon verklig
händelse. Om jag försöker mäta tiden med ett stoppur finns det ingenting som säger att jag skall
trycka på stopp vid C. Bilden av Pelle i ladans utgångsdörr har ännu inte nått mig. När ljuset som
visar att Pelle kommer ut når fram till mig kan jag trycka på stoppuret. Från den tid som stoppuret
då visar kan jag dra bort gångtiden för ljus från D till min koordinattidsaxel och konstatera att jag
borde ha tryckt vid C. Sträckan AC är alltså inte direkt uppmätbar utan bara något som kan beräknas
enligt vissa regler. Det innebär att tan(a) inte är ett invändningsfritt sätt att definiera hastighet.
Jag tror att de flesta människor som fick uppgiften att springa genom ladan med en viss hastighet
skulle göra som Pelle, det vill säga mäta upp ladans längd före loppet, springa genom ladan med ett
stoppur och beräkna hastigheten som den uppmätta längden dividerad med vad stoppuret visar. Det
vill säga Tsin(a)/T = sin(a).
Jag säger inte att det är något fel på minkowskimetriken. Bara att den ibland är otillräcklig och att
det finns andra sätt att beskriva världen.
__________________
2013-02-08
Frågan är: "Vad är en synkron klocka?".
På 1950-talet jobbade jag på Televerkets radiosektion. På den tiden var det aktuellt att navigera
med hjälp av radiofyrar. Så småningom kom stabilare klockor, satelliter och GPS men det gav en
intressant inblick i användning av synkrona klockor.
Jag ställer mig vi ladans vänstra ände med en klocka. Kalle ställer sig vid ladans högra ände med en
klocka. För att synkronisera våra klockor håller jag upp min så att Kalle ser den och kan ställa sin
klocka. Så springer Pelle. Jag noterar klockslaget när han springer in och Kalle noterar klockslaget
när han springer ut. Kalle rapporterar sitt klockslag till mig. Från Kalles klockslag drar jag mitt
klockslag och får en tid som motsvarar AC. Allt verkar fungera.
"Men," säger jag till Kalle "håll för säkerhets skull upp din klocka så att jag kan kontrollera att den
går rätt".
Kalle håller upp klockan och jag säger: "Den går för sakta. Den går fel med 2(50/c)."
"Nej den går exakt lika som din."
"Så här kan vi inte ha det."
"Jag vet. Vi tar två atomur, synkroniserar dem vid A och flyttar ett av dem till D. Vi kan ju låta Pelle
ta med uret. Han skall ju ändå från A till D."
"Men det är ju vad vi gjorde första gången. Pelles stoppur är av yppersta klass. Det går lika stabilt
som ett atomur."
Klockor mäter parametertid. Om vi använder Einsteins definition av längd och tid blir hastighet det
som vi mäter med en meterstav dividerat med det som vi mäter med en klocka alltså längd genom
parametertid.
__________________
2013-02-09
Det finns många synpunkter på synkronisering av klockor. Den artikel som du hänvisar till tar upp
några. Den synkroniseringsmetod du nämner innebär, som jag ser det, att du anser att klockorna
går synkront när de går i varandras samtidsnu. När Kalle och jag ser lika stora fel när vi tittar på
varandras klockor. Och du hävdar att hastighet är inte kvoten mellan det man mäter med en
meterstav dividerat med det man mäter med en klocka utan kvoten mellan det man mäter med en
meterstav och skillnaden mellan det man mäter med två klockor. Så kan man göra men jag vet inte
om det kan ses som helt självklart.
Innan vi i detalj diskuterar tolkning av bilden borde vi väl enas om att den är gjord på rätt sätt. Jag
tror att vi är överens om att om jag har ett läge angivet som tre rumskoordinater och en
tidskoordinat kan jag entydigt lägga in det i ett koordinatsystem enligt bilden. Det betyder att jag kan
lägga in punkterna A , B, C och D. Och det betyder att jag kommer att färdas genom A och C, Pelle
kommer att färdas genom A och D och Kalle genom B och D.
Jag tror att vi är överens fram till frågan om vad som är Pelles tidsaxel. Enligt dig är det inte den blå
linjen utan en axel som ligger mellan AC och AD med vinkeln (b) mot AC sådan att tan(b) = sin(a).
Du menar att om jag transformerar (a) till mitt referenssystem så får jag (b). Är det så?
Din vanliga invändning är att vi behöver inte alls använda den här bilden men som jag ser det är den
så självklar att vi alla, medvetet eller omedvetet, använder den och då kan man inte bara förneka
den. Fysik handlar om att beskriva och tolka upplevelser inklusive vardagsupplevelser.
__________________
2013-02-10
Först en synpunkt på val av referenssystem.
Vinkeln (a) är vinkeln MELLAN mitt och Pelles system. Den hör lika mycket till Pelles som till mitt
system. Den används för överföring mellan systemen. När jag använder (a) går jag alltså från det
ena systemet till det andra. När jag tar Pelles löptid gånger sin(a) innebär användningen av (a) att
jag tar resultatet till ladans längd i mitt system. Det är därför som det intuitivt känns rätt att göra så.
Så tar du upp den fråga som länge har bekymrat mig också. Hur går ljuset från en händelse fram till
mig? Jag vet fortfarande inte hur jag hanterar bilder men du har tydligen liksom jag konstaterat att
det borde gå i 45 grader mot t-axeln. Men då blir ju gångvägen längre än rumsavståndet. Det är här
jag behöver en eter. Om ljuset går vinkelrätt mot färdriktningen i en eter som följer med mig i t-
riktningen blir ljusets gångväg lika med rumsavståndet. Frågan blir då hur man hanterar övergångar
mellan olika referenssystem som alla har en medföljande eter. Men du kan aldrig gå mellan två
referenssystem som har en hastighet i förhållande till varandra utan att passera en
accelerationszon. Frågan blir då hur ljuset går genom en accelerationszon.
__________________
2013-02-14
Visst har ljus partikelegenskaper men inte när det gäller hastighet. Partiklar kan ha olika hastighet
men enligt Maxwells ekvationer är ljusets hastighet i förhållande till det ljusbärande mediet bestämd
av det ljusbärande mediets kapacitans och induktans.
När jag färdas längs min koordinattidsaxel följer ladan, marken där jag står och luften som omger
mig med mig. Det ligger då nära till hands att anta att även det ljusbärande medium som jag svävar
i följer med mig.
__________________
2013-02-17
Maxwells ekvationer kan ses som en generalisering av Kirchhoffs lagar. Kirchhoffs lagar handlar om
källfrihet och virvelfrihet. Maxwell generaliserade sambanden till att handla om källstyrka och
virvelstyrka. Elegant - särskilt om man tänker på att radiovågor var ett okänt begrepp på Maxwells
tid, men det är enkelt och rakt på sak.
Om jag skickar en signal på en telefonledning går den längs ledningen med en hastighet som
bestäms av ledningens kapacitans och induktans. Samma regler gäller om jag skickar en signal på
en glasfibertråd eller genom en glasbit eller genom vakum. Vakum kan alltså fungera som
referenssystem för signalens hastighet.
Om jag spelar biljard ombord på en båt som går med konstant hastighet fungerar biljardbordet som
mitt "utbredningsmedium". Alla lagar som styr bollarnas rörelse kan uttryckas med bordet som
referenssystem. Om jag vet båtens fart och riktning kan jag omvandla hastigheter i förhållande till
bordet till hastigheter i förhållande till omgivande vatten men det är inte dessa hastigheter jag
använder när jag skall beräkna en stöt mot en boll. Det är hastigheter i förhållande till det bord som
följer med mig som är användbara. Och c är en hastighet i förhållande till det medium som följer
med mig.
För partikelhastighet och vågutbredning kan man sätta partikelhastigheten lika med
grupphastigheten för en våg. Det leder till Schrödingerekvationen som man kan se som
telegrafekvationen för ett medium där kapacitans och induktans bestäms av partikelns
rörelseeneergi. Det innebär att man kan se massa som en egenskap hos mediet men det är värt en
egen mässa.
__________________
2013-02-19
Du har rätt i att man kan härleda ett specialfall från ett generellt samband men för att komma från
ett specialfall till ett generellt samband krävs mer än bara härledning. Jag ville bara påpeka att det
inte är något konstigt med Maxwells ekvationer.
Med hjälp av en universell hastighet kan man omvandla tidsenheter till längdenheter eller tvärtom.
Men vilken hastighet är den universella? Vi kan inte säga ljushastigheten eftersom det är uppenbart
att ljushastigheten är olika i olika material. Så vi försöker säga att det är ljushastigheten i vakuum.
Men därav kan vi inte dra slutsatsen att ljushastigheten i vakuum alltid är konstant. Jag menar att vi
måste gå minst ett steg till och säga att det är ljushastigheten i vakuum där det inte finns någon
gravitation. Du kan naturligtvis skriva Maxwells ekvationer för gravitationsfritt vakuum men då måste
du anpassa dem till det medium som du använder dem i.
När det gäller hastighet i 45 grader så är det som jag ser det inte fråga om en hastighet i
förhållande till ett utbredningsmedium och därmed inte ett problem.
Jag tror inte världen bryr sig om hur "man" härleder Schrödingerekvationen. Frågan är hur den kan
tolkas.
__________________
2013-02-21
Maxwells ekvationer är utmärkta verktyg för att hantera signaler i kraftledningar, telefonledningar,
glasfiberkablar, glaslinser, radiolänkar, radarsystem med mera. Jag har mycket sällan använt dem
för signaler i vakuum.
Frågan om universell hastighet är stor men jag skall försöka säga något om hur jag ser på den.
Det tycks finnas en egenskap hos världen att ett kvanta bara kan byta plats med intilliggande
kvantaposition. Jag antar att det är så. Varje gång ett kvanta byter plats med intilliggande
kvantaposition förändras världen. Jag kallar detta för en enhetshändelse och den inkrementerar
parametertiden. Om världen innehåller h kvanta kommer var h:te enhetshändelse att gälla ett visst
kvanta. Detta kvanta kan alltså förflytta sig en kvantaposition på h parametertidsenheter. Om alla
förflyttniingar sker i samma riktning förflyttar det sig då med hastigheten 1/h kvantapositioner per
parametertidsenhet. Detta är den högsta möjliga hastigheten. Jag definierar då hastighet som
förflyttning i ett utbredningsmedium (kvantapositionerna utgör ju ett utbredningsmedium) dividerat
med den parametertid som förflyttningen tar.
Men vi använder inte bara begreppet hastighet i betydelsen förflyttning per tidsenhet utan även i
betydelsen avståndsändring per tidsenhet. Vid till exempel siktesberäkning måste man använda
minst tre olika hastigheter. Hastighet i förhållande till målet, hastighet i förhållande till omgivande
luft och hastighet i förhållande till markkontrollen. Det är enbart hastigheten i förhållande till
omgivande luft som kan ses som förflyttning i utbredningsmediet (luft) dividerad med
parametertiden.
Som jag ser det är varje observatör en del av det medium som omsluter observatören.
__________________
2013-02-23
Jag utgår inte från fysikens beskrivning av världen. För mig är verkligheten den värld som jag
upplever med mina sinnen. I fysikboken hittar jag en beskrivning, alltså en karta över världen. Om
kartan inte stämmer med verkligheten gäller verkligheten. Men oftast stämmer kartan när man väl
lärt sig hur den skall tolkas.
Avbildningar kan göras på olika sätt. Att en avbildning är korrekt betyder inte att alla andra är fel.
Olika korrekta avbildningar kan framhäva olika egenskaper hos föremålet. Det är därför ofta
motiverat att använda flera avbildningar av samma föremål.
Jag säger inte att det är något fel på en avbildning med raka ljusstrålar. Jag säger bara att ibland
visar den inte det jag vill se och då vill jag ha en annan bild. Jag kan avbilda på vilket
koordinatsystem som helst. Världen påverkas inte av mitt sätt att avbilda den. Men när jag använder
bilden måste jag ta hänsyn till hur den är gjord.
Jag kan naturligtvis rita en bild på rutat papper och använda bilden enligt regler som motsvarar de
regler jag använde när jag ritade den.
För ALLA avbildningar gäller att en egenskap hos bilden kan vara en egenskap hos förlagan eller en
egenskap hos avbildningen. Att parallella linjer får V-form i en perspektivbild är inte en egenskap
hos förlagan utan en egenskap hos avbildningen. Trots det är perspektivbilder användbara.
Hela datatekniken bygger på insikten att man kan avbilda på binära tal. Det är en avbildning som har
visat oss en rad nya möjligheter.
Artikeln som du hänvisar till handlar om eventuella olinjariteter vid höga energinivåer. En intressant
fråga men den har mycket lite med val av koordinatsystem att göra.
__________________
2013-02-24
Två system A och B rör sig i förhållande till varandra. En observatör i A och en observatör i B
uppmäter samma ljushastighet i alla riktningar. Den slutsatsen kan man dra av MM:s försök. Det är
då uppenbart att en ljusstråle kan inte gå rakt mellan observatörerna i A och B. Men om man säger
att man bara kan gå mellan A och B via en icke-ortogonal transformation som vrider t-axeln i
förhållande till x-axeln kan man vrida ljusstrålen så att den blir rak.
Så kan man göra.
Ett annat sätt är att säga att man kan inte gå mellan A och B utan att passera en accelerationszon
som kröker ljusstrålar.
__________________
2013-02-24
Vem har sagt att vi pratar fysik? Gud Fader? Jag gör det inte. Jag försöker berätta lite om hur jag
hanterar den värld som omger mig. Och det handlar om olika sätt i olika sammanhang.
Ett exempel på en egenskap hos världen är färg. Jag hanterar färg antingen som ljusvåglängd eller
som RGB-värde med tre bytes per pixel eller som recept på brytfärger. Att ett av sätten ät rätt
betyder inte att de andra är fel. Jag använder alla tre sätten i olika sammanhang.
När det gäller val av koordinatsystem har vi alla en vana vid att använda ett reellt fyrdimensionellt
system. Det är inte så att vi enbart projicerar på ett tredimensionellt rum. Vi är mycket medvetna
om en fjärde koordinat när vi väntar i kön med vår kölapp. För hundra år sedan kompletterade vi
detta system med relativitetsteorins synsätt. Det gjorde att vi kunde se vissa samband tydligare men
det handlade trots allt bara om en liten del av den lilla del av min värld som kallas fysik. I vår vardag
använder vi, även du, vår gamla uppfattning om avstånd i tid och rum.
Men du har rätt i att det är viktigt att man tar reda på hur olika synsätt fungerar och hur de övergår i
varandra.
Hilbert lär ha ansett att Einstein var korkad eftersom han inte nöjde sig med ekvationer utan skulle
ha beskrivningar på vardagsspråk. Ett vanligt Einstein-citat är " Sen matematikerna fick hand om
relativitetsteorin förstår jag den inte själv.". Även om det var skämtsamt ligger det en insikt i det.
Ett matematiskt uttryck kan vara ett effektivt sätt att säga något men om man inte förstår
innebörden är det värdelöst.
__________________
2013-02-26
Det ligger en del i det du säger men det är inte hela sanningen.
Latin och matematik är ibland effektiva språk men en dumhet förblir en dumhet vilket språk man än
formulerar den på. Den insikt som gör att vi ibland kan se att kejsaren är naken måste bygga på
sunt bondförnuft. Hur mycket prästen än säger "Hoc est corpus" måste vi se att han håller en brödbit
i handen. Och hur mycket man än påstår att en krökt ljusstråle är rak i ett krökt rum måste vi se att
den är krökt i förhållande till rummet.
Jag skall försöka att mycket kortfattat antyda hur jag ser på Lorentztransformen.
När jag ser en stjärna är det ljus från stjärnan som når mig. Detta är den enda information om
stjärnan som når mig. Jag kan inte nå den på något annat sätt för att kolla hur ljuset från den har
gått för att komma fram till mig. Jag kan då anta att ljusstrålar är raka. I mitt närområde kan jag
jämföra bilder av föremål med andra sätt att nå dem och även om jag finner många exempel på
krökta ljusstrålar kan jag konstatera att ljusstrålar ofta är raka. Jag kan då använda raka ljusstrålar
som ett axiom och bygga en modell av världen med detta.
Ljus utbreder sig parallellt med mina rumsaxlar, till exempel x-axeln. Antag att jag befinner mig i
system A och ser på system B som rör sig i förhållande till A. Om jag vrider koordinatsystemet i B så
att B:s t-axel bildar en vinkel med min t-axel kommer även B:s x-axel att bilda en vinkel med min x-
axel. Raka ljusstrålar som utbreder sig i system B, alltså parallellt med B:s x-axel, kan då inte vara
parallella med min x-axel. Hur skall man hantera detta?
Som jag ser det finns det åtminstone två sätt. Antingen använder man en icke-ortogonal transform
(Lorentztransformen) som inte bevarar rät vinkel mellan t-axeln och x-axeln eller också låter man
ljusstrålarna krökas så att de når mig parallellt med min x-axel. Båda metoderna ger resultatet att
ljusstrålar i B är parallella med B:s x-axel och i A parallella med A:s x-axel. Vilket sätt man använder
är en fråga om hur man hanterar bilden. Förlagan påverkas inte av vilken metod man använder.
Om man nu använder metoden att arbeta med krökta ljusstrålar kan man naturligtvis "bevisa" att
det blir "fel" eftersom ljusstrålar blir krokiga. Men om man väljer en viss modell måste man
utvärdera den inom sig. Man får bara jämföra modelloberoende resultat.
Jag antar att din invändning är att vi bara behöver ett sätt att se på världen men jag tror att olika
sätt kan visa oss olika möjligheter. Det kan jag ju inte veta men jag tror att chansen är tillräcklig för
att det skall vara mödan värt.
Det här är ingen ny teori. Jag ser ju bara på min värld på det sätt som vi alltid har gjort.
__________________
2013-02-28
Om man släpper kravet att ljusstrålar skall vara raka kan en ljusstråle gå mellan Pelles och min
koordinattidsaxel via en cirkelbåge. En cirkel med centrum i origo är vinkelrät mot alla
koordinattidsaxlar som går genom origo. Om en foton går från (0,x) till (t=x,0) via en cirkelbåge blir
mitt rumsavstånd till fotonen roten ur (x^2 - t^2). Om man släpper förbudet mot att tala om en eter
kan man tillämpa hela strömningsläran på eterflödet och bland annat se gravitation som eterflödets
divergens.
Men det handlar inte om någon ny matematiskt formulerad teori. Bara om att se innebörden i
välkända samband. Jag försöker påpeka att jag bara berättar hur jag använder den världsbild jag
tror att vi alla känner igen. Att vi ibland använder tid som förändringsparameter och ibland som
koordinat och att jag försöker påpeka att vi borde skilja mellan begreppen parametertid och
koordinattid är inte heller någon ny teori, bara ett sätt att undvika en del missförstånd.
__________________
2013-03-05
Jag skall försöka beskriva hur koordinattid och rum fungerar.
När parametertiden går färdas jag med ljushastighet åt något håll i en fyrdimensionell rymd. Jag
lägger in ett fyraxligt, rätlinjigt, ortogonalt koordinatsystem och vrider det så att en av axlarna pekar
i min färdriktning. Den axeln kallar jag koordinattidsaxel eller t-axel. De övriga tre axlarna kallar jag
rumsaxlar eller x- , y-, z-axel. Jag kan alltså per definition aldrig lämna min koordinattidsaxel bara
färdas framåt längs den.
Via ljus som når mig kan jag se föremål på rumsavstånd. Om de färdas med samma hastighet som
jag gör blir deras rumskoordinater oförändrade och jag upplever att jag ligger stilla i rummet. Jag
kan nå en punkt som befinner sig på rumsavstånd genom att jag kan vrida min koordinattidsaxel så
att den pekar in i det som före vridningen var mitt rum. På det sättet kan jag alltså få min
koordinattidsaxel att gå genom punkten så att jag når den när jag färdas längs axeln.
För mig är koordinattiden speciell eftersom det är min färdriktning men för världen är det ingen
skillnad mellan rum och koordinattid. Om jag kunde vrida min koordinattidsaxel 90 grader skulle jag
kunna vrida den till min gamla x-axel som då skulle bli min nya koordinattidsaxel. Om jag kunde
skicka ett rymdskepp längs x-axeln skulle jag kunna beordra dem att uppnå ljushastighet så att
deras koordinattidsaxel blev min x-axel och be dem att berätta hur min koordinattidsaxel ser ut sedd
från sidan som en rumsaxel. Men dels förlorar jag möjligheten att kommunicera med skeppet när
det når ljushastighet dels kommer min koordinattidsaxel att ligga långt bort i deras dåtid.
Funderar man lite på detta blir det enkelt och självklart. Jag ser, som sagt, min hastighetsmätare
som om den visar nanosinus och när jag tar ett metersteg på en sekund känner jag hur
accelerationen vrider min koordinattidsaxel så att jag färdas en meter in i mitt gamla rum medan
jag färdas 300 000 km i koordinattidsled.
__________________
2013-03-07
Som fristående definitioner har jag svårt att få ut något av dem. Men vi är tydligen överens om att
man kan dela upp världen i smådelar. Även om man skulle kunna fortsätta uppdelningen i oändlighet
kan man ju då stanna vid någon nivå som man anser tillräcklig. Kanske redan på Planck-nivå men
jag tror att man bör utgå från Hubble-konstanten.
En koordinat har ingenting med kausalitet att göra. Att Uppsala ligger norr om Stockholm säger
ingenting om vad som är orsak och vad som är verkan. Det är därför som jag försöker påpeka att tid
är en sammanfattning av två olika begrepp. Dels en förändringsparameter (parametertid) dels en
koordinat (koordinattiden).
Parametertiden ordnar händelser i en följd på sådant sätt att en händelse inte kan vara orsak till
föregående händelser.
Koordinattiden anger läge i en fyrdimensionell värld. När parametertiden går ökar min koordinattid
på samma sätt som avståndet från avgångsstationen ökar när jag åker tåg men det betyder inte att
skillnaden mellan begreppen försvinner.
__________________
2013-03-09
Ett kort försök att sammanfatta grunden för mitt sätt att se på min värld.
Min värld är en värld som är tillräckligt stor och uppdelad i tillräcligt små kvanta. Den består av h
kvanta inordnade i H kvantapositioner. h och H är ändliga tal. H är grupperat i fyra dimensioner.
Ett kvanta kan bara ändra läge genom att byta plats med intilliggande tom kvantaposition. När detta
inträffar inträffar den minsta möjliga förändringen av min värld. Jag kallar detta för en
enhetshändelse. Varje gång (every time) en enhetshändelse inträffar inkrementeras en storhet som
jag kallar absolut tid. Absolut tid tilldelar alltså varje enhetshändelse ett unikt nummer. Just nu
anger absolut tid antalet enhetshändelser sedan tidens början (sedan gränsen för min värld). En
händelse kan inte vara orsak till händelser med lägre nummer, alltså lägre absolut tid. Skillnaden
mellan absolut tid för handelse A och händelse B kallar jag parametertiden mellan A och B.
Om jag betraktar ett visst kvanta gäller att det kommer att ändra läge var h:te gång en
enhetshändelse inträffar. Om kvantat enbart omges av tomma kvantapositioner kommer det varje
gång att förflytta sig i samma riktning. Det färdas alltså med hastigheten 1/h kvantapositioner per
enhetshändelse. Färdriktningen kallar jag kvantats koordinattidsriktning och förflyttningen kallar jag
kvantats koordinattid.
Observera att min värld är fyrdimensionell. Jag kan alltså lägga in fyra vinkelräta koordinataxlar x-,
y-, z- och t-axeln. Lägger jag t-axeln i kvantats koordinattidsriktning kommer det att ligga stilla i x-,
y-, och z-led.
Att parametertiden går innebär att händelser, som kan uppdelas i enhetshändelser, inträffar i min
värld. När mitt kvanta ändrar läge, alltså när koordinattiden för mitt kvanta ändras, vet jag att det
inträffat h enhetshändelser i min värld. Jag kan alltså använda mitt kvantas koordinattid som mått på
parametertiden. Om jag anger parametertiden i en enhet som är h enhetshändelser går mitt kvanta
en kvantaposition per parametertidsenhet så att beloppet av kvantats koordinattidsändring och
ändringen av parametertid blir lika. Detta har medfört en del problem när det gäller att se skillnaden
mellan begreppen men samma siffervärde betyder naturligtvis inte att begreppen är identiska.
Parametertid är en förändringsparameter som bland annat anger kausalitet. Koordinattid är en
koordinat som anger läge i en fyrdimensionell värld.
__________________
2013-03-11
Som jag ser det är det uppenbart att vi ibland använder "tid" som en förändringsparameter ibland
som en koordinat. Ett problem med ett sådant samlingsbegrepp är att om jag transformerar
tidskoordinaten transformerar jag även förändringsparametern. Tidskoordinaten blir då inte en
koordinat på samma sätt som rumskoordinaterna utan en storhet som måste särbehandlas.
Hur skall man kunna se tid som ett speciellt begrepp samtidigt som tidskoordinaten kan ha
rumsprojektioner? Minkowski föreslog en elegant lösning: Använd imaginär tid. Den är speciell men
blir reell när man kvadrerar den. Kvadraten kan alltså hanteras som andra koordinatkvadrater.
Ett annat sätt är att se parametertid och koordinattid som två olika begrepp.
Att se parametertid och koordinattid som olika begrepp kräver inte några nya matematiska
hjälpmedel. Det handlar bara om att hålla isär vad som är förändringsparameter och vad som är
koordinat. Och naturligtvis kan man fortfarande transformera dem som ett sammanfattande begrepp
men det viktiga är att man inte behöver göra det. Man kan transformera koordinattid som en
koordinat och parametertid som en parameter.
Den "matematik" som behövs är bara att man använder olika beteckningar för koordinattid och
parametertid. Jag brukar använda t för koordinattid och den grekiska bokstaven tao för
parametertid.
__________________
2013-03-14
Vi har alla gjort oss någon bild av den värld vi lever i. Jag tror att det kunde vara intressant att
utbyta lite erfarenheter av att använda dessa bilder. Därför berättar jag lite om min bild. Den som så
vill kan ju ibland tänka tanken: "Är detta en förändringsparameter eller en koordinat?". Kanske kan
någon se någon ny möjlighet. Bra eller dåligt? Tja det kan man ju inte säga i förväg.
Jag håller med dig om att man bör ta reda på hur den gängse världsbilden ser ut, om inte annat så
för att kunna ifrågasätta den. Och det kan också vara bra att känna till en del matematik. En vacker
dag kanske man behöver Christoffel¨s symboler eller Laplacetransformen och då kan det vara bra
att veta att de finns genomtänkta och färdiga att använda.
Naturligtvis kan man, som med Lorentztransformen, vrida x-axeln mot t-axeln så att de möts vid 45
grader bara man vet vad man gör och vet vad man skall ha resultatet till. Jag försöker bara påpeka
att det är inte det enda möjliga synsättet.
__________________